1.2: Логістичне рівняння
- Page ID
- 66649
Логістичне рівняння
Закон експоненціального зростання чисельності населення нереальний протягом тривалого часу. Зрештою, зростання буде перевірятися надмірним споживанням ресурсів. Ми припускаємо, що навколишнє середовище має внутрішню пропускну здатність\(K\), і населення, більші за цей розмір, відчувають підвищену смертність.
Для моделювання приросту населення з екологічною несучою здатністю\(K\) ми шукаємо нелінійне рівняння виду
\[\frac{d N}{d t}=r N F(N) \nonumber \]
де\(F(N)\) передбачена модель екологічного регулювання. Ця функція повинна задовольняти\(F(0)=1\) (популяція зростає в геометричній прогресії зі швидкістю зростання,\(r\) коли\(N\) невелика),\(F(K)=0\) (популяція припиняє рости при вантажопідйомності), і\(F(N)<0\) коли\(N>K\) ( популяція розпадається, коли вона більше вантажопідйомності). Найпростіша функція, яка\(F(N)\) задовольняє цим умовам, є лінійною і задається\(F(N)=1-N / K .\) результуючою моделлю відоме логістичне рівняння,
\[\frac{d N}{d t}=r N(1-N / K) \nonumber \]
важливою моделлю для багатьох процесів, крім обмеженого приросту населення.
Хоча (1.2.2) є нелінійним рівнянням, аналітичне рішення можна знайти, розділивши змінні. Перш ніж приступити до цієї алгебри, ми спочатку проілюструємо деякі основні поняття, що використовуються при аналізі нелінійних диференціальних рівнянь.
Фіксовані точки, також звані рівновагами, диференціального рівняння, такого як (1.2.2), визначаються як значення\(N\) де\(d N / d t=0\). Тут ми бачимо, що фіксовані точки (1.2.2) є\(N=0\) і\(N=K .\) Якщо початкове значення\(N\) знаходиться в одній з цих фіксованих точок, то\(N\) залишатиметься фіксованою там протягом усього часу. Фіксовані точки, однак, можуть бути стабільними або нестабільними. Фіксована точка стабільна, якщо невелике збурення від фіксованої точки спадає до нуля, так що розчин повертається до фіксованої точки. Так само фіксована точка нестабільна, якщо невелика збуреність зростає експоненціально, щоб розчин віддалявся від фіксованої точки. Розрахунок стійкості за допомогою малих збурень називається лінійним аналізом стійкості. Для прикладу розглянемо загальне одновимірне диференціальне рівняння (з використанням позначення\(\dot{x}=d x / d t\))
\[\dot{x}=f(x) \nonumber \]
з\(x_{*}\) фіксованою точкою рівняння, тобто\(f\left(x_{*}\right)=0\). Щоб аналітично визначити, чи\(x_{*}\) є стабільною або нестабільною фіксованою точкою, обурюємо рішення. Напишемо наше рішення\(x=x(t)\) у формі
\[x(t)=x_{*}+\epsilon(t) \nonumber \]
де спочатку\(\epsilon(0)\) невеликий, але відрізняється від нуля. Підставивши (1.2.4) в (1.2.3), отримуємо
\[\begin{aligned} \dot{\epsilon} &=f\left(x_{*}+\epsilon\right) \\[4pt] &=f\left(x_{*}\right)+\epsilon f^{\prime}\left(x_{*}\right)+\ldots \\[4pt] &=\epsilon f^{\prime}\left(x_{*}\right)+\ldots, \end{aligned} \nonumber \]
де друга рівність використовує розширення серії Тейлора\(f(x)\) приблизно,\(x_{*}\) а третя рівність використовує\(f\left(x_{*}\right)=0\). Якщо\(f^{\prime}\left(x_{*}\right) \neq 0\), ми можемо знехтувати термінами вищого порядку в\(\epsilon\)
для невеликих часів, і інтеграції ми маємо
\[\epsilon(t)=\epsilon(0) e^{f^{\prime}\left(x_{*}\right) t} \nonumber \]
Збурення\(\epsilon(t)\) до фіксованої точки\(x_{*}\) йде до нуля, як\(t \rightarrow \infty\) передбачено.\(f^{\prime}\left(x_{*}\right)<\)\(0 .\) Тому умова стабільності на\(x_{*}\)
\[x_{*} \text { is } \begin{cases}\text { a stable fixed point if } & f^{\prime}\left(x_{*}\right)<0, \\[4pt] \text { an unstable fixed point if } & f^{\prime}\left(x_{*}\right)>0 .\end{cases} \nonumber \]
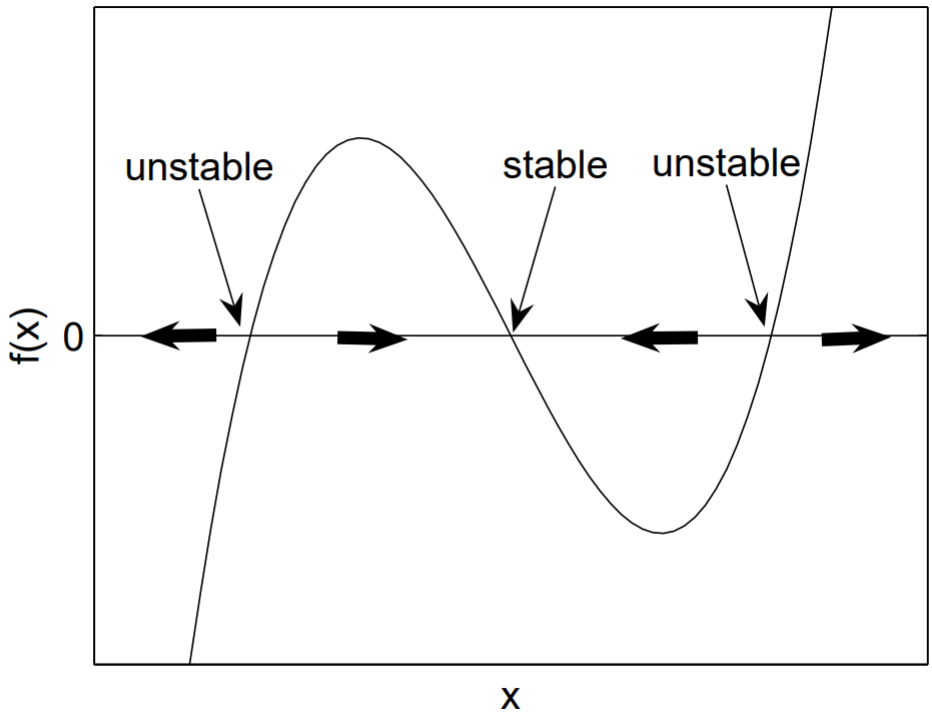
Іншим еквівалентним, але іноді простішим підходом до аналізу стійкості фіксованих точок одновимірного нелінійного рівняння, такого як (1.2.3), є побудова графіка\(f(x)\) проти\(x\). Ми показуємо загальний приклад на рис.1.1. Фіксовані точки - це\(x\) -перехоплення графіка. Спрямовані стрілки на\(x\) -осі можуть бути намальовані на основі знака\(f(x)\). Якщо\(f(x)<0\), то стрілка вказує вліво; якщо\(f(x)>0\), то стрілка вказує вправо. Стрілки показують напрямок руху для частинки в положенні, що\(x\) задовольняє\(\dot{x}=f(x)\). Як показано на рис. 1.1, нерухомі точки зі стрілками з обох сторін спрямовані в стійкі, а нерухомі точки зі стрілками з обох сторін вказують нестійкі.
У логістичному рівнянні (1.2.2) фіксованими точками\(N_{*}=0, K .\) є ескіз\(F(N)=\)\(r N(1-N / K)\) проти\(N\), з\(r, K>0\) на рис. \(1.2\)відразу показує, що\(N_{*}=0\) є нестійкою фіксованою точкою і\(N_{*}=K\) є стійкою фіксованою точкою. Аналітичний підхід обчислює\(F^{\prime}(N)=r(1-2 N / K)\), так що\(F^{\prime}(0)=r>0\) і\(F^{\prime}(K)=-r<0\). Знову робимо висновок, що\(N_{*}=0\) є\(N_{*}=K\) нестабільним і стабільним.
Тепер ми розв'язуємо логістичне рівняння аналітично. Хоча це відносно просте рівняння можна вирішити як є, ми спочатку не виміряємо, щоб проілюструвати цю дуже важливу техніку, яка згодом виявиться найбільш корисною. Можливо, тут можна вгадати відповідну одиницю часу\(1 / r\) і відповідну одиницю чисельності населення бути\(K\). Однак ми вважаємо за краще продемонструвати більш загальну техніку, яка може бути з користю застосована до рівнянь, для яких відповідні безрозмірні змінні важко здогадатися. Почнемо з нерозмірності часу та чисельності населення:
\[\tau=t / t_{*}, \quad \eta=N / N_{*} \nonumber \]
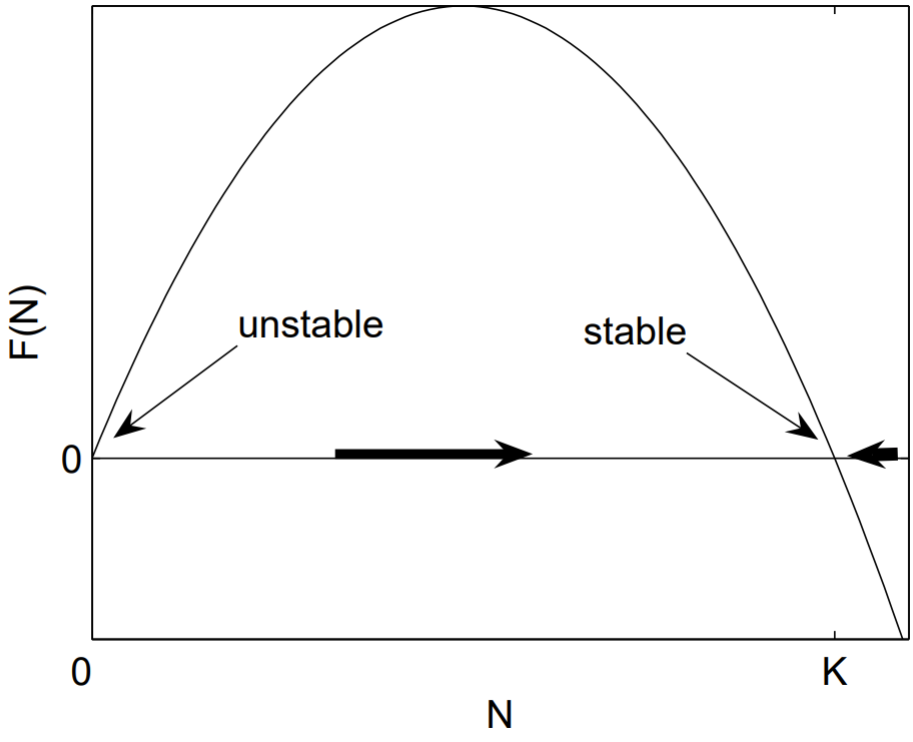
Малюнок 1.2: Визначення стійкості нерухомих точок логістичного рівняння.
де\(t_{*}\) і\(N_{*}\) є невідомими розмірними одиницями. Похідна\(N\) обчислюється як
\[\frac{d N}{d t}=\frac{d\left(N_{*} \eta\right)}{d \tau} \frac{d \tau}{d t}=\frac{N_{*}}{t_{*}} \frac{d \eta}{d \tau} \nonumber \]
Тому логістичне рівняння (1.2.2) стає
\[\frac{d \eta}{d \tau}=r t_{*} \eta\left(1-\frac{N_{*} \eta}{K}\right), \nonumber \]
який передбачає найпростішу форму з вибором\(t_{*}=1 / r\) і\(N_{*}=K\). Тому наші безрозмірні змінні
\[\tau=r t, \quad \eta=N / K \nonumber \]
і логістичне рівняння, в безрозмірному вигляді, стає
\[\frac{d \eta}{d \tau}=\eta(1-\eta) \text {, } \nonumber \]
з безрозмірною початковою умовою\(\eta(0)=\eta_{0}=N_{0} / K\), де\(N_{0}\) - початкова чисельність населення. Зверніть увагу, що безрозмірне логістичне рівняння (1.4) не має вільних параметрів, тоді як розмірна форма рівняння (1.2.2) містить\(r\) і\(K\). Зменшення кількості вільних параметрів (тут два:\(r\) і\(K\)) на кількість незалежних одиниць (тут також дві: час і чисельність населення) є загальною рисою нерозмірності. Теоретичний результат відомий як теорема Букінгемського Пі. Зменшення кількості вільних параметрів у задачі до абсолютного мінімуму особливо важливо перед тим, як приступити до числового розв'язання. Простір параметрів, який необхідно вивчити, може бути істотно зменшений.
Розв'язування безрозмірного логістичного рівняння (1.4) можна продовжити, розділивши змінні. Відокремлення та інтеграція від\(\tau=0\) до\(\tau\) та\(\eta_{0}\) до\(\eta\) врожайності
\[\int_{\eta_{0}}^{\eta} \frac{d \eta}{\eta(1-\eta)}=\int_{0}^{\tau} d \tau \nonumber \]
Інтеграл з лівого боку може бути виконаний методом часткових дробів:
\[\begin{aligned} \frac{1}{\eta(1-\eta)} &=\frac{A}{\eta}+\frac{B}{1-\eta} \\[4pt] &=\frac{A+(B-A) \eta}{\eta(1-\eta)} \end{aligned} \nonumber \]
і прирівнюючи коефіцієнти чисельників пропорційні\(\eta^{0}\) і\(\eta^{1}\), знайдемо, що\(A=1\) і\(B=1\). Тому,
\[\begin{aligned} \int_{\eta_{0}}^{\eta} \frac{d \eta}{\eta(1-\eta)} &=\int_{\eta_{0}}^{\eta} \frac{d \eta}{\eta}+\int_{\eta_{0}}^{\eta} \frac{d \eta}{(1-\eta)} \\[4pt] &=\ln \frac{\eta}{\eta_{0}}-\ln \frac{1-\eta}{1-\eta_{0}} \\[4pt] &=\ln \frac{\eta\left(1-\eta_{0}\right)}{\eta_{0}(1-\eta)} \\[4pt] &=\tau \end{aligned} \nonumber \]
Вирішуючи для\(\eta\), ми спочатку експонентіруем обидві сторони, а потім ізолюємо\(\eta:\)
\[\begin{aligned} &\frac{\eta\left(1-\eta_{0}\right)}{\eta_{0}(1-\eta)}=e^{\tau}, \text { or } \quad \eta\left(1-\eta_{0}\right)=\eta_{0} e^{\tau}-\eta \eta_{0} e^{\tau} \\[4pt] &\text { or } \eta\left(1-\eta_{0}+\eta_{0} e^{\tau}\right)=\eta_{0} e^{\tau}, \text { or } \quad \eta=\frac{\eta_{0}}{\eta_{0}+\left(1-\eta_{0}\right) e^{-\tau}} \end{aligned} \nonumber \]
Повертаючись до розмірних змінних, ми нарешті маємо
\[N(t)=\frac{N_{0}}{N_{0} / K+\left(1-N_{0} / K\right) e^{-r t}} \nonumber \]
Існує кілька способів написати кінцевий результат, який дає (1.5). Представлення математичного результату вимагає гарного естетичного почуття і є важливим елементом математичної техніки. Вирішуючи, як писати (1.5), я розглянув, чи легко спостерігати такі граничні результати: (1)\(N(0)=N_{0} ;(2) \lim _{t \rightarrow \infty} N(t)=K\); і (3)\(\lim _{K \rightarrow \infty} N(t)=N_{0} \exp (r t)\)
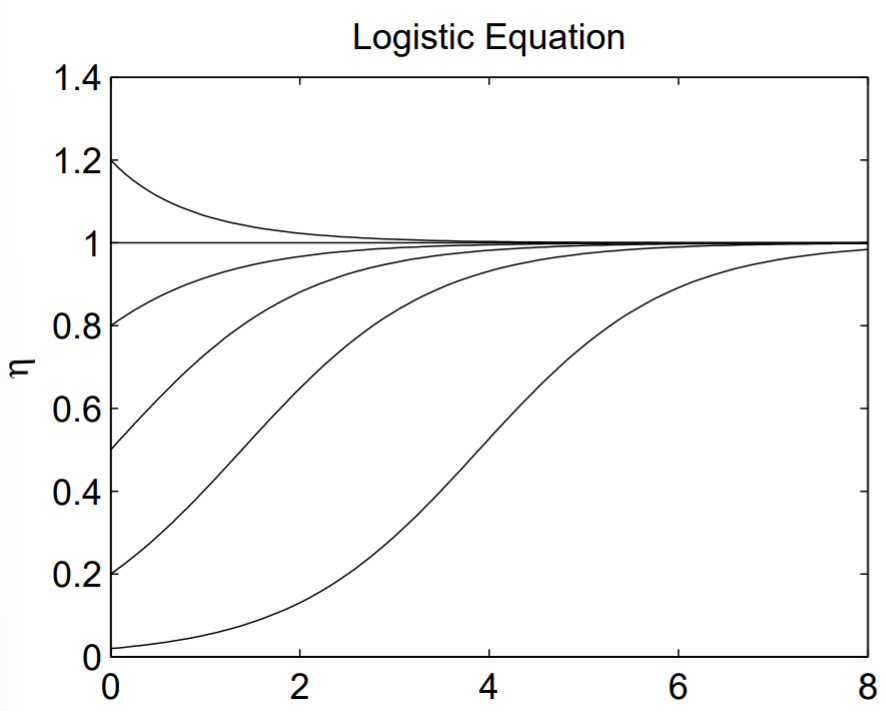
На рис. 1.3 будуємо розв'язку безрозмірного логістичного рівняння для початкових умов\(\eta_{0}=0.02,0.2,0.5,0.8,1.0\), і\(1.2\). Найнижча крива - це характеристика «S-форма», яка зазвичай асоціюється з розв'язанням логістичного рівняння. Ця сигмоїдальна крива з'являється в багатьох інших типах моделей. Сценарій MATLAB для виробництва Рис. \(1.3\)показано нижче.