15.5: Складні рекурсивні послідовності

Last updated
Save as PDF

Page ID: 66176

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Тепер ми вивчимо рекурсивно визначені послідовності комплексних чисел.

Рекурсивна послідовність

Рекурсивний зв'язок - це формула, яка пов'язує наступне значення,$z_{n+1},$ в послідовності з попереднім значенням,$z_{n} .$ Крім формули, нам потрібно початкове значення,$z_{0}$.

Послідовність отриманих значень є рекурсивною послідовністю.

Приклад 15

За заданим рекурсивним$z_{n+1}=z_{n}+2, \quad z_{0}=4,$ зв'язком генерують декілька членів
рекурсивної послідовності.

Рішення

Нам дається початкове значення,$z_{0}=4 .$ рекурсивна формула тримає для будь-якого значення$n,$ так,
якщо$n=0,$ тоді$z_{n+1}=z_{n}+2$ б сказати нам$z_{0+1}=z_{0}+2,$ або простіше,$z_{1}=z_{0}+2$

Зверніть увагу, що це визначає з$z_{1}$ точки зору відомого,$z_{0},$ щоб ми могли обчислити значення:
$ z_{1}=z_{0}+2=4+2=6 $

Тепер нехай$n=1,$ формула говорить нам$z_{1+1}=z_{1}+2,$ або$z_{2}=z_{1}+2 .$ Знову, формула дає наступне значення в послідовності через попереднє значення.

(z_ {2} =z_ {1} +2=6+2=8\)

Продовжуючи,

$z_{3}=z_{2}+2=8+2=10$

$z_{4}=z_{3}+2=10+2=12$

Попередній приклад генерував базову лінійну послідовність дійсних чисел. Цей же процес можна використовувати і з комплексними числами.

Приклад 16

За заданим рекурсивним$z_{n+1}=z_{n} \cdot i+(1-i), \quad z_{0}=4,$ зв'язком генерують декілька членів
рекурсивної послідовності.

Рішення

$z_{0}=4 .$Нас наведено за допомогою рекурсивної формули:

$z_{1}=z_{0} \cdot i+(1-i)=4 \cdot i+(1-i)=1+3 i$

$z_{2}=z_{1} \cdot i+(1-i)=(1+3 i) \cdot i+(1-i)=i+3 i^{2}+(1-i)=i-3+(1-i)=-2$

$z_{3}=z_{2} \cdot i+(1-i)=(-2) \cdot i+(1-i)=-2 i+(1-i)=1-3 i$

$z_{4}=z_{3} \cdot i+(1-i)=(1-3 i) \cdot i+(1-i)=i-3 i^{2}+(1-i)=i+3+(1-i)=4$

$z_{5}=z_{4} \cdot i+(1-i)=4 \cdot i+(1-i)=1+3 i$

Зверніть увагу, що ця послідовність демонструє цікаву закономірність — вона почала повторюватися.

Набір Мандельброта

Набір Мандельброта - це набір чисел, визначених на основі рекурсивних послідовностей

Набір Мандельброта

Для будь-якого комплексного числа$c,$ визначте послідовність$z_{n+1}=z_{n}^{2}+c, \quad z_{0}=0$

Якщо ця послідовність завжди залишається близькою до початку (в межах 2 одиниць), то число$c$ є частиною множини Мандельброта. Якщо послідовність потрапляє далеко від початку, то число не$c$ входить до складу множини.

Приклад 17

Визначте$c=1+i$, чи є частиною набору Мандельброта.

Рішення

Починаємо з$z_{0}=0$. Продовжуємо, опускаючи деякі подробиці розрахунків

$z_{1}=z_{0}^{2}+1+i=0+1+i=1+i$

$z_{2}=z_{1}^{2}+1+i=(1+i)^{2}+1+i=1+3 i$

$z_{3}=z_{2}^{2}+1+i=(1+3 i)^{2}+1+i=-7+7 i$

$z_{4}=z_{3}^{2}+1+i=(-7+7 i)^{2}+1+i=1-97 i$

Ми вже бачимо, що ці значення стають досить великими. Не здається, що$c=1+i$ є частиною набору Мандельброта.

Приклад 18

Визначте$c=0.5 i$, чи є частиною набору Мандельброта.

Рішення

Починаємо з$z_{0}=0$. Продовжуємо, опускаючи деякі подробиці розрахунків

$z_{1}=z_{0}^{2}+0.5 i=0+0.5 i=0.5 i$

$z_{2}=z_{1}^{2}+0.5 i=(0.5 i)^{2}+0.5 i=-0.25+0.5 i$

$z_{3}=z_{2}^{2}+0.5 i=(-0.25+0.5 i)^{2}+0.5 i=-0.1875+0.25 i$

$z_{4}=z_{3}^{2}+0.5 i=(-0.1875+0.25 i)^{2}+0.5 i=-0.02734+0.40625 i$

Хоча це не остаточне з цими кількома ітераціями, здається, що це значення залишається малим, припускаючи, що$0.5 i$ це частина набору Мандельброта.

Спробуйте зараз 5

Визначте$c=0.4+0.3 i$, чи є частиною набору Мандельброта.

Відповідь

$z_{1}=z_{0}^{2}+0.4+0.3 i=0+0.4+0.3 i=0.4+0.3 i$

$z_{2}=z_{1}^{2}+0.4+0.3 i=(0.4+0.3 i)^{2}+0.4+0.3 i = 0.47+0.54 i$

$z_{3}=z_{2}^{2}+0.5 i=(-0.25+0.5 i)^{2}+0.5 i=-0.1875+0.25 i$

$z_{4}=z_{3}^{2}+0.5 i=(-0.1875+0.25 i)^{2}+0.5 i=-0.02734+0.40625 i$

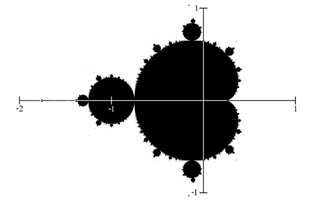$clipboard_ed4d262f8e62c4ae64b87e18c256770bc.png$ Якщо всі комплексні числа перевірені, і ми побудуємо кожне число, яке знаходиться в наборі Мандельброта на комплексній площині, отримаємо форму праворуч [1].

Кордон цієї форми проявляє квазі-самоподібність, в тому, що ділянки виглядають дуже схожими на ціле.

Крім забарвлення Мандельброта встановлює себе чорним кольором, це загальний колір точок у складній площині, що оточує безліч. Щоб створити змістовну забарвлення, часто люди підраховують кількість ітерацій рекурсивної послідовності, які потрібні для того, щоб точка отримала далі 2 одиниці від початку. Наприклад, використовуючи$c=1+i$ вище, послідовність була відстань 2 від початку після двох рекурсій.

Для деяких інших чисел може знадобитися десятки або сотні ітерацій, щоб послідовність вийшла далеко від походження. Цифри, які швидко стають великими, пофарбовані в один відтінок, тоді як кольори, які повільно ростуть, забарвлюються іншим відтінком. Наприклад, на зображенні нижче [2] світло-блакитний використовується для чисел, які швидко стають великими, тоді як темні відтінки використовуються для чисел, які ростуть повільніше. Зелень, червоні та фіолетові можна побачити, коли ми збільшуємо масштаб - вони використовуються для чисел, які ростуть дуже повільно.

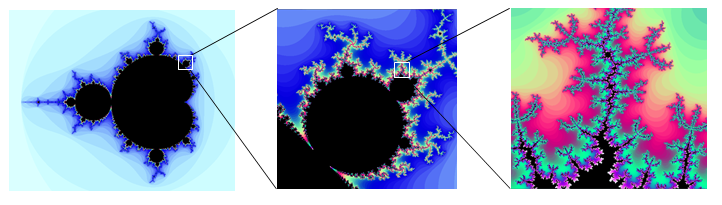
$clipboard_effebf3c2326419d73ecdad66e1b38474.png$

Набір Мандельброта, за те, що має таке просте визначення, демонструє величезну складність. Збільшення масштабу інших частин набору дає захоплюючі закручені форми.

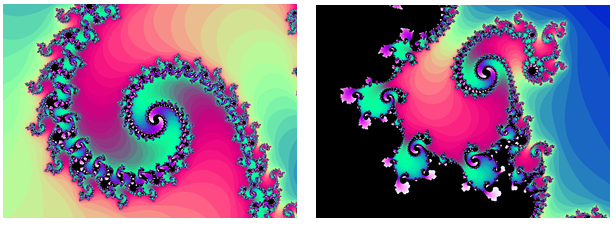
$clipboard_ef04205ce7af9e8e310324e0282465045.png$

[1] uk.wikipedia.org/wiki/Файл: Mandelset_hires.png

[2] Ця серія була створена за допомогою Scott's Mandelbrot Set Explorer