15.4: Комплексні числа

Цифри, з якими ви найбільш знайомі, називаються дійсними числами. До них відносяться такі числа, як 4, 275, -200, 10,7, ½, π тощо. Всі ці дійсні числа можуть бути нанесені на числовий рядок. Наприклад, якщо ми хотіли показати число 3, ми будуємо точку:

Для вирішення певних завдань на$x^{2}=-4$ кшталт, виникла необхідність введення уявних чисел.

Уявне число$i$

$i$Уявне число визначається бути$i=\sqrt{-1}$.

Будь-яке реальне кратне$i$$5i$, як, також є уявним числом.

Приклад 6

Спростити$\sqrt{-9}$.

Рішення

Ми можемо відокремити$\sqrt{-9}$, як$\sqrt{9} \sqrt{-1} .$ Ми можемо взяти квадратний корінь$9,$ і записати квадратний корінь -1 як$i$

$$\sqrt{-9}=\sqrt{9} \sqrt{-1}=3 i \nonumber$$

Комплексне число

Комплексне число - це число,$z=a+b i,$ де$a$ і$b$ є дійсними числами

• $a$дійсна частина комплексного числа
• $b$уявна частина комплексного числа

Для побудови комплексного числа$3-4 i$, як, нам потрібно більше, ніж просто числовий рядок, оскільки є дві складові числа. Для побудови цього числа нам знадобляться дві числові лінії, перехрещені, щоб утворити складну площину.

Складна площина

У складній площині горизонтальна вісь - це реальна вісь, а вертикальна - уявна вісь.

Приклад 7

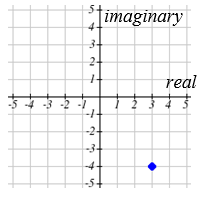
Покладіть число$3-4 i$ на складну площину.

Рішення

Реальна частина цього числа дорівнює 3, а уявна - 4. Для побудови цього малюємо точку 3 одиниці праворуч від початку в горизонтальному напрямку і 4 одиниці вниз у вертикальному напрямку.

Оскільки це аналогічно декартовій системі координат для побудови точок, ми можемо думати про побудові нашого комплексного числа$z=a+b i$ так, ніби ми будуємо точку$(a, b)$ в декартових координатах. Іноді люди пишуть складні числа,$z=x+y i$ щоб виділити це відношення.

Арифметика на комплексних числах

Перш ніж зануритися в більш складне використання складних чисел, давайте переконаємося, що ми пам'ятаємо основну арифметику, що беруть участь. Щоб скласти або відняти складні числа, ми просто додаємо подібні терміни, поєднуючи реальні частини і поєднуючи уявні частини.

Приклад 8

Додайте$3-4 i$ і$2+5 i$.

Рішення

Додавання$(3-4 i)+(2+5 i),$ ми додаємо реальні частини і уявні частини

$3+2-4 i+5 i$

$5+i$

Спробуйте зараз 3

Відняти$2+5 i$ від$3-4 i$.

Відповідь

$(3-4 i)-(2+5 i)=1-9 i$

Коли ми додаємо комплексні числа, ми можемо візуалізувати додавання як зсув, або переклад, точки в комплексній площині.

Приклад 9

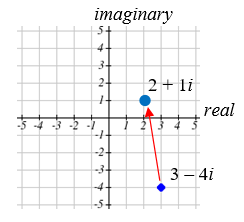
Візуалізують додавання$3-4 i$ і$-1+5 i$.

Рішення

Початкова точка є$3-4 i$. При складанні$-1+3 i$ додаємо -1 до дійсної частини, переміщаючи точку 1 одиниці вліво, і додаємо 5 до уявної частини, переміщаючи точку 5 одиниць по вертикалі. Це зміщує точку$3-4 i$ на$2+1 i$.

Ми також можемо помножити комплексні числа на дійсне число, або помножити два комплексних числа.

Приклад 10

Помножити:$4(2+5 i)$

Рішення

Щоб помножити комплексне число на дійсне число, ми просто розподіляємо так, як ми б при множенні многочленів.

$\begin{array}{ll} 4(2+5 i) & \text{Distribute} \\ =4 \cdot 2+4 \cdot 5 i & \text{Simplify} \\ =8+20 i \end{array}$

Приклад 11

Помножити:$(2+5 i)(4+i)$

Рішення

Щоб помножити комплексне число на комплексне число, ми просто розподіляємо так, як ми б при множенні многочленів.

$\begin{array}{ll} (2+5 i)(4+i) & \text{Expand} \\ =8+20 i+2 i+5 i^{2} & \text{Since }i=\sqrt{-1}, i^{2}=-1 \\ =8+20 i+2 i+5(-1) & \text{Simplify} \\ =3+22 i \end{array}$

Спробуйте зараз 4

Помножити$3-4 i$ і$2+3 i$.

Відповідь

Помножити$(3-4 i)(2+3 i)=6+9 i-8 i-12 i^{2}=6+i-12(-1)=18+i$

Щоб візуально зрозуміти ефект множення, розглянемо три приклади.

Приклад 12

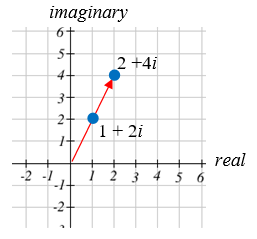Візуалізуйте продукт$2(1+2 i)$

Рішення

Множення ми отримаємо

$2 \cdot 1+2 \cdot 2 i = 2+4 i$

Зверніть увагу, як реальні, так і уявні частини були масштабовані на 2. Візуально це витягне точку назовні, подалі від початку.

Приклад 13

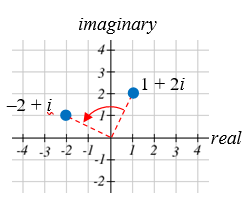Візуалізуйте продукт$i(1+2 i)$

Рішення

Помноживши, ми отримаємо

$i \cdot 1+i \cdot 2 i = i+2 i^{2}=i+2(-1)=-2+i$

При цьому відстань від початку не змінилося, але точка була повернута навколо початку, на 90° проти годинникової стрілки.

Приклад 14

Візуалізуйте результат$1+2 i$ множення на$1+i .$ Потім покажіть результат множення на$1+i$ знову.

Рішення

$1+2 i$Помножуючи на$1+i$,

$(1+2 i)(1+i)=1+i+2 i+2 i^{2}=1+3 i+2(-1)=-1+3 i$

Помножуючи на$1+i$ знову,

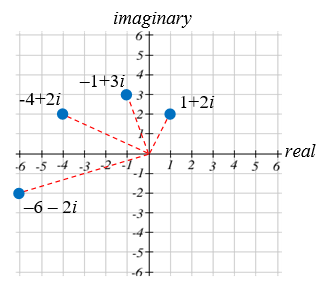
$(-1+3 i)(1+i) =-1-i+3 i+3 i^{2} =-1+2 i+3(-1) =-4+2 i$

Якщо ми помножимо на$1+i$ знову, ми отримаємо$–6–2i$. Поклавши ці числа в комплексній площині, можна помітити, що кожна точка отримує як далі від початку, так і обертається проти годинникової стрілки, в даному випадку на 45°.

Взагалі множення на комплексне число можна розглядати як масштабування, що змінює відстань від початку, поєднане з обертанням про початок.