4.2: Розширення кофактора

\(\usepackage{macros} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \)

Цілі

1. Навчіться розпізнавати, які методи найкраще підходять для обчислення визначника заданої матриці.
2. Рецепти: визначник\(3\times 3\) матриці, обчислити детермінант за допомогою кофакторних розширень.
3. Словниковий запас слів: мінор, кофактор.

У цьому розділі наведено рекурсивну формулу для детермінанти матриці, яка називається кофакторним розширенням. Формула є рекурсивною в тому, що ми обчислимо детермінант\(n\times n\) матриці, припускаючи, що ми вже знаємо, як обчислити детермінант\((n-1)\times(n-1)\) матриці.

Наприкінці наведено додатковий підрозділ про правило Крамера та формулу кофактора для оберненої матриці.

Розширення кофактора

Рекурсивна формула повинна мати початкову точку. Для кофакторних розширень відправною точкою є випадок\(1\times 1\) матриць. Визначення детермінанти безпосередньо має на увазі, що

\[ \det\left(\begin{array}{c}a\end{array}\right)=a. \nonumber \]

Для опису кофакторних розширень нам потрібно ввести деякі позначення.

Визначення\(\PageIndex{1}\): Minor and Cofactor

\(A\)Дозволяти бути\(n\times n\) матрицею.

1. \((i,j)\)Мінор,\(A_{ij}\text{,}\) позначається\((n-1)\times (n-1)\) матриця, отримана\(A\) від видалення\(i\) го рядка і\(j\) го стовпця.
2. \((i,j)\)Кофактор\(C_{ij}\) визначається з точки зору мінор по\[C_{ij}=(-1)^{i+j}\det(A_{ij}).\nonumber\]

Зверніть увагу, що ознаки кофакторів слідують «шаховому порядку». А\((-1)^{i+j}\) саме, зображено в цій матриці:

\[\left(\begin{array}{cccc}\color{Green}{+}&\color{blue}{-}&\color{Green}{+}&\color{blue}{-} \\ \color{blue}{-}&\color{Green}{+}&\color{blue}{-}&\color{Green}{-} \\ \color{Green}{+}&\color{blue}{-}&\color{Green}{+}&\color{blue}{-} \\ \color{blue}{-}&\color{Green}{+}&\color{blue}{-}&\color{Green}{+}\end{array}\right).\nonumber\]

Приклад\(\PageIndex{1}\)

Для

\[ A= \left(\begin{array}{ccc}1&2&3\\4&5&6\\7&8&9\end{array}\right), \nonumber \]

обчислювати\(A_{23}\) і\(C_{23}.\)

Рішення

Малюнок\(\PageIndex{1}\)

Кофактори\(C_{ij}\)\(n\times n\) матриці є детермінантами\((n-1)\times(n-1)\) підматриць. Звідси наступна теорема насправді є рекурсивною процедурою обчислення визначника.

Теорема\(\PageIndex{1}\): Cofactor Expansion

\(A\)Дозволяти\(n\times n\) матриця з записами\(a_{ij}\).

1. Для будь-якого\(i = 1,2,\ldots,n\text{,}\) ми маємо\[ \det(A) = \sum_{j=1}^n a_{ij}C_{ij} = a_{i1}C_{i1} + a_{i2}C_{i2} + \cdots + a_{in}C_{in}. \nonumber \] Це називається кофакторним розширенням уздовж\(i\) го ряду.
2. Для будь-якого у\(j = 1,2,\ldots,n\text{,}\) нас є\[ \det(A) = \sum_{i=1}^n a_{ij}C_{ij} = a_{1j}C_{1j} + a_{2j}C_{2j} + \cdots + a_{nj}C_{nj}. \nonumber \] Це називається кофакторним розширенням уздовж\(j\) го стовпця.

Доказ

Спочатку доведемо, що кофакторне розширення уздовж першого стовпця обчислює детермінант. Визначте функцію\(d\colon\{n\times n\text{ matrices}\}\to\mathbb{R}\) за

\[ d(A) = \sum_{i=1}^n (-1)^{i+1} a_{i1}\det(A_{i1}). \nonumber \]

Ми хочемо це показати\(d(A) = \det(A)\). Замість того, щоб показати, що\(d\) задовольняє чотирьом визначальним властивостям визначника, Визначення 4.1.1, у розділі 4.1, ми доведемо, що він задовольняє трьом альтернативним визначальним властивостям, Примітка: Альтернативні визначальні властивості, у розділі 4.1, які були показано, щоб бути еквівалентним.

1. Ми стверджуємо, що\(d\) є багатолінійним в рядах\(A\). \(A\)Дозволяти матриця з рядками\(v_1,v_2,\ldots,v_{i-1},v+w,v_{i+1},\ldots,v_n\text{:}\)\[A=\left(\begin{array}{ccc}a_11&a_12&a_13 \\ b_1+c_1 &b_2+c_2&b_3+c_3 \\ a_31&a_32&a_33\end{array}\right).\nonumber\] Тут ми дозволяємо\(b_i\) і\(c_i\) бути записи\(v\) і\(w\text{,}\) відповідно. \(B\)\(C\)Дозволяти і бути матриці з рядками\(v_1,v_2,\ldots,v_{i-1},v,v_{i+1},\ldots,v_n\) і\(v_1,v_2,\ldots,v_{i-1},w,v_{i+1},\ldots,v_n\text{,}\) відповідно:\[B=\left(\begin{array}{ccc}a_11&a_12&a_13\\b_1&b_2&b_3\\a_31&a_32&a_33\end{array}\right)\quad C=\left(\begin{array}{ccc}a_11&a_12&a_13\\c_1&c_2&c_3\\a_31&a_32&a_33\end{array}\right).\nonumber\] Ми хочемо показати\(d(A) = d(B) + d(C)\). Для\(i'\neq i\text{,}\)\((i',1)\) -кофактора\(A\) - сума\((i',1)\) -кофакторів\(B\) і\(C\text{,}\) по багатолінійності детермінант\((n-1)\times(n-1)\) матриць:\[ \begin{split} (-1)^{3+1}\det(A_{31}) \amp= (-1)^{3+1}\det\left(\begin{array}{cc}a_12&a_13\\b_2+c_2&b_3+c_3\end{array}\right) \\ \amp= (-1)^{3+1}\det\left(\begin{array}{cc}a_12&a_13\\b_2&b_3\end{array}\right) + (-1)^{3+1}\det\left(\begin{array}{cc}a_12&a_13\\c_2&c_3\end{array}\right) \\ \amp= (-1)^{3+1}\det(B_{31}) + (-1)^{3+1}\det(C_{31}). \end{split} \nonumber \] З іншого боку,\((i,1)\) -кофактори\(A,B,\) і\(C\) всі однакові: \[ \begin{split} (-1)^{2+1} \det(A_{21}) \amp= (-1)^{2+1} \det\left(\begin{array}{cc}a_12&a_13\\a_32&a_33\end{array}\right) \\ \amp= (-1)^{2+1} \det(B_{21}) = (-1)^{2+1} \det(C_{21}). \end{split} \nonumber \]Тепер обчислюємо за\[ \begin{split} d(A) \amp= (-1)^{i+1} (b_i + c_i)\det(A_{i1}) + \sum_{i'\neq i} (-1)^{i'+1} a_{i1}\det(A_{i'1}) \\ \amp= (-1)^{i+1} b_i\det(B_{i1}) + (-1)^{i+1} c_i\det(C_{i1}) \\ \amp\qquad\qquad+ \sum_{i'\neq i} (-1)^{i'+1} a_{i1}\bigl(\det(B_{i'1}) + \det(C_{i'1})\bigr) \\ \amp= \left[(-1)^{i+1} b_i\det(B_{i1}) + \sum_{i'\neq i} (-1)^{i'+1} a_{i1}\det(B_{i'1})\right] \\ \amp\qquad\qquad+ \left[(-1)^{i+1} c_i\det(C_{i1}) + \sum_{i'\neq i} (-1)^{i'+1} a_{i1}\det(C_{i'1})\right] \\ \amp= d(B) + d(C), \end{split} \nonumber \] бажанням. Це показує, що\(d(A)\) задовольняє першу визначальну властивість у рядках\(A\).
   Ми ще повинні показати, що\(d(A)\) задовольняє друге визначальне властивість в рядках\(A\). \(B\)Дозволяти матриця, отримана\(A\) масштабуванням\(i\) го рядка на коефіцієнт\(c\text{:}\)
   \[A=\left(\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{array}\right)\quad B=\left(\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\ca_{21}&ca_{22}&ca_{23}\\a_{31}&a_{32}&a_{33}\end{array}\right).\nonumber\] Ми хочемо показати, що\(d(B) = c\,d(A)\). Для\(i'\neq i\text{,}\)\((i',1)\) -кофактора з\(B\)\(c\) разів\((i',1)\) -кофактор багатолінійності детермінант\((n-1)\times(n-1)\) -матриць:\[ \begin{split} (-1)^{3+1}\det(B_{31}) \amp= (-1)^{3+1}\det\left(\begin{array}{cc}a_{12}&a_{13}\\ca_{22}&ca_{23}\end{array}\right) \\ \amp= (-1)^{3+1}\cdot c\det\left(\begin{array}{cc}a_{12}&a_{13}\\a_{22}&a_{23}\end{array}\right) = (-1)^{3+1}\cdot c\det(A_{31}). \end{split} \nonumber \] З іншого боку,\((i,1)\) -кофактори\(A\) і\(B\) однакові:\[ (-1)^{2+1} \det(B_{21}) = (-1)^{2+1} \det\left(\begin{array}{cc}a_{12}&a_{13}\\a_{32}&a_{33}\end{array}\right) = (-1)^{2+1} \det(A_{21}). \nonumber \] Тепер ми\(A\text{,}\) обчислити за\[ \begin{split} d(B) \amp= (-1)^{i+1}ca_{i1}\det(B_{i1}) + \sum_{i'\neq i}(-1)^{i'+1} a_{i'1}\det(B_{i'1}) \\ \amp= (-1)^{i+1}ca_{i1}\det(A_{i1}) + \sum_{i'\neq i}(-1)^{i'+1} a_{i'1}\cdot c\det(A_{i'1}) \\ \amp= c\left[(-1)^{i+1}ca_{i1}\det(A_{i1}) + \sum_{i'\neq i}(-1)^{i'+1} a_{i'1} \det(A_{i'1})\right] \\ \amp= c\,d(A), \end{split} \nonumber \] бажанням. На цьому доказ того, що\(d(A)\) є багатолінійним в рядах\(A\).
2. Тепер ми покажемо, що\(d(A) = 0\) якщо\(A\) має два однакових рядки. Припустимо, що рядки\(i_1,i_2\)\(A\) однакові, з\(i_1 \lt i_2\text{:}\)\[A=\left(\begin{array}{cccc}a_{11}&a_{12}&a_{13}&a_{14}\\a_{21}&a_{22}&a_{23}&a_{24}\\a_{31}&a_{32}&a_{33}&a_{34}\\a_{11}&a_{12}&a_{13}&a_{14}\end{array}\right).\nonumber\] If\(i\neq i_1,i_2\) тоді\((i,1)\) -кофактор\(A\) дорівнює нулю, оскільки\(A_{i1}\) є\((n-1)\times(n-1)\) матрицею з однаковими рядками:\[ (-1)^{2+1}\det(A_{21}) = (-1)^{2+1} \det\left(\begin{array}{ccc}a_{12}&a_{13}&a_{14}\\a_{32}&a_{33}&a_{34}\\a_{12}&a_{13}&a_{14}\end{array}\right) = 0. \nonumber \]\((i_1,1)\) -мінор може бути перетворений в\((i_2,1)\) - незначні за допомогою свопів\(i_2 - i_1 - 1\) рядків:

Малюнок\(\PageIndex{2}\)

2. Тому два інші кофактори\[ (-1)^{i_1+1}\det(A_{i_11}) = (-1)^{i_1+1}\cdot(-1)^{i_2 - i_1 - 1}\det(A_{i_21}) = -(-1)^{i_2+1}\det(A_{i_21}). \nonumber \] скасовують,\(d(A) = 0\text{,}\) так за бажанням.
3. Залишилося це показати\(d(I_n) = 1\). Перший є єдиним ненульовим терміном у кофакторному розширенні ідентичності:\[ d(I_n) = 1\cdot(-1)^{1+1}\det(I_{n-1}) = 1. \nonumber \]

Це доводить, що\(\det(A) = d(A)\text{,}\) тобто, що кофакторне розширення вздовж першого стовпця обчислює детермінант.

Тепер покажемо, що кофакторне\(j\) розширення уздовж колонки також обчислює детермінант. Виконуючи свопи\(j-1\) стовпців, можна перемістити\(j\) й стовпець матриці до першого стовпця, зберігаючи порядок інших стовпців. Наприклад, тут ми переміщаємо третій стовпець до першого, використовуючи два підкачки стовпців:

Малюнок\(\PageIndex{3}\)

\(B\)Дозволяти матриця, отримана при переміщенні\(j\) го стовпця\(A\) до першого стовпця таким чином. Тоді\((i,j)\) неповнолітній\(A_{ij}\) дорівнює\((i,1)\) неповнолітньому,\(B_{i1}\text{,}\) оскільки видалення\(i\) го стовпця\(A\) - це те саме, що видалення першого стовпця\(B\). За конструкцією\((i,j)\)\(a_{ij}\) -entry\(A\) дорівнює\((i,1)\) -entry\(b_{i1}\) of\(B\). Оскільки ми знаємо, що ми можемо обчислити детермінанти, розширюючи вздовж першого стовпця, ми маємо

\[ \det(B) = \sum_{i=1}^n (-1)^{i+1} b_{i1}\det(B_{i1}) = \sum_{i=1}^n (-1)^{i+1} a_{ij}\det(A_{ij}). \nonumber \]

Так як\(B\) був\(A\) отриманий від виконання свапів\(j-1\) стовпців, у нас є

\[ \begin{split} \det(A) = (-1)^{j-1}\det(B) \amp= (-1)^{j-1}\sum_{i=1}^n (-1)^{i+1} a_{ij}\det(A_{ij}) \\ \amp= \sum_{i=1}^n (-1)^{i+j} a_{ij}\det(A_{ij}). \end{split} \nonumber \]

Це доводить, що кофакторне\(i\) розширення уздовж колони обчислює детермінант\(A\).

За властивістю транспонування, Пропозиція 4.1.4 в Розділі 4.1, розширення кофактора уздовж\(i\) го ряду\(A\) таке ж, як розширення кофактора\(i\) вздовж колони\(A^T\). Знову за властивістю транспонування, у нас є\(\det(A)=\det(A^T)\text{,}\) так розширюються кофактори уздовж ряду також обчислює детермінант.

Зауважте, що теорема насправді дає\(2n\) різні формули для визначника: по одній для кожного рядка і по одній для кожного стовпця. Наприклад, формула для розширення кофактора вздовж першого стовпця

\[ \begin{split} \det(A) = \sum_{i=1}^n a_{i1}C_{i1} \amp= a_{11}C_{11} + a_{21}C_{21} + \cdots + a_{n1}C_{n1} \\ \amp= a_{11}\det(A_{11}) - a_{21}\det(A_{21}) + a_{31}\det(A_{31}) - \cdots \pm a_{n1}\det(A_{n1}). \end{split} \nonumber \]

Пам'ятайте, що детермінант матриці - це лише число, визначене чотирма визначальними властивостями, Визначенням 4.1.1 в Розділі 4.1, щоб бути зрозумілим:

Примітка\(\PageIndex{1}\)

Ви отримуєте таке ж число, розширюючи кофактори вздовж\(any\) рядка або стовпця.

Тепер, коли ми маємо рекурсивну формулу для детермінанти, ми можемо остаточно довести теорему існування, Теорема 4.1.1 в розділі 4.1.

Доказ

Давайте розглянемо, що ми насправді довели в розділі 4.1. Ми показали, що якщо будь-яка функція\(\det\colon\{n\times n\text{ matrices}\}\to\mathbb{R}\) задовольняє чотири визначальні властивості детермінанта, визначення 4.1.1 у розділі 4.1 (або три альтернативні визначальні властивості, Зауваження: Альтернативні визначальні властивості), то вона також задовольняє всі чудові властивості доведено в цьому розділі. Зокрема, оскільки\(\det\) можна обчислити за допомогою скорочення рядків за допомогою Recipe: Computing Determinants by Row Reduction, він однозначно характеризується визначальними властивостями. Те, що ми не довели, було існування такої функції, оскільки ми не знали, що дві різні процедури скорочення рядків завжди обчислюватимуть одну і ту ж відповідь.

Розглянемо функцію,\(d\) визначену кофакторним розширенням уздовж першого ряду:

\[ d(A) = \sum_{i=1}^n (-1)^{i+1} a_{i1}\det(A_{i1}). \nonumber \]

Якщо припустити, що детермінант існує для\((n-1)\times(n-1)\) матриць, то немає сумніву, що функція\(d\) існує, так як ми дали для неї формулу. Більше того, ми показали в доведенні теореми\(\PageIndex{1}\) вище, що\(d\) задовольняє три альтернативні визначальні властивості детермінанти, знову ж таки лише припускаючи, що детермінант існує для\((n-1)\times(n-1)\) матриць. Це доводить існування детермінанти для\(n\times n\) матриць!

Це приклад доказу шляхом математичної індукції. Почнемо з того, що помічаємо, що\(\det\left(\begin{array}{c}a\end{array}\right) = a\) задовольняє чотири визначальні властивості детермінанти\(1\times 1\) матриці. Потім ми показали, що детермінант\(n\times n\) матриць існує, припускаючи, що детермінант\((n-1)\times(n-1)\) матриць існує. Це означає, що всі детермінанти існують, за наступним ланцюжком логіки:

\[ 1\times 1\text{ exists} \;\implies\; 2\times 2\text{ exists} \;\implies\; 3\times 3\text{ exists} \;\implies\; \cdots. \nonumber \]

Приклад\(\PageIndex{2}\)

Знайдіть детермінант

\[ A= \left(\begin{array}{ccc}2&1&3\\-1&2&1\\-2&2&3\end{array}\right). \nonumber \]

Рішення

Робимо кілька довільний вибір для розширення уздовж першого ряду. Неповнолітніми та кофакторами є

Малюнок\(\PageIndex{4}\)

Таким чином,

\[ \det(A)=a_{11}C_{11}+a_{12}C_{12}+a_{13}C_{13} =(2)(4)+(1)(1)+(3)(2)=15. \nonumber \]

Приклад\(\PageIndex{3}\): The Determinant of a \(2\times 2\) Matrix

Обчислимо (знову) детермінант загальної\(2\times2\) матриці

\[ A=\left(\begin{array}{cc}a&b\\c&d\end{array}\right). \nonumber \]

Неповнолітні

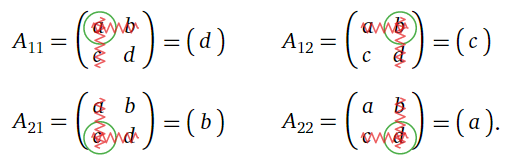
Малюнок\(\PageIndex{5}\)

Неповнолітні - це всі\(1\times 1\) матриці. Як ми бачили, що детермінант\(1\times1\) матриці - це лише число всередині неї, тому кофактори

\ почати {вирівнювати*} C_ {11} &= {+\ det (A_ {11}) = д} & C_ {12} &= {-\ det (A_ {12}) = -c}\\ C_ {21} &= {-\ det (A_ {21}) = -б} & C_ {22} &= {+\ det (A_ {22}) = a}\ end {вирівнювати*}

Розширюючи кофактори уздовж першої колонки, ми виявляємо, що

\[ \det(A)=aC_{11}+cC_{21} = ad - bc, \nonumber \]

який узгоджується з формулами у Визначенні 3.5.2 у розділі 3.5 та прикладі 4.1.6 у розділі 4.1.

Приклад\(\PageIndex{4}\): The Determinant of a \(3\times 3\) Matrix

Ми також можемо використовувати кофакторні розширення, щоб знайти формулу детермінанти\(3\times 3\) матриці. Дозвольте обчислити детермінант

\[ A = \left(\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{array}\right) \nonumber \]

шляхом розширення уздовж першого ряду. Неповнолітніми та кофакторами є:

Малюнок\(\PageIndex{6}\)

Детермінантом є:

\ begin {вирівнювати*}\ det (A)\ amp= a_ {11} C_ {11} + a_ {12} C_ {12} + a_ {13} C_ {13}\\ amp= a_ {11}\ det\ left (\ begin {масив} {cc} a_ {22} &a_ {23}\ a_ {32} &a_ {33} кінець {масив}\ праворуч) - a_ {12}\ det\ left (\ begin {масив} {cc} a_ {21} &a_ {23}\ a_ {31} &a_ {33}\ кінець {масив}\ справа) + a_ {13}\ det\ left (\ begin {масив} {cc} a_ {21} &a_ {22}\ a_ {31} &a_ {32}\ кінець {масив}\ право)\\\ amp= a_ {11} (a_ {22} a_ {33} -a_ {23} a_ {32}) - a_ {12} (a_ {21} a_ {33} -a_ {23} a_ {31}) + a_ {13} (a_ {21} a_ {21} a_ {21} a_ {31} 32} -a_ {22} a_ {31})\\ амп= a_ {11} a_ {22} a_ {33} + a_ {12} a_ {23} a_ {31} + a_ {13} a_ {21} a_ {32} -a_ {13} a_ {22} a_ {31} - a_ {11} a_ {23} _ {32} - a_ {12} a_ {21} a_ {33}. \ end {вирівнювати*}

Формула для детермінанти\(3\times 3\) матриці виглядає занадто складною для повного запам'ятовування. На щастя, існує наступне мнемонічний пристрій.

Рецепт: Обчислення детермінанта\(3\times 3\) Matrix

Щоб обчислити детермінант\(3\times 3\) матриці, спочатку намалюйте більшу матрицю з першими двома стовпцями, повтореними праворуч. Потім складіть вироби низхідних діагоналей разом, і відніміть вироби висхідних діагоналей:

\[\det\left(\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{array}\right)=\begin{array}{l} \color{Green}{a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}} \\ \color{blue}{\quad -a_{13}a_{22}a_{31}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}}\end{array} \nonumber\]

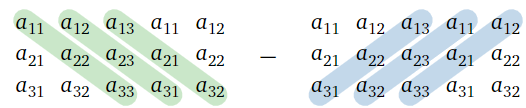
Малюнок\(\PageIndex{7}\)

Як варіант, не варто повторювати перші два стовпці, якщо ви дозволяєте своїм діагоналям «обертати» сторони матриці, як у Pac-Man або Asteroids.

Приклад\(\PageIndex{5}\)

Знайдіть детермінант\(A=\left(\begin{array}{ccc}1&3&5\\2&0&-1\\4&-3&1\end{array}\right)\).

Рішення

Повторюємо перші два стовпчики справа, потім складаємо вироби низхідних діагоналей і віднімаємо вироби висхідних діагоналей:

Малюнок\(\PageIndex{8}\)

\[\det\left(\begin{array}{ccc}1&3&5\\2&0&-1\\4&-3&1\end{array}\right)=\begin{array}{l}\color{Green}{(1)(0)(1)+(3)(-1)(4)+(5)(2)(-3)} \\ \color{blue}{\quad -(5)(0)(4)-(1)(-1)(-3)-(3)(2)(1)}\end{array} =-51.\nonumber\]

Розширення кофактора найбільш корисні при обчисленні визначника матриці, яка має рядок або стовпець з декількома нульовими записами. Дійсно, якщо\((i,j)\) запис\(A\) дорівнює нулю, то немає підстав обчислювати\((i,j)\) кофактор. У наступному прикладі ми обчислюємо детермінант матриці з двома нулями в четвертому стовпці шляхом розширення кофакторів вздовж четвертого стовпця.

Приклад\(\PageIndex{6}\)

Знайдіть детермінант

\[ A= \left(\begin{array}{cccc}2&5&-3&-2\\-2&-3&2&-5\\1&3&-2&0\\-1&6&4&0\end{array}\right). \nonumber \]

Рішення

Четвертий стовпець має два нульові записи. Розгортаємо уздовж четвертої колони, щоб знайти

\[ \begin{split} \det(A) \amp= 2\det\left(\begin{array}{ccc}-2&-3&2\\1&3&-2\\-1&6&4\end{array}\right) -5 \det \left(\begin{array}{ccc}2&5&-3\\1&3&-2\\-1&6&4\end{array}\right) \\ \amp\qquad - 0\det(\text{don't care}) + 0\det(\text{don't care}). \end{split} \nonumber \]

Нам залишається лише обчислити два кофактора. Ми можемо знайти ці детермінанти будь-яким методом, який ми бажаємо; для ілюстрації ми розширимо кофактори на одному і використаємо формулу для\(3\times 3\) детермінанти на іншому.

Розгортаючи уздовж першого стовпця, обчислюємо

\ begin {align*} &\ det\ left (\ begin {масив} {ccc} -2&-3&2\\ 1&-2\ -1&6&4\ кінець {масив}\ справа)\\ &\ quad= -2\ det\ left (\\ begin {масив} {cc} 3&2\ 6&4\ кінець {масив}\ праворуч) -\ det\ left\ почати {масив} {cc} -3&2\\ 6&4\ end {масив}\ праворуч) -\ det\ left (\ begin {масив} {cc} -3&2\\ 3&-2\ кінець {масив}\ праворуч)\\ &\ quad= -2 (24) - (-24) -0 = -48+24+0=-24. \ end {вирівнювати*}

Використовуючи формулу для\(3\times 3\) детермінанти, ми маємо

\[\det\left(\begin{array}{ccc}2&5&-3\\1&3&-2\\-1&6&4\end{array}\right)=\begin{array}{l}\color{Green}{(2)(3)(4) + (5)(-2)(-1)+(-3)(1)(6)} \\ \color{blue}{\quad -(2)(-2)(6)-(5)(1)(4)-(-3)(3)(-1)}\end{array} =11.\nonumber\]

Таким чином, ми виявляємо, що

\[ \det(A)= 2(-24)-5(11)=-103. \nonumber \]

Розширення кофактора також дуже корисні при обчисленні детермінанта матриці з невідомими записами. Дійсно, в цьому випадку незручно скорочувати рядки, тому що не можна бути впевненим, чи є запис, що містить невідоме, є стрижнем чи ні.

Приклад\(\PageIndex{7}\)

Обчислити детермінант цієї матриці, що містить невідоме\(\lambda\text{:}\)

\[A=\left(\begin{array}{cccc}-\lambda&2&7&12\\3&1-\lambda&2&-4\\0&1&-\lambda&7\\0&0&0&2-\lambda\end{array}\right).\nonumber\]

Рішення

Спочатку розгортаємо кофактори уздовж четвертого ряду:

\[ \begin{split} \det(A) \amp= 0\det\left(\begin{array}{c}\cdots\end{array}\right) + 0\det\left(\begin{array}{c}\cdots\end{array}\right) + 0\det\left(\begin{array}{c}\cdots\end{array}\right) \\ \amp\qquad+ (2-\lambda)\det\left(\begin{array}{ccc}-\lambda&2&7\\3&1-\lambda &2\\0&1&-\lambda\end{array}\right). \end{split} \nonumber \]

Нам залишається лише обчислити один кофактор. Для цього спочатку ми очищаємо\((3,3)\) -запис, виконавши заміну стовпця,\(C_3 = C_3 + \lambda C_2\text{,}\) яка не змінює детермінант:

\[ \det\left(\begin{array}{ccc}-\lambda&2&7\\3&1-\lambda &2\\0&1&-\lambda\end{array}\right) = \det\left(\begin{array}{ccc}-\lambda&2&7+2\lambda \\ 3&1-\lambda&2+\lambda(1-\lambda) \\ 0&1&0\end{array}\right). \nonumber \]

Тепер розгортаємо кофактори уздовж третього ряду, щоб знайти

\[ \begin{split} \det\left(\begin{array}{ccc}-\lambda&2&7+2\lambda \\ 3&1-\lambda&2+\lambda(1-\lambda) \\ 0&1&0\end{array}\right) \amp= (-1)^{2+3}\det\left(\begin{array}{cc}-\lambda&7+2\lambda \\ 3&2+\lambda(1-\lambda)\end{array}\right) \\ \amp= -\biggl(-\lambda\bigl(2+\lambda(1-\lambda)\bigr) - 3(7+2\lambda) \biggr) \\ \amp= -\lambda^3 + \lambda^2 + 8\lambda + 21. \end{split} \nonumber \]

Тому у нас є

\[ \det(A) = (2-\lambda)(-\lambda^3 + \lambda^2 + 8\lambda + 21) = \lambda^4 - 3\lambda^3 - 6\lambda^2 - 5\lambda + 42. \nonumber \]

Часто найбільш ефективно використовувати комбінацію декількох прийомів при обчисленні детермінанта матриці. Дійсно, при розширенні кофакторів на матриці можна обчислити детермінанти кофакторів будь-яким зручним способом. Або можна виконати операції з рядками та стовпцями, щоб очистити деякі записи матриці перед розширенням кофакторів, як у попередньому прикладі.

Примітка\(\PageIndex{2}\): Summary: Methods for Computing Determinants

У нас є кілька способів обчислення детермінант:

1. Спеціальні формули для\(2\times 2\) і\(3\times 3\) матриць.
   Зазвичай це найкращий спосіб обчислити детермінант малої матриці, за винятком матриці з декількома нульовими записами.\(3\times 3\)
2. Розширення кофактора.
   Зазвичай це найбільш ефективно, коли є рядок або стовпець з декількома нульовими записами, або якщо матриця має невідомі записи.
3. Операції з рядками та стовпцями.
   Це, як правило, найшвидший, коли представлений великою матрицею, яка не має рядка або стовпця з великою кількістю нулів у ньому.
4. Будь-яка комбінація з перерахованих вище.
   Розширення кофактора є рекурсивним, але можна обчислити детермінанти неповнолітніх, використовуючи будь-який спосіб, який є найбільш зручним. Або ви можете виконати операції з рядками та стовпцями, щоб очистити деякі записи матриці перед розширенням кофакторів.

Пам'ятайте, всі методи обчислення детермінанта дають одне і те ж число.

Правило Крамера і матричні зворотні

Нагадаємо з Пропозиції 3.5.1 в розділі 3.5, що можна обчислити детермінант\(2\times 2\) матриці за допомогою правила

\[ A = \left(\begin{array}{cc}d&-b\\-c&a\end{array}\right) \quad\implies\quad A^{-1} = \frac 1{\det(A)}\left(\begin{array}{cc}d&-b\\-c&a\end{array}\right). \nonumber \]

Ми обчислили кофактори\(2\times 2\) матриці в прикладі\(\PageIndex{3}\); використовуючи\(C_{11}=d,\,C_{12}=-c,\,C_{21}=-b,\,C_{22}=a\text{,}\) ми можемо переписати вищевказану формулу як

\[ A^{-1} = \frac 1{\det(A)}\left(\begin{array}{cc}C_{11}&C_{21}\\C_{12}&C_{22}\end{array}\right). \nonumber \]

Виходить, що ця формула узагальнюється до\(n\times n\) матриць.

Теорема\(\PageIndex{2}\)

\(A\)Дозволяти бути оборотна\(n\times n\) матриця, з кофакторами\(C_{ij}\). Тоді

\[\label{eq:1}A^{-1}=\frac{1}{\det (A)}\left(\begin{array}{ccccc}C_{11}&C_{21}&\cdots&C_{n-1,1}&C_{n1} \\ C_{12}&C_{22}&\cdots &C_{n-1,2}&C_{n2} \\ \vdots&\vdots &\ddots&\vdots&\vdots \\ C_{1,n-1}&C_{2,n-1}&\cdots &C_{n-1,n-1}&C_{n,n-1} \\ C_{1n}&C_{2n}&\cdots &C_{n-1,n}&C_{nn}\end{array}\right).\]

Матрицю кофакторів іноді називають регулюючою матрицею\(A\text{,}\) і позначається\(\text{adj}(A)\text{:}\)

\[\text{adj}(A)=\left(\begin{array}{ccccc}C_{11}&C_{21}&\cdots &C_{n-1,1}&C_{n1} \\ C_{12}&C_{22}&\cdots &C_{n-1,2}&C_{n2} \\ \vdots&\vdots&\ddots&\vdots&\vdots \\ C_{1,n-1}&C_{2,n-1}&\cdots &C_{n-1,n-1}&C_{n,n-1} \\ C_{1n}&C_{2n}&\cdots &C_{n-1,n}&C_{nn}\end{array}\right).\nonumber\]

Зверніть увагу, що\((i,j)\) кофактор\(C_{ij}\) переходить у\((j,i)\) запис матрицю регулювання, а не\((i,j)\) запис: матриця adjugate - це транспонування матриці кофактора.

Зауваження

Насправді завжди є,\(A\cdot\text{adj}(A) = \text{adj}(A)\cdot A = \det(A)I_n,\) чи є\(A\) оборотним чи ні.

Приклад\(\PageIndex{8}\)

Використовуйте теорему,\(\PageIndex{2}\) щоб обчислити\(A^{-1}\text{,}\), де

\[ A = \left(\begin{array}{ccc}1&0&1\\0&1&1\\1&1&0\end{array}\right). \nonumber \]

Рішення

Неповнолітніми є:

\[\begin{array}{lllll}A_{11}=\left(\begin{array}{cc}1&1\\1&0\end{array}\right)&\quad&A_{12}=\left(\begin{array}{cc}0&1\\1&0\end{array}\right)&\quad&A_{13}=\left(\begin{array}{cc}0&1\\1&1\end{array}\right) \\ A_{21}=\left(\begin{array}{cc}0&1\\1&0\end{array}\right)&\quad&A_{22}=\left(\begin{array}{cc}1&1\\1&0\end{array}\right)&\quad&A_{23}=\left(\begin{array}{cc}1&0\\1&1\end{array}\right) \\ A_{31}=\left(\begin{array}{cc}0&1\\1&1\end{array}\right)&\quad&A_{32}=\left(\begin{array}{cc}1&1\\0&1\end{array}\right)&\quad&A_{33}=\left(\begin{array}{cc}1&0\\0&1\end{array}\right)\end{array}\nonumber\]

Кофакторами є:

\[\begin{array}{lllll}C_{11}=-1&\quad&C_{12}=1&\quad&C_{13}=-1 \\ C_{21}=1&\quad&C_{22}=-1&\quad&C_{23}=-1 \\ C_{31}=-1&\quad&C_{32}=-1&\quad&C_{33}=1\end{array}\nonumber\]

Розгортаючи уздовж першого ряду, обчислюємо детермінант бути

\[ \det(A) = 1\cdot C_{11} + 0\cdot C_{12} + 1\cdot C_{13} = -2. \nonumber \]

Тому зворотним є

\[ A^{-1} = \frac 1{\det(A)} \left(\begin{array}{ccc}C_{11}&C_{21}&C_{31}\\C_{12}&C_{22}&C_{32}\\C_{13}&C_{23}&C_{33}\end{array}\right) = -\frac12\left(\begin{array}{ccc}-1&1&-1\\1&-1&-1\\-1&-1&1\end{array}\right). \nonumber \]

З попереднього прикладу зрозуміло, що\(\eqref{eq:1}\) це дуже неефективний спосіб обчислення зворотної матриці, порівняно з доповненням матрицею ідентичності та зменшенням рядків, як у підрозділі Обчислення зворотної матриці в розділі 3.5. Однак він має своє застосування.

• Якщо матриця має невідомі записи, то важко обчислити її зворотну за допомогою скорочення рядків, з тієї ж причини важко обчислити визначник таким чином: не можна бути впевненим, чи є запис, що містить невідоме, є стрижнем чи ні.
• Ця формула стане в нагоді в теоретичних цілях. Зверніть увагу, що єдині знаменники\(\eqref{eq:1}\) виникають при діленні на детермінант: обчислювальні кофактори включають лише множення та додавання, а не ділення. Це означає, наприклад, що якщо детермінант дуже малий, то будь-яка похибка вимірювання в записах матриці значно збільшується при обчисленні зворотного. Таким чином,\(\eqref{eq:1}\) корисний при аналізі помилок.

Доказ теореми\(\PageIndex{2}\) використовує цікавий трюк під назвою Правило Крамера, який дає формулу для записів розв'язку оборотного матричного рівняння.

Теорема\(\PageIndex{3}\): Cramer's Rule

\(x = (x_1,x_2,\ldots,x_n)\)Дозволяти бути розв'язком\(Ax=b\text{,}\) де\(A\) є оборотна\(n\times n\) матриця і\(b\) є вектором в\(\mathbb{R}^n \). \(A_i\)Дозволяти матриця, отримана\(A\) від заміни\(i\) го стовпця на\(b\). Тоді

\[ x_i = \frac{\det(A_i)}{\det(A)}. \nonumber \]

Доказ

Спочатку припустимо, що\(A\) це матриця ідентичності, так що\(x = b\). Тоді матриця\(A_i\) виглядає так:

\[ \left(\begin{array}{cccc}1&0&b_1&0\\0&1&b_2&0\\0&0&b_3&0\\0&0&b_4&1\end{array}\right). \nonumber \]

Розширюючи кофактори уздовж\(i\) -го ряду, ми бачимо, що\(\det(A_i)=b_i\text{,}\) так в даному випадку

\[ x_i = b_i = \det(A_i) = \frac{\det(A_i)}{\det(A)}. \nonumber \]

Тепер нехай\(A\) буде загальна\(n\times n\) матриця. Один із способів вирішення\(Ax=b\) полягає у зменшенні рядка розширеної\((\,A\mid b\,)\text{;}\) матриці результат. У випадку, який ми розглядали вище, достатньо перевірити, чи кількість\(\det(A_i)/\det(A)\) не змінюється, коли ми робимо операцію рядка до того\((\,A\mid b\,)\text{,}\) моменту,\(\det(A_i)/\det(A) = x_i\) коли\(A = I_n\).\((\,I_n\mid x\,).\)

1. Виконання заміни рядка на\((\,A\mid b\,)\) робить ту саму заміну рядка на\(A\) і на\(A_i\text{:}\)
   \[\begin{aligned}\left(\begin{array}{ccc|c}a_{11}&a_{12}&a_{13}&b_1 \\ a_{21}&a_{22}&a_{23}&b_2\\a_{31}&a_{32}&a_{33}&b_3\end{array}\right)\quad\xrightarrow{R_2=R_2-2R_3}\quad&\left(\begin{array}{lll|l}a_{11}&a_{12}&a_{13}&b_1\\ a_{21}-2a_{31}&a_{22}-2a_{32}&a_{23}-2a_{33}&b_2-2b_3 \\ a_{31}&a_{32}&a_{33}&b_3 \end{array}\right) \\ \left(\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{array}\right)\quad \xrightarrow{R_2=R_2-2R_3}\quad&\left(\begin{array}{ccc}a_{11}&a_{12}&a_{13} \\ a_{21}-2a_{31}&a_{22}-2a_{32}&a_{23}-2a_{33} \\ a_{31}&a_{32}&a_{33}\end{array}\right) \\ \left(\begin{array}{ccc}a_{11}&b_{1}&a_{13}\\a_{21}&b_{2}&a_{23}\\a_{31}&b_{3}&a_{33}\end{array}\right)\quad \xrightarrow{R_2=R_2-2R_3}\quad&\left(\begin{array}{ccc}a_{11}&b_{1}&a_{13} \\ a_{21}-2a_{31}&b_{2}-2b_{3}&a_{23}-2a_{33} \\ a_{31}&b_{3}&a_{33}\end{array}\right).\end{aligned}\]
   Зокрема,\(\det(A)\) і\(\det(A_i)\) є незмінними,\(\det(A)/\det(A_i)\) тому незмінні.
2. Масштабування рядка\((\,A\mid b\,)\) на коефіцієнт\(c\) масштабів одного і того ж рядка\(A\) і\(A_i\) на один і той же коефіцієнт:
   \[\begin{aligned}\left(\begin{array}{ccc|c}a_{11}&a_{12}&a_{13}&b_1 \\ a_{21}&a_{22}&a_{23}&b_2\\a_{31}&a_{32}&a_{33}&b_3\end{array}\right)\quad\xrightarrow{R_2=cR_2}\quad&\left(\begin{array}{ccc}a_{11}&a_{12}&a_{13}&b_1 \\ ca_{21}&ca_{22}&ca_{23}&cb_2\\a_{31}&a_{32}&a_{33}&b_3\end{array}\right) \\ \left(\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{array}\right)\quad\xrightarrow{R_2=cR_2}\quad&\left(\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\ca_{21}&ca_{22}&ca_{23} \\ a_{31}&a_{32}&a_{33}\end{array}\right) \\ \left(\begin{array}{ccc}a_{11}&b_{1}&a_{13}\\a_{21}&b_{2}&a_{23}\\a_{31}&b_{3}&a_{33}\end{array}\right)\quad\xrightarrow{R_2=cR_2}\quad&\left(\begin{array}{ccc}a_{11}&b_{1}&a_{13}\\ca_{21}&cb_{2}&ca_{23} \\ a_{31}&b_{3}&a_{33}\end{array}\right).\end{aligned}\]
   Зокрема,\(\det(A)\) і обидва\(\det(A_i)\) масштабуються на коефіцієнт\(c\text{,}\) так не\(\det(A_i)/\det(A)\) змінюється.
3. Поміняючи два ряди\((\,A\mid b\,)\) свопів однаковими рядками\(A\) і\(A_i\text{:}\)
   \[\begin{aligned}\left(\begin{array}{ccc|c}a_{11}&a_{12}&a_{13}&b_1 \\ a_{21}&a_{22}&a_{23}&b_2\\a_{31}&a_{32}&a_{33}&b_3\end{array}\right)\quad\xrightarrow{R_1\longleftrightarrow R_2}\quad&\left(\begin{array}{ccc|c}a_{21}&a_{22}&a_{23}&b_2\\a_{11}&a_{12}&a_{13}&b_1\\a_{31}&a_{32}&a_{33}&b_3\end{array}\right) \\ \left(\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{array}\right)\quad\xrightarrow{R_1\longleftrightarrow R_2}\quad&\left(\begin{array}{ccc}a_{21}&a_{22}&a_{23}\\a_{11}&a_{12}&a_{13}\\a_{31}&a_{32}&a_{33}\end{array}\right) \\  \left(\begin{array}{ccc}a_{11}&b_{1}&a_{13}\\a_{21}&b_{2}&a_{23}\\a_{31}&b_{3}&a_{33}\end{array}\right)\quad\xrightarrow{R_1\longleftrightarrow R_2}\quad&\left(\begin{array}{ccc}a_{21}&b_2&a_{23} \\ a_{11}&b_1&a_{13}\\a_{31}&b_3&a_{33}\end{array}\right).\end{aligned}\]
   зокрема,\(\det(A)\) і\(\det(A_i)\) обидва заперечуються,\(\det(A_i)/\det(A)\) тому не змінюється.

Приклад\(\PageIndex{9}\)

Обчислити рішення за\(Ax=b\) допомогою правила Крамера, де

\[ A = \left(\begin{array}{cc}a&b\\c&d\end{array}\right) \qquad b = \left(\begin{array}{c}1\\2\end{array}\right). \nonumber \]

Тут коефіцієнти\(A\) невідомі, але можна\(A\) вважати оборотними.

Рішення

Спочатку обчислюємо детермінанти матриць, одержуваних заміною стовпців\(A\) на на\(b\text{:}\)

\[\begin{array}{lll}A_1=\left(\begin{array}{cc}1&b\\2&d\end{array}\right)&\qquad&\det(A_1)=d-2b \\ A_2=\left(\begin{array}{cc}a&1\\c&2\end{array}\right)&\qquad&\det(A_2)=2a-c.\end{array}\nonumber\]

Тепер обчислюємо

\[ \frac{\det(A_1)}{\det(A)} = \frac{d-2b}{ad-bc} \qquad \frac{\det(A_2)}{\det(A)} = \frac{2a-c}{ad-bc}. \nonumber \]

Звідси випливає, що

\[ x = \frac 1{ad-bc}\left(\begin{array}{c}d-2b\\2a-c\end{array}\right). \nonumber \]

Тепер ми використовуємо правило Крамера, щоб довести першу\(\PageIndex{2}\) теорему цього підрозділу.

Доказ

Колонка\(A^{-1}\) - це\(x_j = A^{-1} e_j\).\(j\) Цей вектор є розв'язком матричного рівняння

\[ Ax = A\bigl(A^{-1} e_j\bigr) = I_ne_j = e_j. \nonumber \]

За правилом Крамера, запис\(x_j\) -\(A_i\) це\(\det(A_i)/\det(A)\text{,}\) де матриця, отримана з\(A\) заміною\(i\) го стовпця\(A\) на\(i\)\(e_j\text{:}\)

\[A_i=\left(\begin{array}{cccc}a_{11}&a_{12}&0&a_{14}\\a_{21}&a_{22}&1&a_{24}\\a_{31}&a_{32}&0&a_{34}\\a_{41}&a_{42}&0&a_{44}\end{array}\right)\quad (i=3,\:j=2).\nonumber\]

Розширюючи кофактори вздовж\(i\) го стовпця, ми бачимо детермінант\(A_i\) - це саме\((j,i)\)\(C_{ji}\) -кофактор\(A\). Тому\(j\) стовпець\(A^{-1}\) - це

\[ x_j = \frac 1{\det(A)}\left(\begin{array}{c}C_{ji}\\C_{j2}\\ \vdots \\ C_{jn}\end{array}\right), \nonumber \]

і таким чином

\[ A^{-1} = \left(\begin{array}{cccc}|&|&\quad&| \\ x_1&x_2&\cdots &x_n\\ |&|&\quad &|\end{array}\right) = \frac 1{\det(A)}\left(\begin{array}{ccccc}C_{11}&C_{21}&\cdots &C_{n-1,1}&C_{n1} \\ C_{12}&C_{22}&\cdots &C_{n-1,2}&C_{n2} \\ \vdots &\vdots &\ddots &\vdots &\vdots \\ C_{1,n-1}&C_{2,n-1}&\cdots &C_{n-1,n-1}&C{n,n-1} \\ C_{1n}&C_{2n}&\cdots &C_{n-1,n}&C_{nn}\end{array}\right). \nonumber \]