11.E: Графіки (вправи)

Last updated

Oct 27, 2022
Save as PDF
- 11.8: Зрозумійте нахил лінії (частина 2)
- 11.S: Графіки (резюме)

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

11.1 - Використання прямокутної системи координат

Графік точок у прямокутній системі координат

У наступних вправах розмістіть кожну точку в прямокутній системі координат.

(1, 3), (3, 1)
(2, 5), (5, 2)

У наступних вправах побудуйте кожну точку в прямокутній системі координат і визначте квадрант, в якому знаходиться точка.

(а) (−1, −5) (b) (−3, 4) (c) (2, −3) (d) $\left(1, \dfrac{5}{2}\right)$
(а) (3, −2) (b) (−4, −1) (c) (−5, 4) (d) $\left(2, \dfrac{10}{3}\right)$

Визначення точок на графіку

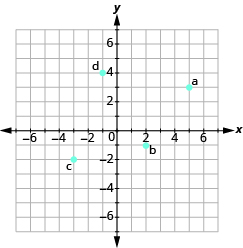
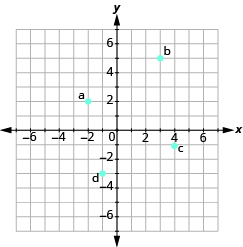
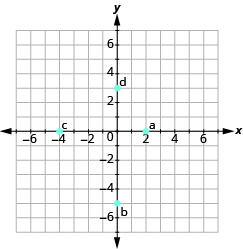
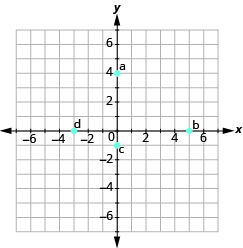
У наступних вправах назвіть впорядковану пару кожної точки, показаної в прямокутній системі координат.

$На графіку показана координатна площина x y. Осі йдуть від -7 до 7. «a» наноситься на 5, 3, «b» на 2, -1, «c» при -3, -2, а «d» при -1,4.$
$На графіку показана координатна площина x y. Осі йдуть від -7 до 7. «a» наноситься на -2, 2, «b» на 3, 5, «c» на 4, -1, а «d» при -1,3.$
$На графіку показана координатна площина x y. Осі йдуть від -7 до 7. «a» наноситься на 2, 0, «b» при 0, -5, «c» при -4,0, а «d» на 0,3.$
$На графіку показана координатна площина x y. Осі йдуть від -7 до 7. «a» позначається на 0, 4, «b» при 5, 0, «c» при 0, -1, а «d» при -3,0.$

Перевірка розв'язків рівняння у двох змінних

У наступних вправах знайдіть впорядковані пари, які є розв'язками даного рівняння.

5х+ у = 10
1. (5, 1)
2. (2, 0)
3. (4, −10)
y = 6х − 2
1. (1, 4)
2. $\left(\dfrac{1}{3} , 0\right)$
3. (6, −2)

Заповніть таблицю розв'язків лінійного рівняння у двох змінних

У наступних вправах заповніть таблицю, щоб знайти рішення кожного лінійного рівняння.

y = 4х − 1

х	у	(х, у)
0
1
-2

у = $− \dfrac{1}{2}$ х + 3

х	у	(х, у)
0
1
-2

х + 2г = 5

х	у	(х, у)
	0
1
-1

3x − 2г = 6

х	у	(х, у)
0
	0
-2

Пошук розв'язків лінійного рівняння у двох змінних

У наступних вправах знайдіть три рішення кожного лінійного рівняння.

х + у = 3
х + у = −4
у = 3х+ 1
y = − x − 1

11.2 - Графічні лінійні рівняння

Визнати зв'язок між розв'язками рівняння та його графіком

У наступних вправах для кожної впорядкованої пари вирішіть (а), чи є впорядкована пара рішенням рівняння. (б) якщо точка знаходиться на лінії.

y = − х + 4
1. (0, 4)
2. (−1, 3)
3. (2, 2)
4. (−2, 6)

$На графіку показана координатна площина x y. Осі йдуть від -7 до 7. Через точки «впорядкована пара 0, 4» і «впорядкована пара 4, 0» проходить лінія.$

y = $\dfrac{2}{3}$ х − 1
1. (0, −1)
2. (3, 1)
3. (−3, −3)
4. (6, 4)

$На графіку показана координатна площина x y. Осі йдуть від -7 до 7. Через точки «впорядкована пара 0, -1» і «впорядкована пара 3, 1» проходить лінія.$

Графік лінійного рівняння шляхом побудови точок

У наступних вправах граф за допомогою побудови точок.

y = 4х − 3
y = −3х
2х+ у = 7

Графік Вертикальні та Горизонтальні лінії

У наступних вправах проведіть графік вертикальних або горизонтальних ліній.

y = −2
х = 3

11.3 - Графік з перехопленнями

Визначте перехоплення на графіку

У наступних вправах знайдіть x- і y-перехоплення.

$На графіку показана координатна площина x y. Осі йдуть від -7 до 7. Через точки «впорядкована пара 0, 4» і «впорядкована пара -4, 0» проходить лінія.$
$На графіку показана координатна площина x y. Вісь x проходить від -1 до 6. Вісь Y проходить від -4 до 2. Через точки «впорядкована пара 5, 1» і «впорядкована пара 0, -3» проходить лінія.$

Знайти перехоплення з рівняння прямої

У наступних вправах знайдіть перехоплення.

х + у = 5
x − y = −1
y = $\dfrac{3}{4}$ х − 12
у = 3х

Графік лінії за допомогою перехоплення

У наступних вправах граф з використанням перехоплень.

−х + 3й = 3
х + у = −2

Виберіть найбільш зручний метод для побудови графіка лінії

У наступних вправах визначте найбільш зручний метод для графіка кожного рядка.

х = 5
y = −3
2х+ у = 5
x × y = 2
у = $\dfrac{1}{2}$ х + 2
y = $\dfrac{3}{4}$ х − 1

11.4 - Розуміння нахилу лінії

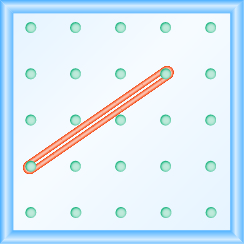
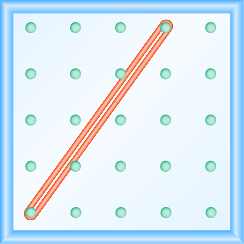
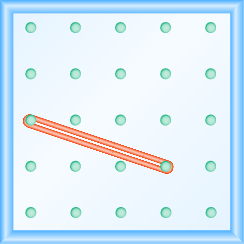
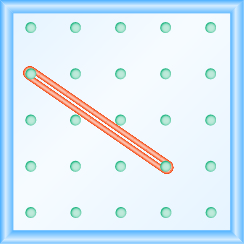
Використання геобалок для моделювання схилу

У наступних вправах знайдіть нахил, змодельований на кожній геоборді.

$На малюнку зображена сітка з рівномірно розташованих точок. Є 5 рядків і 5 стовпців. Існує петля стилю гумки, що з'єднує точку в стовпці 1 ряд 4 і точку в стовпці 4 ряд 2.$
$На малюнку зображена сітка з рівномірно розташованих точок. Є 5 рядків і 5 стовпців. Існує петля стилю гумки, що з'єднує точку в стовпці 1 ряд 5 і точку в стовпці 4 ряд 1.$
$На малюнку зображена сітка з рівномірно розташованих точок. Є 5 рядків і 5 стовпців. Існує петля стилю гумки, що з'єднує точку в стовпці 1 ряд 3 і точку в стовпці 4 ряд 4.$
$На малюнку зображена сітка з рівномірно розташованих точок. Є 5 рядків і 5 стовпців. Існує петля стилю гумки, що з'єднує точку в стовпці 1 ряд 2 і точку в стовпці 4 ряд 4.$

У наступних вправах змоделюйте кожен нахил. Намалюйте картинку, щоб показати свої результати.

$\dfrac{1}{3}$
$\dfrac{3}{2}$
$− \dfrac{2}{3}$
$− \dfrac{1}{2}$

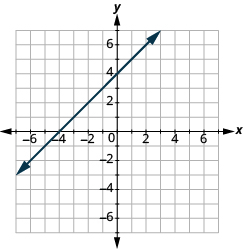
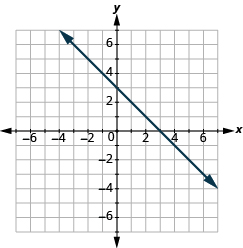
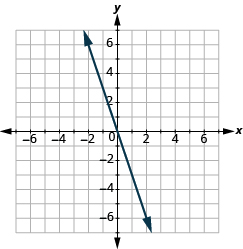
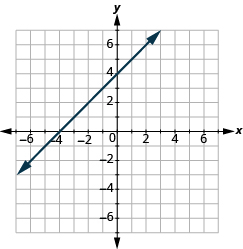
Знайти нахил прямої з її графіка

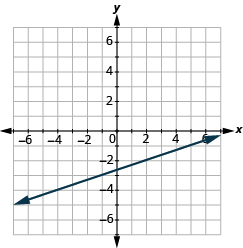
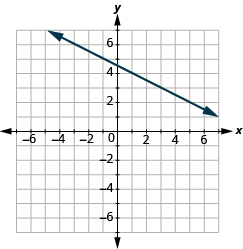
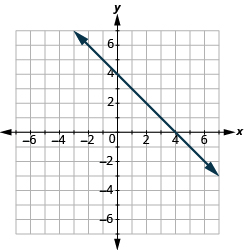
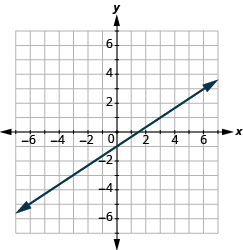
У наступних вправах знайдіть нахил кожної показаної лінії.

$На графіку показана координатна площина x y. Осі йдуть від -7 до 7. Через точки «впорядкована пара 0, 0» і «впорядкована пара 2, -6» проходить лінія.$
$На графіку показана координатна площина x y. Осі йдуть від -7 до 7. Через точки «впорядкована пара 0, 4» і «впорядкована пара -4, 0» проходить лінія.$
$На графіку показана координатна площина x y. Осі йдуть від -7 до 7. Лінія проходить через точки «впорядкована пара -4, -4» і «впорядкована пара 5, -1».$
$На графіку показана координатна площина x y. Осі йдуть від -7 до 7. Через точки «впорядкована пара -3, 6» і «впорядкована пара 5, 2» проходить лінія.$

Знайти нахил горизонтальних і вертикальних ліній

У наступних вправах знайдіть нахил кожної лінії.

у = 2
х = 5
x = −3
y = −1

Використовуйте формулу нахилу, щоб знайти нахил лінії між двома точками

У наступних вправах використовуйте формулу нахилу, щоб знайти нахил лінії між кожною парою точок.

(2, 1), (4, 5)
(−1, −1), (0, −5)
(3, 5), (4, −1)
(−5, −2), (3, 2)

Графік лінії з заданою точкою та нахилом

У наступних вправах графуйте лінію, задану точку та нахил.

(2, −2); м = $\dfrac{5}{2}$
(−3, 4); м = $− \dfrac{1}{3}$

Вирішіть програми нахилу

У наступній вправі вирішите застосування нахилу.

Дах має підйом 10 футів і запустити 15 футів. Який її нахил?

ПРАКТИКА ТЕСТ

Побудуйте і позначте ці пункти:
1. (2, 5)
2. (−1, −3)
3. (−4, 0)
4. (3, −5)
5. (−2, 1)
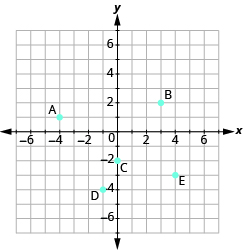
Назвіть впорядковану пару для кожної показаної точки.

$На графіку показана координатна площина x y. Осі простягаються від -7 до 7. А наноситься на рівні -4, 1, В при 3, 2, С при 0, -2, D при -1, -4, і Е при 4, -3.$

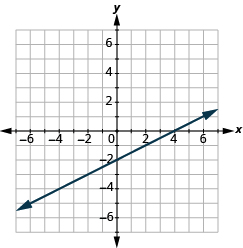
Знайдіть перехоплення x та y-перехоплення на показаній лінії.

$На графіку показана координатна площина x y. Вісь х проходить від -7 до 7. Вісь Y проходить від -7 до 7. Через точки «впорядкована пара 4, 0» і «впорядкована пара 0, -2» проходить лінія.$

Знайти x-перехоплення та y-перехоплення рівняння 3x − y = 6.
Чи є (1, 3) розв'язком рівняння x + 4y = 12? Звідки ти знаєш?
Заповніть таблицю, щоб знайти чотири розв'язки рівняння y = − x + 1.

х	у	(х, у)
0
1
3
-2

Заповніть таблицю, щоб знайти три рішення рівняння 4x + y = 8.

х	у	(х, у)
0
	0
3

У наступних вправах знайдіть три рішення кожного рівняння, а потім графік кожного рядка.

y = −3х
2х+ 3й = −6

У наступних вправах знайдіть нахил кожної лінії.

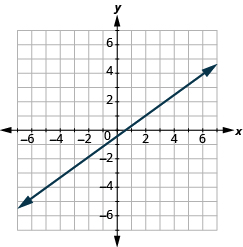
$На графіку показана координатна площина x y. Осі йдуть від -7 до 7. Вісь Y проходить від -5 до -4. Через точки «впорядкована пара 6, 4» і «впорядкована пара 0, -3» проходить лінія.$
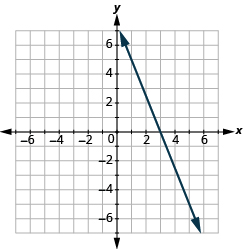
$На графіку показана координатна площина x y. Осі йдуть від -7 до 7. Через точки «впорядкована пара 3, 0» і «впорядкована пара 1, 5» проходить лінія.$
Використовуйте формулу нахилу, щоб знайти нахил прямої між (0, −4) та (5, 2).
Знайти нахил лінії y = 2.
Графік лінії, що проходить через (1, 1) з ухилом m = $\dfrac{3}{2}$ .
Велосипедний маршрут піднімається на 20 футів для 1000 футів горизонтальної відстані. Що таке ухил траси?

Автори та атрибуція

Template:ContribOpenStaxPreAlgebra