Skip to main content
LibreTexts - Ukrayinska

11.8: Зрозумійте нахил лінії (частина 2)

  1. Last updated
  2. Save as PDF
  • Page ID
    57801

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Графік лінії з заданою точкою та нахилом

    У цьому розділі ми графували лінії шляхом побудови точок, використовуючи перехоплення та розпізнаючи горизонтальні та вертикальні лінії.

    Іншим методом, який ми можемо використовувати для графіків ліній, є метод точкового нахилу. Іноді нам буде дана одна точка і нахил прямої, замість її рівняння. Коли це відбувається, ми використовуємо визначення нахилу, щоб намалювати графік лінії.

    Приклад\(\PageIndex{11}\):

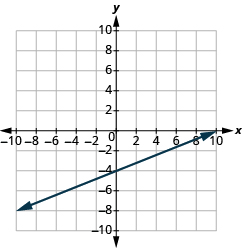
    Графік лінії, що проходить через точку (1, −1), нахил якої дорівнює m =\(\dfrac{3}{4}\).

    Рішення

    Побудуйте задану точку, (1, −1).

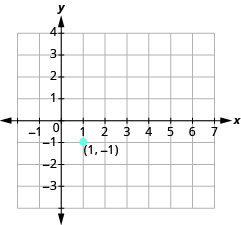
    На графіку показана координатна площина x y. Вісь x проходить від -1 до 7. Вісь Y проходить від -3 до 4. Позначена точка малюється на «впорядкованій парі 1, -1».

    Використовуйте формулу нахилу m =\(\dfrac{rise}{run}\), щоб визначити підйом і пробіг.

    \[\begin{split} m &= \dfrac{3}{4} \\ \dfrac{rise}{run} &= \dfrac{3}{4} \\ rise &= 3 \\ run &= 4 \end{split}\]

    Починаючи з наміченої нами точки, відраховуємо підйом і біжимо, щоб відзначити другу точку. Ми вважаємо 3 одиниці вгору і 4 одиниці вправо.

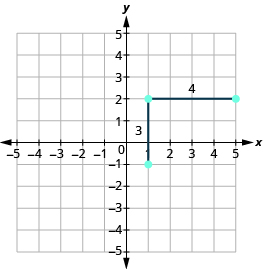
    На графіку показана координатна площина x y. Обидві осі проходять від -5 до 5. Промальовуються два відрізка лінії. Вертикальний відрізок лінії з'єднує точки «впорядкована пара 1, -1» і «пара порядку «1, 2». Він має маркування «3». Відрізок горизонтальної лінії починається у верхній частині відрізка вертикальної лінії і йде вправо, з'єднуючи точки «впорядкована пара 1, 2» і «впорядкована пара 5, 2». Він має маркування «4».

    Потім з'єднуємо точки лінією і малюємо стрілки на кінцях, щоб показати, що триває.

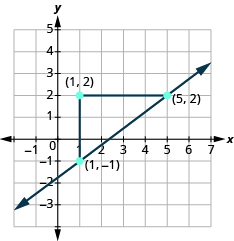
    На графіку показана координатна площина x y. Вісь X проходить від -3 до 5. Вісь Y проходить від -1 до 7. Дві немічені точки намальовані на «впорядкована пара 1, -1» та «впорядкована пара 5, 2». Через точки проходить лінія. Два відрізка лінії утворюють трикутник з лінією. Вертикальна лінія з'єднує «впорядковану пару 1, -1» і «впорядковану пару 1, 2». Горизонтальний відрізок лінії з'єднує «впорядковану пару 1, 2» і «впорядковану пару 5, 2».

    Ми можемо перевірити нашу лінію, починаючи з будь-якої точки і підрахувавши 3 і вправо 4. Ми повинні дістатися до іншої точки на лінії.

    Вправа\(\PageIndex{21}\):

    Графік лінії, що проходить через точку з заданим нахилом:

    (2, −2), м =\(\dfrac{4}{3}\)

    Відповідь

    На графіку показана координатна площина x y. Вісь х проходить від -12 до 12. Вісь Y проходить від -12 до 12. Через точки «впорядкована пара -2, 3» і «впорядкована пара 8, 6» проходить лінія.

    Вправа\(\PageIndex{22}\):

    Графік лінії, що проходить через точку з заданим нахилом:

    (−2, 3), м =\(\dfrac{1}{4}\)

    Відповідь

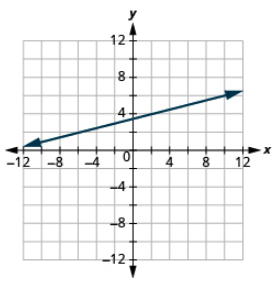
    На графіку показана координатна площина x y. Вісь х проходить від -12 до 12. Вісь Y проходить від -12 до 12. Через точки «впорядкована пара -2, 3» і «впорядкована пара 2, 4» проходить лінія.

    ЯК: ГРАФІК ЛІНІЇ З ЗАДАННЯМ ТОЧКИ ТА НАХИЛУ

    Крок 1. Ділянка заданої точки.

    Крок 2. Використовуйте формулу нахилу, щоб визначити підйом і пробіг.

    Крок 3. Починаючи з заданої точки, відраховуйте підйом і біжіть, щоб відзначити другу точку.

    Крок 4. З'єднайте точки лінією.

    Приклад\(\PageIndex{12}\):

    Графік лінії з y -перехопленням (0, 2) і нахилом m =\(− \dfrac{2}{3}\).

    Рішення

    Побудуйте задану точку, y -перехоплення (0, 2).

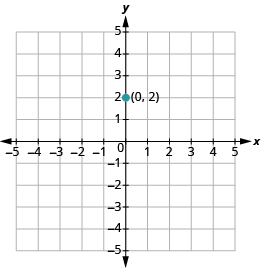
    На графіку показана координатна площина x y. Вісь x проходить від -1 до 4. Вісь Y проходить від -1 до 3. Позначено пункт «впорядкована пара 0, 2».

    Використовуйте формулу нахилу m = підйом пробігу, щоб визначити підйом і пробіг.

    \[\begin{split} m &= − \dfrac{2}{3} \\ \dfrac{rise}{run} &= \dfrac{−2}{3} \\ rise &= –2 \\ run &= 3 \end{split}\]

    Починаючи з (0, 2), порахуйте підйом і біг і відзначте другу точку.

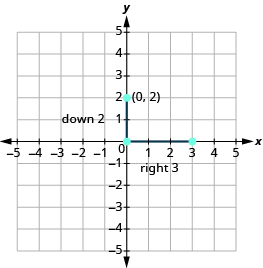
    На графіку показана координатна площина x y. Обидві осі проходять від -5 до 5. Вертикальний відрізок лінії з'єднує точки на «впорядкованій парі 0, 2» і «впорядкована пара 0, 0» і має позначення «вниз 2». Горизонтальний відрізок лінії з'єднує «впорядковану пару 0, 0» і «впорядковану пару 0, 3» і має позначення «права 3».

    З'єднайте точки лінією.

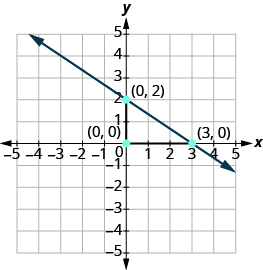
    На графіку показана координатна площина x y. Обидві осі проходять від -5 до 5. Дві мічені точки намальовані на «впорядкована пара 0, 2» та «впорядкована пара 3, 0». Через точки проходить лінія. Два відрізка лінії утворюють трикутник з лінією. Вертикальна лінія з'єднує «впорядковану пару 0, 2» і «впорядковану пару 0, 0». Горизонтальний відрізок лінії з'єднує «впорядковану пару 0, 0» і «впорядковану пару 3, 0».

    Вправа\(\PageIndex{23}\):

    Графік лінії з заданим перехопленням і нахилом:

    y-перехоплення 4, м =\(− \dfrac{5}{2}\)

    Відповідь

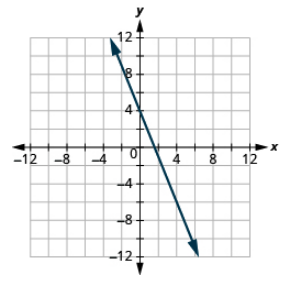
    На графіку показана координатна площина x y. Вісь х проходить від -12 до 12. Вісь Y проходить від -12 до 12. Через точки «впорядкована пара 0, 4» і «впорядкована пара 4, -6» проходить лінія.

    Вправа\(\PageIndex{24}\):

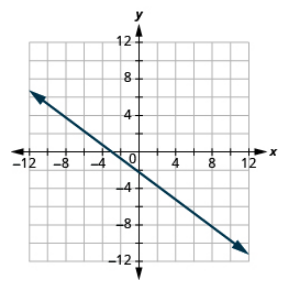
    Графік лінії з заданим перехопленням і нахилом:

    x-перехоплення −3, m =\(− \dfrac{3}{4}\)

    Відповідь

    На графіку показана координатна площина x y. Вісь х проходить від -12 до 12. Вісь Y проходить від -12 до 12. Через точки «впорядкована пара -3, 0» і «впорядкована пара 8, -8» проходить лінія.

    Приклад\(\PageIndex{13}\):

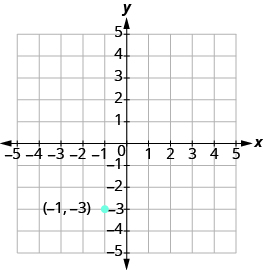
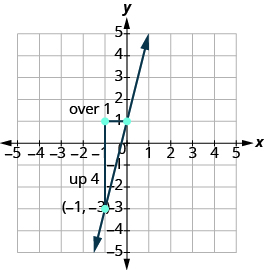
    Графік лінії, що проходить через точку (−1, −3), нахил якої дорівнює m = 4.

    Рішення

    Ділянка заданої точки.

    На графіку показана координатна площина x y. Обидві осі проходять від -5 до 5. Маркується точка «впорядкована пара -1, -3».

    Визначте підйом і біг. $m = 4\ тег {11.4.44} $$
    Запишіть 4 як дріб. $\ dfrac {підйом} {прогін} =\ dfrac {4} {1}\ тег {11.4.45} $$
      підйом = 4, пробіг = 1

    Підрахуйте підйом і біжіть.

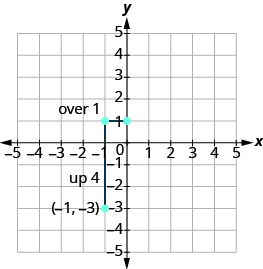
    На графіку показана координатна площина x y. Обидві осі проходять від -5 до 5. Вісь Y проходить від -4 до 2. Відрізок вертикальної лінії з'єднує точки «впорядкована пара -1, -3» і «впорядкована пара -1, 1» і позначається «вгору 4». Горизонтальний відрізок лінії з'єднує «впорядковану пару -1, 1» і «впорядковану пару 0, 1» і має маркування «більше 1».

    Відзначте другий пункт. З'єднайте дві точки лінією.

    На графіку показана координатна площина x y. Обидві осі проходять від -5 до 5. Дві мічені точки намальовані на «впорядкована пара -1, -3» та «впорядкована пара -1, 1». Через точки проходить лінія. Два відрізка лінії утворюють трикутник з лінією. Вертикальна лінія з'єднує «впорядковану пару -1, -3» і «впорядковану пару -1, 1». Він позначений «вгору 4». Горизонтальний відрізок лінії з'єднує «впорядковану пару -1, 1» і «впорядковану пару 0, 1». Він позначений «більше 1»

    Вправа\(\PageIndex{25}\):

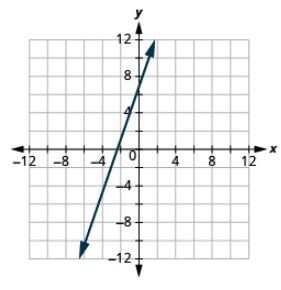
    Графік лінії з заданим перехопленням і нахилом: (−2, 1), m = 3.

    Відповідь

    На графіку показана координатна площина x y. Вісь х проходить від -7 до 7. Вісь Y проходить від -7 до 7. Через точки «впорядкована пара -2, 1» і «впорядкована пара 0, 7» проходить лінія.

    Вправа\(\PageIndex{26}\):

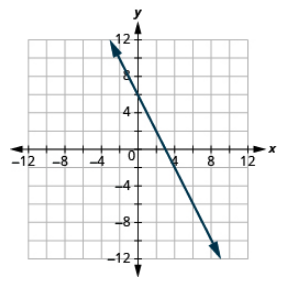
    Графік лінії з заданим перехопленням і нахилом: (4, −2), m = −2.

    Відповідь

    На графіку показана координатна площина x y. Вісь х проходить від -7 до 7. Вісь Y проходить від -7 до 7. Через точки «впорядкована пара 0, 6» і «впорядкована пара 0, 3» проходить лінія.

    Вирішіть програми нахилу

    На початку цього розділу ми сказали, що існує багато застосувань нахилу в реальному світі. Давайте розглянемо декілька зараз.

    Приклад\(\PageIndex{14}\):

    Крок даху будівлі - це нахил покрівлі. Знання поля важливо в кліматі, де є сильний снігопад. Якщо дах занадто рівна, то вага снігу може стати причиною її обвалення. Який ухил покрівлі показаний?

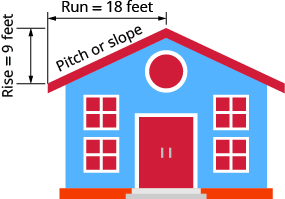
    На цьому малюнку зображений будинок з похилим дахом. Дах на одній половині будівлі маркується «ухил покрівлі». Існує відрізок лінії зі стрілками на кожному кінці, що вимірює вертикальну довжину даху і позначений «підйом = 9 футів». Існує відрізок лінії зі стрілками на кожному кінці, що вимірює горизонтальну довжину кореня і позначений «пробіг = 18 футів».

    Рішення

    Скористайтеся формулою нахилу. $$m =\ dfrac {підйом} {запустити}\ тег {11.4.46} $$
    Підставте значення на підйом і біг. $ $ м =\ дфрак {9\; фут} {18\; фут}\ тег {11.4.47} $$
    Спростити. $$m =\ дфрак {1} {2}\ тег {11.4.48} $$
      Ухил покрівлі є\(\dfrac{1}{2}\).
    Вправа\(\PageIndex{27}\):

    Знайдіть ухил, що дають підйом і виконайте: Дах з підйомом = 14 і пробігом = 24.

    Відповідь

    \(\frac{7}{12}\)

    Вправа\(\PageIndex{28}\):

    Знайдіть ухил, що дають підйом і виконайте: Дах з підйомом = 15 і пробігом = 36.

    Відповідь

    \(\frac{5}{12}\)

    Ви коли-небудь замислювалися над каналізаційними трубами, що йдуть з вашого будинку на вулицю? Їх нахил є важливим фактором того, як вони забирають відходи з вашого будинку.

    Приклад\(\PageIndex{15}\):

    Каналізаційні труби повинні\(\dfrac{1}{4}\) нахилятися вниз дюйм на фут, щоб правильно стікати. Який необхідний ухил?

    На цьому малюнку зображений прямокутний трикутник. Коротка ніжка вертикальна і має маркування «1 більше 4 дюймів». Довга нога з написом «1 фут».

    Рішення

    Скористайтеся формулою нахилу. $ $ м =\ dfrac {підйом} {прогін} =\ dfrac {-\ dfrac {1} {4}\; в.} {1\; ft}\ тег {11.4.49} $$
    Перетворіть 1 фут на 12 дюймів. $ $ м =\ dfrac {-\ dfrac {1} {4}\; в.} {12\; в}\ тег {11.4.50} $$
    Спростити. $$m = -\ dfrac {1} {48}\ тег {11.4.51} $$
      Ухил труби є\(− \dfrac{1}{48}\).
    Вправа\(\PageIndex{29}\):

    Знайдіть нахил труби: Труба нахиляється вниз\(\dfrac{1}{3}\) дюйм на фут.

    Відповідь

    \(-\frac{1}{36}\)

    Вправа\(\PageIndex{30}\):

    Знайдіть нахил труби: Труба нахиляється вниз\(\dfrac{3}{4}\) дюйм на ярд.

    Відповідь

    \(-\frac{1}{48}\)

    ДОСТУП ДО ДОДАТКОВИХ ОНЛАЙН-РЕСУРСІВ

    Визначення позитивного нахилу з графіка

    Визначити негативний нахил з графіка

    Визначте нахил від двох точок

    Практика робить досконалим

    Використання геобалок для моделювання схилу

    У наступних вправах знайдіть нахил, змодельований на кожній геоборді.

    1. На малюнку зображена сітка з рівномірно розташованих точок. Є 5 рядків і 5 стовпців. Існує петля стилю гумки, що з'єднує точку в стовпці 1 ряд 3 і точку в стовпці 5 ряд 2.
    2. На малюнку зображена сітка з рівномірно розташованих точок. Є 5 рядків і 5 стовпців. Існує петля стилю гумки, що з'єднує точку в стовпці 2 ряд 4 і точку в стовпці 5 ряд 2.
    3. На малюнку зображена сітка з рівномірно розташованих точок. Є 5 рядків і 5 стовпців. Існує петля стилю гумки, що з'єднує точку в стовпці 2 ряд 1 і точку в стовпці 4 ряд 4.
    4. На малюнку зображена сітка з рівномірно розташованих точок. Є 5 рядків і 5 стовпців. Існує петля стилю гумки, що з'єднує точку в стовпці 2 ряд 1 і точку в стовпці 4 ряд 4.

    У наступних вправах моделюйте кожен нахил. Намалюйте картинку, щоб показати свої результати.

    1. \(\dfrac{2}{3}\)
    2. \(\dfrac{3}{4}\)
    3. \(\dfrac{1}{4}\)
    4. \(\dfrac{4}{3}\)
    5. \(- \dfrac{1}{2}\)
    6. \(- \dfrac{3}{4}\)
    7. \(- \dfrac{2}{3}\)
    8. \(- \dfrac{3}{2}\)

    Знайти нахил прямої з її графіка

    У наступних вправах знайдіть нахил кожної показаної лінії.

    1. На графіку показана координатна площина x y. Вісь х проходить від -10 до 10. Вісь Y проходить від -10 до 10. Лінія проходить через точки «впорядкована пара 0, -4» і «впорядкована пара 10, 0».
    2. На графіку показана координатна площина x y. Вісь х проходить від -10 до 10. Вісь Y проходить від -10 до 10. Лінія проходить через точки «впорядкована пара 0, -5» і «впорядкована пара 3, 0».
    3. На графіку показана координатна площина x y. Вісь х проходить від -12 до 12. Вісь Y проходить від -12 до 12. Через точки «впорядкована пара 0, -1» і «впорядкована пара 1, 0» проходить лінія.
    4. На графіку показана координатна площина x y. Вісь х проходить від -10 до 10. Вісь Y проходить від -10 до 10. Через точки «впорядкована пара 0, 3» і «впорядкована пара 6, 0» проходить лінія.
    5. На графіку показана координатна площина x y. Вісь х проходить від -10 до 10. Вісь Y проходить від -10 до 10. Через точки «впорядкована пара 0, 2» і «впорядкована пара 6, 0» проходить лінія.
    6. На графіку показана координатна площина x y. Вісь х проходить від -10 до 10. Вісь Y проходить від -10 до 10. Через точки «впорядкована пара 0, 2» і «впорядкована пара 6, 0» проходить лінія.
    7. На графіку показана координатна площина x y. Вісь х проходить від -10 до 10. Вісь Y проходить від -10 до 10. Через точки «впорядкована пара 0, 6» і «впорядкована пара 8, 0» проходить лінія.
    8. На графіку показана координатна площина x y. Вісь х проходить від -10 до 10. Вісь Y проходить від -10 до 10. Через точки «впорядкована пара -1, 0» і «впорядкована пара 0, -1» проходить лінія.
    9. На графіку показана координатна площина x y. Вісь х проходить від -10 до 10. Вісь Y проходить від -10 до 10. Лінія проходить через точки «впорядкована пара -4, 0» і «впорядкована пара -4, 6».
    10. На графіку показана координатна площина x y. Вісь х проходить від -10 до 10. Вісь Y проходить від -10 до 10. Через точки «впорядкована пара -2, 0» і «впорядкована пара 4, 4» проходить лінія.
    11. На графіку показана координатна площина x y. Вісь х проходить від -10 до 10. Через точки «впорядкована пара 0, 4» і «впорядкована пара 4, -6» проходить лінія.
    12. На графіку показана координатна площина x y. Вісь х проходить від -10 до 10. Через точки «впорядкована пара 0, 4» і «впорядкована пара 4, -6» проходить лінія.
    13. На графіку показана координатна площина x y. Вісь х проходить від -10 до 10. Через точки «впорядкована пара 1, 4» і «впорядкована пара 7, 0» проходить лінія.
    14. На графіку показана координатна площина x y. Вісь х проходить від -10 до 10. Через точки «впорядкована пара 0, 3» і «впорядкована пара 7, 0» проходить лінія.
    15. На графіку показана координатна площина x y. Вісь х проходить від -10 до 10. Через точки «впорядкована пара 2, 0» і «впорядкована пара 10, 4» проходить лінія.
    16. На графіку показана координатна площина x y. Вісь х проходить від -10 до 10. Через точки «впорядкована пара 6, 2» і «впорядкована пара 0, -3» проходить лінія.

    Знайти нахил горизонтальних і вертикальних ліній

    У наступних вправах знайдіть нахил кожної лінії.

    1. у = 3
    2. у = 1
    3. х = 4
    4. х = 2
    5. y = −2
    6. y = −3
    7. х = −5
    8. х = −4

    Використовуйте формулу нахилу, щоб знайти нахил лінії між двома точками

    У наступних вправах використовуйте формулу нахилу, щоб знайти нахил лінії між кожною парою точок.

    1. (1, 4), (3, 9)
    2. (2, 3), (5, 7)
    3. (0, 3), (4, 6)
    4. (0, 1), (5, 4)
    5. (2, 5), (4, 0)
    6. (3, 6), (8, 0)
    7. (−3, 3), (2, −5)
    8. (−2, 4), (3, −1)
    9. (−1, −2), (2, 5)
    10. (−2, −1), (6, 5)
    11. (4, −5), (1, −2)
    12. (3, −6), (2, −2)

    Графік лінії з заданою точкою та нахилом

    У наступних вправах наведіть графік лінії з заданою точкою і нахилом.

    1. (1, −2); м =\(\dfrac{3}{4}\)
    2. (1, −1); м =\(\dfrac{1}{2}\)
    3. (2, 5); м =\(− \dfrac{1}{3}\)
    4. (1, 4); м =\(− \dfrac{1}{2}\)
    5. (−3, 4); м =\(− \dfrac{3}{2}\)
    6. (−2, 5); м =\(− \dfrac{5}{4}\)
    7. . (−1, −4); м =\(\dfrac{4}{3}\)
    8. (−3, −5); м =\(\dfrac{3}{2}\)
    9. (0, 3); м =\(− \dfrac{2}{5}\)
    10. (0, 5); м =\(− \dfrac{4}{3}\)
    11. (−2, 0); м =\(−\dfrac{3}{4}\)
    12. (−1, 0); м =\(\dfrac{1}{5}\)
    13. (−3, 3); м = 2
    14. (−4, 2); м = 4
    15. (1, 5); м = −3
    16. (2, 3); м = −1

    Вирішіть програми нахилу

    У наступних вправах вирішуйте ці програми нахилу.

    1. Ухил покрівлі Досить простий спосіб визначити ухил - взяти 12-дюймовий рівень і встановити його одним кінцем на поверхні даху. Потім візьміть рулетку або лінійку, і відміряйте від іншого кінця рівня вниз до поверхні даху. Ви можете скористатися цими вимірами для розрахунку ухилу покрівлі. Який ухил даху на цій картині?

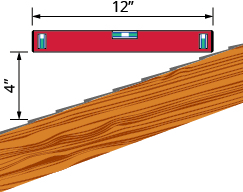
    На малюнку зображена дерев'яна дошка по діагоналі, що представляє збоку зріз скатного даху. Відрізок вертикальної лінії зі стрілками на обох кінцях вимірює вертикальну зміну висоти даху і має маркування «4 дюйми». Інструмент рівня знаходиться в горизонтальному положенні над дошкою і над ним - відрізок лінії зі стрілками на обох кінцях з позначкою «12 дюймів».

    1. Який ухил покрівлі показаний?

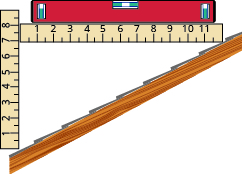
    На малюнку зображений діагональний зріз похилого даху. Лінійка у вертикальному положенні знаходиться внизу сегмента покрівлі і показує одиниці міток з 1 по 8 і продовжує ще одну одиницю. Друга лінійка починається від мітки «7» вертикальної лінійки і простягається горизонтально, поки вона не потрапить на піднімається дах. Горизонтальна лінійка має мітки одиниць з 1 по 11 і подовжує ще одну одиницю.

    1. Дорога класу А місцева дорога має клас 6%. Клас дороги - це її ухил, виражений у відсотках.
      1. Знайдіть ухил дороги у вигляді дробу, а потім спростіть дріб.
      2. Який підйом і біг відображали б цей схил або ухил?
    2. Шосе класу А місцева дорога піднімається на 2 фути на кожні 50 футів шосе.
      1. Що таке ухил магістралі?
      2. Клас магістралі - це його ухил, виражений у відсотках. Який сорт цієї магістралі?

    Щоденна математика

    1. Пандус для інвалідних колясок Правила для пандусів для інвалідних колясок вимагають максимального підйому на 1 дюйм для пробігу 12 дюймів.
      1. Скільки повинен бути пандус, щоб вмістити 24-дюймовий підйом до дверей?
      2. Намалюйте модель цього пандуса.
    2. Пандус для інвалідного візка Підйом на 1 дюйм для 16-дюймового пробігу полегшує для інвалідного візка піднятися на рампу.
      1. Скільки повинен бути пандус, щоб легко вмістити 24-дюймовий підйом до дверей?
      2. Намалюйте модель цього пандуса.

    Письмові вправи

    1. Що говорить про лінію знак схилу?
    2. Чим графік прямої з ухилом m =\(\dfrac{1}{2}\) відрізняється від графа прямої з ухилом m = 2?
    3. Чому нахил вертикальної лінії невизначений?
    4. Поясніть, як можна навести графік лінії з заданою точкою та її нахилом.

    Самостійна перевірка

    (а) Після виконання вправ використовуйте цей контрольний список, щоб оцінити своє володіння цілями цього розділу.

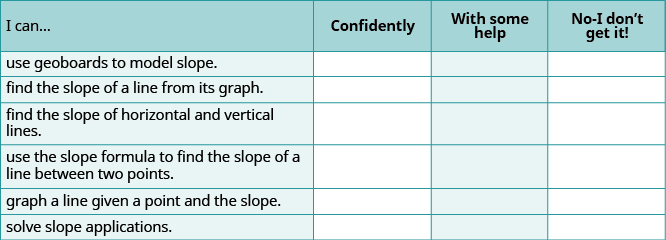
    CNX_BMath_Figure_AppB_069.jpg

    (b) За шкалою 1—10, як би ви оцінили своє володіння цим розділом у світлі ваших відповідей на контрольний список? Як ви можете це покращити?

    Автори та атрибуція