Skip to main content
LibreTexts - Ukrayinska

11.3: Графічні лінійні рівняння (частина 1)

  1. Last updated
  2. Save as PDF
  • Page ID
    57768

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання
    • Розпізнати зв'язок між розв'язками рівняння та його графіком
    • Графік лінійного рівняння шляхом побудови точок
    • Графік вертикальних і горизонтальних ліній
    будьте готові!

    Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

    1. Оцінити: 3x + 2, коли x = −1. Якщо ви пропустили цю проблему, перегляньте приклад 3.8.10.
    2. Вирішіть формулу: 5x + 2y = 20 для y. якщо ви пропустили цю проблему, перегляньте приклад 9.11.6.
    3. Спростити:\(\dfrac{3}{8}\) (−24). Якщо ви пропустили цю проблему, перегляньте приклад 4.3.10.

    Визнати зв'язок між розв'язками рівняння та його графіком

    У розділі Використання прямокутної системи координат ми знайшли кілька рішень рівняння 3x+ 2y = 6. Вони перераховані в таблиці нижче. Отже, впорядковані пари (0, 3), (2, 0),\(\left(1, \dfrac{3}{2}\right)\), (4, − 3) є деякими розв'язками рівняння 3x + 2y = 6. Ми можемо побудувати ці розв'язки в прямокутній системі координат, як показано на графіку праворуч.

    ...

    Зверніть увагу, як точки ідеально вирівняються? Точки з'єднуємо прямою лінією, щоб отримати графік рівняння 3х + 2y = 6. Зверніть увагу на стрілки на кінцях кожної сторони лінії. Ці стрілки вказують на продовження лінії.

    ...

    Кожна точка на прямій є розв'язком рівняння. Крім того, кожне рішення цього рівняння є точкою на цій лінії. Окуляри не на лінії - це не рішення!

    Зверніть увагу, що точка, координати якої (− 2, 6) знаходиться на лінії, показаної на малюнку\(\PageIndex{1}\). Якщо ви підставите x = − 2 та y = 6 у рівняння, ви виявите, що це рішення рівняння.

    ...

    Малюнок\(\PageIndex{1}\)

    Отже (4, 1) не є розв'язком рівняння 3х+ 2y = 6. Тому точка (4, 1) знаходиться не на лінії. Це приклад приказки: «Картина варта тисячі слів». Лінія показує всі розв'язки рівняння. Кожна точка на прямій є розв'язком рівняння. І кожне рішення цього рівняння знаходиться на цій лінії. Цей рядок називається графом рівняння 3x + 2y = 6.

    Означення: Графік лінійного рівняння

    Графік лінійного рівняння Ax+ By = C є прямою лінією.

    • Кожна точка на прямій є розв'язком рівняння.
    • Кожен розв'язок цього рівняння є точкою на цій лінії.
    Приклад\(\PageIndex{1}\):

    Графік y = 2x − 3 наведено нижче.

    ...

    Для кожної впорядкованої пари вирішите (а) Чи є впорядкована пара розв'язком рівняння? (б) Чи є точка на лінії?

    (а) (0, 3) (b) (3, − 3) (c) (2, − 3) (d) (− 1, − 5)

    Рішення

    Підставте x - і y -значення в рівняння, щоб перевірити, чи є впорядкована пара рішенням рівняння.

    (а)\[\begin{split} (a)&\; (\textcolor{blue}{0}, \textcolor{red}{-3}) \qquad \qquad \quad \; (b)\; (\textcolor{blue}{3}, \textcolor{red}{3}) \qquad \qquad \qquad \quad (c)\; (\textcolor{blue}{2}, \textcolor{red}{-3}) \qquad \qquad \qquad \quad (d)\; (\textcolor{blue}{-1}, \textcolor{red}{-5}) \\ y &= 2x - 3 \qquad \qquad \quad y = 2x - 3 \qquad \qquad \qquad \; y = 2x - 3 \qquad \qquad \qquad \; \; \; y = 2x - 3 \\ \textcolor{red}{-3} &\stackrel{?}{=} 2(\textcolor{blue}{0}) - 3 \qquad \qquad \; \textcolor{red}{3} \stackrel{?}{=} 2(\textcolor{blue}{3}) - 3 \qquad \qquad \; \textcolor{red}{-3} \stackrel{?}{=} 2(\textcolor{blue}{2}) - 3 \qquad \qquad \; \; \; \textcolor{red}{-5} \stackrel{?}{=} 2(\textcolor{blue}{-1}) - 3 \\ -3 &= -3\; \checkmark \qquad \qquad \quad \; \; 3 = 3\; \checkmark \qquad \qquad \qquad -3 \neq 1 \qquad \qquad \qquad \qquad -5 = -5\; \checkmark \\ (0, -3)\;& is\; a\; solution \ldotp \quad (3, 3)\; is\; a\; solution \ldotp \qquad (2, -3)\; is\; not\; a\; solution \ldotp \qquad (-1, -5)\; is\; a\; solution \ldotp \end{split}\]

    (б) Побудуйте точки A: (0, − 3) B: (3, 3) C: (2, − 3) і D: (− 1, − 5). Точки (0, − 3), (3, 3) і (− 1, − 5) знаходяться на лінії y = 2x − 3, а точка (2, − 3) відсутня на лінії.

    ...

    Точки, які є розв'язками y = 2x − 3, знаходяться на прямій, але точка, яка не є розв'язком, не знаходиться на прямій.

    Вправа\(\PageIndex{1}\):

    Наведено графік y = 3x − 1. Для кожної впорядкованої пари вирішуйте (а) чи є впорядкована пара рішенням рівняння? (б) це точка на лінії?

    ...

    1. (0, − 1)
    2. (2, 2)
    3. (3, − 1)
    4. (− 1, − 4)
    Відповідь 1.

    а. так, б. ні

    Відповідь 2.

    а. ні, б. ні

    Відповідь 3.

    а. ні, б. ні

    Відповідь 4.

    а. так, б. так

    Графік лінійного рівняння шляхом побудови точок

    Існує кілька методів, які можуть бути використані для побудови графіка лінійного рівняння. Метод, який ми використовували на початку цього розділу для графування, називається точками побудови, або Метод точкового побудови.

    Давайте проведемо графік рівняння y = 2x+ 1 шляхом побудови точок. Почнемо з пошуку трьох точок, які є розв'язками рівняння. Ми можемо вибрати будь-яке значення для х або у, а потім вирішити для іншої змінної.

    Оскільки y ізольовано в лівій частині рівняння, то простіше вибрати значення для x, для цього прикладу ми будемо використовувати 0, 1 і -2 для x. Підставляємо кожне значення x в рівняння і вирішуємо для y.

    На малюнку показано три алгебраїчні заміни в рівняння. Перша заміна для x = -2, причому -2 показані синім кольором. Наступний рядок y = 2 х + 1. Наступний рядок y = 2 відкриті дужки -2, показані синім кольором, закриті дужки, + 1. Наступний рядок y = - 4 + 1. Наступний рядок y = -3. Останній рядок - «впорядкована пара -2, -3». Друга заміна для x = 0, при цьому 0 показано синім кольором. Наступний рядок y = 2 х + 1. Наступний рядок y = 2 відкриті дужки 0, показані синім кольором, закриті дужки, + 1. Наступний рядок y = 0 + 1. Наступний рядок y = 1. Останній рядок - «впорядкована пара 0, 2». Третя заміна призначена для x = 1, причому 1 показана синім кольором. Наступний рядок y = 2 х + 1. Наступний рядок y = 2 відкриті дужки 1, показані синім кольором, закриті дужки, + 1. Наступний рядок y = 2 + 1. Наступний рядок y = 3. Останній рядок - «впорядкована пара -1, 3».

    Ми можемо організувати рішення в таблиці. Див\(\PageIndex{1}\). Таблицю.

    Таблиця\(\PageIndex{1}\)
    у = 2х+ 1
    х у (х, у)
    0 1 (0, 1)
    1 3 (1, 3)
    -2 -3 (-2, -3)

    Тепер відкладаємо точки на прямокутну систему координат. Перевірте, щоб точки вибудовувалися. Якби вони не вишикувалися в чергу, це означало б, що ми помилилися і повинні перевірити ще раз всю нашу роботу. Див\(\PageIndex{2}\). Малюнок.

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -7 до 7. Показані три мічені точки: «впорядкована пара -2, -3», «впорядкована пара 0, 1» та впорядкована пара 1, 3».

    Малюнок\(\PageIndex{2}\)

    Проведіть лінію через три точки. Продовжити лінію, щоб заповнити сітку і поставити стрілки на обох кінцях лінії. Лінія - графік y = 2x + 1.

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -7 до 7. Лінія проходить через три мічені точки: «впорядкована пара -2, -3», «впорядкована пара 0, 1» та впорядкована пара 1, 3».

    Малюнок\(\PageIndex{3}\)

    ЯК: ГРАФІК ЛІНІЙНОГО РІВНЯННЯ ШЛЯХОМ ПОБУДОВИ ТОЧОК

    Крок 1. Знайдіть три точки, координати яких є розв'язками рівняння. Організуйте їх у вигляді таблиці.

    Крок 2. Помістіть точки на прямокутній системі координат. Перевірте, щоб точки вибудовувалися. Якщо їх немає, уважно перевірте свою роботу.

    Крок 3. Проведіть лінію через точки. Продовжити лінію, щоб заповнити сітку і поставити стрілки на обох кінцях лінії.

    Це правда, що для визначення лінії потрібно лише дві точки, але це хороша звичка використовувати три точки. Якщо ви намалюєте лише дві точки, і одна з них невірна, ви все одно можете провести лінію, але вона не буде представляти розв'язки рівняння. Це буде неправильна лінія. Якщо використовувати три точки, а одна невірна, точки не будуть вибудовуватися. Це говорить вам про те, що щось не так, і вам потрібно перевірити свою роботу. Див\(\PageIndex{4}\). Малюнок.

    Є дві фігури. На малюнку a показані три точки, які всі містяться на прямій лінії. Є лінія зі стрілками, яка пройшла через три точки. На малюнку b показані 3 точки, які не всі розташовані по прямій лінії.

    Малюнок\(\PageIndex{4}\) - Подивіться на різницю між (a) і (b). Всі три точки в (а) вирівнюються так що ми можемо провести одну лінію через них. Три точки в (b) не шикуються. Ми не можемо провести одну пряму лінію через усі три точки.

    Приклад\(\PageIndex{2}\):

    Графік рівняння y = −3x.

    Рішення

    Знайдіть три точки, які є розв'язками рівняння. Простіше вибрати значення для x і вирішити для y. Ви розумієте чому?

    На малюнку показано три алгебраїчні заміни в рівняння. Перша заміна призначена для x = 0, при цьому 0 показано синім кольором. Наступний рядок y = -3 x Наступний рядок y = -3 відкриті дужки 0, показані синіми, закритими дужками. Наступний рядок y = 0. Останній рядок - «впорядкована пара 0, 0». Друга заміна - для x = 1, при цьому 0 показано синім кольором. Наступний рядок y = -3 x Наступний рядок y = -3 відкриті дужки 1, показані синіми, закритими дужками. Наступний рядок y = -3. Останній рядок - «впорядкована пара 1, -3». Третя заміна - для x = -2, причому -2 показано синім кольором. Наступний рядок y = -3 x Наступний рядок y = -3 відкриті дужки -2, показані синіми, закритими дужками. Наступний рядок y = 6. Останній рядок - «впорядкована пара -2, 6».

    Перерахуйте пункти в таблиці.

    y = −3х
    х у (х, у)
    0 0 (0, 0)
    1 -3 (1, -3)
    -2 6 (-2, 6)

    Намалюйте точки, перевірте, щоб вони вишикувалися, і намалюйте лінію, як показано на малюнку.

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -7 до 7. Лінія проходить через три мічені точки: «впорядкована пара -2, 6», «впорядкована пара 0, 0» та впорядкована пара 1, -3». Рядок маркується y = -3 x.

    Вправа\(\PageIndex{2}\):

    Графік рівняння шляхом побудови точок: y = −4x.

    Відповідь

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -12 до 12. Через точки «впорядкована пара 0, 0» і «впорядкована пара 4, -4» проходить лінія.
    Вправа\(\PageIndex{3}\):

    Графік рівняння шляхом побудови точок: y = x.

    Відповідь

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -12 до 12. Через точки «впорядкована пара 0, 0» і «впорядкована пара 4, 4» проходить лінія.

    Коли рівняння містить дріб як коефіцієнт x, ми можемо замінити будь-яке число на x. Але математика буде простішою, якщо ми зробимо «хороший» вибір значень x. Таким чином ми уникнемо відповідей на дріб, які важко точно відображати.

    Приклад\(\PageIndex{3}\):

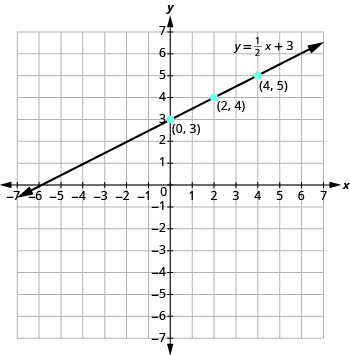
    Графік рівняння y =\(\dfrac{1}{2}\) x + 3.

    Рішення

    Знайдіть три точки, які є розв'язками рівняння. Оскільки це рівняння має дріб\(\dfrac{1}{2}\) як коефіцієнт х, ми будемо вибирати значення х ретельно. Ми будемо використовувати нуль як один вибір і кратні 2 для інших варіантів.

    На малюнку показано три алгебраїчні заміни в рівняння. Перша заміна призначена для x = 0, при цьому 0 показано синім кольором. Наступний рядок y = 1 над 2 x + 3. Наступний рядок y = 1 над 2 відкритими дужками 0, показані синім кольором, закриті дужки, + 3. Наступний рядок y = 3. Останній рядок - «впорядкована пара 0, 3». Друга заміна - для x = 2, причому 2 показані синім кольором. Наступний рядок y = 1 над 2 x + 3. Наступний рядок y = 1 над 2 відкритими дужками 2, показані синім кольором, закриті дужки, + 3. Наступний рядок y = 4. Останній рядок - «впорядкована пара 2, 4». Третя заміна для x = 4, причому 4 показані синім кольором. Наступний рядок y = 1 над 2 x + 3. Наступний рядок y = 1 над 2 відкритими дужками 4, показані синім кольором, закриті дужки, + 3. Наступний рядок y = 5. Останній рядок - «впорядкована пара 4, 5».

    Окуляри наведені в таблиці.

    у =\(\dfrac{1}{2}\) х + 3
    \ (\ dfrac {1} {2}\) х + 3">х у (х, у)
    \ (\ dfrac {1} {2}\) х + 3">0 3 (0, 3)
    \ (\ dfrac {1} {2}\) х + 3">2 4 (2, 4)
    \ (\ dfrac {1} {2}\) х + 3">4 5 (4, 5)

    Намалюйте точки, перевірте, щоб вони вишикувалися, і намалюйте лінію, як показано на малюнку.

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -7 до 7. Лінія проходить через три мічені точки, «впорядкована пара 0, 3», «впорядкована пара 2, 4», і впорядкована пара 4, 5». Рядок маркується y = 1 над 2 x + 3.

    Вправа\(\PageIndex{4}\):

    Графік рівняння: y =\(\dfrac{1}{3}\) x − 1

    Відповідь

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -12 до 12. Через точки «впорядкована пара 0, -1» і «впорядкована пара 3, 0» проходить лінія.

    Вправа\(\PageIndex{5}\):

    Графік рівняння: y =\(\dfrac{1}{4}\) x + 2.

    Відповідь

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -12 до 12. Через точки «впорядкована пара 0, 2» і «впорядкована пара -4, 1» проходить лінія.

    Поки що всі рівняння, які ми намалювали, мали y задано через х, Тепер ми будемо графувати рівняння з x і y на тій же стороні.

    Приклад\(\PageIndex{4}\):

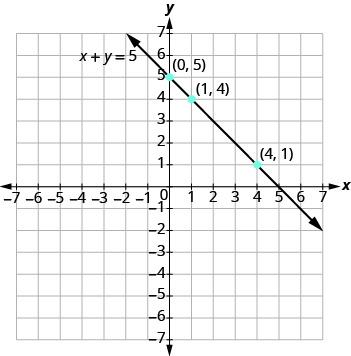
    Графік рівняння x + y = 5.

    Рішення

    Знайдіть три точки, які є розв'язками рівняння. Пам'ятайте, ви можете почати з будь-якого значення x або y.

    На малюнку показано три алгебраїчні заміни в рівняння. Перша заміна для x = 0, при цьому 0 показано синім кольором. Наступний рядок - x + y = 5. Наступний рядок дорівнює 0, показаний синім кольором + y = 5. Наступний рядок y = 5. Останній рядок - «впорядкована пара 0, 5». Друга заміна - для x = 1, причому 1 показана синім кольором. Наступний рядок - x + y = 5. Наступний рядок - 1, показаний синім кольором + y = 5. Наступний рядок y = 4. Останній рядок - «впорядкована пара 1, 4». Третя заміна для x = 4, причому 4 показані синім кольором. Наступний рядок - x + y = 5. Наступний рядок - 4, показаний синім кольором + y = 5. Наступний рядок y = 1. Останній рядок - «впорядкована пара 4, 1».

    Перерахуємо пункти в таблиці.

    х + у = 5
    х у (х, у)
    0 5 (0, 5)
    1 4 (1, 4)
    4 1 (4, 1)

    Потім намітьте точки, перевірте, щоб вони вишикувалися, і проведіть лінію.

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -7 до 7. Лінія проходить через три мічені точки, «впорядкована пара 0, 5», «впорядкована пара 1, 4», і впорядкована пара 4, 1». Рядок позначається x + y = 5.

    Вправа\(\PageIndex{6}\):

    Графік рівняння: x + y = −2.

    Відповідь

    Цей графік відповідей показує координатну площину x y. По осі x і y кожна проходить від -12 до 12. Показано рівняння x плюс y дорівнює -2. Через перехоплення проходить лінія з координатами 0, —2 та -2, 0.

    Вправа\(\PageIndex{7}\):

    Графік рівняння: x − y = 6.

    Відповідь

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -12 до 12. Через точки «впорядкована пара 6, 0» і «впорядкована пара 0, -6» проходить лінія.

    У попередньому прикладі три точки, які ми знайшли, було легко графувати. Але це не завжди так. Давайте подивимося, що відбувається в рівнянні 2x + y = 3. Якщо y дорівнює 0, яке значення x?

    \[\begin{split} 2x + y &= 3 \\ 2x + \textcolor{red}{0} &= 3 \\ 2x &= 3 \\ x &= \dfrac{3}{2} \end{split}\]

    Рішення - справа\(\left(\dfrac{3}{2}, 0\right)\). Ця точка має дріб для координати x. Хоча ми могли б графікувати цю точку, важко бути точним графіки дробів. Пам'ятайте, в прикладі y =\(\dfrac{1}{2}\) x + 3 ми ретельно вибирали значення для x, щоб взагалі не графувати дроби. Якщо вирішити рівняння 2x + y = 3 для y, легше буде знайти три рішення рівняння.

    \[\begin{split} 2x + y &= 3 \\ y &= -2x + 3 \end{split}\]

    Тепер ми можемо вибрати значення для х, які дадуть координати, які є цілими числами. Наведено розв'язки для x = 0, x = 1 та x = −1.

    y = −2х+ 3
    х у (х, у)
    0 3 (0, 3)
    1 1 (1, 1)
    -1 5 (-1, 5)

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -7 до 7. Лінія проходить через три мічені точки: «впорядкована пара -1, 5», «впорядкована пара 0, 3» та впорядкована пара 1, 1». Рядок маркується 2 х + y = 3.

    Приклад\(\PageIndex{5}\):

    Графік рівняння 3x + y = −1.

    Рішення

    Знайдіть три точки, які є розв'язками рівняння.

    Спочатку розв'яжіть рівняння для y.

    \[\begin{split} 3x + y &= −1 \\ y &= −3x − 1 \end{split}\]

    Ми дозволимо x дорівнювати 0, 1 та −1, щоб знайти три точки. Впорядковані пари наведені в таблиці. Намалюйте точки, перевірте, щоб вони вишикувалися, і проведіть лінію.

    y = −3x − 1
    х у (х, у)
    0 -1 (0, -1)
    1 -4 (1, -4)
    -1 2 (-1, 2)

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -7 до 7. Лінія проходить через три мічені точки: «впорядкована пара -1, 2», «впорядкована пара 0, -1» та впорядкована пара 1, -4». Рядок маркується 3 x + y = -1.

    Якщо ви можете вибрати будь-які три точки для графіка лінії, як ви дізнаєтесь, чи відповідає ваш графік тому, який показаний у відповідях у книзі? Якщо точки, де графіки перетинають осі x- та y, однакові, графіки збігаються.

    Вправа\(\PageIndex{8}\):

    Графік кожного рівняння: 2x + y = 2.

    Відповідь
    На графіку показана координатна площина x y. По осі x і y кожна проходить від -12 до 12. Лінія проходить через три мічені точки: «впорядкована пара -1, 4», «впорядкована пара 0, 2» та впорядкована пара 1, 0».
    Вправа\(\PageIndex{9}\):

    Графік кожного рівняння: 4x + y = −3.

    Відповідь

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -12 до 12. Через точки «впорядкована пара -2, 5» і «впорядкована пара 0, -3» проходить лінія.

    Дописувачі та атрибуція