Skip to main content
LibreTexts - Ukrayinska

10.7: Розділити мономи (частина 2)

  1. Last updated
  2. Save as PDF
  • Page ID
    57902

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Спрощення виразів за допомогою застосування декількох властивостей

    Тепер ми підсумуємо всі властивості експонентів, щоб вони всі разом посилатися, оскільки ми спрощуємо вирази, використовуючи кілька властивостей. Зверніть увагу, що тепер вони визначені для цілих числових показників.

    Резюме властивостей експоненти

    Якщо a, b - дійсні числа, а m, n - цілі числа, то

    Властивість продукту \(a^m • a^n = a^{m + n}\)
    Власне майно \((a^m)^n = a^{m • n}\)
    Продукт у власність влади \((ab)^m = a^mb^m\)
    Частота власності \(\dfrac{a^{m}}{a^{n}} = a^{m − n},\quad a ≠ 0,\, m > n\)
      \(\dfrac{a^{m}}{a^{n}} = \dfrac{1}{a^{n-m}}, \quad a ≠ 0, \,n > m\)
    Нульовий показник властивості \(a^0 = 1, \quad a ≠ 0\)
    Коефіцієнт до власності влади \(\left(\dfrac{a}{b}\right)^{m} = \dfrac{a^{m}}{b^{m}}, b ≠ 0\)
    Приклад\(\PageIndex{8}\):

    Спростити:\(\dfrac{(x^{2})^{3}}{x^{5}}\).

    Рішення

    Помножте показники в чисельнику, використовуючи властивість Power. \(\dfrac{x^{6}}{x^{5}} \label{10.4.46}\)
    Відніміть показники. \(x \label{10.4.47}\)
    Вправа\(\PageIndex{15}\):

    Спростити:\(\dfrac{(a^{4})^{5}}{a^{9}}\).

    Відповідь

    \(a^{11}\)

    Вправа\(\PageIndex{16}\):

    Спростити:\(\dfrac{(b^{5})^{6}}{b^{11}}\).

    Відповідь

    \(b^{19}\)

    Приклад\(\PageIndex{9}\):

    Спростити:\(\dfrac{(m^{8})}{(m^{2})^{4}}\).

    Рішення

    Помножте показники в чисельнику, використовуючи властивість Power. \(\dfrac{m^{8}}{m^{8}} \label{10.4.48}\)
    Відніміть показники. \(m^{0} \label{10.4.49}\)
    Властивість нульової потужності 1
    Вправа\(\PageIndex{17}\):

    Спростити:\(\dfrac{(k^{11}}{(k^{3})^{3}}\).

    Відповідь

    \(k^2\)

    Вправа\(\PageIndex{18}\):

    Спростити:\(\dfrac{(d^{23}}{(d^{4})^{6}}\).

    Відповідь

    \(\frac{1}{d}\)

    Приклад\(\PageIndex{10}\):

    Спростити:\(\left(\dfrac{x^{7}}{x^{3}}\right)^{2}\).

    Рішення

    Пам'ятайте, що дужки приходять перед показниками, і основи однакові, тому ми можемо спростити всередині дужок. Відніміть показники. \((x^{7-3})^{2} \label{10.4.50}\)
    Спростити. \((x^{4})^{2} \label{10.4.51}\)
    Помножте показники. \(x^{8} \label{10.4.52}\)
    Вправа\(\PageIndex{19}\):

    Спростити:\(\left(\dfrac{f^{14}}{f^{8}}\right)^{2}\).

    Відповідь

    \(f^{12}\)

    Вправа\(\PageIndex{20}\):

    Спростити:\(\left(\dfrac{b^{6}}{b^{11}}\right)^{2}\).

    Відповідь

    \(\frac{1}{b^{10}}\)

    Приклад\(\PageIndex{11}\):

    Спростити:\(\left(\dfrac{p^{2}}{q^{5}}\right)^{3}\).

    Рішення

    Тут ми не можемо спочатку спростити всередині дужок, оскільки основи не однакові.

    Підніміть чисельник і знаменник до третього ступеня за допомогою коефіцієнта до властивості влади,\(\left(\dfrac{a}{b}\right)^{m} = \dfrac{a^{m}}{b^{m}}\) \(\dfrac{(p^{2})^{3}}{(q^{5})^{3}} \label{10.4.53}\)
    Використовуйте властивість Потужність, (a m) n = a m • n. \(\dfrac{p^{6}}{q^{15}} \label{10.4.54}\)
    Вправа\(\PageIndex{21}\):

    Спростити:\(\left(\dfrac{m^{3}}{n^{8}}\right)^{5}\).

    Відповідь

    \(\frac{m^{15}}{n^{40}}\)

    Вправа\(\PageIndex{22}\):

    Спростити:\(\left(\dfrac{t^{10}}{u^{7}}\right)^{2}\).

    Відповідь

    \(\frac{t^{20}}{u^{14}}\)

    Приклад\(\PageIndex{12}\):

    Спростити:\(\left(\dfrac{2x^{3}}{3y}\right)^{4}\).

    Рішення

    Підніміть чисельник і знаменник до четвертого ступеня за допомогою коефіцієнта до властивості влади. \(\dfrac{(2x^{3})^{4}}{(3y)^{4}} \label{10.4.55}\)
    Підніміть кожен фактор до четвертої влади, використовуючи владу до властивості влади. \(\dfrac{2^{4} (x^{3})^{4}}{3^{4} y^{4}} \label{10.4.56}\)
    Скористайтеся властивістю Power і спрощуйте. \(\dfrac{16x^{12}}{81y^{4}} \label{10.4.57}\)
    Вправа\(\PageIndex{23}\):

    Спростити:\(\left(\dfrac{5b}{9c^{3}}\right)^{2}\).

    Відповідь

    \(\frac{25b^2}{81c^6}\)

    Вправа\(\PageIndex{24}\):

    Спростити:\(\left(\dfrac{4p^{4}}{7q^{5}}\right)^{3}\).

    Відповідь

    \(\frac{64p^{12}}{343q^{15}}\)

    Приклад\(\PageIndex{13}\):

    Спростити:\(\dfrac{(y^{2})^{3} (y^{2})^{4}}{(y^{5})^{4}}\).

    Рішення

    Використовуйте властивість Power. \(\dfrac{(y^{6})(y^{8})}{y^{20}} \label{10.4.58}\)
    Додайте показники в чисельнику, використовуючи Product Property. \(\dfrac{y^{14}}{y^{20}} \label{10.4.59}\)
    Використовуйте властивість частки. \(\dfrac{1}{y^{6}} \label{10.4.60}\)
    Вправа\(\PageIndex{25}\)

    Спростити:\(\dfrac{(y^{4})^{4} (y^{3})^{5}}{(y^{7})^{6}}\).

    Відповідь

    \(\frac{1}{y^{11}}\)

    Вправа\(\PageIndex{26}\)

    Спростити:\(\dfrac{(3x^{4})^{2} (x^{3})^{4}}{(x^{5})^{3}}\).

    Відповідь

    \(9x^5\)

    Розділити мономи

    Зараз ми побачили всі властивості експонентів. Ми будемо використовувати їх, щоб розділити мономи. Пізніше ви будете використовувати їх для поділу многочленів.

    Приклад\(\PageIndex{14}\):

    Знайдіть коефіцієнт: 56x 5 ÷ 7x 2.

    Рішення

    Перепишіть як дріб. \(\dfrac{56x^{5}}{7x^{2}} \label{10.4.61}\)
    Використовуйте множення дробу, щоб відокремити числову частину від змінної частини. \(\dfrac{56}{7} \cdot \dfrac{x^{5}}{x^{2}} \label{10.4.62}\)
    Використовуйте властивість частки. \(8x^{3} \label{10.4.63}\)
    Вправа\(\PageIndex{27}\):

    Знайдіть коефіцієнт: 63x 8 ÷ 9x 4.

    Відповідь

    \(7x^4\)

    Вправа\(\PageIndex{28}\):

    Знайдіть коефіцієнт: 96y 11 ÷ 6y 8.

    Відповідь

    \(16y^3\)

    Коли ми ділимо мономіали з більш ніж однією змінною, ми пишемо один дріб для кожної змінної.

    Приклад\(\PageIndex{15}\):

    Знайдіть частку:\(\dfrac{42x^{2} y^{3}}{−7xy^{5}}\).

    Рішення

    Використовуйте множення дробів. \(\dfrac{42}{-7} \cdot \dfrac{x^{2}}{x} \cdot \dfrac{y^{3}}{y^{5}} \label{10.4.64}\)
    Спростіть і використовувати властивість частки. \(-6 \cdot x \cdot \dfrac{1}{y^{2}} \label{10.4.65}\)
    Помножити. \(- \dfrac{6x}{y^{2}} \label{10.4.66}\)
    Вправа\(\PageIndex{29}\):

    Знайдіть частку:\(\dfrac{-84x^{8} y^{3}}{7x^{10} y^{2}}\).

    Відповідь

    \(-\frac{12y}{x^2}\)

    Вправа\(\PageIndex{30}\):

    Знайдіть частку:\(\dfrac{-72a^{4} b^{5}}{−8a^{9} b^{5}}\).

    Відповідь

    \(\frac{9}{a^5}\)

    Приклад\(\PageIndex{16}\):

    Знайдіть частку:\(\dfrac{24a^{5} b^{3}}{48ab^{4}}\).

    Рішення

    Використовуйте множення дробів. \(\dfrac{24}{48} \cdot \dfrac{a^{5}}{a} \cdot \dfrac{b^{3}}{b^{4}} \label{10.4.67}\)
    Спростіть і використовувати властивість частки. \(\dfrac{1}{2} \cdot a^{4} \cdot \dfrac{1}{b} \label{10.4.68}\)
    Помножити. \(\dfrac{a^{4}}{2b} \label{10.4.69}\)
    Вправа\(\PageIndex{31}\):

    Знайдіть частку:\(\dfrac{16a^{7} b^{6}}{24ab^{8}}\).

    Відповідь

    \(\frac{2a^6}{3b^2}\)

    Вправа\(\PageIndex{32}\):

    Знайдіть частку:\(\dfrac{27p^{4} q^{7}}{-45p^{12} q}\).

    Відповідь

    \(-\frac{3q^6}{5p^8}\)

    Після того, як ви ознайомитеся з процесом і практикуєте його крок за кроком кілька разів, ви можете спростити частку за один крок.

    Приклад\(\PageIndex{17}\):

    Знайдіть частку:\(\dfrac{14x^{7} y^{12}}{21x^{11} y^{6}}\).

    Рішення

    Спростіть і використовувати властивість частки. \(\dfrac{2y^{6}}{3x^{4}} \label{10.4.70}\)

    Будьте дуже обережні, щоб спростити,\(\dfrac{14}{21}\) розділивши загальний коефіцієнт, і спростити змінні, віднімаючи їх показники.

    Вправа\(\PageIndex{33}\):

    Знайдіть частку:\(\dfrac{28x^{5} y^{14}}{49x^{9} y^{12}}\).

    Відповідь

    \(\frac{4y^2}{7x^4}\)

    Вправа\(\PageIndex{34}\):

    Знайдіть частку:\(\dfrac{30m^{5} n^{11}}{48m^{10} n^{14}}\).

    Відповідь

    \(\frac{5}{8m^5 n^3}\)

    У всіх прикладах досі не було роботи в чисельнику або знаменнику перед спрощенням дробу. У наступному прикладі ми спочатку знайдемо добуток двох мономов у чисельнику, перш ніж спростити дріб.

    Приклад\(\PageIndex{18}\):

    Знайдіть частку:\(\dfrac{(3x^{3} y^{2})(10x^{2} y^{3})}{6x^{4} y^{5}}\).

    Рішення

    Пам'ятайте, що смужка дробу є символом угруповання. Спочатку ми спростимо чисельник.

    Спростити чисельник. \(\dfrac{30x^{5} y^{5}}{6x^{4} y^{5}} \label{10.4.71}\)
    Спростіть, використовуючи правило частки. \(5x \label{10.4.72}\)
    Вправа\(\PageIndex{35}\):

    Знайдіть частку:\(\dfrac{(3x^{4} y^{5})(8x^{2} y^{5})}{12x^{5} y^{8}}\).

    Відповідь

    \(2xy^2\)

    Вправа\(\PageIndex{36}\):

    Знайдіть частку:\(\dfrac{(-6a^{6} b^{9})(-8a^{5} b^{8})}{-12a^{10} b^{12}}\).

    Відповідь

    \(-4ab^5\)

    ДОСТУП ДО ДОДАТКОВИХ ОНЛАЙН-РЕСУРСІВ

    Спрощення частки

    Нульовий показник

    Частота Правило

    Поліноміальний поділ

    Поліноміальний поділ 2

    Практика робить досконалим

    Спрощення виразів за допомогою коефіцієнтної властивості експонентів

    У наступних вправах спростити.

    1. \(\dfrac{4^{8}}{4^{2}}\)
    2. \(\dfrac{3^{12}}{3^{4}}\)
    3. \(\dfrac{x^{12}}{x^{3}}\)
    4. \(\dfrac{u^{9}}{u^{3}}\)
    5. \(\dfrac{r^{5}}{r}\)
    6. \(\dfrac{y^{4}}{y}\)
    7. \(\dfrac{y^{4}}{y^{20}}\)
    8. \(\dfrac{x^{10}}{x^{30}}\)
    9. \(\dfrac{10^{3}}{10^{15}}\)
    10. \(\dfrac{r^{2}}{r^{8}}\)
    11. \(\dfrac{a}{a^{9}}\)
    12. \(\dfrac{2}{2^{5}}\)

    Спрощення виразів з нульовими показниками

    У наступних вправах спростити.

    1. 5 0
    2. 10 0
    3. a 0
    4. х 0
    5. −7 0
    6. −4 0
    7. (а) (10р) 0 (б) 10р 0
    8. (а) (3а) 0 (б) 3а 0
    9. (а) (−27х 5 у) 0 (б) −27х 5 у 0
    10. (а) (−92y 8 з) 0 (б) −92y 8 з 0
    11. (а) 15 0 (б) 15 1
    12. (a) −6 0 (b) −6 1
    13. 2 • х 0 + 5 • у 0
    14. 8 • м 0 − 4 • n 0

    Спрощення виразів за допомогою коефіцієнта до властивості влади

    У наступних вправах спростити.

    1. \(\left(\dfrac{3}{2}\right)^{5}\)
    2. \(\left(\dfrac{4}{5}\right)^{3}\)
    3. \(\left(\dfrac{m}{6}\right)^{3}\)
    4. \(\left(\dfrac{p}{2}\right)^{5}\)
    5. \(\left(\dfrac{x}{y}\right)^{10}\)
    6. \(\left(\dfrac{a}{b}\right)^{8}\)
    7. \(\left(\dfrac{a}{3b}\right)^{2}\)
    8. \(\left(\dfrac{2x}{y}\right)^{4}\)

    Спрощення виразів за допомогою застосування декількох властивостей

    У наступних вправах спростити.

    1. \(\dfrac{(x^{2})^{4}}{x^{5}}\)
    2. \(\dfrac{(y^{4})^{3}}{y^{7}}\)
    3. \(\dfrac{(u^{3})^{4}}{u^{10}}\)
    4. \(\dfrac{(y^{2})^{5}}{y^{6}}\)
    5. \(\dfrac{y^{8}}{(y^{5})^{2}}\)
    6. \(\dfrac{p^{11}}{(p^{5})^{3}}\)
    7. \(\dfrac{r^{5}}{(r^{4} \cdot r}\)
    8. \(\dfrac{a^{3} \cdot a^{4}}{(a^{7}}\)
    9. \(\left(\dfrac{x^{2}}{x^{8}}\right)^{3}\)
    10. \(\left(\dfrac{u}{u^{10}}\right)^{2}\)
    11. \(\left(\dfrac{a^{4} \cdot a^{6}}{a^{3}}\right)^{2}\)
    12. \(\left(\dfrac{x^{3 \cdot x^{8}}}{x^{4}}\right)^{3}\)
    13. \(\dfrac{(y^{3})^{5}}{(y^{4})^{3}}\)
    14. \(\dfrac{(z^{6})^{2}}{(z^{2})^{4}}\)
    15. \(\dfrac{(x^{3})^{6}}{(x^{4})^{7}}\)
    16. \(\dfrac{(x^{4})^{8}}{(x^{5})^{7}}\)
    17. \(\left(\dfrac{2r^{3}}{5s}\right)^{4}\)
    18. \(\left(\dfrac{3m^{2}}{4n}\right)^{3}\)
    19. \(\left(\dfrac{3y^{2} \cdot y^{5}}{y^{15} \cdot y^{8}}\right)^{0}\)
    20. \(\left(\dfrac{15z^{4} \cdot z^{9}}{0.3z^{2}}\right)^{0}\)
    21. \(\dfrac{(r^{2})^{5} (r^{4})^{2}}{(r^{3})^{7}}\)
    22. \(\dfrac{(p^{4})^{2} (p^{3})^{5}}{(p^{2})^{9}}\)
    23. \(\dfrac{(3x^{4})^{3} (2x^{3})^{2}}{(6x^{5})^{2}}\)
    24. \(\dfrac{(-2y^{3})^{4} (3y^{4})^{2}}{(-6y^{3})^{2}}\)

    Розділити мономи

    У наступних вправах розділіть мономи.

    1. 48б 8 ÷ 6б 2
    2. 42а 14 ÷ 6а 2
    3. 36x 3 ÷ (−2х 9)
    4. 20u 8 ÷ (−4у 6)
    5. \(\dfrac{18x^{3}}{9x^{2}}\)
    6. \(\dfrac{36y^{9}}{4y^{7}}\)
    7. \(\dfrac{-35x^{7}}{-42x^{13}}\)
    8. \(\dfrac{18x^{5}}{-27x^{9}}\)
    9. \(\dfrac{18r^{5} s}{3r^{3} s^{9}}\)
    10. \(\dfrac{24p^{7} q}{6p^{2} q^{5}}\)
    11. \(\dfrac{8mn^{10}}{64mn^{4}}\)
    12. \(\dfrac{10a^{4} b}{50a^{2} b^{6}}\)
    13. \(\dfrac{-12x^{4} y^{9}}{15x^{6} y^{3}}\)
    14. \(\dfrac{48x^{11} y^{9} z^{3}}{36x^{6} y^{8} z^{5}}\)
    15. \(\dfrac{64x^{5} y^{9} z^{7}}{48x^{7} y^{12} z^{6}}\)
    16. \(\dfrac{(10u^{2} v)(4u^{3} v^{6})}{5u^{9} v^{2}}\)
    17. \(\dfrac{(6m^{2} n)(5m^{4} n^{3})}{3m^{10} n^{2}}\)
    18. \(\dfrac{(6a^{4} b^{3})(4ab^{5})}{(12a^{8} b)(a^{3} b)}\)
    19. \(\dfrac{(4u^{5} v^{4})(15u^{8} v)}{(12u^{3} v)(u^{6} v)}\)

    Змішана практика

    1. (а) 24а 5 + 2а 5 (б) 24а 5 − 2а 5 (с) 24а 5 • 2а 5 (г) 24а 5 ÷ 2а 5
    2. (а) 15н 10 + 3н 10 (б) 15н 10 − 3н 10 (с) 15н 10 • 3н 10 (д) 15н 10 ÷ 3н 10
    3. (а) п 4 • п 6 (б) (п. 4) 6
    4. (а) q 5 • q 3 (б) (q 5) 3
    5. (а)\(\dfrac{ y^{3}}{y}\) (б)\(\dfrac{y}{y^{3}}\)
    6. (а)\(\dfrac{z^{6}}{z^{5}}\) (б)\(\dfrac{z^{5}}{z^{6}}\)
    7. (8х 5) (9х) ÷ 6х 3
    8. (4й 5) (12й 7) ÷ 8у 2
    9. \(\dfrac{27a^{7}}{3a^{3}} + \dfrac{54a^{9}}{9a^{5}}\)
    10. \(\dfrac{32c^{11}}{4c^{5}} + \dfrac{42c^{9}}{6c^{3}}\)
    11. \(\dfrac{32y^{5}}{8y^{2}} - \dfrac{60y^{10}}{5y^{7}}\)
    12. \(\dfrac{48x^{6}}{6x^{4}} - \dfrac{35x^{9}}{7x^{7}}\)
    13. \(\dfrac{63r^{6} s^{3}}{9r^{4} s^{2}} - \dfrac{72r^{2} s^{2}}{6s}\)
    14. \(\dfrac{56y^{4} z^{5}}{7y^{3} z^{3}} - \dfrac{45y^{2} z^{2}}{5y}\)

    Щоденна математика

    1. Пам'ять Один мегабайт становить приблизно 10 6 байт. Один гігабайт дорівнює приблизно 10 9 байтам. Скільки мегабайт в одному гігабайті?
    2. Пам'ять Один мегабайт становить приблизно 10 6 байт. Один терабайт дорівнює приблизно 10 12 байтам. Скільки мегабайт в одному терабайті?

    Письмові вправи

    1. Вік вважає, що частка\(\dfrac{x^{20}}{x^{4}}\) спрощується до x 5. Що не так з його міркуваннями?
    2. Mai спрощує частку\(\dfrac{y^{3}}{y}\) шляхом написання\(\dfrac{y^{3}}{y}\) = 3. Що не так з її міркуваннями?
    3. Коли Dimple спростила −3 0 та (−3) 0, вона отримала таку ж відповідь. Поясніть, як правильне використання Порядку операцій дає різні відповіді.
    4. Роксі вважає, що 0 спрощує до 0. Що б ви сказали, щоб переконати Роксі, що вона помиляється?

    Самостійна перевірка

    (а) Після виконання вправ використовуйте цей контрольний список, щоб оцінити своє володіння цілями цього розділу.

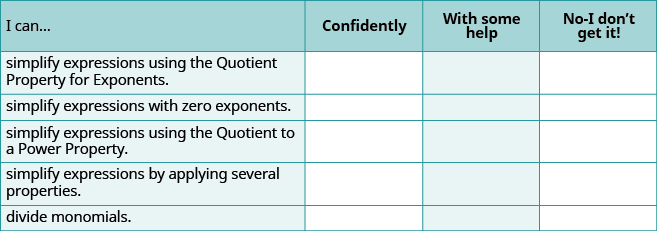
    CNX_BMath_Figure_AppB_063.jpg

    (b) За шкалою 1—10, як би ви оцінили своє володіння цим розділом у світлі ваших відповідей на контрольний список? Як ви можете це покращити?

    Автори та атрибуція