10.1: Додавання та віднімання поліномів

Цілі навчання

• Визначте многочлени, мономи, біноми та тріноми
• Визначаємо ступінь многочленів
• Додавання та віднімання мономи
• Додавання та віднімання многочленів
• Оцінити многочлен для заданого значення

будьте готові!

Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

1. Спрощення: 8х+ 3x. Якщо ви пропустили цю проблему, перегляньте приклад 2.3.10.
2. Відніміть: (5n + 8) − (2n − 1). Якщо ви пропустили цю проблему, перегляньте приклад 7.4.13.
3. Оцініть: 4y ², коли y = 5 Якщо ви пропустили цю проблему, перегляньте приклад 2.3.6.

Визначте многочлени, мономи, біноми та триноми

У розділі «Оцінювати», «Спростити» і «Перекласти вирази» ви дізналися, що термін є константою або добутком константи і однієї або декількох змінних. Коли вона має форму ax ^m, де a - константа, а m - ціле число, його називають мономіальним. Мономіал, або сума і/або різниця мономов, називається поліном.

Визначення: Поліноми

многочлен — мономіал, або два або більше мономи, об'єднані додаванням або відніманням

мономіальний — многочлен з рівно одним членом

binomial — многочлен з рівно двома долями

trinomial — многочлен з рівно трьома доходами

Зверніть увагу на коріння:

• полі - означає багато
• моно - означає один
• bi - означає два
• три - означає три

Ось кілька прикладів многочленів:

многочлен	б + 1	4 роки × ^2 − 7 років + 2	5х ^5 − 4х ^4 + х ^3 + 8х ^2 − 9х+ 1
Мономіальний	5	4б ^2	-9х ^3
Біноміальний	3а - 7	у ^2 - 9	17х ^3 + 14х ^2
Тримінал	х ^2 - 5х+ 6	4 р ^2 - 7й + 2	5а ^4 - 3а ^3 + а

Зверніть увагу, що кожен мономіальний, біноміальний і триноміальний також є поліномом. Вони є особливими членами сімейства поліномів і тому мають особливі назви. Ми використовуємо слова «мономіальний», «біноміальний» та «триноміальний» при зверненні до цих спеціальних поліномів і просто називаємо всі інші «поліноми».

Приклад\(\PageIndex{1}\):

Визначте, чи є кожен многочлен мономіальним, біноміальним, тріноміальним чи іншим поліномом: (a) 8x ² − 7x − 9 (b) −5a ⁴ (c) x ⁴ − 7x ³ − 6x ² + 5x 2 (d) 11 − 4y ³ (e) n

Рішення

многочлен	Кількість термінів	Тип
(а) 8х ^2 − 7х − 9	3	Тримінал
(б) −5а ^4	1	Мономіальний
(с) х ^4 − 7х ^3 − 6х ^2 + 5х+ 2	5	многочлен
(d) 11 − 4 роки ^3	2	Біноміальний
(д) н	1	Мономіальний

Вправа\(\PageIndex{1}\):

Визначте, чи є кожен многочлен мономіальним, біноміальним, триноміальним або іншим поліномом. (a) z (b) 2х ³ − 4х ² − х − 8 (с) 6х ² − 4х + 1 (г) 9 − 4й ² (е) 3х ⁷

Відповідь на

мономіальний

Відповідь б

многочлен

Відповідь c

тріпомінал

Відповідь d

біноміальних

Відповідь e

мономіальний

Вправа\(\PageIndex{2}\):

Визначте, чи є кожен многочлен мономіальним, біноміальним, триноміальним або іншим поліномом. (a) y ³ − 8 (b) 9x ³ − 5x ² − x (c) x ⁴ − 3x ² − 4x − 7 (d) −y ⁴ (е) ш

Відповідь на

біноміальних

Відповідь б

тріпомінал

Відповідь c

многочлен

Відповідь d

мономіальний

Відповідь e

мономіальний

Визначаємо ступінь многочленів

У цьому розділі ми будемо працювати з поліномами, які мають лише одну змінну в кожному члені. Ступінь многочлена і ступінь його членів визначаються показниками змінної.

Мономіал, який не має змінної, просто константа, - це особливий випадок. Ступінь константи дорівнює 0 —вона не має змінної.

Визначення: Ступінь многочлена

Ступінь терміна - це показник його змінної.

Ступінь константи дорівнює 0.

Ступінь многочлена - найвища ступінь з усіх його членів.

Давайте подивимося, як це працює, подивившись на кілька поліномів. Ми будемо приймати це крок за кроком, починаючи з мономов, а потім прогресуючи до поліномів з більшою кількістю термінів.

Пам'ятайте: Будь-яка база, написана без показника, має на увазі показник 1.

Приклад\(\PageIndex{2}\):

Знайти ступінь наступних многочленів: (a) 4x (b) 3x ³ − 5x + 7 (c) −11 (d) −6x ² + 9x − 3 (e) 8x + 2

Рішення

(а) 4х

Показник х дорівнює одиниці. x = x ^1

Ступінь дорівнює 1.

(б) 3х ³ − 5х+ 7

Найвищий ступінь з усіх термінів - 3.

Ступінь - 3.

(c) −11

Ступінь константи дорівнює 0.

Ступінь дорівнює 0.

(г) −6х ² + 9х − 3

Найвищий ступінь з усіх термінів - 2.

Ступінь - 2.

(е) 8х+ 2

Найвищий ступінь з усіх термінів - 1.

Ступінь дорівнює 1.

Вправа\(\PageIndex{3}\):

Знайти ступінь наступних многочленів: (a) −6y (b) 4x − 1 (c) 3x ⁴ + 4x ² − 8 (d) 2y ² + 3y + 9 (e) −18

Відповідь на

1

Відповідь б

1

Відповідь c

4

Відповідь d

2

Відповідь e

0

Вправа\(\PageIndex{4}\):

Знайти ступінь наступних многочленів: (a) 47 (b) 2x ^{2 − 8x + 2} (c) x ⁴ − 16 (d) y ⁵ − 5y ³ + y (e) 9a ^{3 3}

Відповідь на

0

Відповідь б

2

Відповідь c

4

Відповідь d

5

Відповідь e

3

Працювати з поліномами простіше, коли ви перераховуєте терміни в порядку спадання градусів. Коли многочлен пишеться таким чином, він, як кажуть, в стандартній формі. Подивіться назад на многочлени в прикладі 10.2. Зверніть увагу, що всі вони написані в стандартній формі. Отримайте звичку спочатку писати термін з вищим ступенем.

Додавання та віднімання мономи

У Мові алгебри ви спростили вирази, комбінуючи подібні терміни. Додавання та віднімання мономов - це те саме, що і комбінування подібних термінів. Подібні терміни повинні мати однакову змінну з однаковим показником. Нагадаємо, що при комбінуванні подібних термінів об'єднуються тільки коефіцієнти, а не показники.

Приклад\(\PageIndex{3}\):

Додайте: 17х ² + 6х ².

Рішення

Поєднуйте подібні терміни.

23х ^2

Вправа\(\PageIndex{5}\):

Додати: 12х ² + 5х ².

Відповідь

17х ²

Вправа\(\PageIndex{6}\):

Додати: −11у ² + 8у ².

Відповідь

-3й ²

Приклад\(\PageIndex{4}\):

Відніміть: 11n − (−8n).

Рішення

Поєднуйте подібні терміни.

19н

Вправа\(\PageIndex{7}\):

Відніміть: 9n − (−5n).

Відповідь

14н

Вправа\(\PageIndex{8}\):

Відніміть: −7a ³ − (−5a ³).

Відповідь

-2а ³

Приклад\(\PageIndex{5}\):

Спрощення: a ² + 4b ² − 7a ².

Рішення

Поєднуйте подібні терміни.

−6а ^2 + 4б ^2

Пам'ятайте, що −6a ² та 4b ² не схожі на терміни. Змінні не однакові.

Вправа\(\PageIndex{9}\):

Додайте: 3х ² + 3у ² − 5х ².

Відповідь

-2х ² + 3й ²

Вправа\(\PageIndex{10}\):

Додайте: 2а ² + б ² − 4а ².

Відповідь

-2а ² + б ²

Додавання та віднімання многочленів

Додавання та віднімання поліномів можна розглядати як просто додавання та віднімання подібних термінів. Шукайте подібні терміни - ті, у яких однакові змінні з однаковим показником. Комутативна власність дозволяє нам змінювати умови, щоб скласти подібні терміни разом. Також може бути корисно підкреслити, обвести або поле, як терміни.

Приклад\(\PageIndex{6}\):

Знайти суму: (4x ² − 5x + 1) + (3x ² − 8x − 9)

Рішення

Визначте подібні терміни.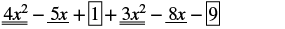
Переставляйте, щоб отримати подібні терміни разом.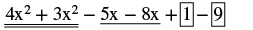
Поєднуйте подібні терміни.

Вправа\(\PageIndex{11}\):

Знайдіть суму: (3x ² − 2x + 8) + (x ² − 6x + 2).

Відповідь

4х ² - 8х + 10

Вправа\(\PageIndex{12}\):

Знайти суму: (7y ² + 4y − 6) + (4y ² + 5y + 1)

Відповідь

11 р ² + 9 років - 5

Дужки - це угруповання символів. Коли ми додаємо поліноми, як ми зробили в прикладі 10.6, ми можемо переписати вираз без дужок, а потім об'єднати як терміни. Але коли ми віднімаємо многочлени, ми повинні бути дуже обережними зі знаками.

Приклад\(\PageIndex{7}\):

Знайдіть різницю: (7u ² − 5u + 3) − (4u ² − 2).

Рішення

Поширюйте та ідентифікуйте подібні терміни.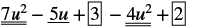
Перевпорядкувати умови.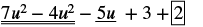
Поєднуйте подібні терміни.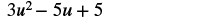

Вправа\(\PageIndex{13}\):

Знайдіть різницю: (6y ² + 3y − 1) − (3y ² − 4).

Відповідь

3й ² + 3й + 3

Вправа\(\PageIndex{14}\):

Знайдіть різницю: (8u ² − 7u − 2) − (5u ² − 6u − 4).

Відповідь

3у ² - у + 2

Приклад\(\PageIndex{8}\):

Відніміть: (м ² − 3м + 8) від (9м ² − 7м+ 4).

Рішення

Поширюйте та ідентифікуйте подібні терміни.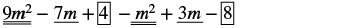
Перевпорядкувати умови.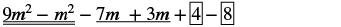
Поєднуйте подібні терміни.

Вправа\(\PageIndex{15}\):

Відніміть: (4n ² − 7n − 3) з (8n ² + 5n − 3).

Відповідь

4н ² + 12н

Вправа\(\PageIndex{16}\):

Відніміть: (a ² − 4a − 9) з (6a ² + 4a − 1).

Відповідь

5а ² + 8а + 8

Оцінити многочлен для заданого значення

У Мові алгебри ми оцінювали вирази. Оскільки поліноми є вирази, ми будемо слідувати тим же процедурам, щоб оцінити поліноми - підставити задане значення змінної в многочлен, а потім спростити.

Приклад\(\PageIndex{9}\):

Оцініть 3x 2 − 9x + 7, коли (a) x = 3 (b) x = −1

Рішення

(а) х = 3

Замініть 3 на x.	3 (3) ^2 − 9 (3) + 7
Спростити вираз з показником.	3 • 9 − 9 (3) + 7
Помножити.	27 − 27+ 7
Спростити.	7

(б) х = −1

Замініть -1 на x.	3 (-1) ^2 − 9 (-1) + 7
Спростити вираз з показником.	3 • 1 − 9 (-1) + 7
Помножити.	3 + 9 + 7
Спростити.	19

Вправа\(\PageIndex{17}\):

Оцінити: 2x ² + 4x − 3, коли (a) x = 2 (b) x = −3

Відповідь на

13

Відповідь б

3

Вправа\(\PageIndex{18}\):

Оцінити: 7y ² − y − 2, коли (a) y = −4 (b) y = 0

Відповідь на

114

Відповідь б

-2

Приклад\(\PageIndex{10}\):

Многочлен −16t 2 + 300 дає висоту об'єкта t секунд після його скидання з моста заввишки 300 футів. Знайти висоту після t = 3 секунди.

Рішення

Замініть 3 на t.	-16 (^32) +300
Спростити вираз з показником.	-16 • 9 + 300
Помножити.	-144 + 300
Спростити.	156

Вправа\(\PageIndex{19}\):

Многочлен −8t ² + 24t + 4 дає висоту м'яча t секунд після того, як він викидається в повітря, з початкової висоти 4 фути. Знайти висоту після t = 3 секунди.

Відповідь

4 фути

Вправа\(\PageIndex{20}\):

Многочлен −8t ² + 24t + 4 дає висоту м'яча x секунд після того, як він викидається в повітря, з початкової висоти 4 фути. Знайти висоту після t = 2 секунди.

Відповідь

20 футів

ДОСТУП ДО ДОДАТКОВИХ ОНЛАЙН-РЕСУРСІВ

Додавання многочленів

Віднімання многочленів

Практика робить досконалим

Визначте многочлени, мономи, біноми та триноми

У наступних вправах визначте, чи є кожен з многочленів мономіальним, біноміальним, триноміальним або іншим поліномом.

1. 5х + 2
2. з ² − 5z − 6
3. а ² + 9а + 18
4. −12р ⁴
5. на ³ − 8 років ² + 2р − 16
6. 10 − 9х
7. 23 р. ²
8. м ⁴ + 4м ³ + 6м ² + 4м + 1

Визначаємо ступінь многочленів

У наступних вправах визначте ступінь кожного многочлена.

9. 8а ⁵ − 2а ³ + 1
10. 5c ³ + 11c ² − c − 8
11. 3x − 12
12. 4 роки + 17
13. −13
14. −22

Додавання та віднімання мономи

У наступних вправах додайте або відніміть мономи.

15. 6х ² + 9х ²
16. 4 р ³ + 6 років ³
17. −12у + 4у
18. −3м + 9м
19. 5а + 7б
20. 8 років +6
21. Додати: 4а, − 3б, − 8а
22. Додайте: 4х, 3г, − 3х
23. 18x − 2х
24. 13а − 3а
25. Відніміть 5x ⁶ з − 12x ⁶
26. Відняти 2p ⁴ з − 7p ⁴

Додавання та віднімання многочленів

У наступних вправах додайте або відніміть поліноми.

27. (4 роки ² + 10 років + 3) + (8 років ² − 6 років + 5)
28. (7х ² − 9х + 2) + (6х ² − 4х + 3)
29. (х ² + 6х+ 8) + (−4х ² + 11х − 9)
30. (у ² + 9й + 4) + (−2й ² − 5й − 1)
31. (3а ² + 7) + (а ² − 7а − 18)
32. (p ² − 5п − 11) + (3п ² + 9)
33. (6м ² − 9м − 3) − (2м ² + м − 5)
34. (3n ² − 4n + 1) − (4n ² − n − 2)
35. (z ² + 8z + 9) − (z ² − 3z + 1)
36. (z ² − 7z + 5) − (z ² − 8z + 6)
37. (12 с ² − 15 с) − (с − 9)
38. (10р ² − 20р) − (r − 8)
39. Знайти суму (2p ³ − 8) і (p ² + 9p + 18)
40. Знайти суму (q ² + 4q + 13) і (7q ³ − 3)
41. Відняти (7x ² − 4x + 2) від (8x ² − х + 6)
42. Відняти (5x ² − x + 12) від (9x ² − 6x − 20)
43. Знайти різницю (w ² + w − 42) і (w ² − 10w + 24)
44. Знайти різницю (z ² − 3z − 18) і (z ² + 5z − 20)

Оцінити многочлен для заданого значення

У наступних вправах оцінюємо кожен многочлен за заданою величиною.

45. Оцініть 8 років ² − 3 роки + 2
    1. у = 5
    2. y = −2
    3. у = 0
46. Оцініть 5y ² − y − 7, коли:
    1. y = −4
    2. у = 1
    3. у = 0
47. Оцініть 4 − 36x, коли:
    1. х = 3
    2. х = 0
    3. x = −1
48. Оцініть 16 − 36x ², коли:
    1. x = −1
    2. х = 0
    3. х = 2
49. Омивач вікон скидає ракель з платформи висотою 275 футів. Многочлен −16t ² + 275 дає висоту ракеля t секунд після його скидання. Знайти висоту після t = 4 секунди.
50. Виробник мікрохвильових печей виявив, що дохід, отриманий від продажу мікрохвильових печей за ціною р доларів кожна, дається поліномом −5p ² + 350p. Знайти отриманий дохід, коли р = 50 доларів.

Щоденна математика

51. Економічність палива Економічність палива (в милі на галон) автобуса, що йде зі швидкістю х миль на годину, задається поліномом\(− \dfrac{1}{160} x^{2} + \dfrac{1}{2} x\). Знайдіть економічність палива, коли x = 40 миль/год.
52. Зупинний шлях Кількість футів, необхідних для автомобіля, який подорожує зі швидкістю x миль на годину, щоб зупинитися на сухому, рівному бетоні задається поліномом 0.06x ² + 1.1x. Знайдіть гальмівний шлях, коли x = 60 миль/год.

Письмові вправи

53. Використовуючи власні слова, поясніть різницю між моном, біноміальним і тріноміальним.
54. Елоїза вважає, що сума 5x ² + 3x ⁴ становить 8x ⁶. Що не так з її міркуваннями?

Самостійна перевірка

(а) Після виконання вправ використовуйте цей контрольний список, щоб оцінити своє володіння цілями цього розділу.

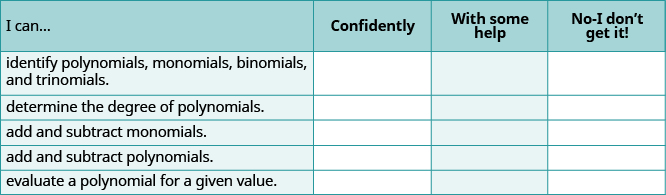
(b) Якщо більшість ваших перевірок були:

... впевнено. Вітаємо! Ви досягли цілей у цьому розділі. Подумайте про навички навчання, які ви використовували, щоб ви могли продовжувати їх використовувати. Що ви зробили, щоб стати впевненим у своїй здатності робити ці речі? Будьте конкретні.

... з деякою допомогою. Це потрібно вирішувати швидко, оскільки теми, які ви не освоюєте, стають вибоїнами на вашому шляху до успіху. У математиці кожна тема будується на попередній роботі. Важливо переконатися, що у вас міцний фундамент, перш ніж рухатися далі.

До кого можна звернутися за допомогою? Ваші колеги-однокласники та інструктор - хороші ресурси. Чи є в кампусі місце, де доступні репетитори з математики? Чи можна вдосконалити свої навички навчання?

... Ні—я цього не розумію! Це попереджувальний знак, і ви не повинні його ігнорувати. Ви повинні отримати допомогу відразу ж, інакше ви швидко будете перевантажені. Зверніться до інструктора, як тільки зможете обговорити вашу ситуацію. Разом ви можете придумати план, щоб отримати вам необхідну допомогу.

Автори та атрибуція

• Template:ContribOpenStaxPreAlgebra