10.S: Поліноми (резюме)

Ключові умови

біноміальних	Многочлен з рівно двома долями
ступінь константи	Ступінь константи дорівнює 0.
ступінь многочлена	Ступінь многочлена - найвища ступінь з усіх його членів.
ступінь строку	Ступінь члена многочлена є показником його змінної.
найбільший загальний фактор	Найбільшим загальним фактором (GCF) двох і більше виразів є найбільший вираз, який є фактором всіх виразів.
мономіальний	Член виду ax ^m, де a - константа, а m - ціле число, називається мономіалом.
негативний показник	Якщо n - натуральне число і a ≠ 0, то\(a^{-n} = \dfrac{1}{a^{n}}\).
многочлен	Многочлен - це моном, або два або більше мономи, об'єднані додаванням або відніманням.
наукові позначення	Число, виражене в науковому позначенні, коли воно має вигляд a × 10 ^n, де a ≥ 1 і a < 10, а n - ціле число.
тріпомінал	Триноміал - це многочлен з рівно трьома долями.
нульовий показник	Якщо a є ненульовим числом, то ^0 = 1. Будь-яке ненульове число, підняте до нульової потужності, дорівнює 1.

Ключові концепції

10.2 - Використовувати властивості множення показників

• Експоненціальне позначення

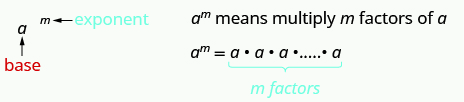
Це читається як до м ^го потужності.

• Властивість продукту експонентів
  • Якщо a - дійсне число, а m, n - підрахунок чисел, то a ^m • a ⁿ = a ^{m + n}
  • Щоб помножити з подібними основами, додайте показники.
• Власність потужності для експонентів
  • Якщо a - дійсне число, а m, n - підрахунок чисел, то (a ^m) ⁿ = a ^{m • n}
• Продукт до властивості влади для експонентів
  • Якщо a і b є дійсними числами, а m - цілим числом, то (ab) ^m = a ^m b ^m

10.3 - Множення многочленів

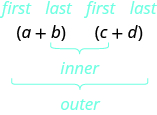
• Використовуйте метод FOIL для множення двох біноміалів.

Крок 1. Помножте Перші члени.
Крок 2. Помножте Зовнішні члени.
Крок 3. Помножте Внутрішні члени.
Крок 4. Помножте Останні члени.
Крок 5. Поєднуйте подібні терміни, коли це можливо.

• Множення двох біноміалів: Щоб помножити біноміали, використовуйте:
  • Розподільна власність
  • Фольга метод
  • вертикальний метод
• Множення триноміала на біноміал: Щоб помножити триноміал на біноміал, використовуйте:
  • Розподільна власність
  • вертикальний метод

10.4 - Розділити мономи

• Властивість еквівалентних дробів
  • Якщо a, b, c є цілими числами, де b ≠ 0, c ≠ 0, то $$\ dfrac {a} {b} =\ dfrac {a\ cdot c} {b\ cdot c}\ quad\ dfrac {a\ cdot c} {b\ cdot c} =\ dfrac {a} {b} $$
• Нульовий показник
  • Якщо a є ненульовим числом, то ⁰ = 1.
  • Будь-яке ненульове число, підняте до нульової потужності, дорівнює 1.
• Коефіцієнтна властивість для експонентів
  • Якщо a є дійсним числом, a ≠ 0, а m, n - цілі числа, то $$\ dfrac {a^ {m}} {a^ {n} = a^ {м-n},\; m>n\ quad\ dfrac {a^ {m}} {a^ {n}} =\ dfrac {1} {a^ {n-m},\; н>м$$
• Коефіцієнт до властивості влади для експонентів
  • Якщо a та b є дійсними числами, b ≠ 0, а m - лічильне число, то $$\ left (\ dfrac {a} {b}\ праворуч) ^ {m} =\ dfrac {a^ {m}} {b^ {m}} $$
  • Щоб підняти дріб до степеня, підніміть чисельник і знаменник до цієї міри.

10.5 - Цілочисельні показники та наукові позначення

• Резюме властивостей експоненти
  • Якщо a, b - дійсні числа, а m, n - цілі числа, то

Властивість продукту	а ^м • а ^н = а ^м + н
Власне майно	(А ^м) ^n = а ^м • н
Продукт у власність влади	(аб) ^м = а ^м б ^м
Частка власності	\(\dfrac{a^{m}}{a^{n}}\)= a ^m − n, a ≠ 0, м > n
	\(\dfrac{a^{m}}{a^{n}} = \dfrac{1}{a^{n-m}}\), a ≠ 0, n > м
Нульова властивість експоненти	a ^0 = 1, a ≠ 0
Коефіцієнт до власності влади	\(\left(\dfrac{a}{b}\right)^{m} = \dfrac{a^{m}}{b^{m}}\), b ≠ 0
Визначення негативного показника	\(a^{-n} = \dfrac{1}{a^{n}}\)

• Перетворити з десяткового позначення на наукове позначення: Щоб перетворити десяткове число в наукові позначення:
  1. Перемістіть десяткову крапку так, щоб перший множник був більшим або дорівнював 1, але менше 10.
  2. Підрахуйте кількість десяткових знаків, n, щоб десяткова крапка була переміщена. Напишіть число у вигляді добутку зі степенем 10.
     • Якщо вихідне число більше 1, то потужність 10 складе 10 ⁿ.
     • Якщо початкове число знаходиться в межах від 0 до 1, потужність 10 буде дорівнює 10 ⁿ.
  3. Перевірте.
• Перетворення наукового позначення в десяткову форму: Щоб перетворити наукові позначення в десяткову форму:
  1. Визначте показник, n, на коефіцієнт 10.
  2. Перемістіть десяткові n знаків, при необхідності додаючи нулі.
     • Якщо показник позитивний, пересуньте десяткову крапку на n розрядів вправо.
     • Якщо показник від'ємний, перемістіть десяткову крапку |n| місця вліво.
  3. Перевірте.

10.6 - Вступ до факторингових поліномів

• Знайдіть найбільший загальний фактор.
  1. Розподіліть кожен коефіцієнт на прості числа. Запишіть всі змінні з показниками в розгорнутому вигляді.
  2. Перелічити всі фактори, що відповідають загальним факторам у стовпці. У кожному стовпці обведіть загальні фактори.
  3. Збийте загальні фактори, які поділяють всі вирази.
  4. Помножте коефіцієнти.
• Розподільна власність
  • Якщо a, b, c - дійсні числа, то a (b + c) = ab + ac і ab + ac = a (b + c).
• Фактор найбільший загальний фактор з полінома.
  1. Знайдіть ЗКФ всіх членів многочлена.
  2. Перепишіть кожен термін як продукт за допомогою GCF.
  3. Використовуйте розподільну властивість «у зворотному напрямку» для фактора виразу.
  4. Перевірте, множивши коефіцієнти.

Дописувачі та атрибуція

• Template:ContribOpenStaxPreAlgebra