10.4: Множення многочленів (частина 1)

Last updated
Save as PDF

Page ID: 57882

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Помножити многочлен на мономіал
Помножити біноміал на біноміал
Помножте триноміал на біноміал

будьте готові!

Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

Розподілити: 2 (х + 3). Якщо ви пропустили проблему, перегляньте приклад 7.4.1.
Розподілити: −11 (4 − 3a). Якщо ви пропустили проблему, перегляньте приклад 7.4.10.
Поєднуйте як терміни: х ² + 9х+7х+63. Якщо ви пропустили проблему, перегляньте приклад 2.3.9.

Помножити многочлен на мономіал

У Distributive Property ви навчилися використовувати розподільну властивість для спрощення виразів, таких як 2 (x − 3). Ви помножили обидва члени в дужках, x і 3, на 2, щоб отримати 2x − 6. З новим словником цієї глави ви можете сказати, що ви множили біном, x − 3, на мономіал, 2. Множення біноміала на мономіал для вас не є новим!

Приклад$\PageIndex{1}$:

Множимо: 3 (x + 7).

Рішення

Розподілити.	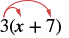$CNX_BMath_Figure_10_03_001_img-01.png$
	3 • х + 3 • 7
Спростити.	3х + 21

Вправа$\PageIndex{1}$:

Множимо: 6 (x + 8).

Відповідь: 6х + 48

Вправа$\PageIndex{2}$:

Множимо: 2 (у + 12).

Відповідь: 2 роки + 24

Приклад$\PageIndex{2}$:

Множення: x (x − 8).

Рішення

Розподілити.	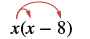$CNX_BMath_Figure_10_03_044_img-01.png$
	х ² - 8х
Спростити.	х ² - 8х

Вправа$\PageIndex{3}$:

Помножити: y (y − 9).

Відповідь: $ y^{2}-9 y$

Вправа$\PageIndex{4}$:

Множимо: p (p − 13).

Відповідь: $ p^2 - 13p$

Приклад$\PageIndex{3}$:

Множення: 10x (4x + y).

Рішення

Розподілити.	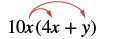$CNX_BMath_Figure_10_03_045_img-02.png$
	10х • 4х + 10х • у
Спростити.	40х ² + 10хх

Вправа$\PageIndex{5}$:

Множення: 8x (x + 3y).

Відповідь: $8x^2+24xy $

Вправа$\PageIndex{6}$:

Множимо: 3r (6r + с).

Відповідь: $18r^2+3rs $

Множення мономіала на тріноміал працює приблизно так само.

Приклад$\PageIndex{4}$:

Множення: −2x (5x ² + 7x − 3).

Рішення

Розподілити.	$CNX_BMath_Figure_10_03_046_img-01.png$
	-2х • 5х ² + (-2х) • 7х - (-2х) • 3
Спростити.	-10х ³ -14х ² + 6х

Вправа$\PageIndex{7}$:

Множення: −4y (8y ² + 5y − 9).

Відповідь: $-32y^3-20y^2+36y $

Вправа$\PageIndex{8}$:

Множення: −6x (9x ² + x − 1).

Відповідь: $ -54x^3-6x^2+6x$

Приклад$\PageIndex{5}$:

Множимо: 4y ³ (y ² − 8y + 1).

Рішення

Розподілити.	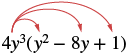$CNX_BMath_Figure_10_03_047_img-01.png$
	4 у ³ • у ² - 4й ³ • 8й + 4й ³ • 1
Спростити.	4й ⁵ -32й ⁴ + 4й ³

Вправа$\PageIndex{9}$:

Помножте: 3x ² (4x ² − 3x + 9).

Відповідь: $ 12 x^{4}-9 x^{3}+27 x^{2}$

Вправа$\PageIndex{10}$:

Множимо: 8y ² (3y ² − 2y − 4).

Відповідь: $24 y^{4}-16 y^{3}-32 y^{2} $

Тепер у нас буде мономіал як другий фактор.

Приклад$\PageIndex{6}$:

Множимо: (х + 3) р.

Рішення

Розподілити.	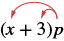$CNX_BMath_Figure_10_03_048_img-01.png$
	х • р + 3 • п
Спростити.	хр + 3р

Вправа$\PageIndex{11}$:

Множимо: (х + 8) р.

Відповідь: $xp+8p $

Вправа$\PageIndex{12}$:

Множимо: (a + 4) р.

Відповідь: $ap + 4p $

Помножте біноміал на біноміал

Подібно до того, як існують різні способи представлення множення чисел, існує кілька методів, які можуть бути використані для множення біноміального на біноміальне число.

Використання розподільної власності

Ми почнемо з використання розподільної властивості. Подивіться ще раз на приклад$\PageIndex{6}$.

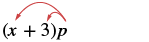	$CNX_BMath_Figure_10_03_049_img-01.png$
Ми розподілили р, щоб отримати	$CNX_BMath_Figure_10_03_049_img-02.png$
Що робити, якщо ми маємо (x + 7) замість p? Подумайте про (х + 7) як про$\textcolor{red}{p}$ вищезазначене.	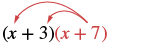$CNX_BMath_Figure_10_03_049_img-03.png$
Розподілити (х + 7).	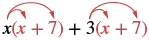$CNX_BMath_Figure_10_03_049_img-04.png$
Розподіліть ще раз.	х ² + 7х+3х+21
Поєднуйте подібні терміни.	х ² + 10х+21

Зверніть увагу, що перед об'єднанням подібних термінів у нас було чотири терміни. Ми помножили два члени першого біноміала на два члени другого двочлена - чотири множення.

Будьте обережні, щоб розрізняти суму від добутку.

\[\begin{split} &\textbf{Sum} \qquad \qquad \qquad \quad \textbf{Product} \\ &x + x \qquad \qquad \qquad \qquad x \cdot x \\ &\; \; 2x \qquad \qquad \qquad \qquad \qquad x^{2} \\ combine\; &like\; terms \qquad add\; exponents\; of\; like\; bases \end{split}\]

Приклад$\PageIndex{7}$:

Множимо: (x + 6) (x + 8).

Рішення

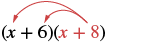	$CNX_BMath_Figure_10_03_050_img-01.png$
Розподілити (х + 8).	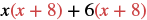$CNX_BMath_Figure_10_03_050_img-02.png$
Розподіліть ще раз.	х ² + 8х+6х+48
Спростити.	х ² + 14х+48

Вправа$\PageIndex{13}$:

Множимо: (x + 8) (x + 9).

Відповідь: $x^{2}+17 x+72 $

Вправа$\PageIndex{14}$:

Множимо: (a + 4) (a + 5).

Відповідь: $a^{2}+9 a+20 $

Тепер ми подивимося, як множити біноміали, де змінна має коефіцієнт.

Приклад$\PageIndex{8}$:

Множимо: (2x + 9) (3x + 4).

Рішення

Розподілити (3х+ 4).	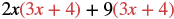$CNX_BMath_Figure_10_03_051_img-01.png$
Розподіліть ще раз.	6х ² + 8х +27х + 36
Спростити.	6х ² + 35х+36

Вправа$\PageIndex{15}$:

Множимо: (5х+ 9) (4х + 3).

Відповідь: $20 x^{2}+51 x+27 $

Вправа$\PageIndex{16}$:

Множимо: (10м + 9) (8м + 7).

Відповідь: $80 m^{2}+142 m+63 $

У попередніх прикладах біноміалами були суми. Коли є відмінності, ми приділяємо особливу увагу, щоб переконатися, що ознаки продукту правильні.

Приклад$\PageIndex{9}$:

Помножте: (4y + 3) (6y − 5).

Рішення

Розподілити.	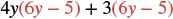$CNX_BMath_Figure_10_03_052_img-01.png$
Розподіліть ще раз.	24 роки − ² роки + 18 років − 15 років
Спростити.	24 роки − ² роки − 15

Вправа$\PageIndex{17}$:

Помножте: (7y+ 1) (8y − 3).

Відповідь: $ 56 y^{2}-13 y-3$

Вправа$\PageIndex{18}$:

Помножте: (3x + 2) (5x − 8).

Відповідь: $15 x^{2}-14 x-16 $

До цього моменту добуток двох біноміалів був тріноміальним. Це не завжди так.

Приклад$\PageIndex{10}$:

Помножити: (x + 2) (x − y).

Рішення

Розподілити.	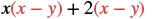$CNX_BMath_Figure_10_03_053_img-02.png$
Розподіліть ще раз.	х ² - х + 2х - 2г
Спростити.	Немає подібних термінів для комбінування.

Вправа$\PageIndex{19}$:

Помножити: (x + 5) (x − y).

Відповідь: $ x^{2}-x y+5 x-5 y$

Вправа$\PageIndex{20}$:

Помножте: (x + 2y) (x − 1).

Відповідь: $ x^{2}-x+2 x y-2 y$

Автори та атрибуція

Template:ContribOpenStaxPreAlgebra

Приклад\(\PageIndex{1}\):

Вправа\(\PageIndex{1}\):

Вправа\(\PageIndex{2}\):

Приклад\(\PageIndex{2}\):

Вправа\(\PageIndex{3}\):

Вправа\(\PageIndex{4}\):

Приклад\(\PageIndex{3}\):

Вправа\(\PageIndex{5}\):

Вправа\(\PageIndex{6}\):

Приклад\(\PageIndex{4}\):

Вправа\(\PageIndex{7}\):

Вправа\(\PageIndex{8}\):

Приклад\(\PageIndex{5}\):

Вправа\(\PageIndex{9}\):

Вправа\(\PageIndex{10}\):

Приклад\(\PageIndex{6}\):

Вправа\(\PageIndex{11}\):

Вправа\(\PageIndex{12}\):

Приклад\(\PageIndex{7}\):

Вправа\(\PageIndex{13}\):

Вправа\(\PageIndex{14}\):

Приклад\(\PageIndex{8}\):

Вправа\(\PageIndex{15}\):

Вправа\(\PageIndex{16}\):

Приклад\(\PageIndex{9}\):

Вправа\(\PageIndex{17}\):

Вправа\(\PageIndex{18}\):

Приклад\(\PageIndex{10}\):

Вправа\(\PageIndex{19}\):

Вправа\(\PageIndex{20}\):