5.5: Десяткові та дроби (частина 1)
- Page ID
- 57930
- Перетворення дробів на десяткові
- Порядок десяткових знаків і дробів
- Спрощення виразів за допомогою порядку операцій
- Знайти окружність і площу кіл
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Розділити: 0,24 ÷ 8. Якщо ви пропустили цю проблему, перегляньте приклад 5.4.9.
- Замовлення 0.64__0.6 за допомогою < or >. Якщо ви пропустили цю проблему, перегляньте приклад 5.2.7.
- Замовити −0.2__−0.1 за допомогою < or >. Якщо ви пропустили цю проблему, перегляньте приклад 5.2.8.
Перетворення дробів на десяткові
У Decimals ми навчилися перетворювати десяткові числа в дроби. Тепер ми зробимо зворотне - перетворить дробові дроби в десяткові. Пам'ятайте, що брусок дробу вказує на поділ. Так\(\dfrac{4}{5}\) може бути написано 4 ÷ 5 або\(5 \overline{)4}\). Це означає, що ми можемо перетворити дріб у десятковий, розглядаючи його як проблему ділення.
Щоб перетворити дріб в десятковий, розділіть чисельник дробу на знаменник дробу.
Запишіть дріб у\(\dfrac{3}{4}\) вигляді десяткового дробу.
Рішення
| Дробний бар означає ділення, тому ми можемо записати дріб 3 4, використовуючи ділення. | 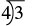 |
| Розділити. | 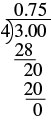 |
Так фракція\(\dfrac{3}{4}\) дорівнює 0,75.
Запишіть дріб у вигляді десяткового дробу:\(\dfrac{1}{4}\).
- Відповідь
-
\(0.25\)
Запишіть дріб у вигляді десяткового дробу:\(\dfrac{3}{8}\).
- Відповідь
-
\(0.375\)
Запишіть дріб у\(− \dfrac{7}{2}\) вигляді десяткового дробу.
Рішення
| Значення цього дробу від'ємне. Після ділення значення десяткового числа буде від'ємним. Робимо поділ ігноруючи знак, а потім записуємо негативний знак у відповідь. | $$-\ дфрак {7} {2} $$ |
| Розділіть 7 на 2. | 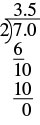 |
Отже,\(− \dfrac{7}{2}\) = −3.5.
Запишіть дріб у вигляді десяткового дробу:\(− \dfrac{9}{4}\).
- Відповідь
-
\(-2.25\)
Запишіть дріб у вигляді десяткового дробу:\(− \dfrac{11}{2}\).
- Відповідь
-
\(-5.5\)
Повторення десяткових знаків
Поки що у всіх прикладах перетворення дробів у десяткові числа ділення призвело до залишку нуля. Це не завжди так. Давайте подивимося, що відбувається, коли ми перетворюємо дріб\(\dfrac{4}{3}\) в десятковий. По-перше, зверніть увагу, що\(\dfrac{4}{3}\) це неправильний дріб. Його величина більше 1. Еквівалентне десяткове число також буде більше 1.
Ділимо 4 на 3.
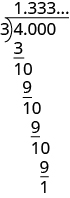
Незалежно від того, скільки ще нулів ми запишемо, завжди буде залишок 1, а трійки в частці будуть продовжуватися назавжди. Число 1.333... називається повторюваним десятковим. Пам'ятайте, що «...» означає, що візерунок повторюється.
Повторювана десяткова - це десяткова кома, в якій остання цифра або група цифр повторюється нескінченно.
Звідки ви знаєте, скільки «повторів» писати? Замість написання 1.333... ми використовуємо стенографічне позначення, розміщуючи рядок над цифрами, які повторюються. Повторюваний десятковий 1.333... записується 1. \(\overline{3}\). Рядок над 3 говорить вам, що 3 повторюється нескінченно. Отже, 1.333... = 1. \(\overline{3}\). Для інших десяткових знаків можуть повторюватися дві або більше цифр. \(\PageIndex{1}\)У таблиці наведено ще кілька прикладів повторюваних десяткових знаків.
| 1.333... = 1. \(\overline{3}\) | 3 - повторювана цифра |
| 4.1666... = 4.1\(\overline{6}\) | 6 - повторювана цифра |
| 4.161616... = 4. \(\overline{16}\) | 16 - повторюваний блок |
| 0.271271271... = 0. \(\overline{271}\) | 271 - повторюваний блок |
Запишіть\(\dfrac{43}{22}\) як десяткове число.
Рішення
Розділіть 43 на 22.
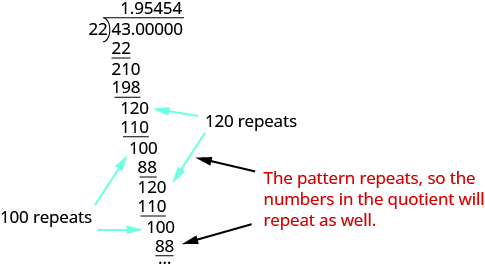
Зверніть увагу, що відмінності 120 і 100 повторюються, тому є повторення в цифрах частки; 54 буде повторюватися нескінченно. Перший десятковий знак у частці, 9, не є частиною візерунка. Отже,
\[\dfrac{43}{22} = 1.9 \overline{54}\]
Запишіть як десяткове число:\(\dfrac{27}{11}\).
- Відповідь
-
\(2. \overline{45}\)
Запишіть як десяткове число:\(\dfrac{51}{22}\).
- Відповідь
-
\(2.3 \overline{18}\)
Корисно конвертувати між дробами та десятковими числами, коли нам потрібно додати або відняти числа в різних формах. Щоб додати дріб і десятковий, наприклад, нам потрібно буде або перетворити дріб в десятковий або десятковий в дріб.
Спрощення:\(\dfrac{7}{8}\) + 6.4.
Рішення
| \(\dfrac{7}{8}\)Змінити на десяткову. |  |
0,875 + 6,4 |
| Додати. | 7.275 |
Спрощення:\(\dfrac{3}{8}\) + 4.9.
- Відповідь
-
\(5.275\)
Спрощення: 5.7 +\(\dfrac{13}{20}\).
- Відповідь
-
\(6.35\)
Порядок десяткових дробів і дробів
У десяткових знаках ми порівняли два десяткових знака і визначили, яка була більшою. Щоб порівняти десятковий дріб, ми спочатку перетворимо дріб у десятковий, а потім порівняємо десяткові числа.
Замовлення\(\dfrac{3}{8}\) __0.4 за допомогою < or >.
Рішення
| Перетворити\(\dfrac{3}{8}\) на десяткове число. | 0,375__0,4 |
| Порівняти 0.375 щоб 0.4 | 0,375 < 0,4 |
| Перепишіть з оригінальним дробом. | \(\dfrac{3}{8}\)< 0,4 |
Замовте кожну з наступних пар чисел, використовуючи < or >.
\[\dfrac{17}{20} \_ \_ \; 0.82\]
- Відповідь
-
\(>\)
Замовте кожну з наступних пар чисел, використовуючи < or >.
\[\dfrac{3}{4} \_ \_ \; 0.785\]
- Відповідь
-
\(<\)
При замовленні від'ємних чисел пам'ятайте, що більші числа знаходяться праворуч на числовому рядку, а будь-яке додатне число більше будь-якого від'ємного числа.
Замовлення −0.5___\(− \dfrac{3}{4}\) за допомогою < or >.
Рішення
| Перетворити\(− \dfrac{3}{4}\) на десяткове число. | −0,5___−0,75 |
| Порівняти −0,5 з −0,75. | −0.5 > −0,75 |
| Перепишіть нерівність з початковим дробом. | −0.5 >\(− \dfrac{3}{4}\) |
Замовте кожну з наступних пар чисел, використовуючи < or >:
\[− \dfrac{5}{8} \_ \_ −0.58\]
- Відповідь
-
\(<\)
Замовте кожну з наступних пар чисел, використовуючи < or >:
\[−0.53 \_ \_ − \dfrac{11}{20}\]
- Відповідь
-
\(>\)
Напишіть числа\(\dfrac{13}{20}\), 0,61,\(\dfrac{11}{16}\) в порядку від найменшого до найбільшого.
Рішення
| Перетворіть дроби в десяткові. | 0.65, 0.61, 0.6875 |
| Спочатку запишіть найменше десяткове число. | 0.61, ____, _____ |
| Запишіть наступне більше десяткове число в середньому місці. | 0.61, 0.65, _____ |
| Запишіть останнє десяткове число (більше) на третьому місці. | 0.61, 0.65, 0.6875 |
| Перепишіть список з оригінальними дробами. | 0,61,\(\dfrac{13}{20}, \dfrac{11}{16}\) |
Напишіть кожен набір чисел в порядку від найменшого до найбільшого:\(\dfrac{7}{8}, \dfrac{4}{5}\), 0.82.
- Відповідь
-
\(\frac{4}{5}\),\(0.82\),\(\frac{7}{8}\)
Напишіть кожен набір чисел в порядку від найменшого до найбільшого: 0,835,\(\dfrac{13}{16}, \dfrac{3}{4}\).
- Відповідь
-
\(\frac{3}{4}\),\(\frac{13}{16}\),\(0.835\)
Спрощення виразів за допомогою порядку операцій
Порядок операцій, введений в Use of Language of Algebra, також застосовується до десяткових знаків. Ви пам'ятаєте, що означає фраза «Будь ласка, вибачте мою дорогу тітку Саллі»?
Спрощення виразів: (a) 7 (18.3 − 21.7) (b)\(\dfrac{2}{3}\) (8.3 − 3.8)
Рішення
(а) 7 (18.3 − 21.7)
| Спрощення всередині дужок. | 7 (−3.4) |
| Помножити. | −23.8 |
(б)\(\dfrac{2}{3}\) (8.3 − 3.8)
| Спрощення всередині дужок. | $$\ дфрак {2} {3} (4.5) $$ |
| Запишіть 4.5 як дріб. | $$\ dfrac {2} {3}\ ліворуч (\ dfrac {4.5} {1}\ праворуч) $$ |
| Помножити. | $$\ фрак {9} {3} $$ |
| Спростити. | $3$$ |
Спрощення: (а) 8 (14.6 − 37,5) (b)\(\dfrac{3}{5}\) (9.6 − 2.1).
- Відповідь на
-
\(-183.2\)
- Відповідь б
-
\(4.5\)
Спрощення: (а) 25 (25.69 − 56,74) (b)\(\dfrac{2}{7}\) (11,9 − 4,2).
- Відповідь на
-
\(-776.25\)
- Відповідь б
-
\(2.2\)
Спрощення кожного виразу: (a) 6 ÷ 0,6 + (0,2) 4 − (0.1) 2 (b)\(\left(\dfrac{1}{10}\right)^{2}\) + (3.5) (0.9)
Рішення
(а) 6 ÷ 0,6 + (0,2) 4 − (0.1) 2
| Спрощення експонентів. | 6 ÷ 0,6 + (0,2) 4 − 0,01 |
| Розділити. | 10 + (0.2) 4 − 0,01 |
| Помножити. | 10 + 0,8 − 0,01 |
| Додати. | 10.8 − 0,01 |
| Відніміть. | 10.79 |
(б)\(\left(\dfrac{1}{10}\right)^{2}\) + (3,5) (0,9)
| Спрощення експонентів. | \(\dfrac{1}{100}\)+ (3.5) (0.9) |
| Помножити. | \(\dfrac{1}{100}\)+ 3.15 |
| Перетворити\(\dfrac{1}{100}\) на десяткове число. | 0,01 + 3,15 |
| Додати. | 3.16 |
Спрощення: 9 ÷ 0,9 + (0,4) 3 − (0,2) 2.
- Відповідь
-
\(11.16\)
Спрощення:\(\left(\dfrac{1}{2}\right)^{2}\) + (0.3) (4.2).
- Відповідь
-
\(1.51\)
