Skip to main content
LibreTexts - Ukrayinska

5.6: Десяткові та дроби (частина 2)

  1. Last updated
  2. Save as PDF
  • Page ID
    57939

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Знайдіть окружність і площу кіл

    Властивості кіл вивчалися вже понад 2000 років. Всі кола мають точно однакову форму, але на їх розміри впливає довжина радіуса, відрізка лінії від центру до будь-якої точки на колі. Відрізок лінії, який проходить через центр кола, що з'єднує дві точки на колі, називається діаметром. Діаметр в два рази більше радіуса. Див\(\PageIndex{1}\). Малюнок.

    Розмір кола можна виміряти двома способами. Відстань по колу називається його окружністю.

    Показаний коло. Пунктирна лінія, що проходить через найширшу частину кола, позначається як діаметр. Пунктирна лінія від центру кола до точки на колі позначається як радіус. По краю кола розташовується окружність.

    Малюнок\(\PageIndex{1}\)

    Архімед виявив, що для кіл всіх різних розмірів ділення окружності на діаметр завжди дає одне і те ж число. Значення цього числа - пі, що символізується грецькою літерою\(\pi\) (вимовляється пиріг). Однак точне значення\(\pi\) не може бути обчислене, оскільки десяткове число ніколи не закінчується і не повторюється (ми дізнаємося більше про такі числа в Властивості дійсних чисел.)

    Якщо ми хочемо точну окружність або площу кола, ми залишаємо символ\(\pi\) у відповіді. Ми можемо отримати приблизну відповідь, підставивши в якості значення 3.14\(\pi\). Ми використовуємо символ ≈, щоб показати, що результат приблизний, а не точний.

    Примітка: Властивості кіл

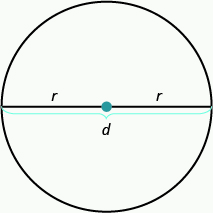
    Показаний коло. Через найширшу частину кола проходить лінія. У центрі кола є червона крапка. Половина лінії від центру кола до точки праворуч від кола позначена r Половина лінії від центру кола до точки зліва від кола також позначена r. Два ділянки, позначені r, мають дужку, намальовану внизу, що показує, що весь відрізок маркується d.

    r - довжина радіуса.

    d - довжина діаметра.

    Окружність - 2\(\pi\) р.\[C = 2 \pi r\]

    Площа -\(\pi\) r 2. \[A = \pi r^{2}\]

    Так як діаметр в два рази більше радіуса, ще один спосіб знайти окружність - скористатися формулою C =\(\pi\) d.

    Припустимо, ми хочемо знайти точну площу кола радіусом 10 дюймів. Щоб обчислити площу, ми б оцінили формулу для площі, коли r = 10 дюймів і залишили відповідь в терміні\(\pi\).

    \[\begin{split} A & = \pi r^{2} \\ A & = \pi (10^{2}) \\ A & = \pi \cdot 100 \end{split}\]

    Пишемо\(\pi\) після 100. Таким чином, точне значення площі дорівнює A = 100\(\pi\) квадратних дюймів. Щоб наблизити площу, ми б підставили\(\pi\) ≈ 3,14.

    \[\begin{split} A & = 100 \pi \\ & \approx 100 \cdot 3.14 \\ & \approx 314\; square\; inches \end{split}\]

    Не забудьте використовувати квадратні одиниці, такі як квадратні дюйми, коли ви обчислюєте площу.

    Приклад\(\PageIndex{10}\):

    Коло має радіус 10 сантиметрів. Приблизний його (а) окружність і (б) площа.

    Рішення

    (а) Знайдіть окружність, коли r = 10.

    Напишіть формулу для окружності. С = 2\(\pi\) р
    Замініть 3.14 для\(\pi\) і 10 на r. C ≈ 2 (3.14) (10)
    Помножити. C ≈ 62.8 сантиметра

    (б) Знайдіть площу, коли r = 10.

    Напишіть формулу для площі. А =\(\pi\) р 2
    Замініть 3.14 для\(\pi\) і 10 на r. A ≈ (3.14) (102)
    Помножити. A ≈ 314 квадратних сантиметрів
    Вправа\(\PageIndex{19}\):

    Коло має радіус 50 дюймів. Приблизний його (а) окружність і (б) площа.

    Відповідь

    314 в.

    Відповідь б

    7850 кв. дюймів

    Вправа\(\PageIndex{20}\):

    Коло має радіус 100 футів. Приблизний його (а) окружність і (б) площа.

    Відповідь

    628 футів

    Відповідь б

    31 400 кв. футів

    Приклад\(\PageIndex{11}\):

    Коло має радіус 42,5 сантиметра. Приблизний його (а) окружність і (б) площа.

    Рішення

    (а) Знайдіть окружність, коли r = 42,5.

    Напишіть формулу для окружності. С = 2\(\pi\) р
    Замініть 3.14 для\(\pi\) і 42.5 для r. C ≈ 2 (3.14) (42.5)
    Помножити. C ≈ 266.9 сантиметра

    (б) Знайдіть площу, коли r = 42,5.

    Напишіть формулу для площі. А =\(\pi\) р 2
    Замініть 3.14 для\(\pi\) і 42.5 для r. A ≈ (3.14) (42.5)
    Помножити. A ≈ 5671.625 квадратних сантиметрів
    Вправа\(\PageIndex{21}\):

    Коло має радіус 51,8 сантиметра. Приблизний його (а) окружність і (б) площа.

    Відповідь

    325.304 см

    Відповідь б

    8425.3736 кв. см

    Вправа\(\PageIndex{22}\):

    Коло має радіус 26,4 метра. Приблизний його (а) окружність і (б) площа.

    Відповідь

    165.792 км

    Відповідь б

    2188.4544 кв.м

    Орієнтовний\(\pi\) з дробу

    Перетворення дробу\(\dfrac{22}{7}\) в десятковий. Якщо ви використовуєте калькулятор, десяткове число заповнить дисплей і покаже 3.14285714. Але якщо ми округляємо це число до двох знаків після коми, ми отримаємо 3,14, десяткове наближення\(\pi\). Коли у нас є коло з радіусом, заданим у вигляді дробу, ми можемо замінити\(\dfrac{22}{7}\)\(\pi\) замість 3.14. І, оскільки\(\dfrac{22}{7}\) це також наближення π, ми будемо використовувати символ ≈, щоб показати, що ми маємо приблизне значення.

    Приклад\(\PageIndex{12}\):

    Коло має радіус\(\dfrac{14}{15}\) метра. Приблизний його (а) окружність і (б) площа.

    Рішення

    (а) Знайти окружність, коли r =\(\dfrac{14}{15}\)

    Напишіть формулу для окружності. С = 2\(\pi\) р
    \(\dfrac{22}{7}\)\(\pi\)Замінюємо і\(\dfrac{14}{15}\) на r. $C\ приблизно 2\ ліворуч (\ dfrac {22} {7}\ праворуч)\ ліворуч (\ dfrac {14} {15}\ праворуч) $$
    Помножити. C ≈\(\dfrac{88}{15}\) метрів

    . (б) Знайдіть площу, коли r =\(\dfrac{14}{15}\).

    Напишіть формулу для площі. А =\(\pi\) р 2
    \(\dfrac{22}{7}\)\(\pi\)Замінюємо і\(\dfrac{14}{15}\) на r. $A\ приблизно\ ліворуч (\ dfrac {22} {7}\ праворуч)\ ліворуч (\ dfrac {14} {15}\ праворуч) ^ {2} $$
    Помножити. A ≈\(\dfrac{616}{225}\) квадратних метрів
    Вправа\(\PageIndex{23}\):

    Коло має радіус\(\dfrac{5}{21}\) метрів. Приблизний його (а) окружність і (б) площа.

    Відповідь

    \(\frac{220}{147}\)м

    Відповідь б
    \(\frac{550}{3087}\)кв. м
    Вправа\(\PageIndex{24}\):

    Коло має радіус\(\dfrac{10}{33}\) дюймів. Приблизний його (а) окружність і (б) площа.

    Відповідь

    \(\frac{40}{21}\)в.

    Відповідь б
    \(\frac{200}{693}\)кв. в.
    ДОСТУП ДО ДОДАТКОВИХ ОНЛАЙН-РЕСУРСІВ

    Перетворення дробу в десятковий - Частина 2

    Перетворення дробу на десятковий (повторюваний)

    Порівняння дробів та десяткових дробів за допомогою символів нерівності

    Визначте площу кола

    Визначте окружність кола

    Практика робить досконалим

    Перетворення дробів на десяткові

    У наступних вправах перетворіть кожен дріб в десятковий.

    1. \(\dfrac{2}{5}\)
    2. \(\dfrac{4}{5}\)
    3. \(- \dfrac{3}{8}\)
    4. \(- \dfrac{5}{8}\)
    5. \(\dfrac{17}{20}\)
    6. \(\dfrac{13}{20}\)
    7. \(\dfrac{11}{4}\)
    8. \(\dfrac{17}{4}\)
    9. \(- \dfrac{310}{25}\)
    10. \(- \dfrac{284}{25}\)
    11. \(\dfrac{5}{9}\)
    12. \(\dfrac{2}{9}\)
    13. \(\dfrac{15}{11}\)
    14. \(\dfrac{18}{11}\)
    15. \(\dfrac{15}{111}\)
    16. \(\dfrac{25}{111}\)

    У наступних вправах спростіть вираз.

    1. \(\dfrac{1}{2}\)+ 6.5
    2. \(\dfrac{1}{4}\)+ 10,75
    3. 2.4 +\(\dfrac{5}{8}\)
    4. 3,9 +\(\dfrac{9}{20}\)
    5. 9.73 +\(\dfrac{17}{20}\)
    6. 6.29 +\(\dfrac{21}{40}\)

    Порядок десяткових дробів і дробів

    У наступних вправах замовляйте кожну пару чисел, використовуючи < or >.

    1. \(\dfrac{1}{8}\)___0.8
    2. \(\dfrac{1}{4}\)___0.4
    3. \(\dfrac{2}{5}\)___0.25
    4. \(\dfrac{3}{5}\)___0.35
    5. 0,725___\(\dfrac{3}{4}\)
    6. 0,92___\(\dfrac{7}{8}\)
    7. 0,66___\(\dfrac{2}{3}\)
    8. 0,83___\(\dfrac{5}{6}\)
    9. −0,75___\(- \dfrac{4}{5}\)
    10. −0,44___\(- \dfrac{9}{20}\)
    11. \(- \dfrac{3}{4}\)___−0.925
    12. \(- \dfrac{2}{3}\)___−0.632

    У наступних вправах запишіть кожен набір чисел в порядку від найменшого до найбільшого.

    1. \(\dfrac{3}{5}, \dfrac{9}{16}\), 0,55
    2. \(\dfrac{3}{8}, \dfrac{7}{20}\), 0,36
    3. 0,702,\(\dfrac{13}{20}, \dfrac{5}{8}\)
    4. 0,15,\(\dfrac{3}{16}, \dfrac{1}{5}\)
    5. −0,3,\(- \dfrac{1}{3}, - \dfrac{7}{20}\)
    6. −0,2,\(- \dfrac{3}{20}, - \dfrac{1}{6}\)
    7. \(- \dfrac{3}{4}, - \dfrac{7}{9}\), −0.7
    8. \(- \dfrac{8}{9}, - \dfrac{4}{5}\), −0.9

    Спрощення виразів за допомогою порядку операцій

    У наступних вправах спростити.

    1. 10 (25.1 − 43.8)
    2. 30 (18.1 − 32.5)
    3. 62 (9.75 − 4,99)
    4. 42 (8.45 − 5.97)
    5. \(\dfrac{3}{4}\)(12.4 − 4,2)
    6. \(\dfrac{4}{5}\)(8,6 + 3,9)
    7. \(\dfrac{5}{12}\)(30.58 + 17,9)
    8. \(\dfrac{9}{16}\)(21.96 − 9.8)
    9. 10 ÷ 0,1 + (1.8) 4 − (0.3) 2
    10. 5 ÷ 0,5 + (3,9) 6 − (0.7) 2
    11. (37,1 + 52,7) ÷ (12,5 ÷ 62,5)
    12. (11,4 + 16,2) ÷ (18 ÷ 60)
    13. \(\left(\dfrac{1}{5}\right)^{2}\)+ (1.4) (6.5)
    14. \(\left(\dfrac{1}{2}\right)^{2}\)+ (2.1) (8.3)
    15. \(− \dfrac{9}{10} \cdot \dfrac{8}{15}\)+ 0.25
    16. \(− \dfrac{3}{8} \cdot \dfrac{14}{15}\)+ 0.72

    Змішана практика

    У наступних вправах спростити. Дайте відповідь у вигляді десяткового дробу.

    1. \(3 \dfrac{1}{4}\)− 6,5
    2. \(5 \dfrac{2}{5}\)− 8,75
    3. 10,86 ÷\(\dfrac{2}{3}\)
    4. 5.79 ÷\(\dfrac{3}{4}\)
    5. \(\dfrac{7}{8}\)(103.48) +\(1 \dfrac{1}{2}\) (361)
    6. \(\dfrac{5}{16}\)(117,6) +\(2 \dfrac{1}{3}\) (699)
    7. 3.6\(\left(\dfrac{9}{8} − 2.72\right)\)
    8. 5.1\(\left(\dfrac{12}{5} − 3.91\right)\)

    Знайдіть окружність і площу кіл

    У наступних вправах орієнтуйте (а) окружність і (b) площа кожного кола. Якщо вимірювання наведені в дробах, залиште відповіді у вигляді дробів.

    1. радіус = 5 дюймів.
    2. радіус = 20 дюймів.
    3. радіус = 9 футів.
    4. радіус = 4 фути.
    5. радіус = 46 см
    6. радіус = 38 см
    7. радіус дії = 18,6 м
    8. радіус дії = 57.3 м
    9. радіус =\(\dfrac{7}{10}\) миля
    10. радіус =\(\dfrac{7}{11}\) миля
    11. радіус =\(\dfrac{3}{8}\) двір
    12. радіус =\(\dfrac{5}{12}\) двір
    13. діаметр =\(\dfrac{5}{6}\) м
    14. діаметр =\(\dfrac{3}{4}\) м

    Щоденна математика

    1. Келлі хоче придбати пару чобіт, які продаються\(\dfrac{2}{3}\) за оригінальною ціною. Початкова ціна чобіт - $84,99. Яка ціна продажу взуття?
    2. Архітектор планує поставити круглу мозаїку у вході в нову будівлю. Мозаїка буде у формі кола радіусом 6 футів. Скільки квадратних футів плитки знадобиться для мозаїки? (Округляйте відповідь до наступного цілого числа.)

    Письмові вправи

    1. Чи простіше вам перетворити десятковий в дріб або дріб в десятковий? Поясніть.
    2. Опишіть ситуацію у вашому житті, в якій вам може знадобитися знайти площу або окружність кола.

    Самостійна перевірка

    (а) Після виконання вправ використовуйте цей контрольний список, щоб оцінити своє володіння цілями цього розділу

    (б) Що цей контрольний список розповідає вам про ваше володіння цим розділом? Які кроки ви зробите для вдосконалення?

    Автори та авторства