5.2: Вступ до десяткових знаків

Last updated
Save as PDF

Page ID: 57285

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Нагадаємо, що цілі числа будуються за допомогою цифр.

Цифри

Набір

\[ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} \nonumber\nonumber \]

називається сукупністю цифр.

Як приклад, ціле число 55 555 («п'ятдесят п'ять тисяч п'ятсот п'ятдесят п'ять») будується за допомогою однієї цифри. Однак положення цифри 5 визначає її значення в числі 55 555. Перше виникнення

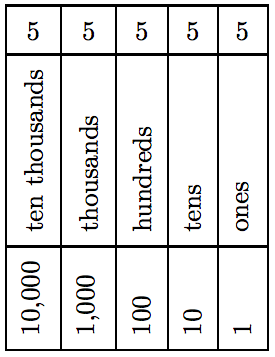
$Знімок екрана 2019-09-09 в 1.49.36 PM.png$

Таблиця 5.1: Значення місця.

цифра 5 буває в десятьтисячному місці, тому її значення становить 5 десять тисяч, або 50 000. Наступне входження цифри 5 знаходиться в тисячному місці, тому її значення становить 5 тисяч, або 5000. Дійсно, ціле число 55 555 в розгорнутому вигляді

50000 + 5000 + 500 + 50 + 5,

яка відображає значення цифри 5 в кожному місці.

Десяткове позначення

У таблиці 5.1 кожен раз, коли ви переміщуєте один стовпець ліворуч, значення місця в 10 разів перевищує значення місця попереднього стовпця. Навпаки, кожен раз, коли ви переміщуєте один стовпець праворуч, значення місця становить 1/10 від значення місця попереднього стовпця.

Тепер розглянемо десяткове число 12.3456, яке складається з трьох частин: цілої числової частини, десяткової крапки і дробової частини.

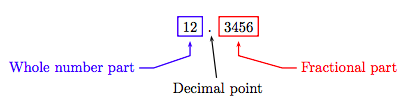
$Знімок екрана 2019-09-09 в 1.50.55 PM.png$

Ціла числова частина десяткового числа - це та частина, яка лежить строго лівіше десяткової крапки, а місце кожної цифри в цілій числовій частині задається стовпцями, показаними в таблиці 5.1.

Дробова частина десяткового числа - це та частина, яка лежить строго праворуч від десяткової крапки. Як ми бачили в таблиці 5.1, кожен стовпець має значення, рівне 1/10 від значення стовпця, який лежить безпосередньо ліворуч. Таким чином, не дивно, що:

Перший стовпець праворуч від десяткової крапки має місце значення 1/10 (десятих).
Другий стовпець праворуч від десяткової крапки має місце значення 1/100 (соті).
Третій стовпець праворуч від десяткової крапки має місце значення 1/1000 (тисячні частки).
Четвертий стовпець праворуч від десяткової крапки має місце значення 1/10000 (десятитисячних).

Ці результати зведені для десяткового числа 12.3456 в таблиці 5.2.

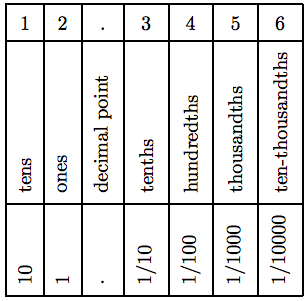
$Знімок екрана 2019-09-09 в 1.51.59 PM.png$

Таблиця 5.2: Значення місця.

Вимовлення десяткових чисел

Десяткове число 12.3456 складається з 1 десяти, 2 одиниць, 3 десятих, 4 сотих, 5 тисячних і 6 десятитисячних (див. Таблицю 5.2), і може бути записано в розгорнутому вигляді як

\[12.3456 = 10 + 2 + \frac{3}{10} + \frac{4}{100} + \frac{5}{1000} + \frac{6}{10000}.\nonumber \]

Зверніть увагу, що цілі числа можна об'єднати, а дроби записувати спільним знаменником і підсумувати.

\[ \begin{aligned} 12.3456 & = 12 + \frac{3 \cdot \textcolor{red}{1000}}{10 \cdot \textcolor{red}{1000}} + \frac{4 \cdot \textcolor{red}{100}}{100 \cdot \textcolor{red}{100}} + \frac{5 \cdot \textcolor{red}{10}}{1000 \cdot \textcolor{10}} + \frac{6}{10000} \\ & = 12 + \frac{3000}{10000} + \frac{400}{10000} + \frac{50}{10000} + \frac{6}{10000} \\ & = 12 + \frac{3456}{10000} \end{aligned}\nonumber \]

Результат підказує нам, як вимовляється число 12.3456. Вимовляється «дванадцять і три тисячі, чотириста пятьдесят шість десятитисячних».

Приклад 1

Розставте десяткове число 1,234,56 в розгорнутому вигляді, потім об'єднайте цілу цифрову частину і підсумуйте дробову частину над загальним знаменником. Використовуйте результат, щоб допомогти вимовити десяткове число.

Рішення

У розгорнутому вигляді,

\[1, 234.56 = 1, 000 + 200 + 30 + 4 + \frac{5}{10} + \frac{6}{100}\nonumber \]

Підсумуйте ціле число частин. Висловіть дробові частини як еквівалентні дроби і об'єднайте над одним спільним знаменником.

\[ \begin{aligned} = 1,234 + \frac{5 \cdot \textcolor{10}}{10 \cdot \textcolor{red}{10}} + \frac{6}{100} \\ = 1,234 + \frac{50}{100} + \frac{6}{100} \\ = 1, 234 + \frac{56}{100} \end{aligned}\nonumber \]

Звідси, 1 234,56 вимовляється «тисяча, двісті тридцять чотири і п'ятдесят шість сотих».

Вправа

Розставте десяткове число 3,502.23 в розгорнутому вигляді, потім об'єднайте цілу цифрову частину і підсумуйте дробову частину над загальним знаменником.

Відповідь: $3,502 + \frac{23}{100}$

Приклад 2

Розставте десяткове число 56.128 в розгорнутому вигляді, потім об'єднайте цілу цифрову частину і підсумуйте дробову частину над загальним знаменником. Використовуйте результат, щоб допомогти вимовити десяткове число.

Рішення

У розгорнутому вигляді,

\[56.128 = 50 + 6 + \frac{1}{10} + \frac{2}{100} + \frac{8}{1000}\nonumber \]

\[ \begin{aligned} = 56 + \frac{1 \cdot \textcolor{red}{100}}{10 \cdot \textcolor{red}{100}} + \frac{2 \cdot \textcolor{red}{10}}{100 \cdot \textcolor{red}{10}} + \frac{8}{1000} \\ = 56 + \frac{100}{1000} + \frac{20}{1000} + \frac{8}{1000} \\ = 56 + \frac{128}{1000} \end{aligned}\nonumber \]

Так, 56.128 вимовляється «п'ятдесят шість і сто двадцять вісім тисячних».

Вправа

Розставте десяткове число 235.568 в розгорнутому вигляді, потім об'єднайте цілу цифрову частину і підсумуйте дробову частину над загальним знаменником.

Відповідь: $235 + \frac{568}{1000}$

Обговорення та приклад призводить до наступного результату.

Як читати десяткове число

Вимовте цілу цифрову частину зліва від десяткового числа, як і будь-яке ціле число.
Скажіть слово «і» для десяткової крапки.
Вкажіть дробову частину праворуч від десяткового числа, як і будь-яке ціле число, а потім місце значення цифри в крайньому правому стовпці.

Приклад 3

Вимовте десяткове число 34.12.

Рішення

Сама права цифра в дробовій частині 34.12 знаходиться в стовпі сотих. Таким чином, 34.12 вимовляється «тридцять чотири і дванадцять сотих».

Вправа

Вимовляється 28.73

Відповідь: «Двадцять вісім і сімдесят три соті»

Важливий момент

При вимові десяткових чисел десяткова крапка читається як «і». Жоден інший приклад слова «і» не повинен з'являтися у вимові.

Приклад 4

Поясніть, чому «чотириста тридцять чотири і дві десяті» - неправильне вимова десяткового числа 434.2.

Рішення

Десяткова крапка читається як «і». Ніяке інше входження слова «і» у вимові не допускається. Правильна вимова має бути «чотириста тридцять чотири і дві десяті».

Вправа

Вимовляється 286.9.

Відповідь: «Чотириста тридцять чотири і дві десяті»

Приклад 5

Вимовте десяткове число 5,678.123.

Рішення

Сама права цифра в дробовій частині 5 678.123 знаходиться в тисячному стовпці. Отже, 5 678.123 вимовляється «5 тисяч шістсот сімдесят вісім і сто двадцять три тисячні».

Вправа

Вимовляють 7, 002.207

Відповідь: Відповідь: «Сім тисяч двохсот сім тисячних».

приклад 6

Вимовте десяткове число 995.4325.

Рішення

Сама права цифра в дробовій частині 995,4325 знаходиться в десятитисячній колонці. Отже, 995.4325 вимовляється «дев'ятсот дев'яносто п'ять і чотири тисячі триста двадцять п'ять десятитисячних».

Вправа

Вимовляє 500.1205.

Відповідь: Відповідь: «П'ятсот одна тисяча двісті п'ять десятитисячних».

Десяткові дроби до дробів

Оскільки ми тепер маємо можливість вимовляти десяткові числа, це проста вправа змінити десяткове число на дріб. ¹ Наприклад, 134.12 вимовляється «сто тридцять чотири і дванадцять сотих», тому його легко можна записати як змішаний дріб.

\[134.12 = 134 \frac{12}{100}\nonumber \]

Але ця змішана фракція може бути змінена на невідповідну фракцію.

\[ \begin{aligned} 134 \frac{12}{100} \\ & = \frac{100 \cdot 134 + 12}{100} & = \frac{13400 + 12}{100} \\ * = \frac{13412}{100} \end{aligned}\nonumber \]

Зверніть увагу, що чисельник - це наше вихідне число без десяткової крапки. У вихідному числі два знака після коми, а знаменник кінцевого неправильного дробу містить два нулі.

Це обговорення призводить до наступного результату.

¹ Зміна дробів на десяткові знаки буде розглянуто в розділі 5.5.

Зміна десяткових дробів на неправильні дроби

Щоб змінити десяткове число на неправильний дріб, дійте наступним чином:

Створіть дріб.
Помістіть десяткове число в чисельнику без десяткової крапки.
Підрахуйте кількість десяткових знаків. Помістіть рівну кількість нулів в знаменнику.

приклад 7

Змініть такі десяткові числа на неправильні дроби: (a) 1.2345 та (b) 27.198.

Рішення

У кожному випадку помістіть число в чисельник без десяткової крапки. У знаменнику додайте кількість нулів, рівне кількості десяткових знаків.

а) Десяткове число 1.2345 має чотири знака після коми. Отже,

\[1.2345 = \frac{12345}{10000}\nonumber \]

б) Десяткове число 27.198 має три знака після коми. Отже,

\[27.198 = \frac{27198}{1000}\nonumber \]

Вправа

Змініть 17.205 на неправильний дріб.

Відповідь: $\frac{17205}{100}$

приклад 8

Змініть кожну з наступних десяткових дробів на дроби, зменшені до найнижчих чисел: (a) 0,35 та (b) 0,125.

Рішення

Помістіть кожне число в чисельнику без десяткової крапки. Помістіть в знаменник число нулів, рівне кількості десяткових знаків. Знизити до найнижчих термінів.

а) По-перше, місце 35 понад 100.

\[0.35 = \frac{35}{100}\nonumber \]

Ми можемо розділити і чисельник, і знаменник на найбільший спільний дільник.

\[ \begin{aligned} = \frac{35 \div 5}{100 \div 5} ~ & \textcolor{red}{ \text{ Divide numerator and denominator by 5.}} \\ = \frac{7}{20} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]

б) По-перше, місце 125 над 1000.

\[0.125 = \frac{125}{1000}\nonumber \]

Простий коефіцієнт і скасування загальних факторів.

\[ \begin{aligned} = \frac{5 \cdot 5 \cdot 5}{2 \cdot 2 \cdot 2 \cdot 5 \cdot 5 \cdot 5} ~ & \textcolor{red}{ \text{ Prime factor numerator and denominator.}} \\ = \frac{ \cancel{5} \cdot \cancel{5} \cdot \cancel{5}}{2 \cdot 2 \cdot 2 \cdot \cancel{5} \cdot \cancel{5} \cdot \cancel{5}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{1}{8} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Вправа

Змініть 0,375 на дріб, зведений до найнижчих показників.

Відповідь: 3/8

Округлення

Правила округлення десяткових чисел практично ідентичні правилам округлення цілих чисел. По-перше, трохи термінології.

Цифра округлення та контрольна цифра

Цифра в місці, до якого ми хочемо округлити, називається цифрою округлення, а цифра, яка слідує за її безпосереднім праворуч, називається контрольною цифрою.

Якщо ми хочемо округлити десяткове число 12.254 до найближчої сотої, то цифра округлення дорівнює 5, а тестова цифра - 4.

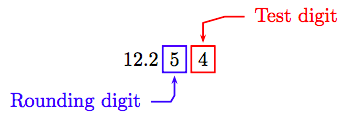
$Знімок екрана 2019-09-09 в 2.32.22 PM.png$

Якби ми використовували правила округлення цілих чисел, оскільки тестова цифра 4 менше 5, ми б замінили всі цифри праворуч від округлення нулями, щоб отримати наступне наближення.

12.254 ≈ 12.250

Однак, тому що

\[12.250 = 12 \frac{250}{1000} = 12 \frac{25}{100},\nonumber \]

кінцевий нуль в кінці дробової частини не має значення. Значить, ми обрізаємо кожну цифру після округлення цифри і використовуємо наступне наближення.

12.254 ≈ 12.25

Важливе спостереження

Видалення кінцевих нулів з кінця дробової частини десяткового числа не змінює його значення.

Вищенаведене обговорення мотивує наступний алгоритм округлення десяткових чисел.

Округлення десяткових чисел

Знайдіть цифру округлення і контрольну цифру.

Якщо контрольна цифра більше або дорівнює 5, додайте 1 до цифри округлення і обрізайте всі цифри праворуч від округлення цифри.
Якщо тестова цифра менше 5, просто обрізати всі цифри праворуч від округлення цифри.

приклад 9

Округлити 8,7463 до найближчої сотої.

Рішення

Знайдіть цифру округлення на сотих місцях і контрольну цифру праворуч від неї.

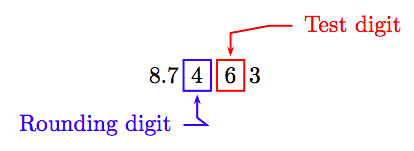
альт $Знімок екрана 2019-09-09 в 2.38.01 PM.png$

Оскільки тестова цифра більше 5, додайте 1 до цифри округлення і обрізайте всі цифри праворуч від округлення цифри. Значить, до найближчих сотих:

8.7463 ≈ 8.75

Вправа

Округлення 9.2768 до найближчої сотої.

Відповідь: 9.28

приклад 10

Округлення 113.246 до найближчого десятого.

Рішення

Знайдіть цифру округлення в десятому місці, а контрольну цифру - праворуч від неї.

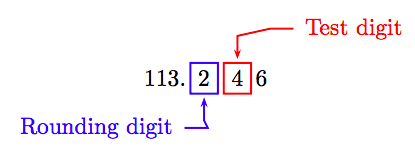
$Знімок екрана 2019-09-09 в 2.38.08 PM.png$

Оскільки тестова цифра менше 5, обрізати всі цифри праворуч від округлення цифри. Значить, до найближчої десятої:

113.246 ≈ 113.2

Вправа

Округлення 58.748 до найближчої десятої.

Відповідь: 58.7

Порівняння десяткових знаків

Ми можемо порівняти два додатних десяткових знаків, порівнюючи цифри в кожному місці, коли ми рухаємося зліва направо, місце за місцем. Наприклад, припустимо, ми хочемо порівняти десяткові числа 5.234 і 5.2357. По-перше, додайте достатню кількість кінцевих нулів до десяткового числа з меншою кількістю десяткових знаків, щоб числа мали однакову кількість десяткових знаків. При цьому зверніть увагу, що

\[ 5.234 = 5 \frac{234}{1000} = 5 \frac{2340}{10000} = 5.2340.\nonumber \]

Важливе спостереження

Додавання кінцевих нулів до кінця дробової частини десяткового числа не змінює його значення.

Далі вирівнюємо цифри наступним чином.

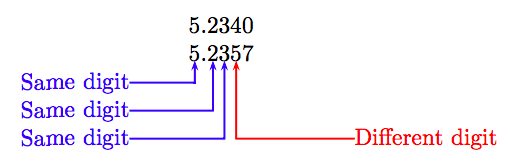
$Знімок екрана 2019-09-09 в 2.38.16 PM.png$

У міру сканування стовпців, рухаючись зліва направо, перше місце, яке має різні цифри, відбувається в тисячному місці, де цифра 5 - друге число більше цифри 4 в першому ж місці. Оскільки 5 більше 4, друге число більше першого. Тобто:

5.234 < 5,2357

Це обговорення передбачає наступний алгоритм.

Порівняння додатних десяткових чисел

Додайте достатню кількість кінцевих нулів, щоб обидва числа мали однакову кількість десяткових знаків.
Порівняйте цифри в кожному місці, рухаючись зліва направо.
Як тільки ви знайдете дві цифри в одному і тому ж місці, які відрізняються, десяткове число з найбільшою цифрою в цьому місці є більшим числом.

Приклад 11

Порівняйте 4.25 і 4.227.

Рішення

Додайте кінцевий нуль до першого десяткового числа і вирівняйте числа наступним чином.

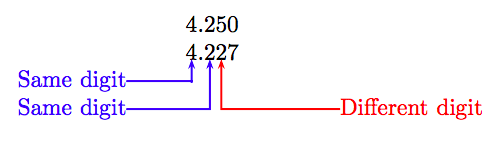
$Знімок екрана 2019-09-09 в 2.38.23 PM.png$

Перша відмінність полягає в сотих місцях, де цифра 5 в першому числі більше цифри 2 на тому ж місці другого числа. Отже, перше число більше другого; тобто:

4.25 > 4.227

Вправа

Порівняйте 8.34 і 8.348.

Відповідь: 8.34 < 8,348

При порівнянні від'ємних чисел число з більшою величиною є меншим числом. Отже, ми повинні налаштувати наш алгоритм порівняння від'ємних десяткових чисел.

Порівняння негативних десяткових чисел

Додайте достатню кількість кінцевих нулів, щоб обидва числа мали однакову кількість десяткових знаків.
Порівняйте цифри в кожному місці, рухаючись зліва направо.
Як тільки ви знайдете дві цифри в одному і тому ж місці, які відрізняються, десяткове число з найбільшою цифрою в цьому місці є меншим числом.

Приклад 12

Порівняйте −4.25 та −4.227.

Рішення

Додайте кінцевий нуль до першого десяткового числа і вирівняйте числа наступним чином.

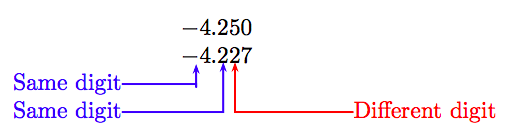
$Знімок екрана 2019-09-09 о 2.38.30 PM.png$

Перша відмінність полягає в сотих місцях, де цифра 5 в першому числі більше цифри 2 на тому ж місці другого числа. Отже, перше число менше другого; тобто:

−4,25 < −4,227

Вправа

Порівняйте −7.86 та −7.85.

Відповідь: −7,86 < −7,85

Вправи

1. Яка цифра знаходиться в десятому стовпці числа 4,552.0908?

2. Яка цифра знаходиться в тисячному стовпці числа 7,881.6127?

3. Яка цифра знаходиться в десятому стовпці числа 4,408.2148?

4. Яка цифра знаходиться в десятому стовпці числа 9,279.0075?

5. Яка цифра знаходиться в десятитисячному стовпці числа 2,709.5097?

6. Яка цифра знаходиться в стовпці сотих чисел 1,743.1634?

7. Яка цифра знаходиться в стовпі сотих числа 3,501.4456?

8. Яка цифра знаходиться в десятитисячному стовпці числа 9,214.3625?

9. Яка цифра знаходиться в стовпці сотих чисел 5,705.2193?

10. Яка цифра знаходиться в сотих стовпці числа 7,135.2755?

11. Яка цифра знаходиться в десятому стовпці числа 8,129.3075?

12. Яка цифра знаходиться в тисячному стовпці числа 6,971.4289?

У вправах 13-20 запишіть задане десяткове число в розгорнутому вигляді.

13. 46.139

14. 68,392

15. 643.19

16. 815,64

17. 14 829

18. 45,913

19. 658,71

20. 619,38

У вправах 21-28 дотримуйтесь процедури, наведеної в прикладах 1 і 2, щоб записати десяткове число в розгорнутому вигляді, потім об'єднати цілу цифрову частину і підсумувати дробову частину над загальним знаменником.

21. 32.187

22. 35,491

23. 36,754

24. 89.357

25. 596,71

26. 754,23

27. 527.49

28. 496,15

У вправах 29-40 вимовте задане десяткове число. Випишіть свою відповідь словами.

29. 0,9837

30. 0,6879

31. 0,2653

32. 0,8934

33. 925.47

34. 974,35

35. 83,427

36. 32.759

37. 63,729

38. 85.327

39. 826.57

40. 384,72

У вправах 41-52 перетворіть задану десяткову дробу в змішаний дріб. Чи не спрощуйте свою відповідь.

41. 98,1

42. 625.591

43. 781,7

44. 219.999

45. 915,239

46. 676.037

47. 560,453

48. 710,9

49. 414,939

50. 120,58

51. 446.73

52. 653,877

У вправах 53-60 перетворіть заданий десятковий дріб в неправильний дріб. Чи не спрощуйте свою відповідь.

53. 8,7

54. 3.1

55. 5,47

56. 5,27

57. 2.133

58. 2,893

59. 3,9

60. 1,271

У вправах 61-68 перетворіть задане десяткове число в дріб. Зменшіть свою відповідь до найнижчих термінів.

61. 0,35

62. 0,38

63. 0,06

64. 0,84

65. 0,98

66. 0,88

67. 0,72

68. 0,78

69. Округлення 79.369 до найближчої сотої.

70. Округлення 54.797 до найближчої сотої.

71. Раунд 71.2427 до найближчої тисячної.

72. Округлення 59,2125 до найближчої тисячної.

73. Раунд 29.379 до найближчого десятого.

74. Округлення 42,841 до найближчої десятої.

75. Округлення 89.3033 до найближчої тисячної.

76. Округлення 9.0052 до найближчої тисячної.

77. Округлення 20.655 до найближчої десятої.

78. Округлення 53,967 до найближчого десятого.

79. Округлення 19,854 до найближчої сотої.

80. Округлення 49,397 до найближчої сотої.

У вправах 81-92 визначте, яке з двох заданих тверджень вірно.

81. 0,30387617 < 0.3036562 or 0.30387617 > 0,3036562

82. 8,5934 < 8.554 or 8.5934 > 8,554

83. −0.034 < −0.040493 or −0.034 > −0.040493

84. −0.081284 < −0.08118 or −0.081284 > −0.08118

85. −8,3527 < −8.36553 or −8.3527 > −8,36553

86. −0,00786 < −0.0051385 or −0.00786 > −0,0051385

87. 18,62192 < 18.6293549 or 18.62192 > 18,6293549

88. 514.873553 < 514.86374 or 514.873553 > 514.86374

89. 36,8298 < 36.8266595 or 36.8298 > 36,8266595

90. 0,000681 < 0.00043174 or 0.000681 > 0,00043174

91. −15.188392 < −15.187157 or −15.188392 > −15.187157

92. −0.049785 < −0.012916 or −0.049785 > −0.012916

93. Запишіть десяткове число прописом.

i) Нещодавно виявлений 7.03-каратний синій діамант, виставлений на аукціоні в Sotheby's.

ii) Нещодавно запущений європейський телескоп Планка залишиться на орбіті 1,75 року вимірювання випромінювання Великого вибуху.

iii) Сонце складає 0,9985 маси в нашій Сонячній системі.

iv) Частинки глини дрібні - всього 0,0001 дюйма.

94. Швидкість світла. Індекс заломлення для даного матеріалу - це значення, яке представляє кількість разів повільніше світлової хвилі, що рухається в цьому конкретному матеріалі, ніж вона рухається у вакуумі простору.

i) Змініть порядок матеріалів за їх показником заломлення від найнижчого до найвищого.

ii) У скільки разів повільніше світлова хвиля в діаманті в порівнянні з вакуумом?

Матеріал	Індекс заломлення
Діамант	2.417
Вакуум	1.0000
оргскло	1.51
Повітря	1.0003
Вода	1.333
Циркон	1.923
Корона Скло	1.52
Лід	1.31

95. Коротший день? Вчені з лабораторії реактивного руху НАСА підрахували, що землетрус в Чилі, можливо, скоротив тривалість дня на Землі на 1,26 мільйонні частки секунди.

i) Запишіть це число повністю як десяткове число.

ii) Фактичні спостереження за тривалістю дня з точністю до п'яти мільйонних часток секунди. Запишіть цей дріб як десятковий.

iii) Порівняння двох десяткових знаків вище та визначте, який менший. Як ви думаєте, чи можуть вчені спостерігати і вимірювати розрахункове уповільнення землі?

Відповіді

1. 0

3. 2

5. 7

7. 4

9. 1

11. 3

13. $40 + 6 + 1 10 + \frac{3}{100} + \frac{9}{1000}$

15. $600 + 40 + 3 + \frac{1}{10} + \frac{9}{100}$

17. $10 + 4 + \frac{8}{10} + \frac{2}{100} + \frac{9}{1000}$

19. $600 + 50 + 8 + \frac{7}{10} + \frac{1}{100}$

21. $32 + \frac{187}{1000}$

23. $36 + \frac{754}{1000}$

25. $596 + \frac{71}{100}$

27. $527 + \frac{49}{100}$

29. дев'ять тисяч вісімсот тридцять сім десятитисячних

31. Дві тисячі шістсот пятьдесят три десятитисячні

33. дев'ятсот двадцять п'ять і сорок сім сотих

35. вісімдесят три і чотириста двадцять сім тисячних

37. шістдесят три і сімсот двадцять дев'ять тисячних

39. вісімсот двадцять шість і п'ятдесят сім сотих

41. $98 \frac{1}{10}$

43. $781 \frac{7}{10}$

45. $915 \frac{239}{1000}$

47. $560 \frac{453}{1000}$

49. $414 \frac{939}{1000}$

51. $446 \frac{73}{100}$

53. $\frac{87}{10}$

55. $\frac{547}{100}$

57. $\frac{2133}{1000}$

59. \ (\ гідророзрив {39} {10} |)

61. $\frac{7}{20}$

63. $\frac{3}{50}$

65. \ (\ гідророзрив {49} {50} |)

67. $\frac{18}{25}$

69. 79.37

71. 71.243

73. 29,4

75. 89.303

77. 20,7

79. 19,85

81. 0,30387617 > 0,3036562

83. −0,034 > −0.040493

85. −8,3527 > −8,36553

87. 18,62192 < 18,6293549

89. 36,8298 > 36,8266595

91. −15.188392 < −15.187157

93.

i) сім і три сотих

ii) одна і сімдесят п'ять сотих

iii) дев'ять тисяч дев'ятсот вісімдесят п'ять десятитисячних

iv) одна десятитисячна частина дюйма

95.

i) 0.00000126

ii) 0,000005

iii) 0.00000126 < 0.000005; вчені не змогли б виміряти розрахункову зміну тривалості дня.