7.2: Складні відсотки
- Page ID
- 66588
З простим інтересом ми припускали, що ми кишені відсотки, коли отримали його. На стандартному банківському рахунку будь-які відсотки, які ми отримуємо, автоматично додаються до нашого балансу, і ми отримуємо відсотки на ці відсотки в наступні роки. Таке реінвестування відсотків називається компаундуванням.
Припустимо, що ми вносимо $1,000 на банківський рахунок, що пропонує 3% відсотків, що складаються щомісяця. Як будуть рости наші гроші?
Відсотки 3% - це річна процентна ставка (APR) - загальна сума відсотків, що підлягають сплаті протягом року. Так як відсотки виплачуються щомісяця, кожен місяць ми будемо заробляти\(\dfrac{3 \%}{12} = 0.25 \%\) в місяць.
У перший місяць
\(P_0 = $1000\)
\(r = 0.0025 (0.25\%) \)
\(I = $1000 (0.0025) = $2.50\)
\(A = $1000 + $2.50 = $1,002.5\)
У перший місяць ми заробимо 2,50 долара відсотка, збільшивши залишок нашого рахунку до $1,002,50. У другому місяці
\(P_0 = $1,002.50\)
\(I = $1002.50 (0.0025) = $2.51\)(округлі)
\(A = $1002.50 + $2.51 = $1005.01\)
Зверніть увагу, що на другому місяці ми заробили більше відсотків, ніж за перший місяць. Це тому, що ми заробили відсотки не тільки на оригінальні $1,000, які ми внесли, але ми також заробили відсотки на 2,50 доларів відсотків, які ми заробили в перший місяць. Це ключова перевага, яку дає нам складання інтересу.
Розраховуємо ще кілька місяців:
| Місяць | Стартовий баланс | Зароблені відсотки | Кінцева Баланс |
|---|---|---|---|
| 1 | 1000.00 | 2.50 | 1002.50 |
| 2 | 1002.50 | 2.50 | 1005.01 |
| 3 | 1005.01 | 2.51 | 1007.52 |
| 4 | 1007.52 | 2.52 | 1010.04 |
| 5 | 1010.04 | 2.53 | 1012.57 |
| 6 | 1012.57 | 2.53 | 1015.10 |
| 7 | 1015.10 | 2.54 | 1017.64 |
| 8 | 1017.64 | 2.54 | 1020.18 |
| 9 | 1020.18 | 2.55 | 1022.73 |
| 10 | 1022.73 | 2.56 | 1025.29 |
| 11 | 1025.29 | 2.56 | 1027.85 |
| 12 | 1027.85 | 2.57 | 1030.42 |
Щоб знайти рівняння для представлення цього, якщо\(P_m\) представляє суму грошей через\(m\) місяці, то ми могли б написати рекурсивне рівняння:
\(P_0 = $1000\)
\(P_m = (1+0.0025)P_{m-1}\)
Ви, напевно, визнаєте це як рекурсивну форму експоненціального зростання. Якщо ні, ми могли б пройти кроки, щоб побудувати явне рівняння для зростання:
\(P_0 = $1000\)
\(P_1 = 1.0025P_0 = 1.0025 (1000)\)
\(P_2 = 1.0025P_1 = 1.0025 (1.0025 (1000)) = 1.0025 2 (1000)\)
\(P_3 = 1.0025P_2 = 1.0025 (1.00252 (1000)) = 1.00253 (1000)\)
\(P_4 = 1.0025P_3 = 1.0025 (1.00253 (1000)) = 1.00254 (1000)\)
Спостерігаючи закономірність, ми могли б зробити висновок
\(P_m = (1.0025)^m($1000)\)
Зверніть увагу, що $1000 в рівнянні була\(P_0\), початкова сума. Ми знайшли 1.0025, додавши один до темпу зростання, розділеного на 12, оскільки ми складали 12 разів на рік. Узагальнюючи наш результат, ми могли б написати
\[P_m = P_0 \left(1 + \dfrac{r}{k} \right)^m \nonumber \]
У цій формулі:
- \(m\)кількість періодів компаундирования (місяців у нашому прикладі)
- \(r\)річна процентна ставка
- \(k\)це кількість з'єднань на рік.
Хоча ця формула працює нормально, частіше використовувати формулу, яка включає кількість років, а не кількість періодів складання. \(N\)Якщо число років, то\(m=Nk\). Внесення цієї зміни дає нам стандартну формулу складних відсотків.
\[P_N = P_0 \left(1 + \dfrac{r}{k} \right)^{Nk} \nonumber \]
- \(P_N\)залишок на рахунку через\(N\) роки.
- \(P_0\)початковий залишок рахунку (також називається початковим депозитом, або основним)
- \(r\)річна процентна ставка в десятковій формі
- \(k\)кількість періодів компаундирования в одному році.
Якщо компаундування проводиться щорічно (один раз на рік),\(k = 1\).
Якщо компаундування проводиться щоквартально,\(k = 4\).
Якщо компаундування проводиться щомісяця,\(k = 12\).
Якщо компаундування проводиться щодня,\(k = 365\).
Найголовніше, що потрібно пам'ятати про використання цієї формули, це те, що вона передбачає, що ми поклали гроші на рахунок один раз і нехай сидимо там, заробляючи відсотки.
Депозитний сертифікат (CD) - це ощадний інструмент, який пропонують багато банків. Зазвичай це дає більш високу процентну ставку, але ви не можете отримати доступ до своїх інвестицій протягом певного періоду часу. Припустимо, ви вносите $3000 на компакт-диску, сплачуючи 6% відсотків, що складаються щомісяця. Скільки у вас буде на рахунку через 20 років?
Рішення
У цьому прикладі
Початковий депозит:
\(P_0 = $3000\)
6% річна ставка:
\(r = 0.06\)
12 місяців в 1 році:
\(k = 12\)
Оскільки ми шукаємо, скільки у нас буде через 20 років
\(N = 20\)
Отже,
\(P_{20} = 3000 \left(1 + \dfrac{0.06}{12} \right)^{20 \times 12} = $9930.61\)(округлити відповідь до найближчої копійки)
Давайте порівняємо суму грошей, зароблених від компаундирования, з сумою, яку ви б отримали від простих відсотків.
| Років | Простий відсоток ($15 на місяць) | 6% посилюється щомісяця = 0,5% щомісяця. |
|---|---|---|
| 5 | $3900 | $4046,55 |
| 10 | $4800 | $5458.19 |
| 15 | $5700 | $7362,28 |
| 20 | $6600 | $9930,61 |
| 25 | $7500 | $13394,91 |
| 30 | $8400 | $18067,73 |
| 35 | $9300 | $24370,65 |
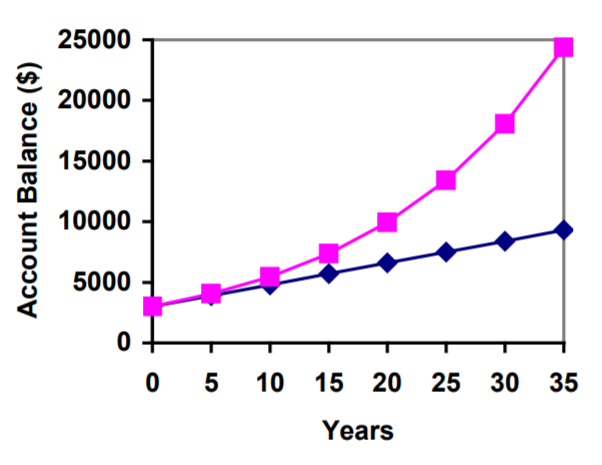
Як бачите, протягом тривалого періоду часу компаундування робить велику різницю в балансі рахунку. Ви можете визнати це як різницю між лінійним зростанням та експоненціальним зростанням.
Коли нам потрібно обчислити щось\(5^3\) подібне, досить просто просто помножити\(5 \cdot 5 \cdot 5=125\). Але коли нам потрібно обчислити щось на кшталт\(1.0052^{40}\), було б дуже нудно обчислити це, помноживши\(1.005\) на себе\(240\) рази! Тож, щоб полегшити ситуацію, ми можемо використати силу наших наукових калькуляторів.
Більшість наукових калькуляторів мають кнопку для експонентів. Зазвичай це або позначено як:
\(^\),\(y^x\), або\(x^y\)
Для оцінки\(1.0052^{40}\) ми б набрати\(1.0052\)\(^\)\(40\), або\(1.0052\)\(y^x\)\(40\). Спробуйте - у вас повинно вийти щось навколо\(3.3102044758\).
Ви знаєте, що вам знадобиться 40 000 доларів на освіту вашої дитини через 18 років. Якщо ваш рахунок заробляє 4% щоквартально, скільки вам потрібно буде внести зараз, щоб досягти своєї мети?
Рішення
У цьому прикладі ми шукаємо\(P_0\).
4%:
\(r = 0.04\)
4 квартали в 1 рік:
\(k = 4\)
Так як ми знаємо баланс в 18 років:
\(N = 18\)
Сума, яку ми маємо в 18 років:
\(P_{18} = $40000\)
У цьому випадку, ми будемо мати, щоб налаштувати рівняння і вирішити для\(P_0\).
\(40000 = P_0 \left(1 + \dfrac{0.04}{4} \right)^{18 \times 4}\)
\(40000 = P_0 \left( 2.0472 \right)\)
\(P_0 = \dfrac{40000}{2.0472} = $19539.84\)
Отже, вам потрібно було б внести депозит\($19,539.84\) зараз, щоб мати\(18\) протягом\($40,000\) багатьох років.
Важливо дуже обережно ставитися до округлення при обчисленні речей з показниками. Загалом, ви хочете зберегти якомога більше десяткових знаків під час обчислень. Обов'язково зберігайте хоча б 3 значущі цифри (числа після будь-яких провідних нулів). Округлення 0.00012345 до 0.000123 зазвичай дає вам «досить близьку» відповідь, але зберігати більше цифр завжди краще.
Причина, по якій ми не повинні «надмірно круглі», відображається в цьому прикладі. Припустимо, ви інвестували 1,000 доларів під 5% відсотків щомісяця протягом 30 років.
Рішення
Початковий депозит:
\(P_0 = $1000\)
5%:
\(r = 0.05\)
12 місяців в 1 році:
\(k = 12\)
Оскільки ми шукаємо суму після 30 років:
\(N = 30\)
Якщо ми спочатку обчислимо\(\dfrac{r}{k}\), ми знаходимо\(\dfrac{0.05}{12} = 0.00416666666667\)
Ось ефект округлення цього до різних значень:
| \(\dfrac{r}{k}\)округляється до: | \(P_{30}\)Дає бути: | Помилка |
|---|---|---|
| \ (\ dfrac {r} {k}\) округлено до: ">0.004 | \ (P_ {30}\) бути: ">$4208.59 | $259.15 |
| \ (\ dfrac {r} {k}\) округлено до: ">0.0042 | \ (P_ {30}\) має бути: ">$4521.45 | $53.71 |
| \ (\ dfrac {r} {k}\) округлено до: ">0.00417 | \ (P_ {30}\) бути: ">$4473.09 | $5.35 |
| \ (\ dfrac {r} {k}\) округлено до: ">0.004167 | \ (P_ {30}\) бути: ">$4468.28 | $0.54 |
| \ (\ dfrac {r} {k}\) округлено до: ">0.0041667 | \ (P_ {30}\) має бути: ">$4467.80 | $0.06 |
| \ (\ dfrac {r} {k}\) округлено до: ">Без округлення | \ (P_ {30}\) має бути: ">$4467.74 |
Якщо ви працюєте в банку, звичайно, ви б взагалі не округлили. Для наших цілей відповідь, яку ми отримали шляхом округлення до\(0.00417\), трьох значущих цифр, досить близький -\($5\) вимкнено\($4,500\) не так вже й погано. Звичайно, збереження цього четвертого знака після коми не зашкодило б.
Використання калькулятора У багатьох випадках ви можете уникнути округлення повністю, як ви вводите речі у свій калькулятор. Наприклад, в прикладі вище нам знадобилося обчислити
\(P_{30} = 1000 \left(1 + \dfrac{0.05}{12} \right)^{12 \times 30}\)
Ми можемо швидко розрахувати\(12 \times 30 = 360\), даючи\(P_{30} = 1000 \left(1 + \dfrac{0.05}{12} \right)^{360}\)
Тепер ми можемо скористатися калькулятором.
| Введіть це | Калькулятор показує |
|---|---|
| \(0.05\; ÷ \;12 \;= \) | 0.004166666667 |
| \(+\; 1\; =\) | 1,004166666667 |
| \(y^x\; 360\; = \) | 4.4677443 1400613 |
| \(\times \; 1000 \;=\) | 4467.74431400613 |
Попередні кроки передбачали, що у вас є калькулятор «одна операція за раз»; більш просунутий калькулятор часто дозволить вам ввести весь вираз, який потрібно оцінити. Якщо у вас є такий калькулятор, вам, ймовірно, просто потрібно буде ввести:
\(1000 \; \times \; (1\; +\; 0.05\; ÷ \;12)\; y^x \;360\; =\)
