2.6: Розв'язування рівнянь

Нагадаємо (див. Розділ 1.6), що змінна є символом (зазвичай буквою), що позначає значення, яке змінюється. Якщо змінна в рівнянні замінюється числом і виходить справжнє твердження, то це число називається розв'язком рівняння.

Приклад 1

Чи є −6 розв'язком рівняння 2x +5= −7?

Рішення

Замініть −6 для x у рівнянні.

\[ \begin{aligned} 2x + 5 = 7 ~ & \textcolor{red}{ \text{ Original equation.}} \\ 2(-6)+5 = -7 ~ & \textcolor{red}{ \text{ Substitute } -6 \text{ for } x.} \\ -12 + 5 = -7 ~ & \textcolor{red}{ \text{ On the left, multiply first.}} \\ -7 = -7 ~ & \textcolor{red}{ \text{ On the left, add.}} \end{aligned}\nonumber \]

Оскільки останній оператор є справжнім твердженням, −6 є розв'язком рівняння.

Вправа

Чи є −4 розв'язком 8 − 2 x = 5?

Відповідь

Ні

Додавання або віднімання однакової суми

Два рівняння, що мають однаковий набір розв'язків, еквівалентні. Наприклад, 2 x +5 = −7 і x = −6 мають однакові розв'язки. Тому вони є рівнозначними рівняннями. Деякі алгебраїчні операції дають еквівалентні рівняння.

Створення еквівалентних рівнянь

Додавання однакової величини до обох сторін рівняння. Якщо почати з рівняння

\[a = b,\nonumber \]

потім додавання c до обох сторін рівняння дає еквівалентне рівняння

\[ a + c = b + c.\nonumber \]

Віднімання однакової величини з обох сторін рівняння. Якщо почати з рівняння

\[a = b,\nonumber \]

потім віднімання c з обох сторін рівняння дає еквівалентне рівняння

\[a − c = b − c.\nonumber \]

Тобто додавання або віднімання однакової кількості з обох сторін рівняння не змінить розв'язків рівняння.

Приклад 2

Розв'язувати для x: x + 3= −7.

Рішення

Щоб скасувати ефект додавання 3, відніміть 3 з обох сторін рівняння.

\[ \begin{aligned} x + 3 = -7 ~ & \textcolor{red}{ \text{ Original equation.}} \\ x + 3 - 3 = -7 -3 ~ & \textcolor{red}{ \text{ Subtract 3 from both sides.}} \\ x = -7 + (-3) ~ & \begin{array}{l} \textcolor{red}{ \text{ Simplify the left hand side. On the right,}} \\ \textcolor{red}{ \text{ express subtractions as adding the opposite.}} \end{array} \\ x = -10 \end{aligned}\nonumber \]

Щоб перевірити розв'язок, підставити −10 для x у вихідному рівнянні та спростити.

\[ \begin{aligned} x + 3 = -7 ~ & \textcolor{red}{ \text{ Original equation.}} \\ -10 + 3 = -7 ~ & \textcolor{red}{ \text{ Substitute } -10 \text{ for } x.} \\ =7 = -7 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]

Оскільки останній рядок перевірки є твердженням true, це підтверджує, що −10 є розв'язком.

Вправа

Вирішити для х: х + 9 = -11.

Відповідь

х = −20

Приклад 3

Розв'язувати для x: x − 8 = −11.

Рішення

Щоб скасувати ефект віднімання 8, додайте 8 до обох сторін рівняння.

\[ \begin{aligned} x - 8 = -11 ~ & \textcolor{red}{ \text{ Original equation.}} \\ x - 8 + 8 = -11+ 8 ~ & \textcolor{red}{ \text{ Add 8 to both sides.}} \\ x = -3 ~ & \textcolor{red}{ \text{ Simplify both equations.}} \end{aligned}\nonumber \]

Щоб перевірити розв'язок, підставити −3 для x у вихідному рівнянні та спростити.

\[ \begin{aligned} x - 8 = -11 ~ & \textcolor{red}{ \text{ Original equation.}} \\ -3 - 8 = -11 ~ & \textcolor{red}{ \text{ Substitute } -3 \text{ for } x.} \\ -11 = -11 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]

Оскільки останній рядок перевірки є твердженням true, це підтверджує, що −3 є розв'язком.

Вправа

Розв'язувати для x: x − 2 = −7

Відповідь

х = −5

Іноді трохи спрощення в порядку, перш ніж почати процес вирішення.

Приклад 4

Розв'язувати для y: −8+2= y − 11 (−4).

Рішення

По-перше, спростити обидві сторони рівняння.

\[ \begin{aligned} -8 + 2 = y -11(-4) ~ & \textcolor{red}{ \text{ Original equation.}} \\ -6 = y -(-44) ~ & \begin{array}{l} \textcolor{red}{ \text{ Simplify. On the left, } -8 + 2 = -6.} \\ \textcolor{red}{ \text{ On the right, } 11(-4) = -44.} \end{array} \\ -6 = y + 44 - 44 ~ & \textcolor{red}{ \text{ Subtract 44 from both sides of the equation.}} \\ -6 + (-44) = y ~ & \textcolor{red}{ \text{ Express subtraction as addition. Simplify on the right.}} \\ -50 = y \end{aligned}\nonumber \]

Щоб перевірити розв'язку, замініть −50 для y у вихідному рівнянні та спростити.

\[ \begin{aligned} -8 + 2 = y -11(-4) ~ & \textcolor{red}{ \text{ Original equation.}} \\ -8 + 2 = -50 -11 (-4) ~ & \textcolor{red}{ \text{ Substitute } -50 \text{ for } y.} \\ -6 = -50 -(-44) ~ & \textcolor{red}{ \text{ Express subtraction on the right as addition.}} \\ -6 = -6 ~ & \textcolor{red}{ \text{ On the right, add: } -50 + 44 = -6.} \end{aligned}\nonumber \]

Оскільки останній рядок перевірки є твердженням true, це підтверджує, що −50 є розв'язком.

Вправа

Розв'язок для y: y + 2 (−4) = −8+6

Відповідь

у = 6

Множення або ділення на ту саму суму

Додавання та віднімання - не єдиний спосіб отримання еквівалентного рівняння.

Створення еквівалентних рівнянь

Множення обох сторін рівняння на однакову величину. Якщо почати з рівняння

\[a = b,\nonumber \]

потім множення обох сторін рівняння на c дає еквівалентне рівняння

\[ a \cdot c = b \cdot c, \text{ or equivalently, } ac = bc,\nonumber \]

за умови c ≠ 0.

Розділення обох сторін рівняння на однакову величину. Якщо почати з рівняння

\[ a = b,\nonumber \]

потім діливши обидві сторони рівняння на c, виходить еквівалентне рівняння

\[ \frac{a}{c} = \frac{b}{c},\nonumber \]

за умови c ≠ 0.

Тобто множення або ділення обох сторін рівняння на однакову величину не змінить розв'язків рівняння.

Приклад 5

Розв'язувати для x: −3 x = 30.

Рішення

Щоб скасувати ефект множення на −3, розділіть обидві сторони рівняння на −3.

\[ \begin{aligned} -3x = 30 ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{-3x}{-3} = \frac{30}{-3} ~ & \textcolor{red}{ \text{ Divide both sides by }-3.} \\ x = -10 ~ & \begin{array}{l} \textcolor{red}{ \text{ On the left, } -3 \text{ times } x, \text{ divided by } -3 \text{ is } x.} \\ \textcolor{red}{ \text{ On the right, } 30/(-3)=-10.} \end{array} \end{aligned}\nonumber \]

Щоб перевірити розв'язок, підставити −10 для x у вихідному рівнянні та спростити.

\[ \begin{aligned} -3x = 30 ~ & \textcolor{red}{ \text{ Original equation.}} \\ -3(-10) = 30 ~ & \textcolor{red}{ \text{ Substitute } -10 \text{ for } x.} \\ 30 - 30 ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Оскільки останній рядок перевірки є твердженням true, це підтверджує, що −10 є розв'язком.

Вправа

Розв'язувати для z: −4z = −28

Відповідь

z = 7

Приклад 6

Вирішити для х:\( \frac{x}{-2} = -20\).

Рішення

Щоб скасувати ефект ділення на −2, помножте обидві сторони рівняння на −2.

\[ \begin{aligned} \frac{x}{-2} = -20 ~ & \textcolor{red}{ \text{ Original equation.}} \\ -2 \left( \frac{x}{-2} \right) - -2 (-20) ~ & \textcolor{red}{ \text{ Multiply both sides by } -2.} \\ x = 40 ~ & \begin{array}{l} \textcolor{red}{ \text{ On the left, } x \text{ divided by } -2, \text{ multiplied by } -2,} \\ \textcolor{red}{ \text{ the result is } x. \text{ On the right, } -2(-20) = 40.} \end{array} \end{aligned}\nonumber \]

Щоб перевірити рішення, підставимо 40 на x у вихідному рівнянні і спрощуємо.

\[ \begin{aligned} \frac{x}{-2} = -20 ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{40}{-2} = -20 ~ & \textcolor{red}{ \text{ Substitute 40 for } x.} \\ -20 = -20 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]

Оскільки останній рядок перевірки є істинним твердженням, це підтверджує, що 40 - це рішення.

Комбінування операцій

Нагадаємо обговорення «Wrap» та «Unwrap» з розділу 1.6. Щоб обернути подарунок, ми: (1) одягаємо подарунковий папір, (2) одягаємо стрічку і (3) надягаємо декоративний бант. Щоб розгорнути подарунок, ми повинні «скасувати» кожен з цих кроків у зворотному порядку. Отже, щоб розгорнути подарунок, ми: (1) знімаємо декоративний бантик, (2) знімаємо стрічку і (3) знімаємо подарунковий папір.

Тепер уявіть собі машину, яка приймає його вхід, потім: (1) множить вхід на 2, а (2) додає 3 до результату. Ця машина зображена зліва на малюнку 2.16.

Малюнок 2.16: Друга машина «розкручує» першу машину.

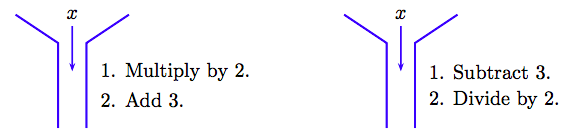
Щоб «розгорнути» ефект машини зліва, нам знадобиться машина, яка буде «скасовувати» кожен з кроків першої машини, але в зворотному порядку. Машина «розгортання» зображена праворуч на малюнку 2.16. Він спочатку відніме три з його вхідних даних, потім розділить результат на 2. Зверніть увагу, що кожна з цих операцій «скасовує» відповідну роботу першої машини, але в зворотному порядку.

Наприклад, опустіть ціле число 7 в першу машину зліва на малюнку 2.16. Спочатку подвоюємо 7, потім додаємо 3 до результату. В результаті виходить 2 (7) + 3 = 17.

Тепер, щоб «розгорнути» цей результат, скидаємо 17 в другу машину. Спочатку віднімаємо 3, потім ділимо на 2. Результатом є (17 − 3) /2 = 7, початкове ціле число, введене в першу машину.

Тепер розглянемо рівняння

\[2x +3=7.\nonumber \]

Зліва порядок операцій вимагає, щоб ми спочатку помножимо х на 2, потім додаємо 3. Щоб вирішити це рівняння для x, ми повинні «скасувати» кожну з цих операцій у зворотному порядку. Таким чином, ми (1) віднімемо три з обох сторін рівняння, потім (2) розділимо обидві сторони отриманого рівняння на 2.

\[ \begin{aligned} 2x + 3 - 3 = 7 - 3 ~ & \textcolor{red}{ \text{ Subtract 3 from both sides.}} \\ 2x = 4 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ \frac{2x}{2} = \frac{4}{2} ~ & \textcolor{red}{ \text{ Divide both sides by 2.}} \\ x = 2 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]

Читачі повинні перевірити це рішення у вихідному рівнянні.

Приклад 7

Вирішити для х:\(\frac{x}{4} - 3 = -7\).

Рішення

Ліворуч порядок операцій вимагає, щоб ми спочатку ділимо х на 4, потім віднімаємо 3. Щоб вирішити це рівняння для x, ми повинні «скасувати» кожну з цих операцій у зворотному порядку. Таким чином, ми (1) додамо 3 до обох сторін рівняння, потім (2) помножимо обидві сторони отриманого рівняння на 4.

\[ \begin{aligned} \frac{x}{4} - 3 = -7 ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{x}{4} - 3 + 3 = -7 + 3 ~ & \textcolor{red}{ \text{ Add 3 to both sides.}} \\ \frac{x}{4} = -4 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ 4 \left( \frac{x}{4} \right) = 4 (-4) ~ & \textcolor{red}{ \text{ Multiply both sides by 4.}} \\ x = -16 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]

Перевірити

Замініть −16 для x у вихідному рівнянні.

\[ \begin{aligned} \frac{x}{4} - 3 = 7 ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{-16}{4} - 3 = -7 ~ & \textcolor{red}{ \text{ Substitute } -16 \text{ for } x.} \\ -4 -3 = -7 ~ & \textcolor{red}{ \text{ Divide first: } -16/4 = -4.} \\ -7 = - 7 ~ & \textcolor{red}{ \text{ Subtract: } -4 -3 = -7.} \end{aligned}\nonumber \]

Оскільки останній рядок перевірки є твердженням true, −16 є розв'язком вихідного рівняння.

Вправа

Вирішити для х:

\[ \frac{x}{2} + 6 = 4\nonumber \]

Відповідь

х = -4

Приклад 8

Розв'яжіть для t: 0=8 − 2 т.

Рішення

Праворуч порядок операцій вимагає спочатку помножити t на −2, потім додати 8. Щоб вирішити це рівняння для t, ми повинні «скасувати» кожну з цих операцій у зворотному порядку. Таким чином, ми (1) віднімемо 8 з обох сторін рівняння, потім (2) розділимо обидві сторони отриманого рівняння на −2.

\[ \begin{aligned} 0 = 8 -2t ~ & \textcolor{red}{ \text{ Original equation.}} \\ 0 - 8 = 8 - 2t - 8 ~ & \textcolor{red}{ \text{ Subtract 8 from both sides.}} \\ -8 = -2t ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ \frac{-8}{-2} = \frac{-2t}{-2} ~ & \textcolor{red}{ \text{ Divide both sides by 2.}} \\ 4 = t ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]

Перевірити

Замініть 4 для t у вихідному рівнянні.

\[ \begin{aligned} 0 = 8 - 2t ~ & \textcolor{red}{ \text{ Original equation.}} \\ 0 = 8 - 2(4) ~ & \textcolor{red}{ \text{ Substitute 4 for } t.} \\ 0 = 8-8 ~ & \textcolor{red}{ \text{ Multiply first: 2(4) = 8.}} \\ 0 = 0 ~ & \textcolor{red}{ \text{ Subtract: } 8-8=0.} \end{aligned}\nonumber \]

Оскільки останній рядок у перевірці є істинним твердженням, 4 є розв'язком вихідного рівняння.

Вправа

Вирішити для r: 0 = 9 + 3 р

Відповідь

р = -3

Приклад 9

Вирішити для p:\(-12 + 3 = -8+4 + \frac{p}{-3}.\)

Рішення

Завжди спрощуйте, коли це можливо.

\[ \begin{aligned} -12+3= -8+4+ \frac{p}{-3} ~ & \textcolor{red}{ \text{ Origianl equation.}} \\ -9 = -4 + \frac{p}{-3} ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]

Праворуч порядок операцій вимагає спочатку розділити p на −3, потім додати −4. Щоб вирішити це рівняння для p, ми повинні «скасувати» кожну з цих операцій у зворотному порядку. Таким чином, ми (1) додамо додатне 4 до обох сторін рівняння, а потім (2) помножимо обидві сторони отриманого рівняння на −3.

\[ \begin{aligned} -9+-4 = -4+ \frac{p}{-3} + 4~ & \textcolor{red}{ \text{ Add 4 to both sides.}} \\ -5 = \frac{p}{-3} ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ -3(-5) = -3 \left( \frac{p}{-3} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by } -3.} \\ 15 = p ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]

Перевірити

Замініть 15 для p у вихідному рівнянні.

\[ \begin{aligned} -12 + 3 = =8 + 4 + \frac{p}{-3} ~ & \textcolor{red}{ \text{ Original equation.}} \\ -12 + 3 = -8 + 4 + \frac{15}{-3} ~ & \textcolor{red}{ \text{ Substitute 15 for } p.} \\ -9 = -8 + 4 + (-5) ~ & \begin{aligned} \textcolor{red}{ \text{ On the left, add: } -12 + 3 = -9. \text{ On the }} \\ \textcolor{red}{ \text{ right, divide: } 15/(-3) = -5.} \end{aligned} \\ -9 = -4 + (-5) ~ & \textcolor{red}{ \text{ On the right, } -8 + 4 = -4.} \\ -9 = -9 ~ & \textcolor{red}{ \text{ On the right, add: } -4 + (-5) = -9.} \end{aligned}\nonumber \]

Оскільки останній рядок у перевірці є істинним твердженням, 15 - це рішення вихідного рівняння.

Вправа

Вирішити для q:

\[ \frac{q}{-2} -9 = -8+3\nonumber \]

Відповідь

q = −8

Додатки

Давайте розглянемо деякі програми рівнянь, що включають цілі числа. По-перше, ми нагадуємо читачам, що рішення проблеми слова повинно включати в себе кожен з наступних кроків.

Вимоги до вирішення проблем Word

1. Налаштуйте словник змінних. Ви повинні повідомити своїм читачам, що представляє кожна змінна у вашій проблемі. Це може бути досягнуто кількома способами:
   1. Такі заяви, як «Нехай P представляє периметр прямокутника».
   2. Позначення невідомих значень змінними в таблиці.
   3. Маркування невідомих величин в ескізі або схемі.
2. Налаштуйте рівняння. Кожне рішення проблеми зі словом має містити ретельно розроблене рівняння, яке точно описує обмеження в постановці задачі.
3. Розв'яжіть рівняння. Ви завжди повинні вирішувати рівняння, встановлене на попередньому кроці.
4. Дайте відповідь на питання. Цей крок легко не помітити. Наприклад, проблема може запитати вік Джейн, але рішення вашого рівняння дає вік сестри Джейн Ліз. Переконайтеся, що ви відповіли на оригінальне запитання, поставлене в проблемі. Ваше рішення має бути записано в реченні з відповідними одиницями.
5. Озирніться назад. Важливо зазначити, що цей крок не означає, що ви повинні просто перевірити своє рішення у своєму рівнянні. Зрештою, можливо, ваше рівняння неправильно моделює ситуацію задачі, тож ви можете мати правильне рішення неправильного рівняння. Важливе питання: «Чи має сенс ваша відповідь на основі слів в оригінальній постановці проблеми».

приклад 10

Банківський рахунок студента переоформляється. Зробивши свій рахунок, Аллен виявляє, що він перемальований на 15 доларів. Яким був баланс його рахунку до його зняття? депозит $120, він виявляє, що його рахунок все ще перемальований на суму $75. Яким був його баланс до того, як він зробив свій депозит?

Рішення

У нашому рішенні ми розглядаємо кожен крок Вимоги до вирішення проблем Word.

1. Налаштуйте словник змінних. В даному випадку невідомим є початковий залишок на рахунку учня. Нехай B представляють цей початковий баланс.

2. Налаштуйте рівняння. Позитивне ціле число являє собою здоровий баланс, а від'ємне число - рахунок, який перемальований. Після депозиту студента рахунок все ще перемальовується на 75 доларів. Ми скажемо, що цей баланс становить −75 доларів. Таким чином,

\[ \begin{array}{c c c c c} \colorbox{cyan}{Original Balance} & \text{plus} & \colorbox{cyan}{Student Deposit} & \text{equals} & \colorbox{cyan}{Current Balance} \\ B & + & $120 & = & -$75 \end{array}\nonumber \]

3. Розв'яжіть рівняння. Щоб «скасувати» додавання, відніміть 120 з обох сторін рівняння.

\[ \begin{aligned} B + 120 = -75 ~ & \textcolor{red}{ \text{ Original equation.}} \\ B + 120 - 120 = -75 - 120 ~ & \textcolor{red}{ \text{ Subtract 120 from both sides.}} \\ B = -195 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]

4. Дайте відповідь на питання. Початковий баланс був перемальований на суму 195 доларів.

5. Озирніться назад. Якщо початковий баланс був перекреслений на $195, то ми дозволимо −$195 представляти цей баланс. Студент вносить депозит у розмірі 120 доларів. Додайте це до початкового балансу, щоб отримати −$195 + $120 = −$75, правильний поточний баланс.

Вправа

Після зняття 125 доларів зі свого рахунку Аллен виявляє, що він передрахований на 15 доларів. Яким був баланс його рахунку до його зняття?

Відповідь

$110

Приклад 11

Три більше, ніж удвічі певне число - −11. Знайдіть невідомий номер.

Рішення

У нашому рішенні ми розглядаємо кожен крок Вимоги до вирішення проблем Word.

1. Налаштуйте словник змінних. Нехай x представляють невідоме число. 2. Налаштуйте рівняння. «Три більше двох разів певне число» стає:

\[ \begin{array}{c c c c c} \colorbox{cyan}{Three} & \text{more than} & \colorbox{cyan}{Twice a Certain Number} & \text{is} & \colorbox{cyan}{-11} \\ 3 & + & 2x & = & 11 \end{array}\nonumber \]

3. Розв'яжіть рівняння. Зліва порядок операцій вимагає, щоб ми спочатку помножимо х на 2, потім додаємо 3. Щоб вирішити це рівняння для x, ми повинні «скасувати» кожну з цих операцій у зворотному порядку. Таким чином, ми (1) віднімемо 3 з обох сторін рівняння, потім (2) розділимо обидві сторони отриманого рівняння на 2.

\[ \begin{aligned} 3 + 2x = -11 ~ & \textcolor{red}{ \text{ Original equation.}} \\ 3 + 2x - 3 = -11 - 3 ~ & \textcolor{red}{ \text{ Subtract 3 from both sides.}} \\ 2x = -14 ~ & \textcolor{red}{ \text{ Simplify both sides.}} ~ \\ \frac{2x}{2} = \frac{-14}{2} ~ & \textcolor{red}{ \text{ Divide both sides by 2.}} \\ x = -7 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]

4. Дайте відповідь на питання. Невідомим числом є −7.

5. Озирніться назад. Чи задовольняє відповідь проблемним обмеженням? На три більше, ніж двічі −7, на три більше ніж −14, або −11. Так що рішення правильне.

Вправа\(\PageIndex{1}\)

На п'ять менше ніж удвічі певне число дорівнює −7. Знайдіть невідомий номер.

Відповідь

−1

Вправи

1. Чи є −11 розв'язком 2x +3= −19?

2. Чи є −8 розв'язком 2x +7= −9?

3. Чи є 6 розчином 3х+ 1 = 19?

4. Чи є −6 розв'язком 2x +7= −5?

5. Чи є 12 розчином 4x +5= −8?

6. Чи є −8 розв'язком −3x + 8 = 18?

7. Чи є 15 розчином 2x +6= −9?

8. Чи є 3 розв'язком −4x +1= −20?

9. Чи є −15 розв'язком −3x +6= −17?

10. Чи є −18 розв'язком −3x +9= −9?

11. Чи є −6 розв'язком −2x + 3 = 15?

12. Чи є 7 розв'язком −3x +5= −16?

---

У вправах 13-28 розв'яжіть задане рівняння для x.

13. х − 13 = 11

14. х − 6 = 12

15. x − 3=6

16. х − 3 = −19

17. х + 10 = 17

18. х +3=9

19. x − 6=1

20. х − 10 = 12

21. х − 15 = −12

22. х − 2 = 13

23. х + 11 = −19

24. х + 3 = 17

25. х +2=1

26. х +2= −20

27. х +5= −5

28. х + 14 = −15

---

У вправах 29-44 розв'яжіть задане рівняння для x.

29. −х = −20

30. 5х = −35

31. \(\frac{x}{−7}\)= 10

32. \(\frac{x}{−6}\)= −20

33. \(\frac{x}{−10}\)= 12

34. \(\frac{x}{2}\)= 11

35. \(\frac{x}{9}\)= −16

36. \(\frac{x}{−3}\)= −7

37. −10х = 20

38. −17х = −85

39. 14х = 84

40. −10х = −40

41. −2х = 28

42. −14х = 42

43. \(\frac{x}{−10}\)= 15

44. \(\frac{x}{−8}\)= −1

---

У вправах 45-68 розв'яжіть задане рівняння для х.

45. −4х − 4 = 16

46. −6х − 14 = 4

47. 4х − 4 = 76

48. −5х − 15 = 45

49. 5х− 14 = −79

50. 15х − 2 = 43

51. −10х − 16 = 24

52. 2х− 7 = −11

53. 9х +5= −85

54. 8х +8= −16

55. 7х+15 = −55

56. 2х+2= −38

57. −х + 8 = 13

58. −5х + 20 = −50

59. 12х − 15 = −3

60. −19х − 17 = −36

61. 4х − 12 = −56

62. 7х− 16 = 40

63. 19х + 18 = 113

64. −6х + 20 = −64

65. −14х + 12 = −2

66. −9х + 5 = 104

67. 14х + 16 = 44

68. −14х + 10 = −60

---

69. У два менше восьми разів невідоме число становить −74. Знайдіть невідомий номер.

70. У шість менше трьох разів невідоме число дорівнює 21. Знайдіть невідомий номер.

71. У вісім більше двох разів невідоме число дорівнює 0. Знайдіть невідомий номер.

72. П'ять більше ніж у вісім разів невідоме число дорівнює −35. Знайдіть невідомий номер.

73. Число −6 на 2 більше, ніж невідоме число. Знайдіть невідомий номер.

74. Число −4 на 7 більше, ніж невідоме число. Знайдіть невідомий номер.

75. У три більше восьми разів невідоме число становить −29. Знайдіть невідомий номер.

76. Чотири більше дев'яти разів невідоме число - 85. Знайдіть невідомий номер.

77. Оцінки Алана на його перших трьох іспитах - 79, 61 і 54. Що повинен забити Алан на своєму наступному іспиті в середньому 71 для всіх чотирьох іспитів?

78. Бали Бенні на його перших трьох іспитах 54, 68 і 54. Що повинен забити Бенні на своєму наступному іспиті в середньому 61 для всіх чотирьох іспитів?

79. Частка двох цілих чисел дорівнює 5. Одне з цілих чисел — −2. Знайдіть інше ціле число.

80. Частка двох цілих чисел дорівнює 3. Одне з цілих чисел — −7. Знайдіть інше ціле число.

81. Частка двох цілих чисел дорівнює 9. Одне з цілих чисел — −8. Знайдіть інше ціле число.

82. Частка двох цілих чисел дорівнює 9. Одне з цілих чисел — −2. Знайдіть інше ціле число.

83. Число −5 на 8 більше, ніж невідоме число. Знайдіть невідомий номер.

84. Число −6 на 8 більше, ніж невідоме число. Знайдіть невідомий номер.

85. Банківський рахунок студента переоформляється. Зробивши депозит у розмірі 260 доларів, він виявляє, що його рахунок все ще перемальований на суму 70 доларів. Яким був його баланс до того, як він зробив свій депозит?

86. Банківський рахунок студента переоформляється. Зробивши депозит у розмірі 300 доларів, він виявляє, що його рахунок все ще перемальований на суму 70 доларів. Яким був його баланс до того, як він зробив свій депозит?

87. Банківський рахунок студента переоформляється. Зробивши депозит у розмірі 360 доларів, він виявляє, що його рахунок все ще перемальований на суму 90 доларів. Яким був його баланс до того, як він зробив свій депозит?

88. Банківський рахунок студента переоформляється. Зробивши депозит у розмірі 260 доларів, він виявляє, що його рахунок все ще перемальований на суму $50. Яким був його баланс до того, як він зробив свій депозит?

89. Число −10 у −5 разів більше, ніж невідоме число. Знайдіть невідомий номер.

90. Число −3 у −3 рази більше, ніж невідоме число. Знайдіть невідомий номер 91. Число −15 у −5 разів більше, ніж невідоме число. Знайдіть невідомий номер.

92. Число −16 у 4 рази більше, ніж невідоме число. Знайдіть невідомий номер.

93. У два менше дев'яти разів невідоме число - 7. Знайдіть невідомий номер.

94. У чотири менше двох разів невідоме число дорівнює 8. Знайдіть невідомий номер.

95. Оцінка Марка на його перших трьох іспитах - 79, 84 та 71. Що повинен Марк набрати на своєму наступному іспиті в середньому 74 для всіх чотирьох іспитів?

96. Оцінки Алана на його перших трьох іспитах - 85, 90 та 61. Що повинен забити Алан на своєму наступному іспиті в середньому 77 для всіх чотирьох іспитів?

---

Відповіді

1. Так

3. Так

5. Ні

7. Ні

9. Ні

11. Так

13. 24

15. 9

17. 7

19. 7

21. 3

23. −30

25. −1

27. −10

29. 20

31. −70

33. −120

35. −144

37. −2

39. 6

41. −14

43. −150

45. −5

47. 20

49. −13

51. −4

53. −10

55. −10

57. −5

59. 1

61. −11

63. 5

65. 1

67. 2

69. −9

71. −4

73. −8

75. −4

77. 90

79. −10

81. −72

83. −13

85. -330 дол. США

87. −450 дол. США

89. 2

91. 3

93. 1

95. 62