2.1: Вступ до цілих чисел
- Page ID
- 57317
Як ми бачили у вступі до глави, негативні числа мають багату і багатоповерхову історію. Одне з найбільш ранніх застосувань негативних чисел стосувалося кредитів і дебетів. Наприклад, якщо $5 являє собою кредит або прибуток, то −$5 означає дебет або збиток. Звичайно, у стародавніх була інша грошова система, ніж наша, але ідея виходить. Зауважте, що якщо постачальник отримує прибуток у розмірі 5 доларів США від продажу, то збиток у розмірі −5 доларів при повторному продажі, постачальник виходить з ладу. Тобто сума $5 і −$5 дорівнює нулю. Багато в чому так само кожне ціле число має протилежний або негативний аналог.
Протилежне або негативне цілого числа
Для кожного цілого числа a існує унікальне число − a, яке називається протилежним або від'ємним від a, таке, що a + (− a) = 0.
Протилежне або від'ємне будь-якого цілого числа легко розташовується на числовому рядку.
Розташування числових рядків
Щоб знайти протилежне (або від'ємне) будь-якого цілого числа, спочатку знайдіть ціле число на числовому рядку. Протилежним є відображення цілого числа через початок (нуль).
Приклад 1
Знайдіть ціле число 5 і його протилежне (негативне) на числовому рядку.
Рішення
Намалюйте цифру, а потім нанесіть ціле число 5 на лінії як затінену крапку.
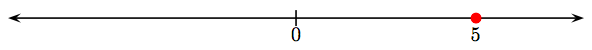
Щоб знайти його протилежність, відобразіть число 5 через походження. Це буде розташування протилежного (негативного) цілого числа 5, яке ми вказуємо символом −5.
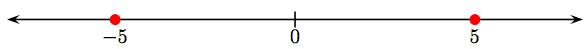
Зверніть увагу на симетрію. Ціле число 5 розташовується на п'яти одиницях праворуч від нуля. Його мінус розташовується на п'яти одиницях зліва від нуля.
Вправа
Знайдіть цифру -7 і її протилежність на цифровому рядку.
Важлива вимова
Символ −5 вимовляється одним із двох способів: (1) «негативна п'ятірка» або (2) «протилежна п'яти».
Подібним чином ми можемо знайти протилежне або негативне будь-якого цілого числа, відображаючи ціле число через початок (нуль), що призводить до зображення, показаного на малюнку 2.1.
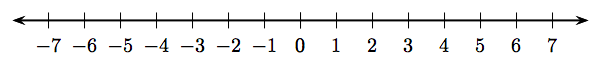
Цілі числа
Колекція чисел, розташованих на числовому рядку на малюнку 2.1, поширюється на невизначений термін вправо, і оскільки цифри зліва є відображеннями через початок, числа також продовжуються на невизначений термін вліво. Ця колекція чисел називається множиною цілих чисел.
Цілі числа
Нескінченна колекція чисел
{..., −7, −6, −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, 6, 7,...}
називається множиною цілих чисел.
Три крапки... на кожному кінці цієї нескінченної збірки означає «etcetera», оскільки цілі числа тривають нескінченно праворуч і ліворуч. Так, наприклад, 23 456 і −117, 191 є елементами цієї множини і тому є цілими числами.
Впорядкування цілих чисел
Як ми бачили з цілими числами, коли ви рухаєтеся вправо на числовому рядку, числа стають більшими; при русі вліво числа стають меншими.
Замовлення на номерному рядку
Нехай a і b - цілі числа, розташовані на числовому рядку так, щоб точка, що представляє ціле число a, лежить ліворуч від точки, що представляє ціле число b.

Тоді ціле число a «менше» ціле число b і пишемо
\[ a < b\nonumber \]
Крім того, ми можемо також сказати, що ціле число b «більше» ціле число a і записати
\[ b > a.\nonumber \]
Приклад 3
Замініть кожне затінене поле на < (less than) or > (більше, ніж), так що результуюча нерівність є істинним твердженням.

Рішення
Для першого випадку знайдіть −3 і 5 на числовому рядку як затінені точки.
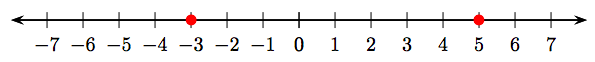
Зауважте, що −3 лежить ліворуч від 5, отже:
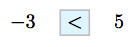
Тобто, −3 дорівнює «менше» 5.
У другому випадку знайдіть −2 та −4 як затінені точки на числовому рядку.
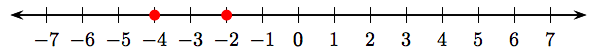
Зауважте, що −2 лежить праворуч від −4, отже:

Тобто, −2 є «більшим за» −4.
Вправа
Порівняйте −12 та −11.
- Відповідь
-
−12 < −11
Важливе спостереження
У прикладі 3 зверніть увагу, що «загострений кінець» символу нерівності завжди вказує на меншу кількість.
Раніше ми заявляли, що кожне ціле число має унікальне число, яке називається його «протилежне» або «негативне». Таким чином, ціле число −5 є протилежним (від'ємним) цілого числа 5. Таким чином, можна сказати, що пара −5 і 5 є протилежностями. Кожен протилежний іншому. Логічно, це призводить нас до висновку, що протилежність −5 дорівнює 5. У символах ми б писали
\[ -(-5) = 5.\nonumber \]
Протилежності протилежностей
Дозвольте a бути цілим числом. Тоді «протилежність протилежному a - це a». В символах пишемо
\[ -(-a) = a.\nonumber \]
Ми також можемо констатувати, що «негатив негативного a» є a.
Приклад 4
Спростити − (−13) та − (−119).
Рішення
Протилежність протилежному числу повертає початкове число. Тобто,
− (−13) = 13 і − (−119) = 11.
Вправа
Спростити: − (−50).
- Відповідь
-
50
Позитивні і негативні
Тепер ми визначаємо терміни додатне ціле і від'ємне ціле число.
Натуральне ціле
Якщо a - ціле число, яке лежить праворуч від нуля (походження) на числовому рядку, то a - натуральне число. Це означає, що a є додатним цілим числом тоді і тільки тоді, коли a > 0.
Таким чином, 2, 5 і 117 є додатними цілими числами.
Негативне ціле
Якщо a - ціле число, яке лежить ліворуч від нуля (походження) на числовому рядку, то a є від'ємним цілим числом. Це означає, що a є від'ємним цілим числом тоді і тільки тоді, коли < 0.
Таким чином, −4, −8 та −1, 123 є від'ємними цілими числами.
Нуль
Ціле нуль не є ні додатним, ні від'ємним.
Приклад 5
Класифікуйте кожне з наступних чисел як від'ємне, додатне або жодне: 4, −6 та 0.
Рішення
Знайдіть 4, −6 та 0 у цифровому рядку.

Таким чином:
- 4 лежить праворуч від нуля. Тобто, 4 > 0, роблячи 4 натуральним цілим числом.
- −6 лежить ліворуч від нуля. Тобто −6 < 0, що робить −6 від'ємним цілим числом.
- Число 0 є нейтральним. Він не є ні негативним, ні позитивним.
Вправа
Класифікувати −11 як позитивний, негативний або ні.
- Відповідь
-
Негативний
Абсолютна величина
Визначимо абсолютне значення цілого числа.
Абсолютна величина
Абсолютне значення цілого числа визначається як його відстань від початку (нуля).
Важливо зазначити, що відстань завжди є невід'ємною величиною (не від'ємною); тобто відстань або додатна, або нульова. Як приклад, ми затінювали цілі числа −4 та 4 на числовому рядку.
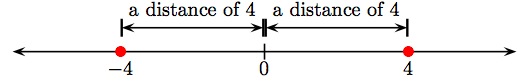
У цифровому рядку вище показано два випадки:
- Ціле число −4 дорівнює 4 одиницям від нуля. Тому що абсолютне значення вимірює відстань від нуля, | − 4| = 4.
- Ціле число 4 також дорівнює 4 одиницям з нуля. Знову ж таки, абсолютне значення вимірює відстань від нуля, тому |4| = 4.
Давайте розглянемо інший приклад.
Приклад 6
Визначте значення кожного виразу: a) | − 7|, b) |3| та c) |0|.
Рішення
Абсолютне значення будь-якого цілого числа дорівнює відстані, яке число знаходиться від початку (нуля) на числовому рядку. Таким чином:
а) Ціле число −7 дорівнює 7 одиницям від початку; отже, | − 7| = 7.
б) Ціле число 3 дорівнює 3 одиницям від початку; отже, |3| = 3.
в) Ціле число 0 дорівнює 0 одиницям від початку; отже, |0| =0.
Вправа
Спрощення: | − 33|.
- Відповідь
-
33
Приклад 7
Визначте значення кожного виразу: a) − (−8) та b) −| − 8|
Рішення
Це чітко різні проблеми.
а) Протилежним параметром −8 є 8. Тобто − (−8) = 8.
б) Однак у цьому випадку ми спочатку беремо абсолютне значення −8, яке дорівнює 8, а потім протилежне цьому результату, щоб отримати −8. Тобто,
\[ \begin{aligned} - | -8 | = -(8) & \textcolor{red}{ \text{ First: } |-8| = 8.} \\ = -8 ~ & \textcolor{red}{ \text{ Second: The opposite of 8 is } -8.} \end{aligned}\nonumber \]
Вправа
Спрощення: −| − 50|.
- Відповідь
-
50
Додатки
Існує ряд додатків, які виграють від використання цілих чисел.
Приклад 8
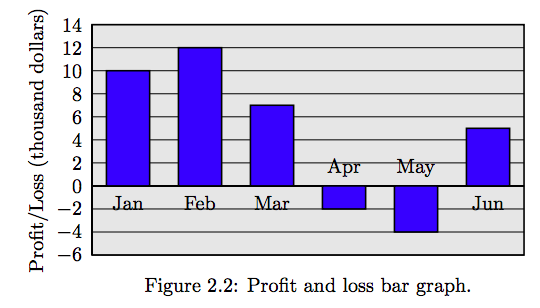
Прибутки і збитки за перші шість місяців фінансового року для малого бізнесу наведені в таблиці 2.1. Прибутки і збитки вимірюються тисячами доларів. Позитивне число являє собою прибуток, а негативне - збиток. Створіть гістограму, що відображає прибутки і збитки для цього малого бізнесу за кожен місяць першої половини фінансового року.
| Місяць | Січ | лют. | бер. | Квітень | Травень | черв. |
| Прибуток/збиток | 10 | 12 | 7 | -2 | -4 | 5 |
Таблиця 2.1: Прибуток і збиток вимірюються тисячами доларів.
Рішення
Почніть з маркування горизонтальної осі місяцями фінансового року. Після виконання цього завдання масштабуйте вертикальну вісь відповідно до значень прибутку/збитків, записаних у таблиці 2.1. Нарешті, починаючи з рівня 0 на горизонтальній осі, накидайте бари, що мають висоту, рівну прибутку і збитку за кожен місяць.
Вправа
Наступна таблиця містить рекордно низькі температури (градуси за Фаренгейтом) для Джексон-Хоул, штат Вайомінг за вказані місяці.
| Місяць | Темп |
| Вересень. | 14 |
| Жовтень. | 2 |
| Лис. | −27 |
| Груд. | −49 |
| Січ. | −50 |
Створіть гістограми температури в порівнянні з місяцями.
Приклад 9
Таблиця 2.2 містить записи низької температури (градуси за Фаренгейтом) п'ять днів поспіль у Фербенксі, Аляска, 1995. Створіть лінійний графік для даних у таблиці 2.2.
| Дата | 21 січ | 22 січ | 23 січ | 24 січ | 25 січ |
| Низька температура | 1 | 10 | 5 | −20 | −28 |
Рішення
Почніть з маркування горизонтальної осі днями січня, коли відбулися температури. Масштабуйте вертикальну вісь відповідно до температур, наведених у таблиці 2.2. Нарешті, сюжет вказує на кожен день на висоті, яка дорівнює температурі для цього дня. З'єднайте послідовні пари точок з відрізками ліній, щоб отримати лінійний графік, показаний на малюнку 2.3.
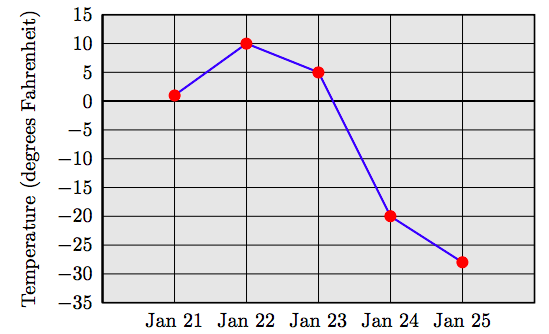
Зверніть увагу, що точки на малюнку 2.3 мають висоти, більші за нуль для 21-23 січня, представляючи температуру більше нуля. Точки, що представляють 24-45 січня, мають негативні висоти, відповідні негативним температурам таблиці 2.2.
Вправа
Чоловік стоїть на даху багатоповерхового будинку і кидає бейсбол вертикально вгору. Висота (в футах) кулі над краєм даху в виміряний час (в секундах) наведена в наступній таблиці.
| Час | Висота |
| 0 | 0 |
| 1 | 24 |
| 2 | 16 |
| 3 | −24 |
| 4 | −96 |
Створіть лінійний графік висоти кулі проти часу в повітрі.
Вправи
У Вправи 1-12 для кожного з наступних питань надайте ескіз числового рядка з вашою відповіддю.
1. Яке число лежить на трьох одиницях ліворуч від 4 на числовому рядку?
2. Яке число лежить на трьох одиницях ліворуч від 1 на числовому рядку?
3. Яке число лежить на трьох одиницях ліворуч від 6 на числовому рядку?
4. Яке число лежить на чотирьох одиницях ліворуч від −2 на числовому рядку?
5. Яке число лежить на двох одиницях праворуч від 0 на числовому рядку?
6. Яке число лежить на чотирьох одиницях праворуч від −2 на числовому рядку?
7. Яке число лежить дві одиниці праворуч від 1 на числовому рядку?
8. Яке число лежить на двох одиницях праворуч від −4 на числовому рядку?
9. Яке число лежить на чотирьох одиницях ліворуч від 6 на числовому рядку?
10. Яке число лежить на двох одиницях ліворуч від 0 на числовому рядку?
11. Яке число лежить на двох одиницях праворуч від −5 на числовому рядку?
12. Яке число лежить на трьох одиницях праворуч від −6 на числовому рядку?
У вправах 13-24 для кожного з наступних наборів цілих чисел виконайте наступні завдання:
- Покладіть кожне з цілих чисел на числовому рядку.
- Перерахуйте числа по порядку, від найменшого до найбільшого.
13. 6, 1, −3 та −5
14. 5, −3, −5 та 2
15. 5, −6, 0 та 2
16. 4, 2, 6 і −4
17. −3, −5, 3 і 5
18. −4, 5, 2 та −6
19. −5, 4, 2 та −3
20. 6, 1, −3 та −1
21. 3, 5, −5 та −1
22. −4, 6, −2 та 3
23. −2, −4, 3 та −6
24. 2, −6, −4 та 5
У Вправи 25-36 в кожному з наступних вправ введіть символ нерівності < or the symbol > в поле для того, щоб отримана нерівність була істинним твердженням.
25. \( -4 \square 0\)
26. \(-4 \square 3\)
27. \(-2 \square -1\)
28. \(3 \square 0\)
29. \(-3 \square -1\)
30. \(6 \square 5\)
31. \(3 \square 6\)
32. \(-4 \square -2\)
33. \(-3 \square -6\)
34. \(0 \square -3\)
35. \(-1 \square 4\)
36. \(1 \square -4\)
У Вправи 37-52 спростіть кожне з наступних виразів.
37. − (−4).
38. − (−6).
39. |7|.
40. |1|.
41. |5|.
42. |3|.
43. −| − 11|.
44. −| − 1|.
45. | − 5|.
46. | − 1|.
47. −| − 20|.
48. −| − 8|.
49. | − 4|.
50. | − 3|.
51. − (−2).
52. − (−17).
У Вправи 53-64 для кожної з наступних вправ надайте ескіз числового рядка з вашою відповіддю.
53. Знайти два цілих числа на числовому рядку, що знаходяться на відстані 2 одиниці від цілого числа 2.
54. Знайти два цілих числа у числовому рядку, що знаходяться на відстані 2 одиниці від цілого числа −3.
55. Знайти два цілих числа у числовому рядку, що знаходяться на відстані 4 одиниці від цілого числа −3.
56. Знайти два цілих числа у числовому рядку, що знаходяться на відстані 2 одиниці від цілого числа −2.
57. Знайти два цілих числа у числовому рядку, що знаходяться на відстані 3 одиниці від цілого числа −2.
58. Знайти два цілих числа на числовому рядку, що знаходяться на відстані 4 одиниці від цілого числа 1.
59. Знайти два цілих числа на числовому рядку, що знаходяться на відстані 2 одиниці від цілого числа 3.
60. Знайти два цілих числа на числовому рядку, що знаходяться на відстані 3 одиниць від цілого числа 3.
61. Знайдіть у числовому рядку два цілих числа, що знаходяться на відстані 3 одиниці від цілого числа 0.
62. Знайти два цілих числа на числовому рядку, що знаходяться на відстані 4 одиниці від цілого числа 2.
63. Знайдіть у числовому рядку два цілих числа, що знаходяться на відстані 2 одиниці від цілого числа 0.
64. Знайти два цілих числа на числовому рядку, що знаходяться на відстані 3 одиниці від цілого числа 1.
65. Гребля. Найнижча точка піднесення штату Юта становить 2350 футів над рівнем моря і відбувається в Бівер-Дам Wash. Висловіть висоту цілим числом 66. Підводний планер. Підводний планер Національної океанічної та атмосферної адміністрації відбирає дно Атлантичного океану на 660 футів нижче рівня моря. Висловіть цю глибину як ціле число. Асоційований прес Час-Стандарт 4/19/09 67. Прибутки і збитки за перші шість місяців фінансового року для малого бізнесу показані на наступній гістограмі.
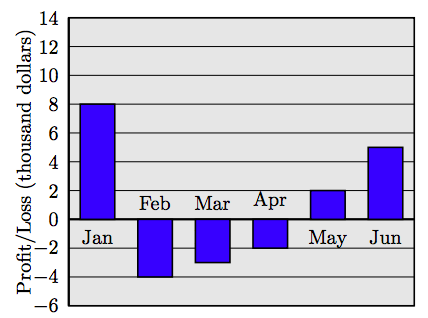
Створіть таблицю із зазначенням прибутку і збитку за кожен місяць. Використовуйте натуральні числа для прибутку та від'ємні цілі числа для збитку. Створіть лінійний графік, використовуючи дані у вашій таблиці 68. Прибутки і збитки за перші шість місяців фінансового року для малого бізнесу показані на наступній гістограмі.
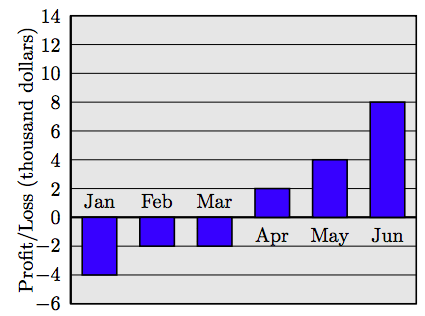
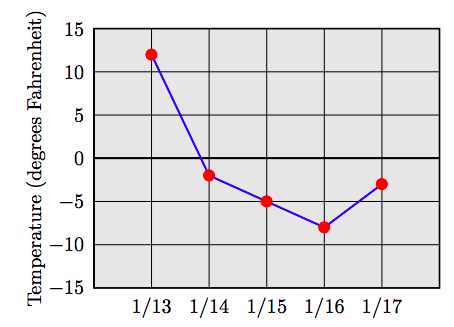
Створіть таблицю із зазначенням прибутку і збитку за кожен місяць. Використовуйте натуральні числа для прибутку та від'ємні цілі числа для збитку. Створіть лінійний графік, використовуючи дані у вашій таблиці 69. Наступний лінійний графік відображає записи низької температури (градуси за Фаренгейтом) протягом п'яти днів поспіль у Біг-Беар, Каліфорнія. Яке було найнижче показання температури за тиждень і на яку дату це відбулося?
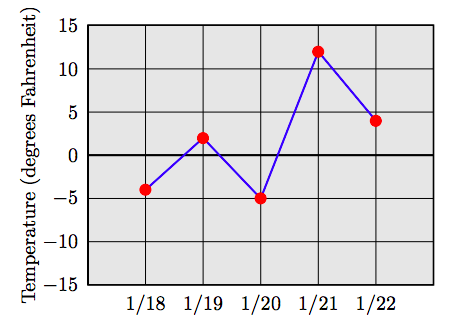
70. Наступний графік відображає записи низької температури (градуси за Фаренгейтом) протягом п'яти днів поспіль в Огдені, штат Юта. Яке було найнижче показання температури за тиждень і на яку дату це відбулося?
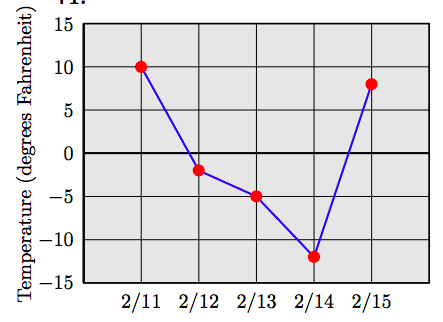
71. Наступна таблиця містить записи низької температури (градуси за Фаренгейтом) протягом п'яти днів поспіль у Літлтауні, штат Огайо. Створіть лінійний графік для даних.
| Дата | 11 лют | лют 12 | лют 13 | 14 лют | 15 лют |
| Низька температура | 10 | -2 | -5 | -12 | 8 |
72. Наступна таблиця містить записи низької температури (градуси за Фаренгейтом) протягом п'яти днів поспіль у MyTown, Оттава. Створіть лінійний графік для даних.
| Дата | 20 квіт | Кві 21 | Кві 22 | Кві 23 | Квіт 24 |
| Низька температура | -10 | -2 | 8 | 5 | -5 |
Відповіді
1.
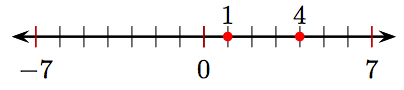
3.
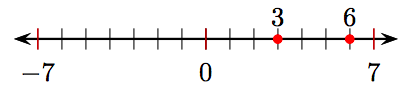
5.
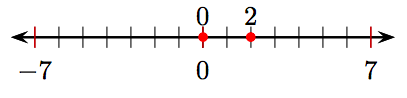
7.
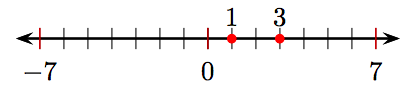
9.
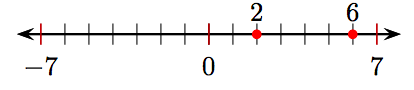
11.
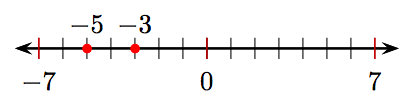
13.
i) Впорядкувати цілі числа 6, 1, −3 та −5 у числовому рядку.
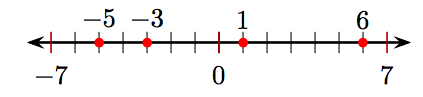
ii) −5, −3, 1, 6
15.
i) Впорядкувати цілі числа 5, −6, 0 та 2 у числовому рядку.
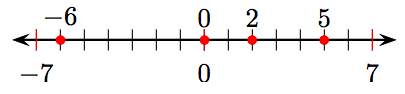
ii) −6, 0, 2, 5
17.
i) Впорядкувати цілі числа −3, −5, 3 та 5 у числовому рядку.
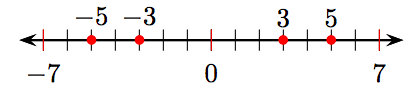
ii) −5, −3, 3, 5
19.
i) Впорядкувати цілі числа −5, 4, 2 та −3 у числовому рядку.
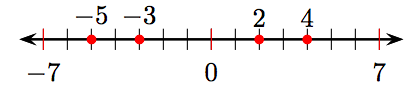
ii) −5, −3, 2, 4
21.
i) Впорядкувати цілі числа 3, 5, −5 та −1 у числовому рядку.
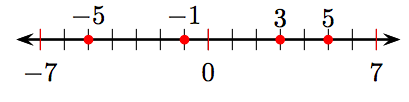
ii) −5, −1, 3, 5
23.
i) Впорядкувати цілі числа −2, −4, 3 та −6 у числовому рядку.
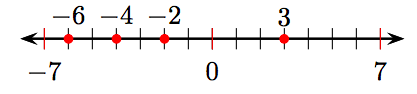
ii) −6, −4, −2, 3
25. −4 <0
27. −2 < −1
29. −3 < −1
31. 3 < 6
33. −3> −6
35. −1 < 4
37. 4
39. 7
41. 5
43. −11
45. 5
47. −20
49. 4
51. 2
53. 0 і 4.
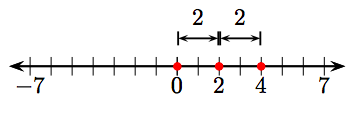
55. −7 і 1.
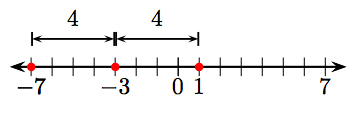
57. −5 і 1.
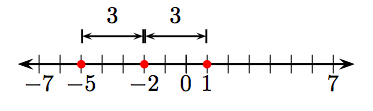
59. 1 і 5.
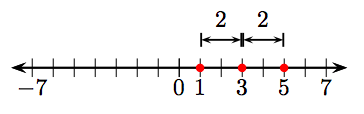
61. −3 і 3.
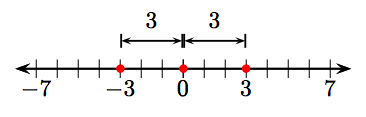
63. −2 і 2.
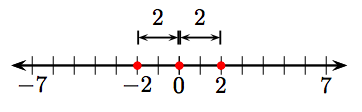
65. 2350 футів
67.
| Місяць | Прибуток/збиток |
| Січ | 8 |
| лют. | −4 |
| бер. | −3 |
| Квітень | −2 |
| Травень | 2 |
| черв. | 5 |
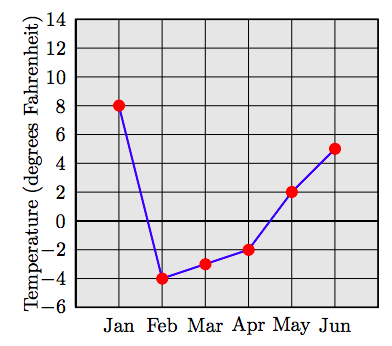
69. Приблизно −8 ◦ за Фаренгейтом 16 січня.
71.