7.5: Окружність кола
- Page ID
- 58946
Окружність кола - це периметр кола, довжина лінії, отриманої шляхом вирізання кола і «випрямлення кривих» (рис.\(\PageIndex{1}\)).
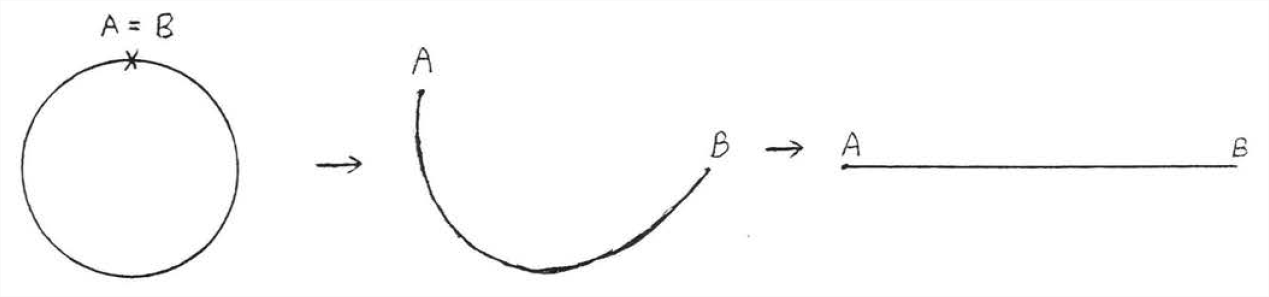
Безпосередньо вимірювати окружність більшості кругових предметів недоцільно. Кругову рулетку було б важко утримувати на місці, і вона буде спотворена, оскільки вона буде зігнута. Сам об'єкт був би зруйнований, якби ми спробували його розрізати і випрямити для вимірювання. На щастя, ми можемо обчислити окружність кола за його радіусом або діаметром, які легко виміряти.
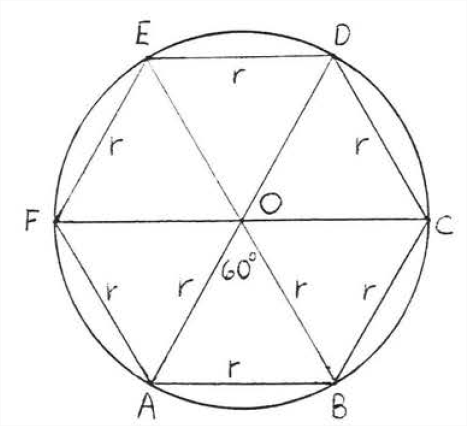
Приблизне значення для окружності окружності радіуса\(x\) можна отримати, обчисливши периметр правильного шестикутника радіуса,\(r\) вписаного в коло (рис.\(\PageIndex{2}\)). Бачимо, що окружність трохи більше периметра шестикутника, що в 6 разів перевищує радіус бика в 3 рази більше діаметра. Щоб отримати краще наближення, збільшуємо кількість сторін вписаного правильного багатокутника. Зі збільшенням кількості сторін правильного багатокутника багатокутник все більше схожий на коло (рис.\(\PageIndex{3}\)). У розділі 7.1 ми розрахували периметр 90-гранного правильного багатокутника в 3,141 рази більше діаметра або 6,282 рази більше радіуса. Периметр 1000-гранного правильного багатокутника виявився лише трохи більше, в 3,1416 разів більше діаметра або 6,283 рази більше радіуса. Тому здається розумним зробити висновок, що окружність кола приблизно в 3,14 рази більше діаметра або 6,28 рази більше радіуса.
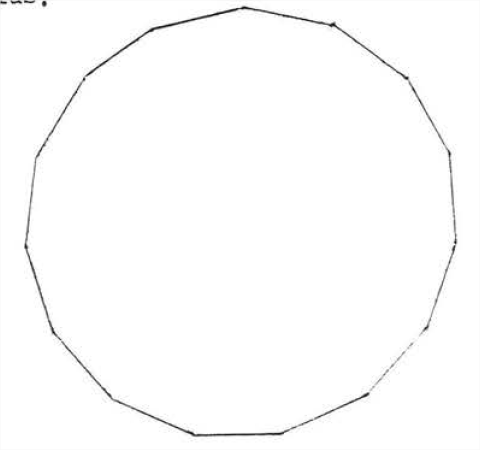
Окружність кола в\(\pi\) рази її діаметр або в\(2 \pi\) рази його радіус, де\(\pi\) приблизно 3,14.
\[C=\pi d\]
або
\[C =2 \pi r\]
Символ\(\pi\) (грецька буква пі) - стандартне позначення числа, на яке необхідно помножити діаметр кола, щоб отримати окружність. Його значення зазвичай приймається 3,14, хоча 3.1416 і\(\dfrac{22}{7}\) є іншими часто використовуваними наближеннями. Ці числа не є точними, для подібного\(\sqrt{2}\), можна показати, що\(\pi\) це ірраціональне число (нескінченне неповторюване десяткове число). Його значення до 50 знаків після коми дорівнює
3. 14159 26535 89793 23846 26433 83279 50288 41971 69399 37511
Знайдіть окружність:
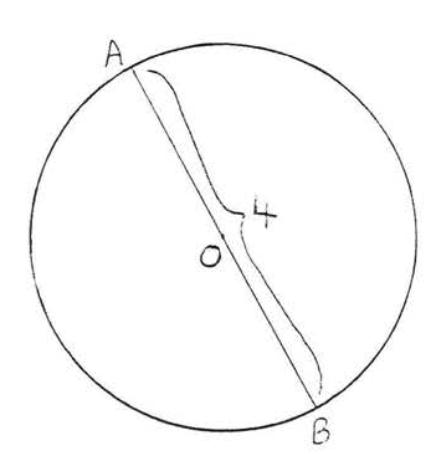
Рішення
\(C = \pi d = (3.14)(4) = 12.56\).
Відповідь: 12.56
Довжину дуги визначаємо таким же чином, як ми визначили окружність. Розраховуємо його шляхом множення окружності на відповідний дріб.
Знайдіть довжину дуги\(\widehat{AB}\):
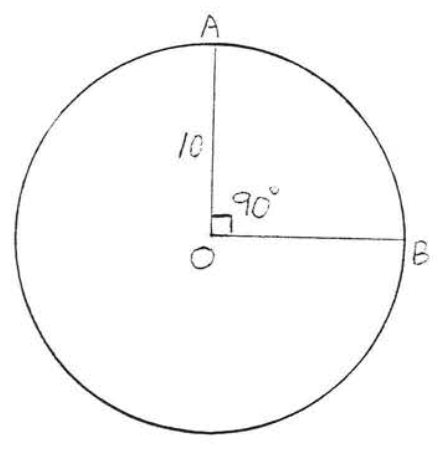
Рішення
\(C = 2\pi r = 3(3.14)(10) = 62.8\). Так як\(90^{\circ}\)\(\dfrac{1}{4}\) є\(360^{\circ}\),\(\widehat{AB}\) є\(\dfrac{1}{4}\) окружності\(C\). \(\widehat{AB} = \dfrac{1}{4} C = \dfrac{1}{4} (62.8) = 15.7\).
Відповідь: 15.7.
Як ми вже зазначали в розділі 7.4, символ plain = буде використовуватися для довжини дуги, а\(\stackrel{\circ}{=}\) символ буде використовуватися для градусів. Таким чином, в\(PageIndex{2}\) прикладі,\(\widehat{AB} = 15.7\) але\(\widehat{AB} \stackrel{\circ}{=} 90^{\circ}\).
Ми також можемо використовувати наступну формулу, щоб знайти довжину дуги:
\[\text{Arc Length} = \dfrac{\text{Degrees in Arc}}{360^{\circ}} \cdot \text{Circumference}\]
або просто
\[L = \dfrac{D}{360} \cdot C\]
Таким чином, у\(\PageIndex{2}\) прикладі,
\(L = \dfrac{D}{360} \cdot C = \dfrac{90}{360} (62.8) = \dfrac{1}{4} (62.8) = 15.7\)
Знайдіть довжину дуги\(\widehat{AB}\):
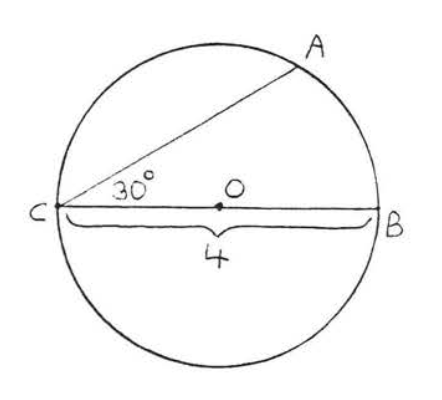
Рішення
\(C = \pi d =(3.14)(4) = 12.56\). \(\angle ACB \stackrel{\circ}{=} \dfrac{1}{2} \widehat{AB} \stackrel{\circ}{=} 30^{\circ}\). Тому\(\widehat{AB} \stackrel{\circ}{=} 60^{\circ}\). Використовуючи формулу довжини дуги,
\(L = \dfrac{D}{360} C = \dfrac{60}{360} (12.56) = \dfrac{1}{6} (12.56) = 2.09\).
Відповідь: 2.09.
Знайдіть діаметр кола, окружність якого дорівнює 628.
Рішення
Впускаючи\(C = 628\) і\(\pi = 3.14\) в формулу для окружності, ми маємо
\[\begin{array} {rcl} {c} & = & {\pi d} \\ {628} & = & {(3.14) d} \\ {\dfrac{628}{3.14}} & = & {\dfrac{3.14d}{3.14}} \\ {200} & = & {d} \end{array}\]
Відповідь: діаметр = 200.
Одометр і спідометр автомобіля калібруються відповідно до кількості обертань одного з коліс. Припустимо, діаметр шини, встановленої на колесі, становить 2 фути. Тоді його окружність -\(C = \pi d = (3.14)(2) = 6.28\) стопи. Оскільки 1 миля = 5280 футів, колесо буде обертатися\(5280 \div 6.28 = 841\) раз кожну милю. Якщо розмір шин змінений з яких-небудь причин, одометр і спідометр повинні бути перекалібровані.
Окружність землі спочатку точно розрахував грецький географ Ератосфен (бл. 284 - 192 до н.е.), який жив в Олександрії, Єгипет. Було відомо, що опівдні в день літнього сонцестояння сонячні промені повністю освітлювали колодязі Сієни (нині називають Асуан), Єгипту. Це вказувало на те, що промені сонця були перпендикулярні поверхні Землі в Сієні, і так, на малюнку\(\PageIndex{4}\),\(\overleftrightarrow{DS}\) проходить через земний центр\(O\). При цьому в Олександрії Ератосфен спостерігав, що сонячні промені робили кут\(\angle BAC = 7.2^{\circ}\) в\(360^{\circ}\) (тобто\(7.2^{\circ}\)) з перпендикуляром (на рис.\(\PageIndex{4}\)).\(\dfrac{1}{50}\) Промені сонця приймаються паралельними звідси\(\angle AOS = \angle BAC = 7.2^{\circ}\) і\(\widehat{AS} \stackrel{\circ}{=} 7.2^{\circ}\). Так як відстань між Олександрією і Сієною становить близько 500 миль (довжина\(\widehat{AS}\)). Ератосфен зміг придумати надзвичайно точну цифру близько (50) (500) = 25 000 миль для окружності землі.
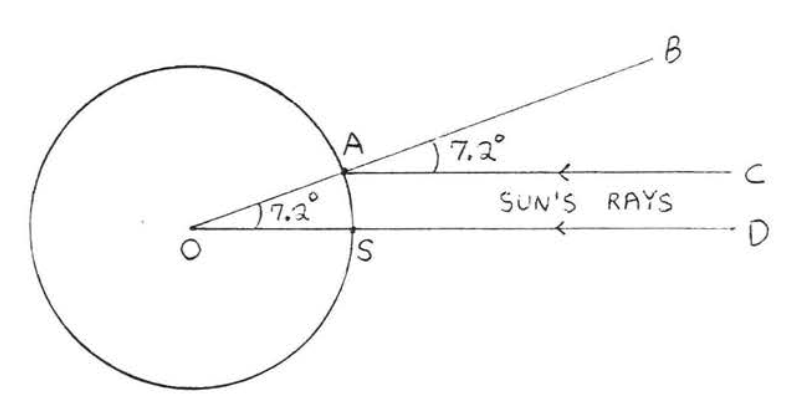
Малюнок\(\PageIndex{4}\). Сонячні промені були перпендикулярні поверхні Землі в\(S\) той же час, коли вони робили кут\(7.2^{\circ}\) з перпендикуляром в\(A\).
Ранні сирі оцінки вартості\(\pi\) були зроблені китайцями (\(\pi = 3\)), вавилонянами (\(\pi = 3\)або\(3\dfrac{1}{8}\)) та єгиптянами (\(\pi = 3.16\)). Значення також\(\pi = 3\) є тим, що передбачається в Біблії (I Царів 7:23). Перший точний розрахунок проводив Архімед (287 - 212 до н.е.), найбільший математик давнини, (Архімед також був відомим фізиком і винахідником. Наприклад, він відкрив принцип, що тверде тіло, занурене в рідину, підживлюється силою, рівною вазі витісненої рідини.) У своєму трактаті «Про вимір окружності» він наближає окружність, обчислюючи периметри вписаних і обмежених правильних багатокутників (рис.\(\PageIndex{5}\)). Це схоже на метод, який ми описали в тексті, за винятком того, що Архімед не мав точних тригонометричних таблиць і повинен був вивести свої власні формули, Проводячи процес до випадку багатокутника з 96 сторін він знайшов значення бути між\(3\dfrac{10}{71}\) і\(3 \dfrac{1}{7}\). (До речі, Архімед насправді не використовував символ\(\pi\). Символ не\(\pi\) використовувався для відношення окружності до діаметра кола до 18 ст.)
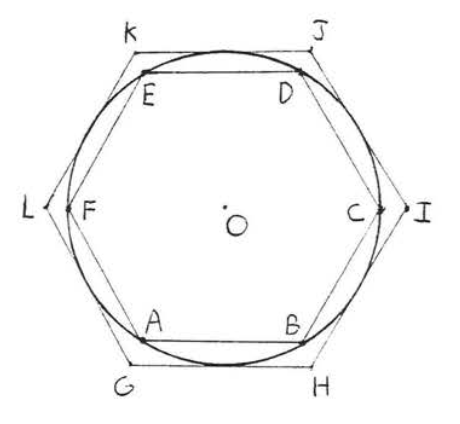
Процедура Архімеда була початком довгих історій; все більш точних розрахунків вартості\(\pi\). Починаючи з 17 століття ці розрахунки передбачали використання нескінченних рядів, таких як
\[\dfrac{1}{4}\pi = 1 - \dfrac{1}{3} + \dfrac{1}{5} - \dfrac{1}{7} + \dfrac{1}{9} - ...\]
виведення яких CA.TL можна знайти в багатьох підручниках з числення. Зовсім недавно за допомогою комп'ютера було визначено значення\(\pi\) до мільйона знаків після коми.
ПРОБЛЕМИ
Для кожного з наступних використовують\(\pi = 3.14\).
1 - 8. Знайдіть окружність кожного кола:
1.
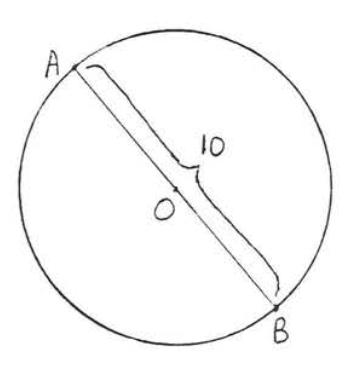
2.
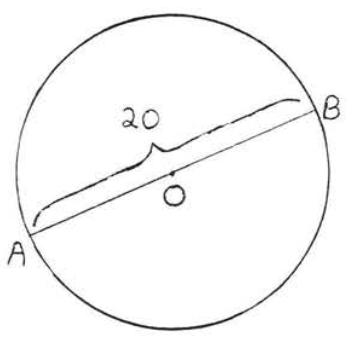
3.
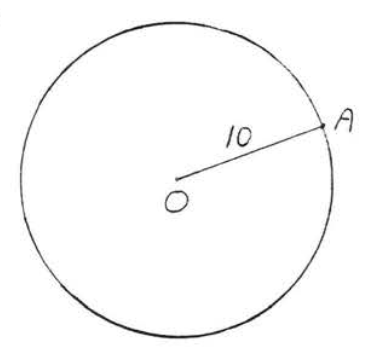
4.
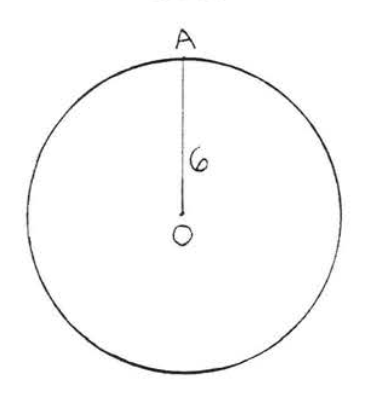
5.
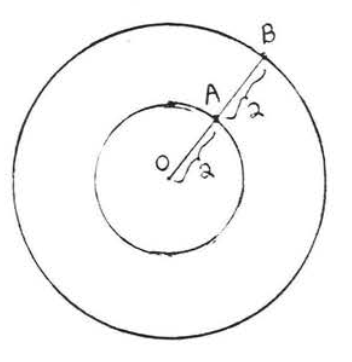
6.
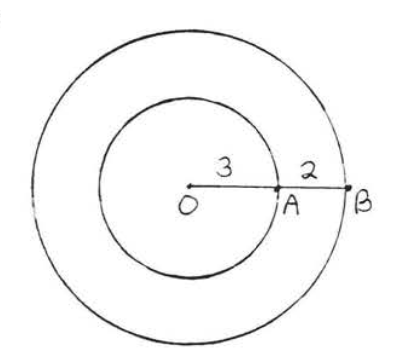
7.
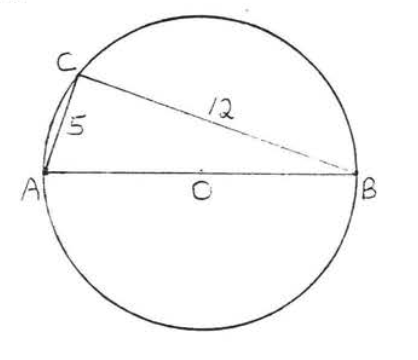
8.
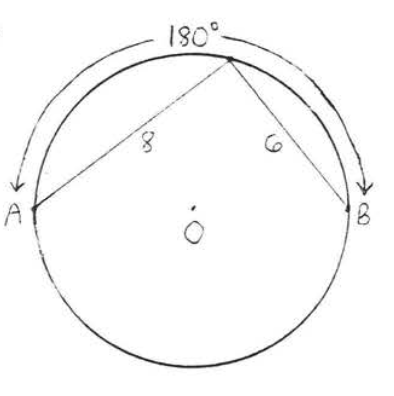
9 - 14. Знайдіть довжину дуги\(\widehat{AB}\):
9.
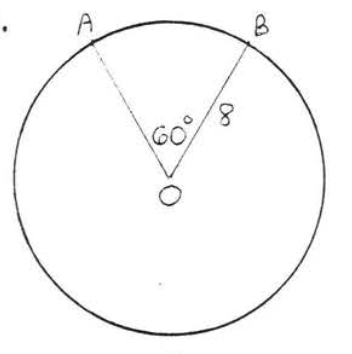
10.
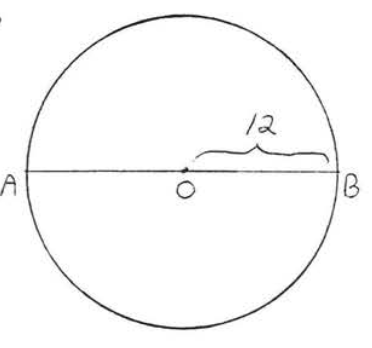
11.
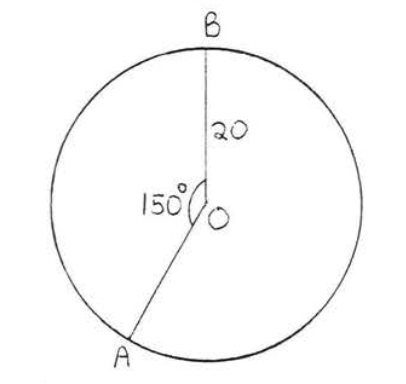
12.
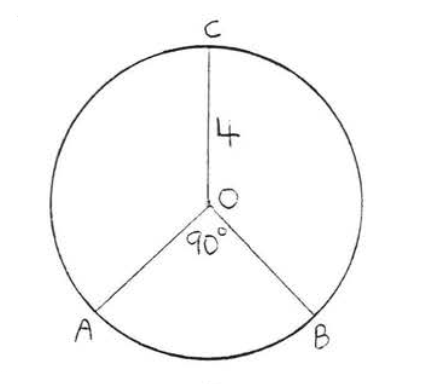
13.
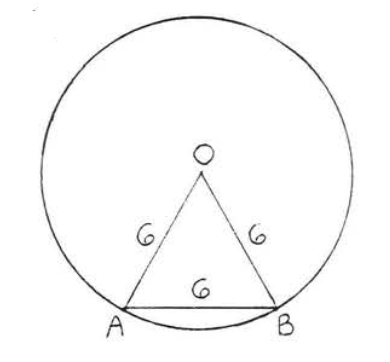
14.
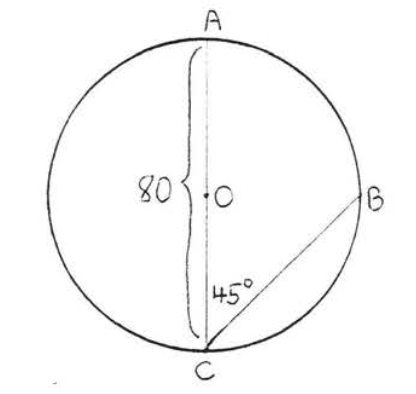
15 - 16. Знайдіть довжини дуг\(\widehat{AB}\) і\(\widehat{CD}\):
15.
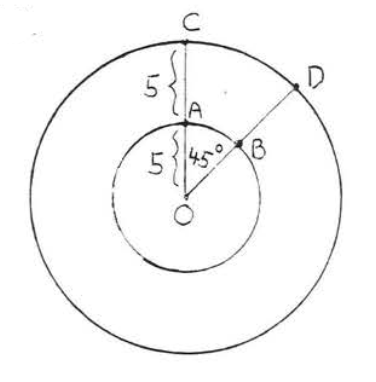
16.
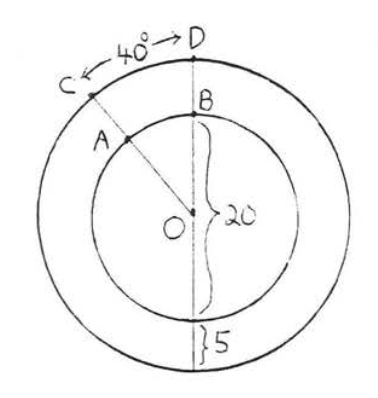
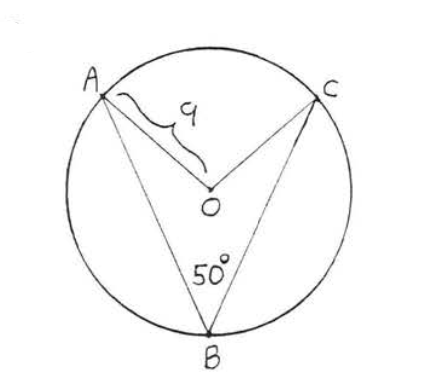
17 - 18. Знайдіть довжину великої дуги\(\widehat{ABC}\):
17.
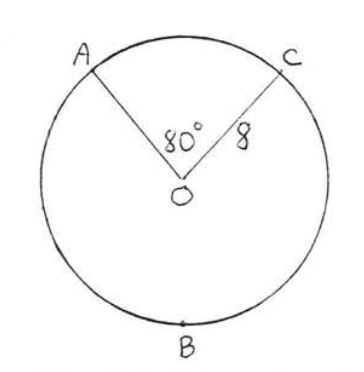
18.
19 - 22. Знайдіть окружність кола, який...
19. діаметр 30.
20. діаметр дорівнює 8.
21. радіус дії 10.
22. радіус дії дорівнює 6.
23. Знайдіть радіус і діаметр кола, окружність якого дорівнює 314.
24. Знайдіть радіус і діаметр кола, окружність якого дорівнює 100 (залиште відповідь на найближче ціле число).
25. Яка окружність автомобільного колеса, діаметр якого становить 14 дюймів?
26. Яка окружність 12-дюймового запису фонографа?
27. Який діаметр землі, якщо її окружність становить 24 830 миль?
28. Який діаметр чверті милі кругової бігової доріжки?
