7.6: Площа кола

У главі VI ми визначили площу замкнутої фігури як кількість квадратних одиниць, що містяться в малюнку. Щоб застосувати це визначення до кола, ми знову припустимо, що коло - це правильний багатокутник з великою кількістю сторін. Потім виходить наступна формула:

Теорема$\PageIndex{1}$

Площа кола в$\pi$ рази перевищує квадрат його радіуса.

$$A = \pi r^2$$

Доказ

Площа кола з радіусом приблизно$r$ дорівнює площі правильного багатокутника з апофемом,$a =r$ описаним навколо кола (рис.$\PageIndex{1}$). Наближення стає більш точним, оскільки кількість сторін багатокутника стає більшою. При цьому периметр багатокутника наближається до окружності кола (=$2\pi r$).

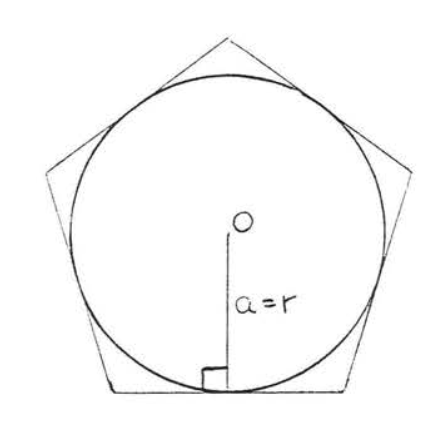
Малюнок$\PageIndex{1}$: Правильний багатокутник з$a = r$ апофемом, описаним навколо кола з радіусом$r$.

Приклад$\PageIndex{1}$

Знайдіть площу кола:

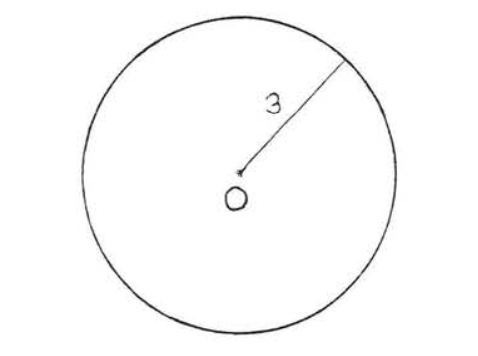
Рішення

$A = \pi r^2 = \pi (3)^2 = 9\pi = 9(3.14) = 28.26$

Відповідь: 28.26

Використовуючи формулу для площі правильного багатокутника (Теорема 7.1.4, розділ 7.1) ми маємо

$$\text{area of circle} = \text{area of polygon} = \dfrac{1}{2}aP = \dfrac{1}{2} r(2\pi r) = \pi r^2.$$

Приклад$\PageIndex{2}$

Знайдіть затінену область:

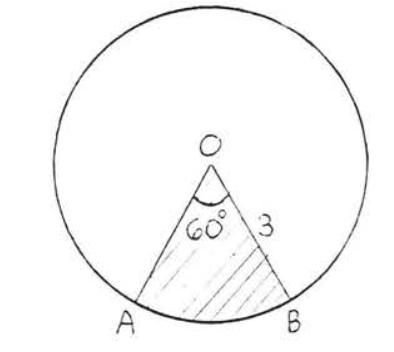
Рішення

Малюнок$\PageIndex{2}$: Коло, розділене на шість рівних частин.

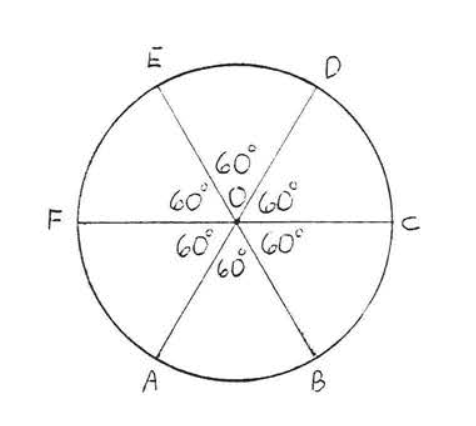
Затінена область$OAB$ становить загальну$\dfrac{60}{360} = \dfrac{1}{6}$ площу (див. Рис.$\PageIndex{2}$). Площа всього кола =$\pi r^2 = \pi (3)^2 = 9\pi = 9(3.14) = 28.26$. Тому площа м$OAB = \dfrac{1}{6} (28.26) = 4.71$.

Відповідь: 4.71

Затінена область в Прикладі$\PageIndex{2}$ називається сектором кола. Приклад$\PageIndex{2}$ пропонує наступну формулу для площі сектора:

$$\text{Area of sector} = \dfrac{\text{Degrees in arc of sector}}{360} \cdot \text{Area of circle}$$

або просто

$$A = \dfrac{D}{360} \pi r^2$$

Використовуючи цю формулу, рішення Приклад$\PageIndex{2}$ буде

$$A = \dfrac{D}{360} \pi r^2 = \dfrac{60}{360} (3.14)(3)^2 = \dfrac{1}{6} (3.14)(9) = \dfrac{1}{6} (28.26) = 4.71$$

Приклад$\PageIndex{3}$

Знайдіть затінену область:

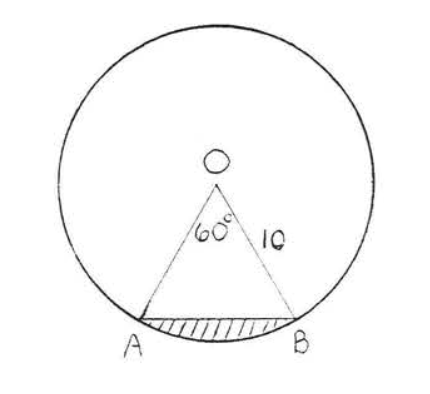
Рішення

Давайте спочатку знайдемо площу трикутника$OAB$ (рис.$\PageIndex{3}$).

Малюнок$\PageIndex{3}$: Трикутник$OAB$ з основою$b$ і висотою$h$.

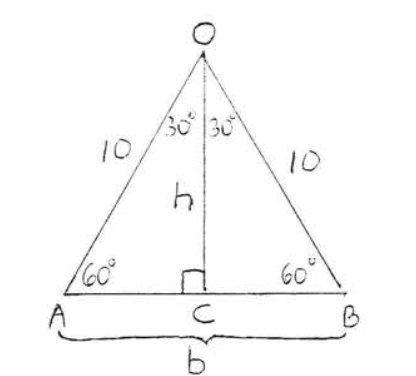
$\triangle OAB$рівносторонній з підставою$b = AB = 10$. Малюнок по висоті у$h = OC$ нас$\triangle AOC$ є, що$30^{\circ} - 60^{\circ} -90^{\circ}$ трикутник з$AC = 5$ і$h = 5\sqrt{3}$. Тому площа м$\triangle OAB = \dfrac{1}{2} bh = \dfrac{1}{2} (10) (5\sqrt{3}) = 25 \sqrt{3}$. Тому

$$\begin{array} {rcl} {\text{shaded area}} & = & {\text{area of sector } OAB - \text{area of triangle } OAB} \\ {} & = & {\dfrac{D}{360} \pi r^2 - \dfrac{1}{2} bh} \\ {} & = & {\dfrac{60}{360} \pi (10)^2 - \dfrac{1}{2} (10) (5\sqrt{3})} \\ {} & = & {\dfrac{1}{6} (100\pi) - \dfrac{1}{2} (50\sqrt{3})} \\ {} & = & {\dfrac{50\pi}{3} - 25\sqrt{3}} \\ {} & = & {\dfrac{50(3.14)}{3} - 25(1.732)} \\ {} & = & {52.33 - 43.30 = 9.03} \end{array}$$

Відповідь:$\dfrac{50\pi}{3} - 25\sqrt{3}$ або 9.03.

Затінена область в Прикладі$\PageIndex{3}$ називається сегментом кола. Площа відрізка отримують шляхом віднімання площі трикутника з площі сектора.

Приклад$\PageIndex{4}$

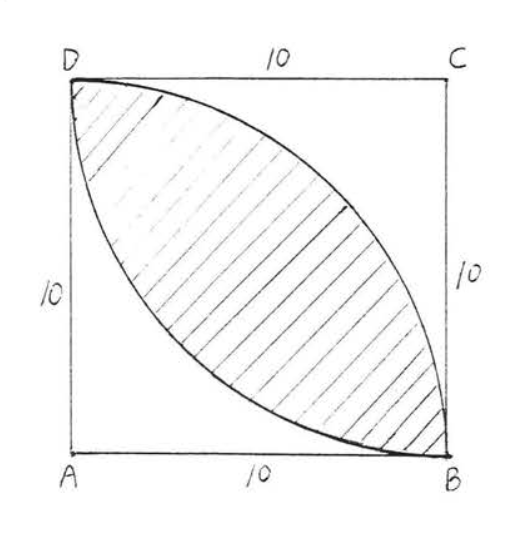
Знайдіть затінену область:

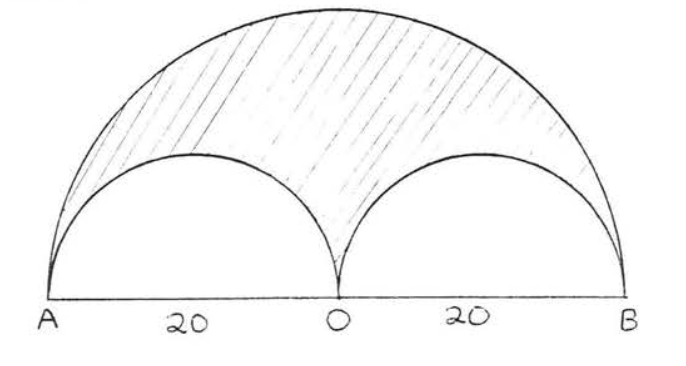
Рішення

Площа великого півкола =$\dfrac{1}{2} \pi r^2 = \dfrac{1}{2} \pi (20)^2 = \dfrac{1}{2} (400) \pi = 200 \pi$. Площа кожного з менших півкіл =$\dfrac{1}{2} \pi r^2 = \dfrac{1}{2} \pi (10)^2 = \dfrac{1}{2} (100) \pi = 50\pi$. Тому

$$\begin{array} {rcl} {\text{shaded area}} & = & {\text{area of large semicircle - (2)(area of small semicircles)}} \\ {} & = & {200 \pi - 2(50\pi)} \\ {} & = & {200\pi - 100\pi} \\ {} & = & {100 \pi = 100 (3.14) = 314} \end{array}$$

Відповідь:$100 \pi$ або 314.

Історична записка

Задача 50 Рхіндського папірусу, математичного трактату, написаного єгипетським писарем приблизно в 1650 році до н.е., стверджує, що площа кругового поля діаметром 9 одиниць така ж, як площа квадрата зі стороною 8 одиниць. Це еквівалентно$A = (\dfrac{8}{9} d)^2$ використанню формули для пошуку площі кола. Якщо ми дозволимо$d = 2r$ це стане$A = (\dfrac{8}{9} d)^2 = (\dfrac{8}{9} \cdot 2r)^2 = (\dfrac{16}{9} r)^2 = \dfrac{256}{81} r^2$ або приблизно$3.16 r^2$. Порівнюючи це з нашою сучасною формулою,$A = \pi r^2$ ми виявляємо, що стародавні єгиптяни мали надзвичайно гарне наближення, 3,16, для значення$\pi$.

У тій же роботі, в якій він обчислював значення$\pi$, Архімед дає формулу для площі кола (див. Історичну записку, розділ 7.5). Він стверджує, що площа кола дорівнює площі прямокутного трикутника, основа якого$b$ дорівнює довжині кола і висота якого$h$ дорівнює радіусу. Впустивши$b = C$ і$h = r$ в формулу для площі трикутника, отримаємо$A = \dfrac{1}{2} bh = \dfrac{1}{2} Cr = \dfrac{1}{2} (2\pi r) = \pi r^2$, сучасну формулу.

ПРОБЛЕМИ

1 - 6. Знайдіть площу кола (використовуйте$\pi = 3.14$):

1.

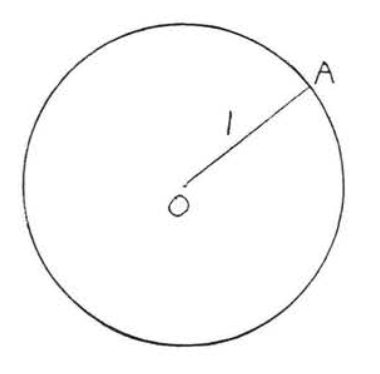
2.

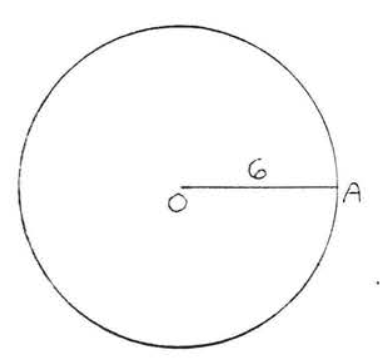
3.

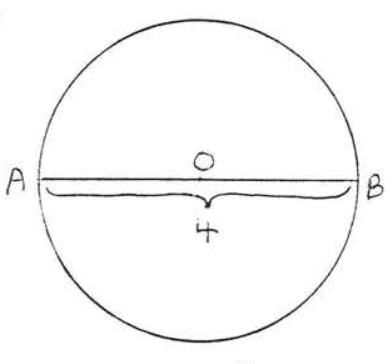
4.

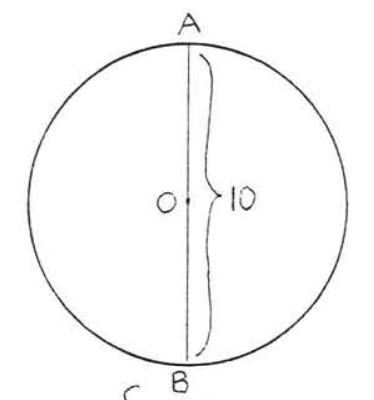
5.

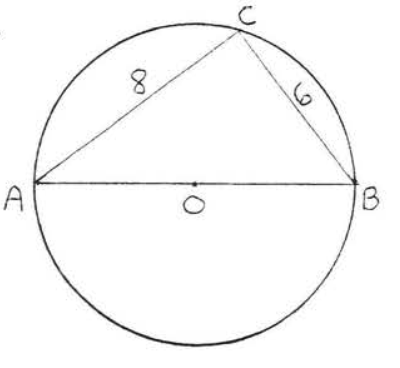
6.

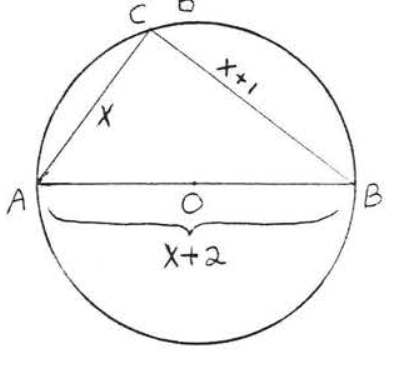
7 - 10. Знайдіть площу кола за допомогою... (використання$\pi = 3.14$)

7. радіус дії 20.

8. радіус дії 2.5.

9. діаметр 12.

10. діаметр 15.

11 - 14. Знайдіть затінену область (використовуйте$\pi = 3.14$):

11.

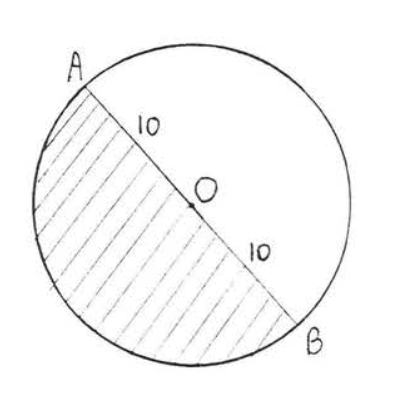
12.

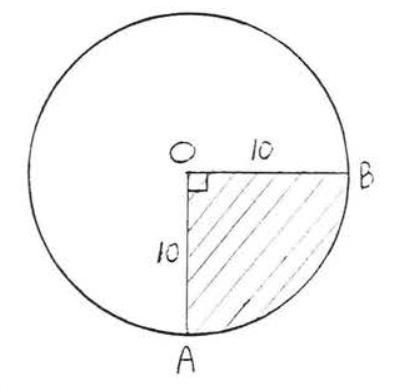
13.

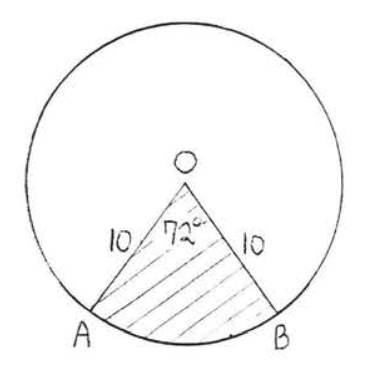
14.

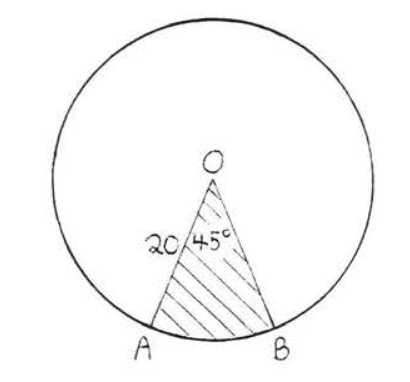
15 - 30. Знайдіть затінену область. Відповіді можуть бути залишені як в терміні,$\pi$ так і в радикальній формі.

15.

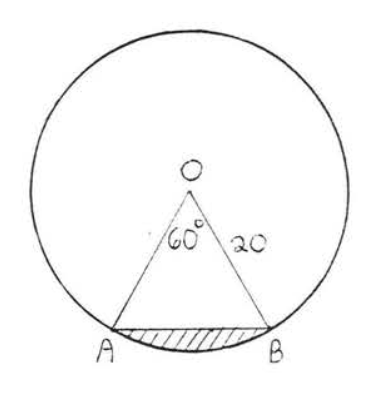
16.

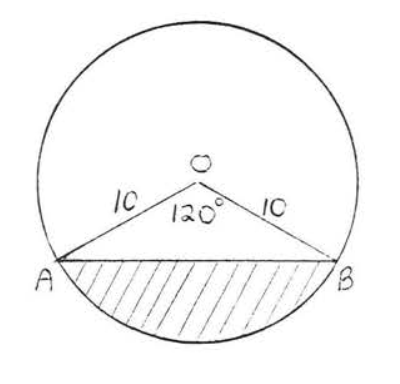
17.

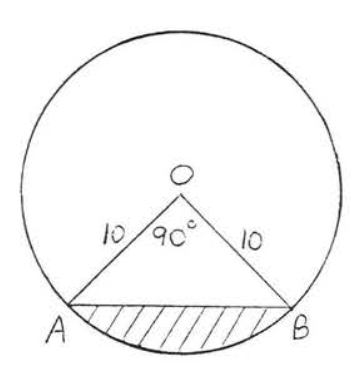
18.

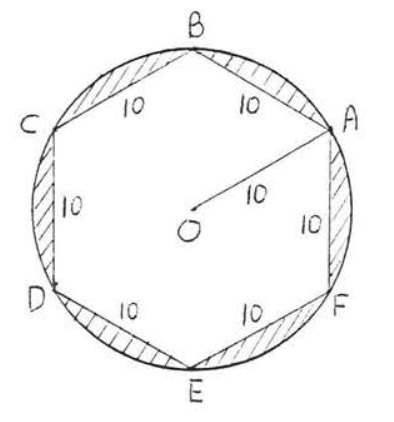
19.

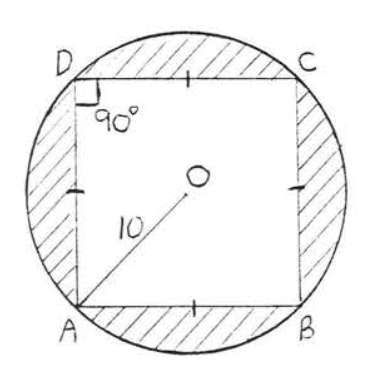
20.

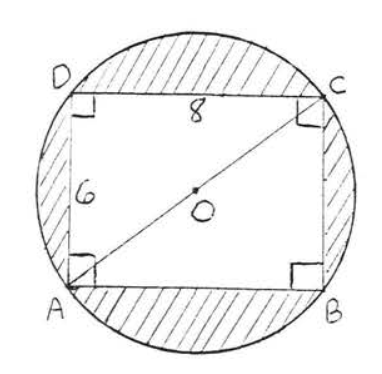
21.

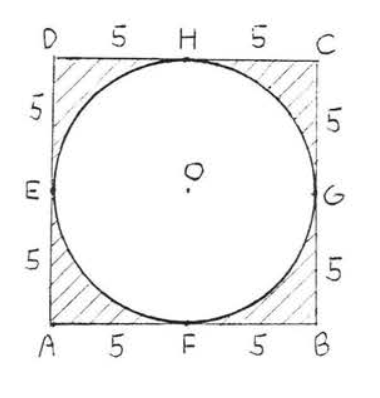
22.

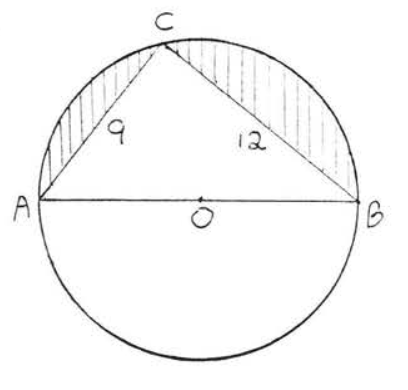
23.

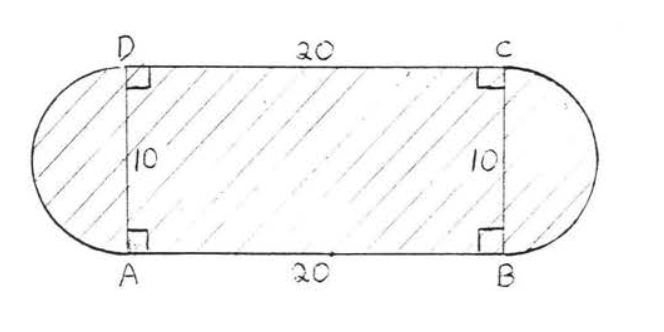
24.

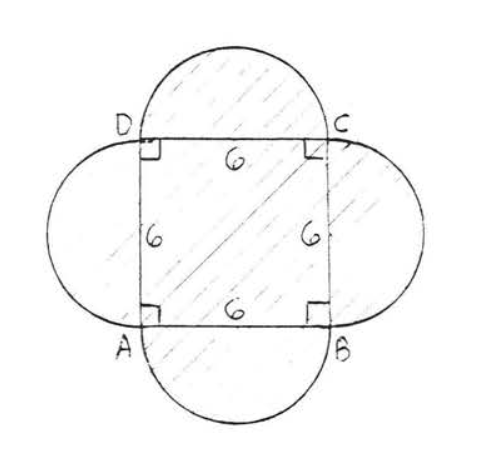
25.

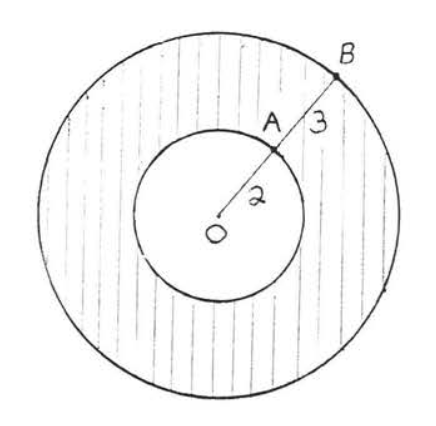
26.

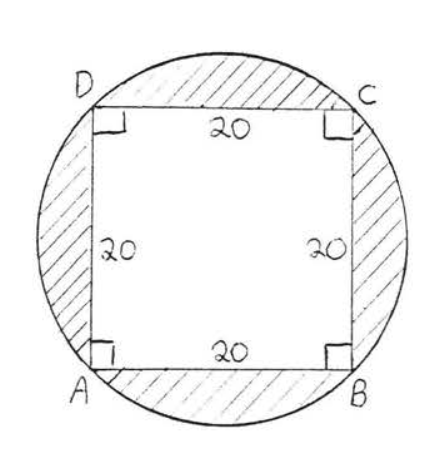
27.

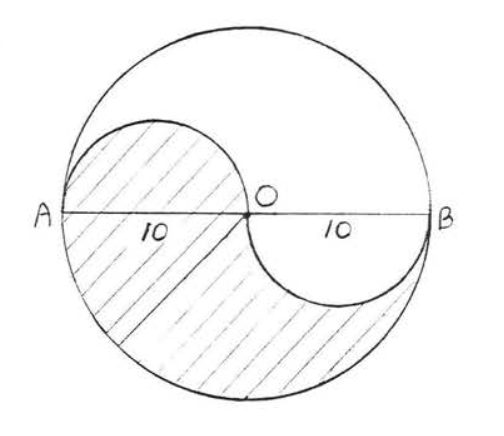
28.

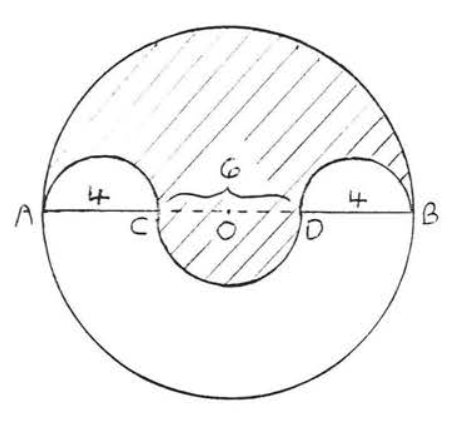
29.

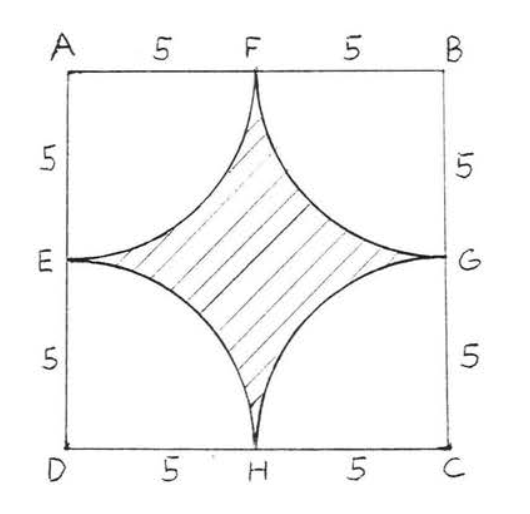
30.