13.1: Кути
- Page ID
- 61367
Цілі навчання
- Намалюйте кути в стандартному положенні.
- Перетворення між градусами і радіанами.
- Знайти котермінальні кути.
- Знайти довжину дуги окружності.
- Використовуйте лінійну та кутову швидкість для опису руху по круговому шляху.
Гольфіст гойдалки вдарити м'яч над піском пастку і на зелений. Пілот авіакомпанії маневрує літаком у напрямку вузької злітно-посадкової смуги. Дизайнер суконь створює останню моду. Що спільного у них всіх? Всі вони працюють з кутами, і так робимо всі ми в той чи інший час. Іноді нам потрібно виміряти кути точно за допомогою приладів. Інший раз ми оцінюємо їх або оцінюємо їх на око. У будь-якому випадку, правильний кут може зробити різницю між успіхом і невдачею в багатьох починаннях. У цьому розділі ми розглянемо властивості кутів.
Малювання кутів у стандартному положенні
Правильне визначення кута спочатку вимагає, щоб ми визначили промінь. Промінь складається з однієї точки на лінії і всіх точок, що йдуть в одному напрямку від цієї точки. Перша точка називається кінцевою точкою променя. Ми можемо посилатися на конкретний промінь, вказавши його кінцеву точку та будь-яку іншу точку на ньому. Промінь на малюнку\(\PageIndex{1}\) може бути названий як промінь EF, або у формі символу\(\overrightarrow{EF}\).
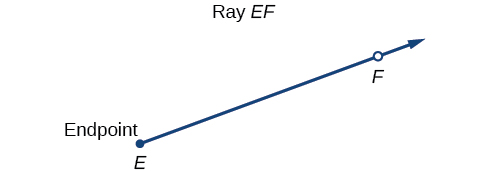
Кутом називається об'єднання двох променів, що мають загальну кінцеву точку. Кінцева точка називається вершиною кута, а два промені - сторони кута. Кут на малюнку\(\PageIndex{2}\) формується з\(\overrightarrow{ED}\) і\(\overrightarrow{EF}\). Кути можуть бути названі за допомогою точки на кожному промені і вершині, наприклад кут DEF, або у формі символу\(∠DEF.\)
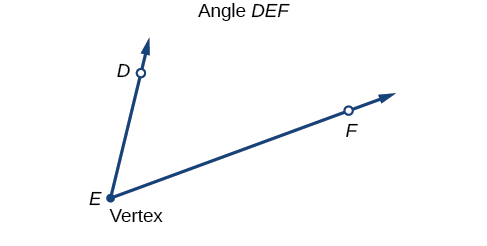
Грецькі літери часто використовуються як змінні для вимірювання кута. Таблиця\(\PageIndex{1}\) - це список грецьких букв, які зазвичай використовуються для представлення кутів, а зразок кута показаний на малюнку\(\PageIndex{3}\).
| \(θ\) | \(φ \text{ or }ϕ\) | \(α\) | \(β\) | \(γ\) |
| тета | Фі | альфа | бета-версія | гамма |
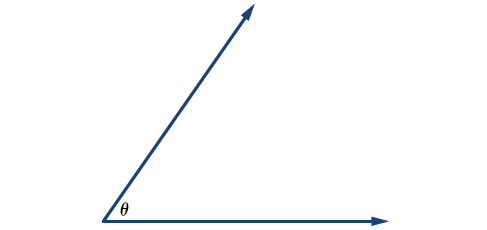
Малюнок \(\PageIndex{3}\): Кут тета, показаний як\(∠θ\)
Створення кута - це динамічний процес. Починаємо з двох променів, що лежать один на одному. Один залишаємо закріпленим на місці, а інший обертаємо. Фіксований промінь є початковою стороною, а повернутий промінь - кінцевою стороною. Для того, щоб визначити різні сторони, ми вказуємо обертання невеликою дугою і стрілкою близько до вершини, як на малюнку\(\PageIndex{4}\).
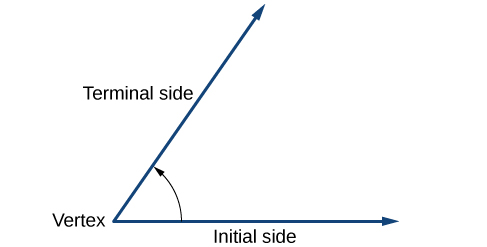
Як ми обговорювали на початку розділу, існує багато застосувань для кутів, але для того, щоб правильно їх використовувати, ми повинні вміти їх вимірювати. Міра кута - величина обертання від початкової сторони до кінцевої сторони. Напевно, найбільш звичною одиницею виміру кута є градус. Один градус має\(\frac{1}{360}\) кругове обертання, тому повне кругове обертання містить 360 градусів. Кут, виміряний у градусах, завжди повинен включати одиницю «градуси» після числа або включати символ градуса°. Наприклад, 90 градусів = 90°.
Щоб формалізувати нашу роботу, почнемо з малювання кутів на координатній площині x - y. Кути можуть зустрічатися в будь-якому положенні на координатній площині, але для порівняння угода полягає в тому, щоб проілюструвати їх у тому ж положенні, коли це можливо. Кут знаходиться в стандартному положенні, якщо його вершина розташована біля початку, а його початкова сторона простягається вздовж позитивної осі x. Див\(\PageIndex{5}\). Малюнок.
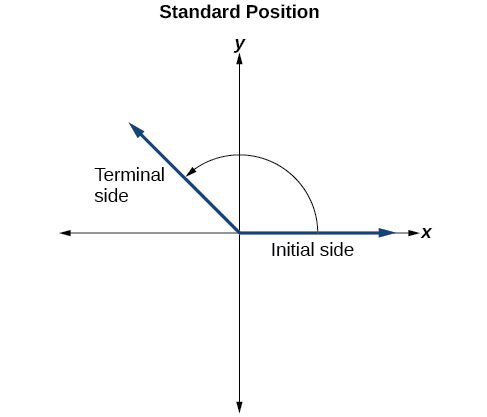
Якщо кут вимірюється в напрямку проти годинникової стрілки від початкової сторони до кінцевої сторони, кут вважається позитивним. Якщо кут вимірюється за годинниковою стрілкою, кут вважається негативним.
Нанесення кута в стандартному положенні завжди починається однаково - намалюйте початкову сторону вздовж позитивної осі x. Щоб розмістити кінцеву сторону кута, ми повинні обчислити частку повного повороту, який представляє кут. Ми робимо це, розділивши вимірювання кута в градусах на 360°. Наприклад, щоб намалювати кут 90°, ми обчислюємо це\(\frac{90°}{360°}=\frac{1}{4}\). Отже, кінцева сторона буде на одну четверту шляху по колу, рухаючись проти годинникової стрілки від позитивної осі х. Щоб намалювати кут 360°, ми обчислюємо це\(\frac{360°}{360°}=1\). Так кінцева сторона буде 1 повне обертання по колу, рухаючись проти годинникової стрілки від позитивної осі х. При цьому початкова сторона і сторона клеми перекриваються. Див\(\PageIndex{6}\). Малюнок.
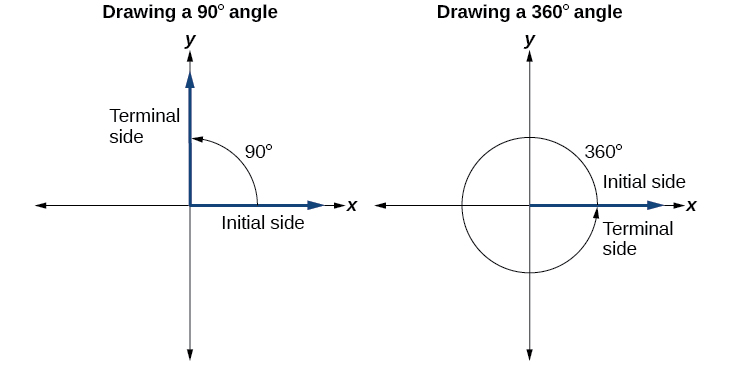
Оскільки ми визначаємо кут у стандартному положенні його початковою стороною, у нас є особливий тип кута, кінцева сторона якого лежить на осі, квадратний кут. Цей тип кута може мати міру 0°, 90°, 180°, 270° або 360°. Див\(\PageIndex{7}\). Малюнок.
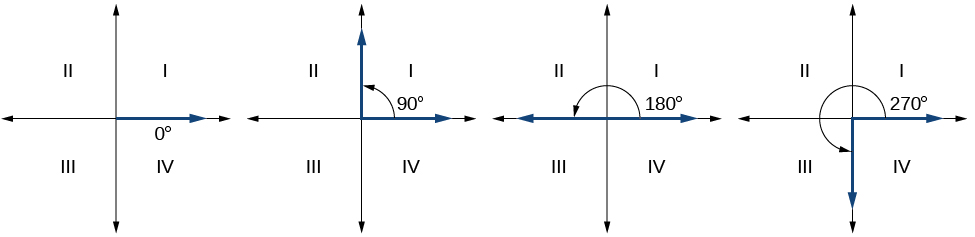
КВАДРАТНІ КУТИ
Квадратні кути - це кути в стандартному положенні, кінцева сторона яких лежить на осі, включаючи 0°, 90°, 180°, 270° або 360°.
З урахуванням вимірювання кута в градусах, намалюйте кут в стандартному положенні
- Висловіть вимір кута як частку 360°.
- Зменшіть дріб до найпростішої форми.
- Намалюйте кут, який містить ту саму частку кола, починаючи з позитивної осі x і рухаючись проти годинникової стрілки для позитивних кутів і за годинниковою стрілкою для негативних кутів.
Приклад\(\PageIndex{1}\): Drawing an Angle in Standard Position Measured in Degrees
- Намалюйте кут 30° у стандартному положенні.
- Намалюйте кут −135° у стандартному положенні.
Рішення
- Розділіть вимір кута на 360°.
\[\dfrac{30°}{360°}=\dfrac{1}{12}\]
Щоб переписати дріб у більш звичний дріб, ми можемо визнати, що
\[\dfrac{1}{12}=\dfrac{1}{3}(\frac{1}{4})\]
Одна дванадцята дорівнює третині чверті, тому, розділивши чверть обертання на третини, ми можемо намалювати лінію під 30°, як на малюнку\(\PageIndex{8}\).
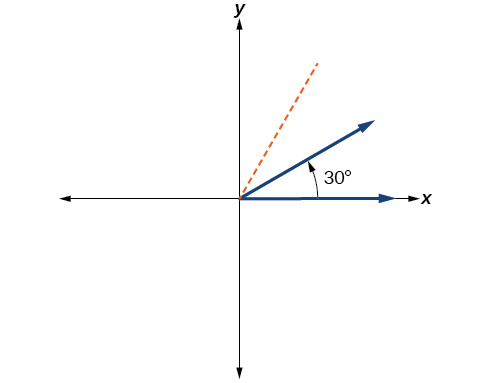
Малюнок\(\PageIndex{8}\) - Розділіть вимір кута на 360°.
\[\dfrac{−135°}{360°}=−\dfrac{3}{8}\]
У цьому випадку ми можемо визнати, що
\[−\dfrac{3}{8}=−\dfrac{3}{2}(\dfrac{1}{4})\]
Негативні три-восьмі - півтора рази на чверть, тому розміщуємо лінію, рухаючись за годинниковою стрілкою на одну повну чверть і половину іншої чверті, як на малюнку\(\PageIndex{9}\).
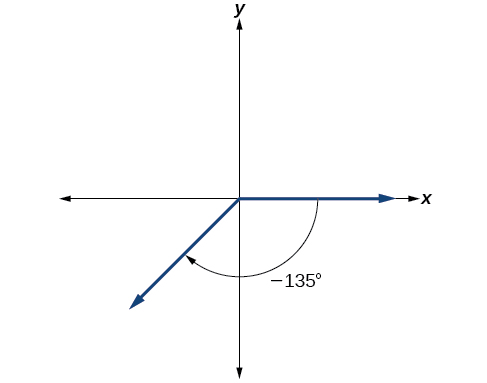
Малюнок\(\PageIndex{9}\)
\(\PageIndex{1}\):
Показувати кут 240° на колі в стандартному положенні.
Рішення
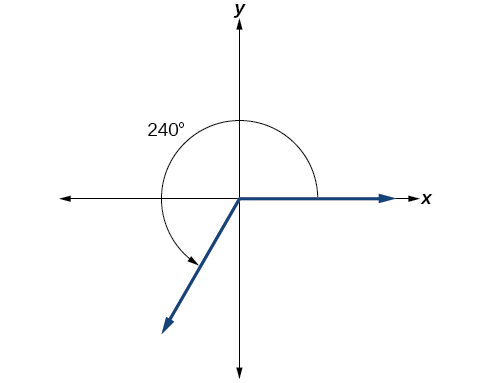
Перетворення між градусами та радіанами
Розділення кола на 360 частин - це довільний вибір, хоча він створює звичне вимірювання ступеня. Ми можемо вибрати інші способи поділу кола. Щоб знайти іншу одиницю, подумайте про процес малювання кола. Уявіть, що ви зупиняєтеся до того, як коло буде завершено. Частина, яку ви намалювали, називається дугою. Дуга може бути частиною повного кола, повного кола або більше повного кола, представленого більш ніж одним повним обертанням. Довжина дуги навколо всього кола називається окружністю цього кола.
Окружність кола дорівнює\(C=2πr\). Якщо розділити обидві сторони цього рівняння на\(r\), то створимо відношення окружності до радіуса, яке завжди\(2π\) незалежно від довжини радіуса. Таким чином, окружність будь-якого кола в\(2π≈6.28\) рази перевищує довжину радіуса. Це означає, що якби ми взяли рядок до радіуса і використали її для вимірювання послідовних довжин по колу, було б місце для шести повних довжин рядків і трохи більше чверті сьомої, як показано на малюнку\(\PageIndex{11}\).
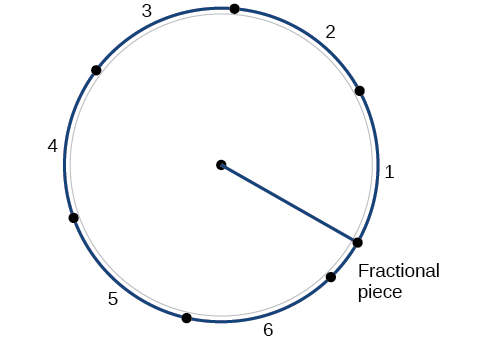
Це підводить нас до нашої нової міри кута. Один радіан - це міра центрального кута кола, який перехоплює дугу, рівну по довжині радіусу цього кола. Центральний кут - це кут, утворений в центрі кола двома радіусами. Оскільки загальна окружність дорівнює\(2π\) кращому радіусу, повне кругове обертання - це\(2π\) радіани. Так
\[\begin{align} 2π \text{ radians } & =360^∘ \\ π \text{ radians } & =\dfrac{360^∘}{2}=180^∘ \\ 1 \text{ radian } & =\dfrac{180^∘}{π}≈57.3^∘ \end{align}\]
Див\(\PageIndex{12}\). Малюнок. Зверніть увагу, що коли кут описується без певної одиниці, він відноситься до радіанової міри. Наприклад, кутова міра 3 вказує на 3 радіана. Насправді радіанове вимірювання є безрозмірним, оскільки це частка довжини (окружності), розділеної на довжину (радіус), а одиниці довжини скасовуються.
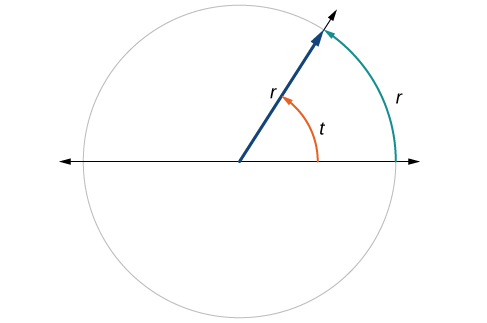
Віднесення довжин дуги до радіуса
Довжина дуги\(s\) - це довжина кривої вздовж дуги. Подібно до того, як повна окружність кола завжди має постійне відношення до радіуса, довжина дуги, вироблена будь-яким заданим кутом, також має постійне відношення до радіуса, незалежно від довжини радіуса.
Це співвідношення, яке називається радіановою мірою, однакове незалежно від радіуса кола - воно залежить тільки від кута. Ця властивість дозволяє визначити міру будь-якого кута як відношення довжини дуги s s до радіуса\(r\). Див\(\PageIndex{13}\). Малюнок.
\[\begin{align} s &=rθ \\ θ &=\dfrac{s}{r} \end{align}\]
Якщо\( s=r\), то\(θ=\frac{r}{r}= 1 \text{ radian.}\)
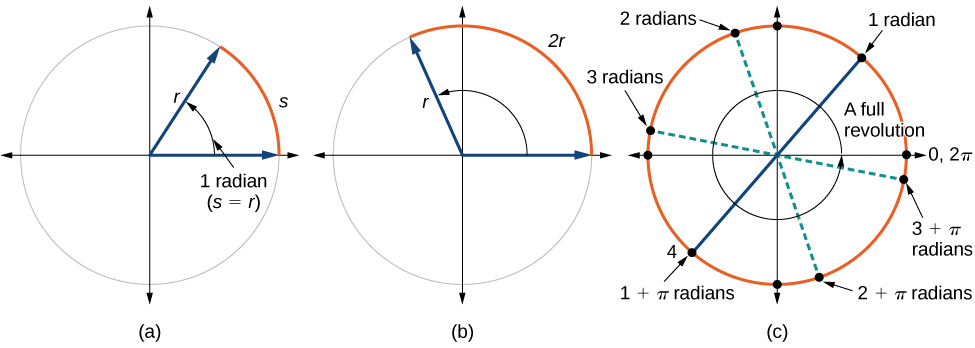
Щоб детально розглянути цю ідею, розглянемо два кола, один з радіусом 2, а інший з радіусом 3. Нагадаємо, окружність кола є\(C=2πr\), де\(r\) радіус. Менше коло має окружність,\(2π(2)=4π\) а більша має окружність\(2π(3)=6π\). Тепер ми малюємо кут 45° на двох колах, як на малюнку\(\PageIndex{14}\).
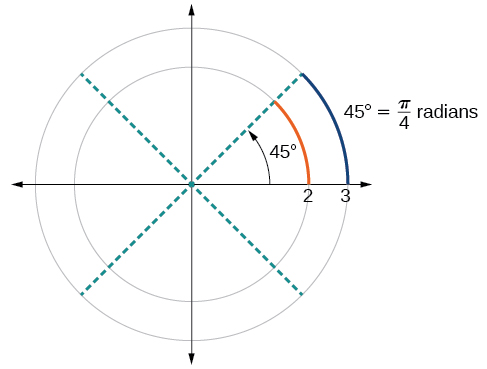
Зверніть увагу, що станеться, якщо ми знайдемо відношення довжини дуги, розділене на радіус кола.
\[\begin{align} \text{Smaller circle: } \dfrac{\frac{1}{2}π}{2} & =\dfrac{1}{4}π \\[2mm] \text{Larger circle: } \dfrac{\frac{3}{4}π}{3} & =\dfrac{1}{4}π \end{align}\]
Оскільки обидва співвідношення є\(\frac{1}{4}π\), вимірювання кута обох кіл однакові, хоча довжина дуги та радіус відрізняються.
РАДІАНИ
Один радіан - це міра центрального кута кола така, щоб довжина дуги між початковою стороною і кінцевою стороною дорівнювала радіусу кола. Повний оборот (360°) дорівнює\(2\pi\) радіанам. Половина обороту (180°) еквівалентна\(\pi\) радіанам.
Радіан міра кута - це відношення довжини дуги, піднесеної кутом до радіуса кола. Іншими словами, якщо\(s\) довжина дуги кола і радіус кола, то центральний кут, що містить цю дугу,\(r\) вимірює\(\frac{s}{r}\) радіани. У колі радіуса 1 радіанова міра відповідає довжині дуги.
Міра 1 радіан виглядає приблизно 60°. Це правильно?
Так. Це приблизно 57,3°. Оскільки \(2π\)радіани дорівнюють 360°,\(1\) радіан дорівнює\(\frac{360°}{2π}≈57.3°\).
Використання радіанів
Оскільки радіановна міра - це співвідношення двох довжин, це безодинична міра. Наприклад, на малюнку\(\PageIndex{14}\), припустимо, радіус становив 2 дюйми, а відстань по дузі також становило 2 дюйми. Коли ми обчислюємо радіанову міру кута, «дюйми» скасовуються, і ми отримуємо результат без одиниць. Тому не потрібно писати мітку «радіани» після радіанової міри, і якщо ми бачимо кут, який не позначений «градусами» або символом градуса, ми можемо припустити, що це радіанова міра.
Розглядаючи найосновніший випадок, одиничне коло (коло з радіусом 1), ми знаємо, що 1 обертання дорівнює 360 градусам, 360°. Ми також можемо відстежувати одне обертання навколо кола, знаходячи окружність\(C=2πr\), і для одиничного кола\(C=2π.\) Ці два різні способи обертання навколо кола дають нам спосіб перетворення з градусів в радіани.
\[\begin{array}{clll} 1 \text{rotation } & =360° & =2π & \text{radians} \\[2mm] \dfrac{1}{2} \text{rotation } & =180° & =π & \text{radians} \\[2mm] \dfrac{1}{4} \text{rotation } & =90° & =\dfrac{π}{2} & \text{radians} \end{array}\]
Визначення спеціальних кутів, виміряних в радіанах
Окрім знання вимірювань у градусах та радіанах чверті обороту, півобороту та повного обороту, є й інші часто зустрічаються кути в одному обороті кола, з якими ми повинні бути знайомі. Зазвичай зустрічаються кратні 30, 45, 60 та 90 градусам. Ці значення наведені на рис\(\PageIndex{15}\). Запам'ятовування цих кутів буде дуже корисно, оскільки ми вивчаємо властивості, пов'язані з кутами.
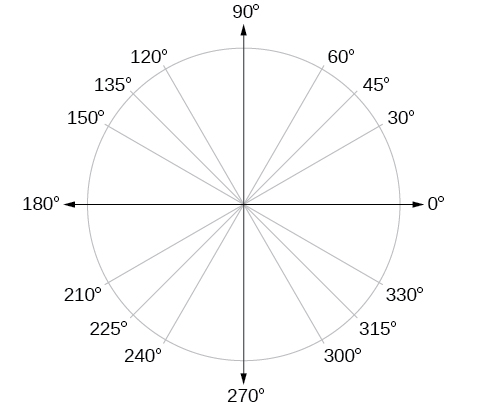
Тепер ми можемо перерахувати відповідні значення радіана для загальних мір кола, відповідних тим, що перераховані на малюнку\(\PageIndex{15}\), які наведені на малюнку\(\PageIndex{16}\). Переконайтеся, що ви можете перевірити кожну з цих заходів.
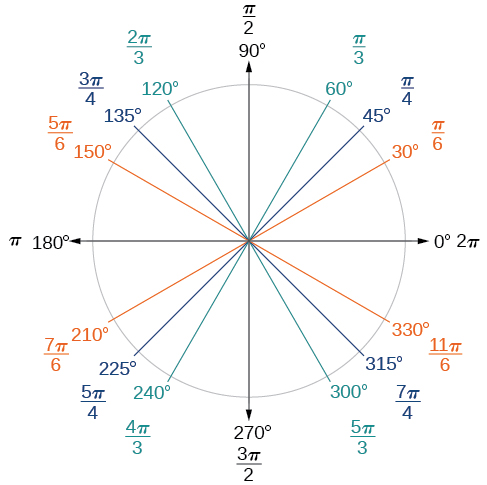
Приклад\(\PageIndex{2}\): Finding a Radian Measure
Знайдіть радіанову міру однієї третини повного обертання.
Рішення
Для будь-якого кола довжина дуги по такому обертанню становила б одну третину окружності. Ми знаємо, що
\[1 \text{ rotation}=2πr\]
Отже,
\[\begin{align}s &= \dfrac{1}{3}(2πr) \\[2mm] &=\dfrac{2πr}{3} \end{align}\]
Радіан мірою буде довжина дуги, розділена на радіус.
\[\begin{align} \text{radian measure} & = \dfrac{\frac{2πr}{3}}{r} \\[2mm] &= \dfrac{2πr}{3r} \\[2mm] & = \dfrac{2π}{3} \end{align}\]
\(\PageIndex{2}\)
Знайдіть радіанову міру трьох чверті повного обертання.
Рішення
\[\dfrac{3π}{2}\]
Перетворення між радіанами та градусами
Оскільки градуси та радіани вимірюють кути, ми повинні мати можливість конвертувати між ними. Ми можемо легко зробити це, використовуючи пропорцію.
\[\dfrac{θ}{180}=\dfrac{θ^R}{π}\]
Ця пропорція показує, що міра кута\(θ\) в градусах розділена на 180 дорівнює мірі кута\(θ\) в радіанах, розділених на\(π.\) Або, по-іншому, градуси до 180, як радіани\(π\).
\[\dfrac{\text{Degrees}}{180}=\dfrac{Radians}{π} \]
ПЕРЕТВОРЕННЯ МІЖ РАДІАНАМИ І ГРАДУСАМИ
Для перетворення між градусами і радіанами використовуйте пропорцію
\[\dfrac{θ}{180}=\dfrac{θ^R}{π}\]
Приклад\(\PageIndex{3}\): Converting Radians to Degrees
Перетворіть кожну радіановну міру в градуси.
- \(\frac{π}{6}\)
- 3
Рішення
Оскільки нам дають радіани і ми хочемо градусів, ми повинні встановити пропорцію і вирішити її.
- Використовуємо пропорцію, підставляючи задану інформацію.
\[\begin{align}\dfrac{θ}{180} &=\dfrac{θ^R}{π} \\[2mm] \dfrac{θ}{180} & =\dfrac{\frac{π}{6}}{π} \\ θ & =\dfrac{180}{6} \\ θ & =30^∘ \end{align}\]
- Використовуємо пропорцію, підставляючи задану інформацію.
\[\begin{align}\dfrac{θ}{180} &= \dfrac{θ^R}{π} \\ \dfrac{θ}{180} &=\dfrac{3}{π} \\ θ &= \dfrac{3(180)}{π} \\ θ & ≈172^∘ \end{align}\]
\(\PageIndex{3}\)
Перетворення\(−\frac{3π}{4}\) радіанів в градуси.
Рішення
−135°
Приклад\(\PageIndex{4}\): Converting Degrees to Radians
Перетворення\(15\) градусів в радіани.
Рішення
У цьому прикладі ми починаємо з градусів і хочемо радіани, тому ми знову встановлюємо пропорцію і вирішуємо її, але ми підставляємо дану інформацію в іншу частину пропорції.
\[\begin{align}\dfrac{θ}{180} &= \dfrac{θ^R}{π} \\ \dfrac{15}{180} &=\dfrac{θ^R}{π} \\ \dfrac{15π}{180} & =θ^R \\ \dfrac{π}{12} & =θ^R \end{align}\]
Аналіз
Ще один спосіб подумати про цю проблему - пам'ятати про це\(30^∘=\frac{π}{6}\). Тому що\(15^∘=\frac{1}{2}(30^∘)\), ми можемо знайти, що\(\frac{1}{2}(\frac{π}{6})\) є\(\frac{π}{12}\).
\(\PageIndex{4}\)
Перетворити 126° на радіани.
Рішення
\(\frac{7π}{10}\)
Пошук котермінальних кутів
Перетворення між градусами та радіанами може полегшити роботу з кутами в деяких додатках. Для інших додатків нам може знадобитися інший тип перетворення. Негативні кути та кути, більші за повний оборот, більш незручні для роботи, ніж ті, що знаходяться в діапазоні від 0° до 360°, або від 0 до\(2π\). Було б зручно замінити ті кути поза діапазоном діапазону відповідним кутом в межах одного обороту.
Можна для більш ніж одного кута мати однакову сторону терміналу. Подивіться на Малюнок\(\PageIndex{17}\). Кут 140° - це позитивний кут, виміряний проти годинникової стрілки. Кут —220° - це негативний кут, вимірюваний за годинниковою стрілкою. Але обидва кути мають однакову кінцеву сторону. Якщо два кути в стандартному положенні мають однакову кінцеву сторону, вони є котермінальними кутами. Кожен кут більше 360° або менше 0° є співтермінальним з кутом між 0° і 360°, і часто зручніше знайти котермінальний кут в діапазоні від 0° до 360°, ніж працювати з кутом, який знаходиться поза цим діапазоном.
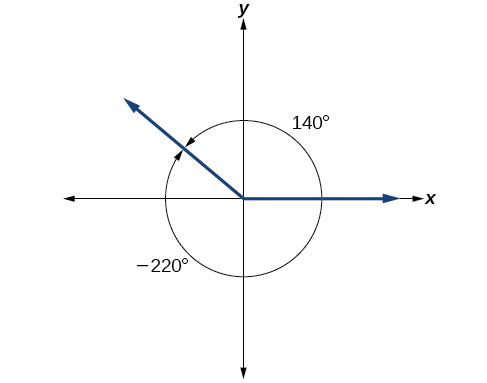
Будь-який кут має нескінченно багато котермінальних кутів, тому що кожен раз, коли ми додаємо 360° до цього кута - або віднімаємо 360° від нього - отримане значення має кінцеву сторону в тому ж місці. Наприклад, 100° і 460° є співтермінальними з цієї причини, як і −260°. Визнання того, що будь-який кут має нескінченно багато котермінальних кутів, пояснює повторювану форму на графіках тригонометричних функцій.
Опорний кут кута - це міра найменшого, позитивного, гострого кута,\(t\) утвореного кінцевою стороною кута\(t\) та горизонтальною віссю. Таким чином, позитивні опорні кути мають кінцеві сторони, які лежать у першому квадранті і можуть бути використані як моделі для кутів в інших квадрантах. Див. Рисунок\(\PageIndex{18}\) для прикладів опорних кутів для кутів у різних квадрантах.
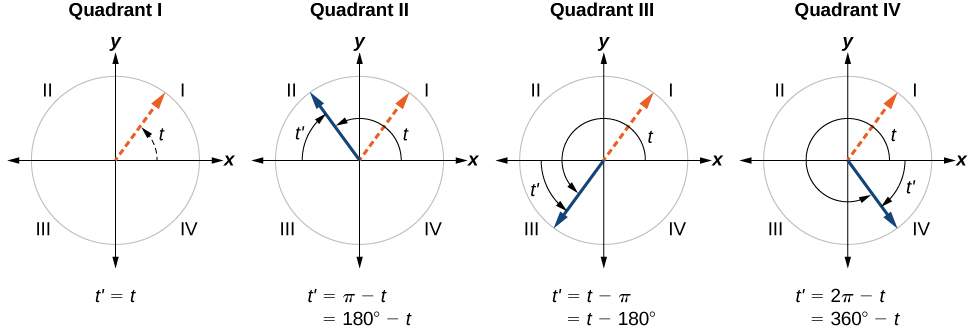
КОТЕРМІНАЛ І ОПОРНІ КУТИ
- Котермінальні кути - це два кути в стандартному положенні, які мають однакову кінцеву сторону.
- Опорний кут кута - це розмір найменшого гострого кута\(t′\), утвореного кінцевою стороною кута\(t\) та горизонтальною віссю.
Враховуючи кут, більший за 360°, знайдіть котермінальний кут між 0° та 360°
- Відніміть 360° від заданого кута.
- Якщо результат все ще перевищує 360°, знову відніміть 360°, поки результат не буде між 0° і 360°.
- Отриманий кут співвідноситься з початковим кутом.
Приклад\(\PageIndex{5}\): Finding an Angle Coterminal with an Angle of Measure Greater Than 360°
Знайти найменший позитивний кут θ, який є співтермінальним з кутом вимірювання 800°, де\(0°≤θ<360°\).
Рішення
Кут з мірою 800° є співтермінальним з кутом з мірою 800 − 360 = 440°, але 440° все ще більше 360°, тому ми знову віднімаємо 360°, щоб знайти інший котермінальний кут: 440 − 360 = 80°.
\(θ=80°\)Кут співтермінальний з 800°. Іншим чином, 800° дорівнює 80° плюс два повних обертання, як показано на малюнку\(\PageIndex{19}\).
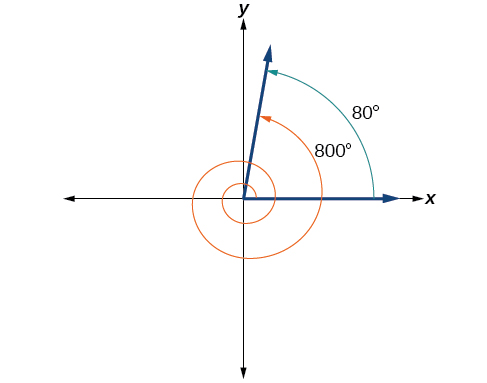
\(\PageIndex{5}\)
Знайдіть кут\(α\), який є співтермінальним з кутом вимірювання 870°, де\(0°≤α<360°\).
Рішення
\(α=150°\)
Враховуючи кут з мірою менше 0°, знайдіть котермінальний кут, який має міру від 0° до 360°.
- Додайте 360° до заданого кута.
- Якщо результат все ще менше 0°, додайте 360° ще раз, поки результат не стане між 0° і 360°.
- Отриманий кут співвідноситься з початковим кутом.
Приклад\(\PageIndex{6}\): Finding an Angle Coterminal with an Angle Measuring Less Than 0°
Покажіть кут з мірою −45° на колі та знайдіть додатний співтермінальний кут α такий, що 0° ≤ α < 360°.
Рішення
Оскільки 45° становить половину 90°, ми можемо почати з позитивної горизонтальної осі і вимірювати за годинниковою стрілкою половину кута 90°.
Оскільки ми можемо знайти котермінальні кути, додаючи або віднімаючи повне обертання на 360°, ми можемо знайти позитивний котермінальний кут тут, додавши 360°:
\[−45°+360°=315°\]
Потім ми можемо показати кут на колі, як на малюнку\(\PageIndex{20}\).
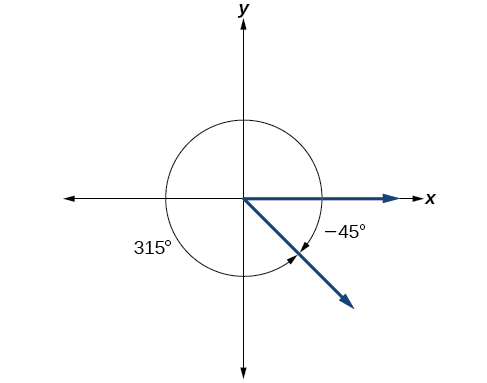
\(\PageIndex{6}\)
Знайти кут β, який є співтермінальним з кутом вимірювання −300° таким, що\(0°≤β<360°\).
Рішення
\(β=60°\)
Пошук котермінальних кутів, виміряних в радіанах
Ми можемо знайти котермінальні кути, виміряні в радіанах приблизно так само, як ми знайшли їх за допомогою градусів. В обох випадках ми знаходимо котермінальні кути шляхом додавання або віднімання одного або декількох повних обертань.
З огляду на кут більше\(2\pi\), find a coterminal angle between 0 and \(2\pi\).
- Відняти\(2π\) від заданого кута.
- Якщо результат все ще більше\(2π\), відніміть ще\(2π\) раз, поки результат не буде між\(0\) і\(2π\).
- Отриманий кут співвідноситься з початковим кутом.
Приклад\(\PageIndex{7}\): Finding Coterminal Angles Using Radians
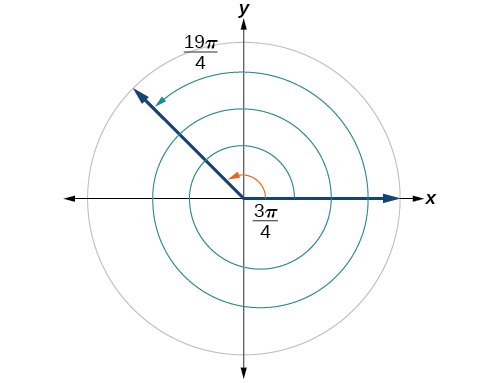
Знайти кут\(β\), який є співтермінальним з\(\frac{19π}{4}\), де\(0≤β<2π.\)
Рішення
При роботі в градусах ми знайшли котермінальні кути, додаючи або віднімаючи 360 градусів, повне обертання. Так само в радіанах ми можемо знайти котермінальні кути, додаючи або віднімаючи повні обертання\(2π\) радіанів:
\[\begin{align} \dfrac{19π}{4}−2π & =\dfrac{19π}{4}−\dfrac{8π}{4} \\ &=\dfrac{11π}{4} \end{align}\]
\(\frac{11π}{4}\)Кут співтермінальний, але не менше\(2π\), тому віднімаємо ще одне обертання:
\[\begin{align} \dfrac{11π}{4}−2π &= \dfrac{11π}{4}−\dfrac{8π}{4} \\ &= \dfrac{3π}{4} \end{align}\]
Кут\(\frac{3π}{4}\) співтермінальний з\(\frac{19π}{4}\), як показано на малюнку\(\PageIndex{21}\).
\(\PageIndex{7}\)
Знайти кут вимірювання\(θ\), який є співтермінальним з кутом вимірювання\(−\frac{17π}{6}\), де\(0≤θ<2π.\)
Рішення
\(\frac{7π}{6}\)
Визначення довжини дуги
Нагадаємо, що \(θ\)радіанову міру кута визначали як відношення довжини\(s\) дуги дуги окружності до радіуса\(r\) кола,\(θ=\frac{s}{r}\). З цієї залежності ми можемо знайти довжину дуги по колу, заданий кут.
ДОВЖИНА ДУГИ ПО КОЛУ
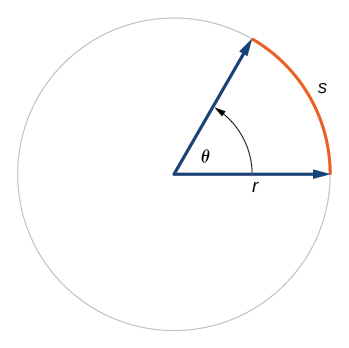
У колі радіуса r довжина дуги,\(s\) піднесеної кутом з мірою\(θ\) в радіанах, показана на малюнку\(\PageIndex{22}\), дорівнює
\[s=rθ\]
Задано коло радіуса\(r,\) calculate the length \(s\) of the arc subtended by a given angle of measure \(θ\).
- При необхідності перетворити\(θ\) в радіани.
- Помножте радіус\(r\) на радіанову міру\(θ:s=rθ\).
Приклад\(\PageIndex{8}\): Finding the Length of an Arc
Припустимо, орбіта Меркурія навколо Сонця є ідеальним колом. Меркурій знаходиться приблизно в 36 мільйонів миль від сонця.
- За один земний день Меркурій завершує 0.0114 свого повного обороту. Скільки миль він проїжджає за один день?
- Використовуйте свою відповідь з частини (а), щоб визначити радіанову міру руху Меркурія за один день Землі.
Рішення
- Почнемо з пошуку окружності орбіти Меркурія.
\[\begin{align} C &=2πr \\ &=2π(\text{36 million miles}) \\ &≈226 \text{ million miles} \end{align}\]
Оскільки Меркурій завершує 0.0114 свого загального обороту за один день Землі, тепер ми можемо знайти пройдену відстань:
\[(0.0114)226 \text{ million miles} = 2.58 \text{ million miles}\]
- Тепер ми перетворюємо в радіани:
\[\begin{align} \text{radian} & = \dfrac{\text{arc length}}{\text{radius}} \\ &= \dfrac{2.58 \text{ million miles}}{36 \text{ million miles}} \\ & =0.0717 \end{align} \]
\(\PageIndex{8}\)
Знайдіть довжину дуги по колу радіусом 10 одиниць, піднесених кутом 215°.
Рішення
\[\dfrac{215π}{18}=37.525 \text{ units} \]
Знаходження площі сектора кола
Окрім довжини дуги, ми також можемо використовувати кути, щоб знайти площу сектора кола. Сектор - це область кола, обмежена двома радіусами і перехопленою дугою, як шматочок піци або пирога. Нагадаємо, що площа кола з радіусом\(r\) можна знайти за формулою\(A=πr^2\). Якщо два радіуси утворюють кут\(θ\), виміряний в радіанах, то\(\frac{θ}{2π}\) це відношення міри кута до міри повного обертання і також є, отже, відношення площі сектора до площі кола. Таким чином, площа сектора - це дріб,\(\frac{θ}{2π}\) помножений на всю площу. (Завжди пам'ятайте, що ця формула\(θ\) застосовується лише в радіанах.)
\[\begin{align} \text{Area of sector} & =(\dfrac{θ}{2π})πr^2 \\ &=\dfrac{θπr^2}{2π} \\ & =\dfrac{1}{2}θr^2 \end{align}\]
ПЛОЩА СЕКТОРА
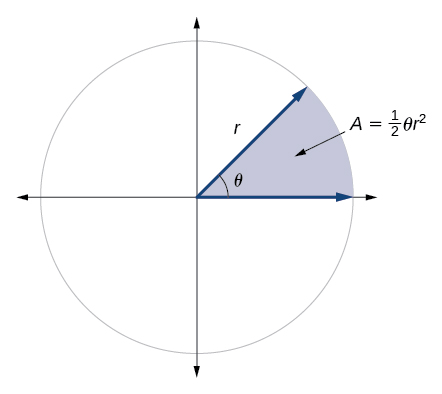
Площа сектора кола з радіусом,\(r\) піднесеного кутом\(θ\), вимірюється в радіанах, дорівнює
\[A=\dfrac{1}{2}θr^2\]
Див\(\PageIndex{23}\). Малюнок.
Задано коло радіуса\(r,\) find the area of a sector defined by a given angle \(θ.\)
- При необхідності перетворити\(θ\) в радіани.
- Помножте половину радіановної міри\(θ\) на квадрат радіуса\(r: A=\frac{1}{2}θr^2.\)
Приклад\(\PageIndex{9}\): Finding the Area of a Sector
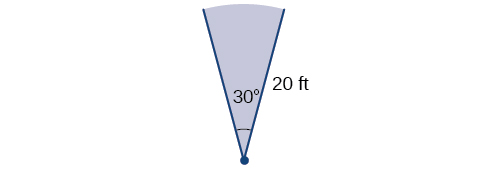
Автоматичний спринклер для газону розпилює відстань 20 футів при обертанні на 30 градусів, як показано на малюнку\(\PageIndex{24}\). Яка площа сектора трави спринклерних вод?
Рішення
По-перше, нам потрібно перетворити міру кута в радіани. Оскільки 30 градусів є одним із наших спеціальних кутів, ми вже знаємо еквівалентну радіанову міру, але ми також можемо перетворити:
\[\begin{align} \text{30 degrees} &=30⋅\frac{π}{180} \\ &=\frac{π}{6} \text{ radians} \end{align}\]
Площа сектору тоді
\[\begin{align} \text{Area} &= \dfrac{1}{2}(\dfrac{π}{6})(20)^2 \\ & ≈104.72 \end{align}\]
Так що площа приблизно\(\mathrm{104.72 \; ft^2}\).
\(\PageIndex{9}\)
У центральному шарнірному зрошенні велика зрошувальна труба на колесах обертається навколо центральної точки. Фермер має центральну систему шарнірів радіусом 400 метрів. Якщо водні обмеження дозволяють їй лише поливати 150 тисяч квадратних метрів на добу, який кут вона повинна встановлювати для покриття системи? Запишіть відповідь радіановою мірою до двох знаків після коми.
Рішення
1.88
Використовуйте лінійну та кутову швидкість для опису руху на круговому шляху
Окрім пошуку площі сектора, ми можемо використовувати кути для опису швидкості рухомого об'єкта. Об'єкт, що рухається по круговому шляху, має два типи швидкості. Лінійна швидкість - це швидкість по прямому шляху і може бути визначена по відстані, по якій вона рухається (її зміщенню) в заданий часовий проміжок. Наприклад, якщо колесо з радіусом 5 дюймів обертається один раз в секунду, точка на краю колеса рухається відстань, рівну окружності, або 10π дюймів, кожну секунду. Таким чином, лінійна швидкість точки знаходиться\(10π\) в. /s. рівняння для лінійної швидкості виглядає наступним чином, де\(v\) лінійна швидкість,\(s\) є зміщення, і\(t\) час.
\[v=\dfrac{s}{t}\]
Кутова швидкість виникає в результаті кругового руху і може бути визначена за кутом, через який точка обертається в заданий проміжок часу. Іншими словами, кутова швидкість - це кутове обертання в одиницю часу. Так, наприклад, якщо передача здійснює повне обертання кожні 4 секунди, ми можемо обчислити її кутову швидкість як\(\frac{360 \text{ degrees}}{4 \text{ seconds}}= \) 90 градусів в секунду. Кутова швидкість може бути вказана в радіанах в секунду, обертаннях в хвилину або градусах на годину, наприклад. Рівняння кутової швидкості виглядає наступним чином, де\(ω\) (читається як омега) - кутова швидкість,\(θ\) - кут, пройдений, і\(t\) є час.
\[ω=\dfrac{θ}{t}\]
Поєднуючи визначення кутової швидкості з рівнянням довжини дуги\(s=rθ\), ми можемо знайти залежність між кутовою і лінійною швидкостями. Рівняння кутової швидкості можна вирішити для\(θ\),\(θ=ωt.\) даючи Заміна цього в рівняння довжини дуги дає:
\[\begin{align}s &=rθ \\ &=rωt \end{align}\]
Підставляючи це в лінійне рівняння швидкості, дає:
\[\begin{align} v & = \dfrac{s}{t} &=\dfrac{rωt}{t} &=rω \end{align}\]
КУТОВА І ЛІНІЙНА ШВИДКІСТЬ
Як точка рухається по колу радіуса\(r,\) його кутова швидкість,\(ω\), є кутовим обертанням\(θ\) в одиницю часу,\(t\).
\[ω=\dfrac{θ}{t}\]
Лінійна швидкість. \(v\), точки можна знайти як пройдену відстань, довжину дуги\(s\), за одиницю часу,\(t.\)
\[v=\frac{s}{t}\]
Коли кутова швидкість вимірюється в радіанах в одиницю часу, лінійна швидкість і кутова швидкість пов'язані рівнянням
\[v=rω\]
Це рівняння стверджує, що кутова швидкість в радіанах\(ω\), що представляє величину обертання, що відбувається за одиницю часу, може бути помножена на радіус\(r\) для обчислення загальної довжини дуги, пройденої за одиницю часу, що є визначенням лінійної швидкості.
З огляду на величину кута повороту і минулий час, обчисліть кутову швидкість
- При необхідності перетворіть кутову міру в радіани.
- Розділіть кут в радіанах на кількість минулих одиниць часу:\(ω=\frac{θ}{t}.\)
- Отримана швидкість буде в радіанах за одиницю часу.
Приклад\(\PageIndex{10}\): Finding Angular Speed
Водяне колесо, показане на малюнку\(\PageIndex{25}\), завершує 1 обертання кожні 5 секунд. Знайти кутову швидкість в радіанах в секунду.
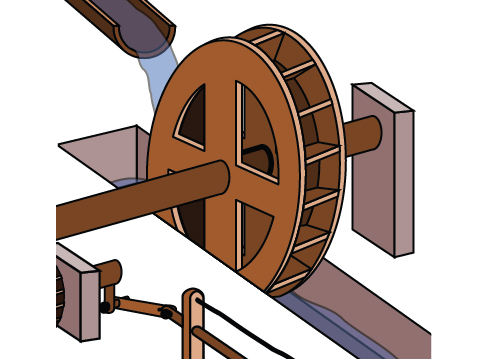
Рішення
Колесо завершує обертання 1, або проходить через кут\(2π\) радіанів за 5 секунд, тому кутова швидкість буде\(ω=\frac{2π}{5}≈1.257\) радіани в секунду.
\(\PageIndex{10}\)
Стара вінілова платівка відтворюється на поворотному столі, що обертається за годинниковою стрілкою зі швидкістю 45 обертів в хвилину. Знайти кутову швидкість в радіанах в секунду.
Рішення
\(−\frac{3π}{2}\)рад/с
Враховуючи радіус кола, кут повороту та довжину часу, що минув, визначають лінійну швидкість
- Перетворіть загальне обертання в радіани, якщо це необхідно.
- Розділіть сумарне обертання в радіанах на минулий час, щоб знайти кутову швидкість: застосувати\(ω=\frac{θ}{t}\).
- Помножте кутову швидкість на довжину радіуса, щоб знайти лінійну швидкість, виражену через одиницю довжини, яка використовується для радіуса, і одиниці часу, що використовується за минулий час: застосувати\(v=rω\).
Приклад\(\PageIndex{11}\): Finding a Linear Speed
Велосипед має колеса діаметром 28 дюймів. Тахометр визначає, що колеса обертаються зі швидкістю 180 об/хв (оборотів в хвилину). Знайти швидкість велосипед їде вниз по дорозі.
Рішення
Тут у нас кутова швидкість і потрібно знайти відповідну лінійну швидкість, так як лінійна швидкість зовнішньої сторони шин - це швидкість, з якою велосипед їде по дорозі.
Ми починаємо з перетворення з обертань в хвилину в радіани в хвилину. Це може бути корисно використовувати одиниці, щоб зробити це перетворення:
\[\mathrm{180 \dfrac{\cancel{rotations}}{minute}⋅\dfrac{2π \; radians}{\cancel{rotation}}=360π\dfrac{radians}{minute}}\]
Використовуючи формулу зверху разом з радіусом коліс, ми можемо знайти лінійну швидкість:
\[\begin{align} v & =(14 \text{ inches})(360π \dfrac{\text{radians}}{\text{minute}}) \\ &=5040π \dfrac{\text{inches}}{\text{minute}} \end{align}\]
Пам'ятайте, що радіани - це безодинична міра, тому включати їх необов'язково необов'язково, тому включати їх необов'язково.
Нарешті, ми можемо захотіти перетворити цю лінійну швидкість в більш звичне вимірювання, наприклад, милі на годину.
\[\mathrm{5040π\dfrac{\cancel{inches}}{\cancel{minute}}⋅\dfrac{1 \; \cancel{ feet}}{12 \; \cancel{ inches}}⋅\dfrac{1 \; \cancel{ mile}}{5280 \cancel{ feet}}⋅\dfrac{60 \cancel{ minutes}}{1 \; hour}≈14.99 \; miles \; per \; hour \; (mph)}\]
![]() \(\PageIndex{11}\)
\(\PageIndex{11}\)
Супутник обертається навколо Землі зі швидкістю 0,25 радіанів на годину на висоті 242 км над Землею. Якщо радіус Землі становить 6378 кілометрів, знайдіть лінійну швидкість супутника в кілометрах на годину.
Рішення
1655 кілометрів на годину
Медіа
Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з кутами, довжиною дуги та областями секторів.
Ключові рівняння
| довжина дуги | \(s=rθ\) |
| area of a sector | \(A=\frac{1}{2}θr^2\) |
| angular speed | \(ω=\frac{θ}{t}\) |
| linear speed | \(v=\frac{s}{t}\) |
| linear speed related to angular speed | \(v=rω\) |
Key Concepts
- An angle is formed from the union of two rays, by keeping the initial side fixed and rotating the terminal side. The amount of rotation determines the measure of the angle.
- An angle is in standard position if its vertex is at the origin and its initial side lies along the positive x-axis. A positive angle is measured counterclockwise from the initial side and a negative angle is measured clockwise.
- To draw an angle in standard position, draw the initial side along the positive x-axis and then place the terminal side according to the fraction of a full rotation the angle represents. See Example.
- In addition to degrees, the measure of an angle can be described in radians. See Example.
- To convert between degrees and radians, use the proportion \(\frac{θ}{180}=\frac{θ^R}{π}\). See Example and Example.
- Two angles that have the same terminal side are called coterminal angles.
- We can find coterminal angles by adding or subtracting 360° or \(2π\). See Example and Example.
- Coterminal angles can be found using radians just as they are for degrees. See Example.
- The length of a circular arc is a fraction of the circumference of the entire circle. See Example.
- The area of sector is a fraction of the area of the entire circle. See Example.
- An object moving in a circular path has both linear and angular speed.
- The angular speed of an object traveling in a circular path is the measure of the angle through which it turns in a unit of time. See Example.
- The linear speed of an object traveling along a circular path is the distance it travels in a unit of time. See Example.
Glossary
- angle
- the union of two rays having a common endpoint
- angular speed
- the angle through which a rotating object travels in a unit of time
- arc length
- the length of the curve formed by an arc
- area of a sector
- area of a portion of a circle bordered by two radii and the intercepted arc; the fraction \(\frac{θ}{2π}\) multiplied by the area of the entire circle
- coterminal angles
- description of positive and negative angles in standard position sharing the same terminal side
- degree
- a unit of measure describing the size of an angle as one-360th of a full revolution of a circle
- initial side
- the side of an angle from which rotation begins
- linear speed
- the distance along a straight path a rotating object travels in a unit of time; determined by the arc length
- measure of an angle
- the amount of rotation from the initial side to the terminal side
- negative angle
- description of an angle measured clockwise from the positive x-axis
- positive angle
- description of an angle measured counterclockwise from the positive x-axis
- quadrantal angle
- an angle whose terminal side lies on an axis
- radian measure
- the ratio of the arc length formed by an angle divided by the radius of the circle
- radian
- the measure of a central angle of a circle that intercepts an arc equal in length to the radius of that circle
- ray
- one point on a line and all points extending in one direction from that point; one side of an angle
- reference angle
- the measure of the acute angle formed by the terminal side of the angle and the horizontal axis
- standard position
- the position of an angle having the vertex at the origin and the initial side along the positive x-axis
- terminal side
- the side of an angle at which rotation ends
- vertex
- the common endpoint of two rays that form an angle
