4.4: Теорема Піфагора

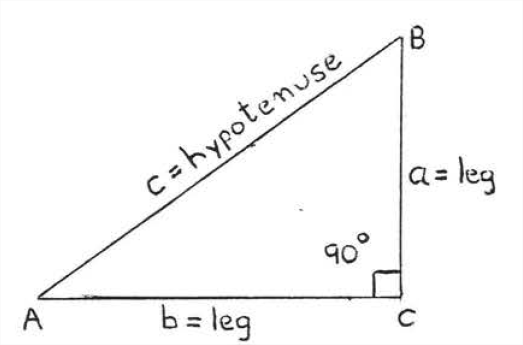
У прямокутному трикутнику сторони прямого кута називаються катетами трикутника, а решта - гіпотенузою. На малюнку$\PageIndex{1}$ бічні$AC$ і$BC$ є катетами, а сторона$AB$ - гіпотенуза.

Малюнок$\PageIndex{1}$: Прямокутний трикутник.

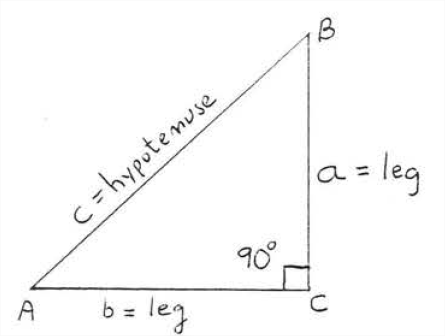
Нижче наведена одна з найвідоміших теорем з математики.

Теорема$\PageIndex{1}$: Pythagorean Theorem

У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів. Тобто,

$$\text{leg}^{2}+\text{leg}^{2}=\text{hypotenuse}^{2}$$

Таким чином, для сторін трикутника на малюнку$\PageIndex{1}$,

$$a^{2}+b^{2}=c^{2} \nonumber$$

Перш ніж довести Теорему$\PageIndex{1}$, наведемо кілька прикладів.

Приклад$\PageIndex{1}$

Знайти$x$

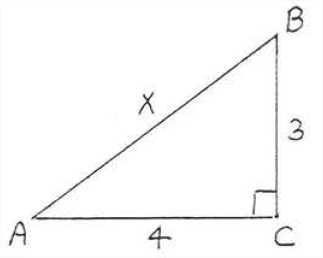
Рішення

$\begin{array} {rcl} {\text{leg}^2 + \text{leg}^2} & = & {\text{hyp}^2} \\ {3^2 + 4^2} & = & {x^2} \\ {9 + 16} & = & {x^2} \\ {25} & = & {x^2} \\ {5} & = & {x} \end{array}$

Перевірка:

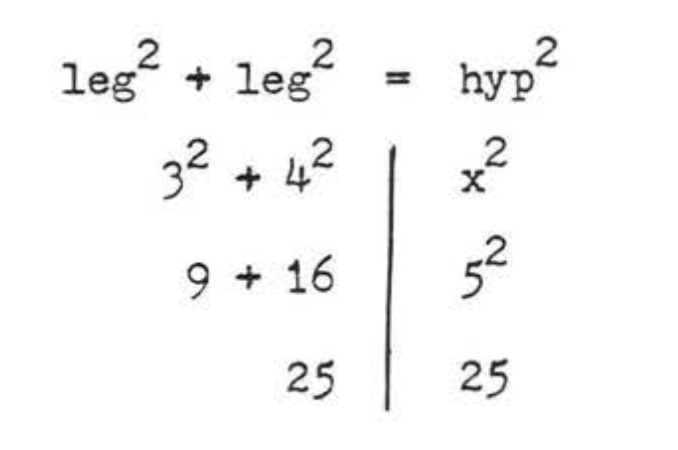
Відповідь:$x = 5$.

Приклад$\PageIndex{2}$

Знайти$x$:

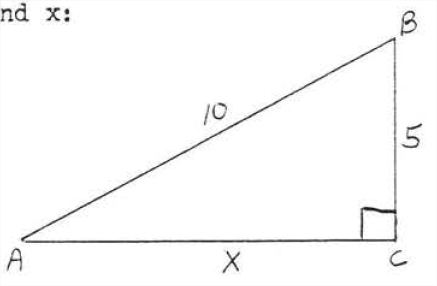
Рішення

$\begin{array} {rcl} {\text{leg}^2 + \text{leg}^2} & = & {\text{hyp}^2} \\ {5^2 + x^2} & = & {10^2} \\ {25 + x^2} & = & {100} \\ {x^2} & = & {75} \\ {x} & = & {\sqrt{75} = \sqrt{25} \sqrt{3} = 5\sqrt{3}} \end{array}$

Перевірка:

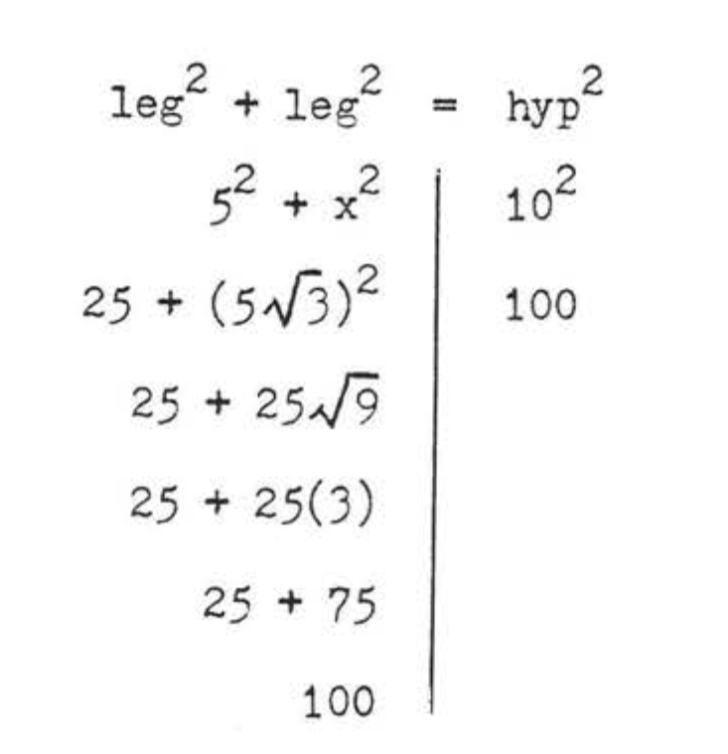
Відповідь:$x = 5\sqrt{3}$.

Приклад$\PageIndex{3}$

Знайти$x$:

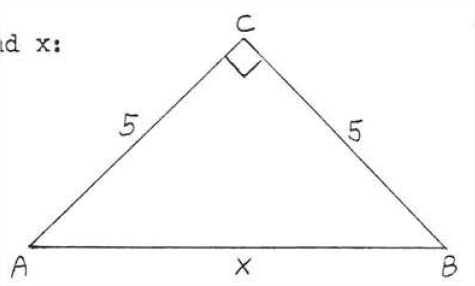
Рішення

$\begin{array} {rcl} {\text{leg}^2 + \text{leg}^2} & = & {\text{hyp}^2} \\ {5^2 + 5^2} & = & {x^2} \\ {25 + 25} & = & {x^2} \\ {50} & = & {x^2} \\ {x} & = & {\sqrt{50} = \sqrt{25} \sqrt{2} = 5\sqrt{2}} \end{array}$

Перевірка:

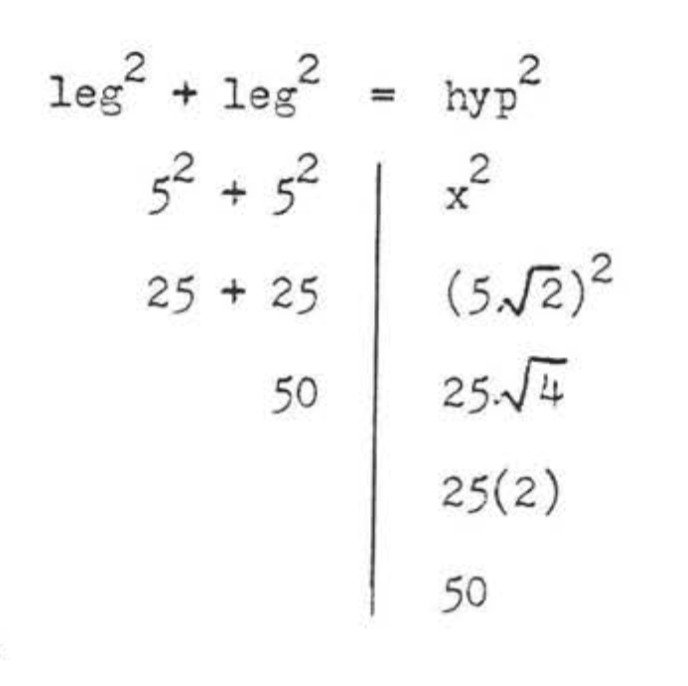
Відповідь:$x = 5\sqrt{2}$.

Приклад$\PageIndex{4}$

Знайти$x$

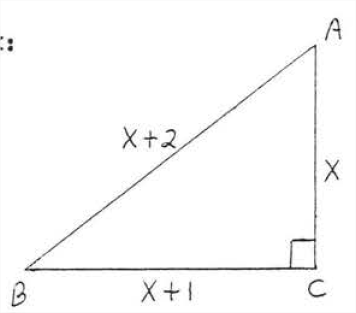
Рішення

$\begin{array} {rcl} {\text{leg}^2 + \text{leg}^2} & = & {\text{hyp}^2} \\ {x^2 + (x + 1)^2} & = & {(x + 2)^2} \\ {x^2 + x^2 + 2x + 1} & = & {x^2 + 4x + 4} \\ {x^2 + x^2 + 2x + 1 - x^2 - 4x - 4} & = & {0} \\ {x^2 - 2x - 3} & = & {0} \\ {(x - 3)(x + 1)} & = & {0} \end{array}$

$\begin{array} {rcl} {x - 3} & = & {0} \\ {x} & = & {3} \end{array}$$\begin{array} {rcl} {x + 1} & = & {0} \\ {x} & = & {-1} \end{array}$

Ми відкидаємо$x = -1$, тому що$AC = x$ не може бути негативним.

Перевірка,$x = 3$:

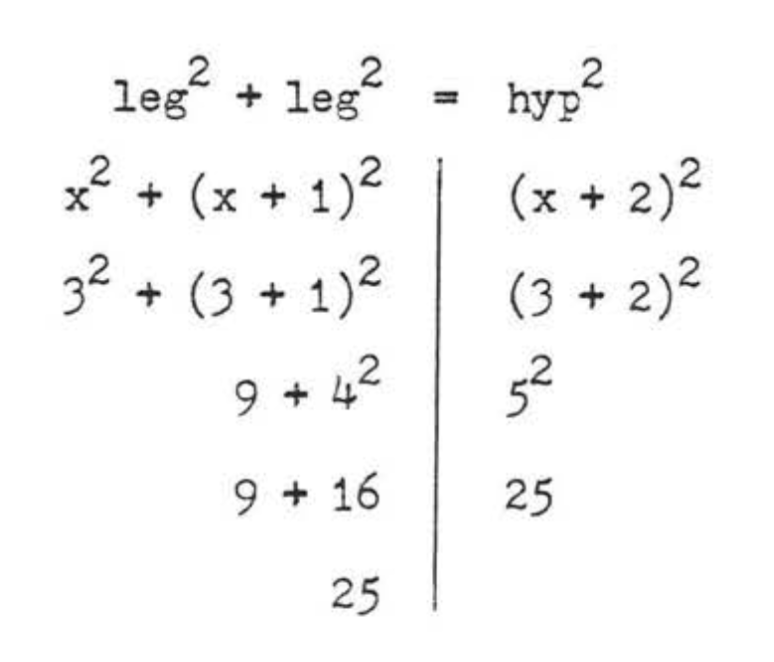
Відповідь:$x = 3$.

Тепер ми перекажемо і доведемо теорему$\PageIndex{1}$:

Теорема$\PageIndex{1}$ Pythagorean Theorem

У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів. Тобто,

$\text{leg}^2 + \text{leg}^2 = \text{hypotenuse}^2.$

На малюнку$\PageIndex{1}$,

$a^2 + b^2 = c^2.$

Малюнок$\PageIndex{1}$. A right triangle.

Малюнок$\PageIndex{2}$. Draw $CD$ perpendicular to $AB$.

Доказ

На малюнку$\PageIndex{1}$, draw $CD$ perpendicular to $AB$. Let $x = AD$. Then $BD = c - x$ (Figure $\PageIndex{2}$). As in Example $\PageIndex{3}$, section 4.2, $\triangle ABC \sim \triangle ACD$ and $\triangle ABC \sim \triangle CBD$. From these two similarities we obtain two proportions:

Зворотна теорема Піфагора також містить:

Теорема$\PageIndex{2}$ (converse of the Pythagorean Theorem).

In a triangle, if the square of one side is equal to the sun of the squares of the other two sides then the triangle is a right triangle.

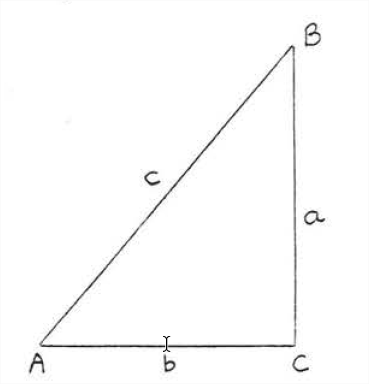
In Figure $\PageIndex{3}$, if $c^2 = a^2 + b^2$ then $\triangle ABC$ is a right triangle with $\angle C = 90^{\circ}$.

Figure $\PageIndex{3}$: If $c^2 = a^2 + b^2$ then $\angle C = 90^{\circ}$.

Proof

Draw a new triangle, $\triangle DEF$, so that $\angle F = 90^{\circ}$, $d = a$, and $e = b$ (Figure $\PageIndex{4}$). $\triangle DEF$ is a right triangle, so by Theorem $\PageIndex{1}$, $f^2 = d^2 + e^2$. We have $f^2 = d^2 + e^2 = a^2 + b^2 = c^2$ and therefore $f = c$. Therefore $\triangle ABC \cong \triangle DEF$ because $SSS = SSS$. Therefore, $\angle C + \angle F = 90^{\circ}$.

Figure $\PageIndex{4}$: Given $\triangle ABC$, draw $\triangle DEF$ so that $\angle F = 90^{\circ}$, $d = a$ and $e = b$.

Example $\PageIndex{5}$

Is $\triangle ABC$ a right triangle?

Solution

$\text{AC}^2 = 7^2 = 49$

$\text{BC}^2 = 9^2 = 81$

$\text{AB}^2 = (\sqrt{130})^2 = 130$

$49 + 81 = 130$.

so by Theorem $\PageIndex{2}$, $\triangle ABC$ is a right triangle.

Answer: yes.

Example $\PageIndex{6}$

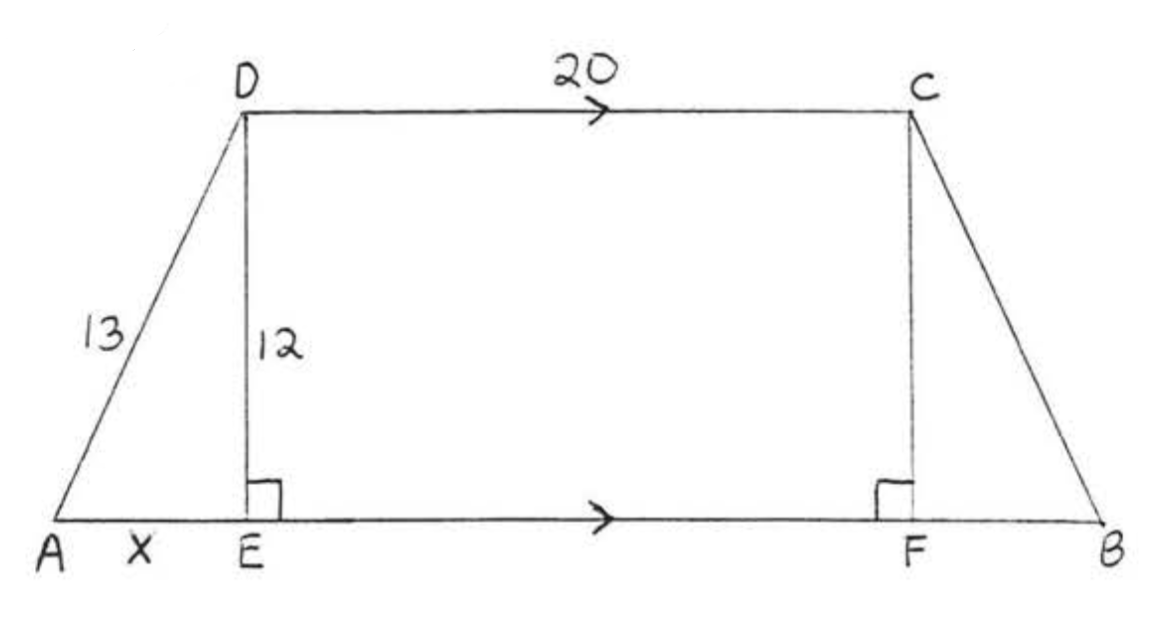
Find $x$ and $AB$:

Solution

$\begin{array} {rcl} {x^2 + 12^2} & = & {13^2} \\ {x^2 + 144} & = & {169} \\ {x^2} & = & {169 - 144} \\ {x^2} & = & {25} \\ {x} & = & {5} \end{array}$

$CDEF$ is a rectangle so $EF = CD = 20$ and $CF = DE = 12$. Therefore $FB = 5$ and $AB = AE + EF + FB = 5 + 20 + 5 = 30$.

Answer: $x = 5$, $AB = 30$.

Example $\PageIndex{7}$

Find $x$, $AC$ and $BD$:

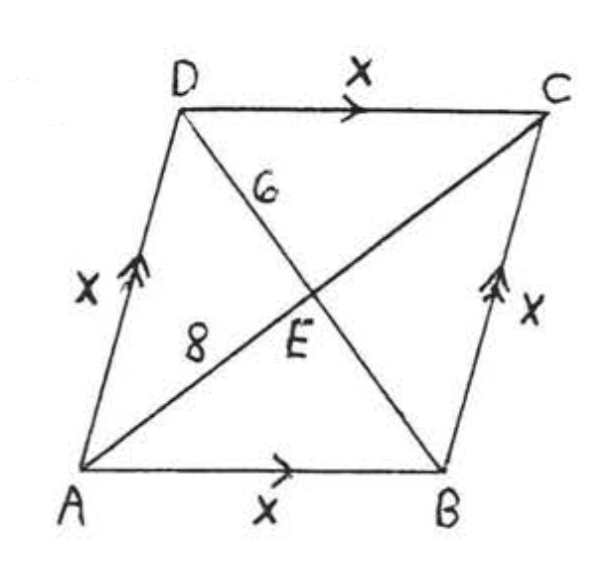
Solution

$ABCD$ is a rhombus. The diagonals of a rhombus are perpendicular and bisect each other.

$\begin{array} {rcl} {6^2 + 8^2} & = & {x^2} \\ {36 + 64} & = & {x^2} \\ {100} & = & {x^2} \\ {10} & = & {x} \end{array}$

$AC = 8 + 8 = 16, BD = 6 + 6 = 12.$

Answer: $x = 10, AC = 16, BD = 12$.

Example $\PageIndex{8}$

A ladder 39 feet long leans against a building, How far up the side of the building does the ladder reach if the foot of the ladder is 15 feet from the building?

Solution

$\begin{array} {rcl} {\text{leg}^2 + \text{leg}^2} & = & {\text{hyp}^2} \\ {x^2 + 15^2} & = & {39^2} \\ {x^2 + 225} & = & {1521} \\ {x^2} & = & {1521 - 225} \\ {x^2} & = & {1296} \\ {x} & = & {\sqrt{1296} = 36} \end{array}$

Answer: 36 feet.

Historical Note

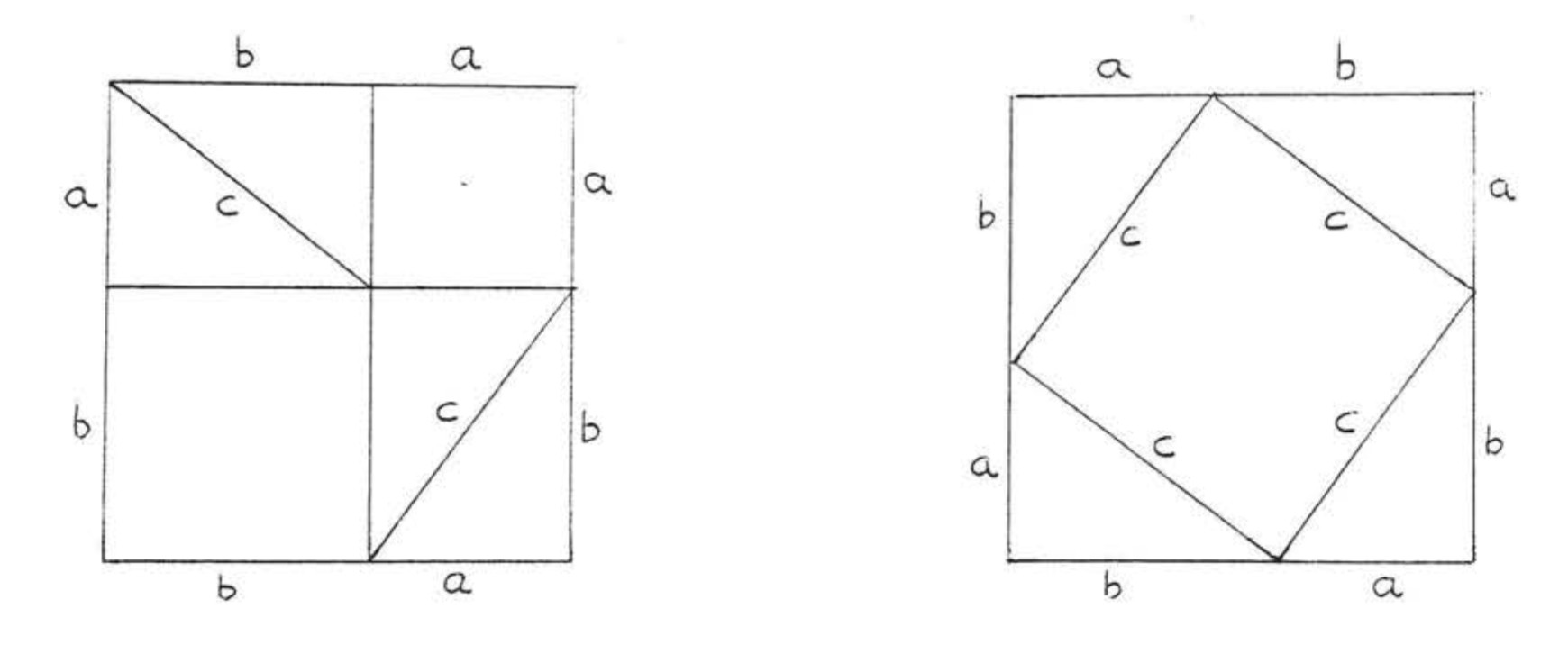
Pythagoras (c. 582 - 507 B.C.) was not the first to discover the theorem which bears his name. It was known long before his time by the Chinese, the Babylonians, and perhaps also the Egyptians and the Hindus, According to tradition, Pythagoras was the first to give a nroof of the theorem, His proof probably made use of areas, like the one suggested. In Figure $\PageIndex{5}$ below, (each square contains four congruent right triangles with sides of lengths $a$, $b$, and $c$, In addition the square on the left contains a square with side a and a square with side $b$ while the one on the right contains a square with side c.)

Figure $\PageIndex{5}$: Pythagoras may have proved $a^2 + b^2 = c^2$ in this way.

Since the time of Pythagoras, at least several hundred different proofs of the Pythagorean Theorem have been proposed, Pythagoras was the founder of the Pythagorean school, a secret religious society devoted to the study of philosophy, mathematics, and science. Its membership was a select group, which tended to keep the discoveries and practices of the society secret from outsiders. The Pythagoreans believed that numbers were the ultimate components of the universe and that all physical relationships could be expressed with whole numbers, This belief was prompted in part by their discovery that the notes of the musical scale were related by numerical ratios. The Pythagoreans made important contributions to medicine, physics, and astronomy, In geometry, they are credited with the angle s

um theorem for triangles, the properties of parallel lines, and the theory of similar triangles and proportions.

Problems

1 - 10. Find $x$. Leave answers in simplest radical form.

1.

2.

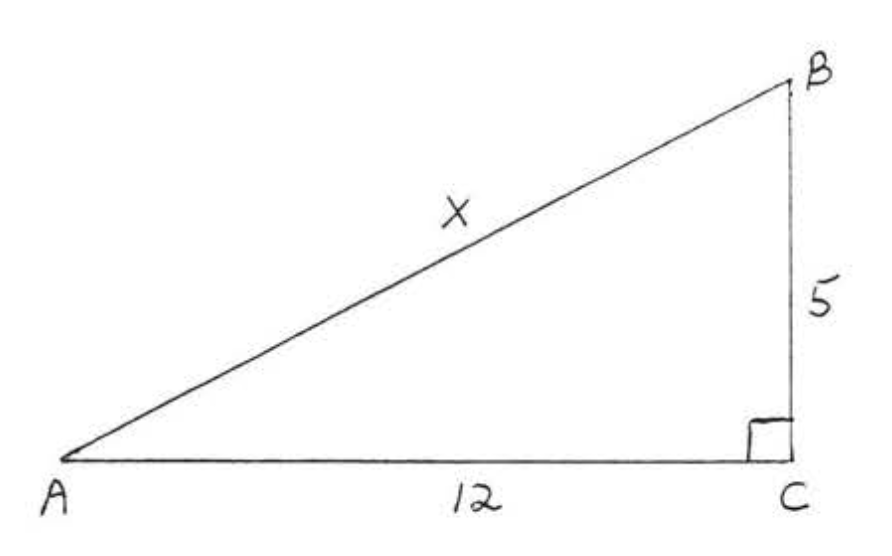
3.

4.

5.

6.

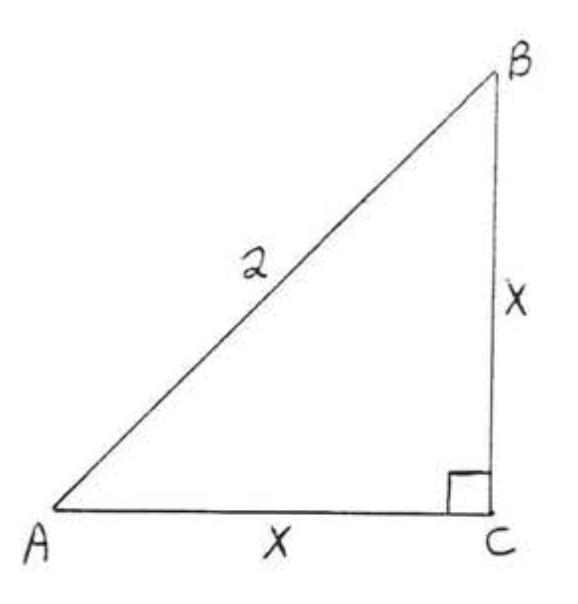
7.

8.

9.

10.

11 - 14. Find $x$ and all sides of the triangle:

11.

12.

13.

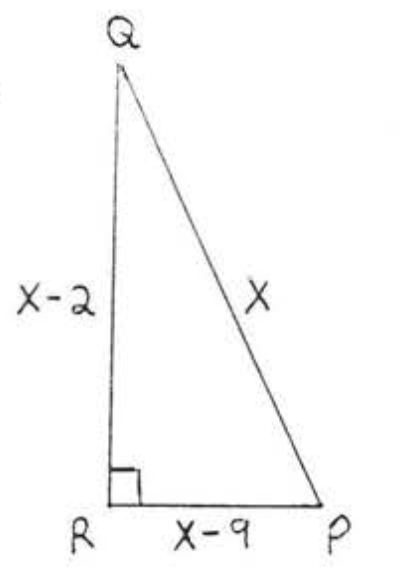
14.

15 - 16. Find $x$:

15.

16.

17. Find $x$ and $AB$.

18. Find $x$:

19. Find $x, AC$ and $BD$:

20. Find $x, AC$ and $BD$:

21. Find $x$ and $y$:

22. Find $x$, $AC$ and $BD$:

23. Find $x, AB$ and $BD$:

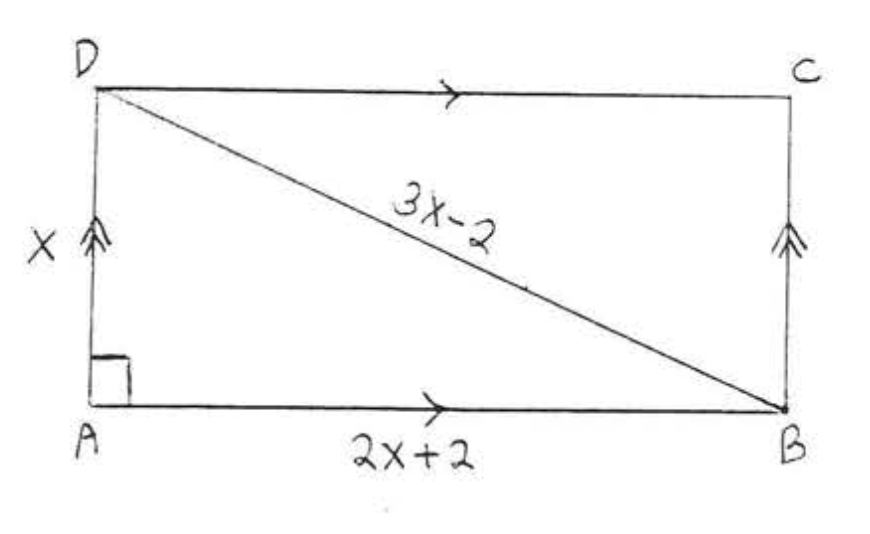
24. Find $x, AB$ and $AD$:

25 - 30. Is $\triangle ABC$ a right triangle?

25.

26.

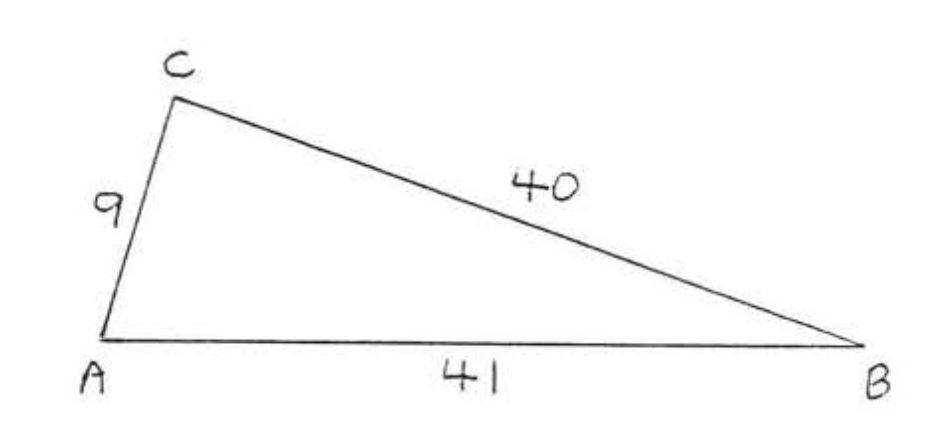
27.

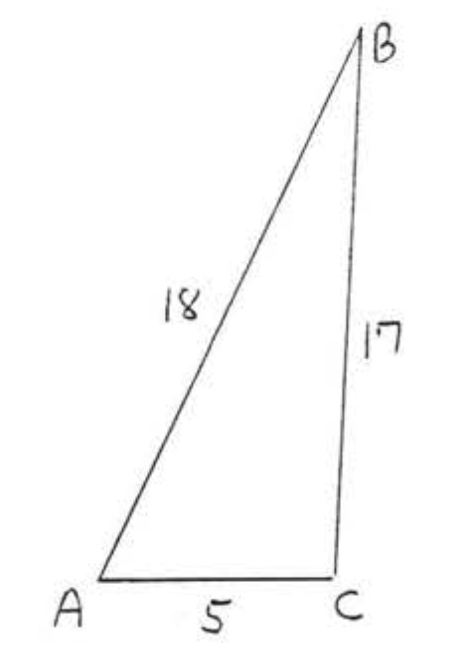
28.

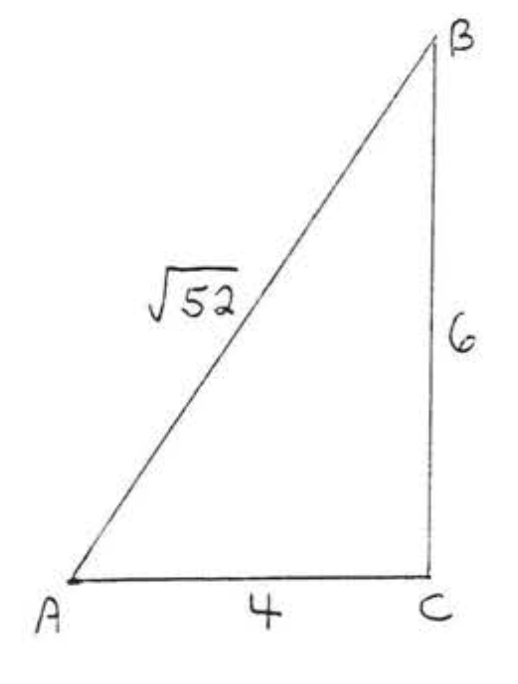
29.

30.

31. A ladder 25 feet long leans against a building, How far up the side of the building does the ladder reach if the foot of the ladder is 7 feet from the building?

32. A man travels 24 miles east and then 10 miles north. At the end of his journey how far is he from his starting point?

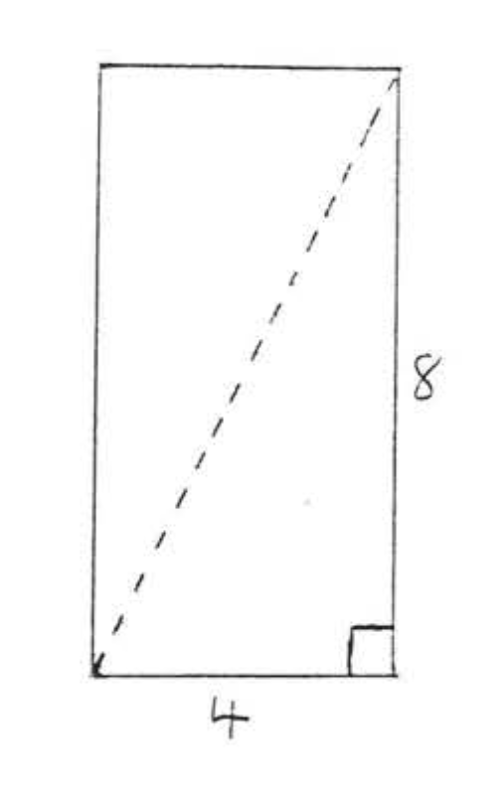
33. Can a table 9 feet wide (with its legs folded) fit through a rectangular doorway 4 feet by 8 feet?

34. A baseball diamond is a square 90 feet on each side, Find the distance from home plate to second base (leave answer in simplest radical form).