4.5: Спеціальні правильні трикутники

Існує два види прямокутного трикутника, які заслуговують на особливу увагу:$30^{\circ}-60^{\circ}-90^{\circ}$ прямокутний трикутник і прямокутний трикутник.$45^{\circ}-45^{\circ}-90^{\circ}$

30° -60° −90° Прямі трикутники

Трикутник, кути якого$90^{\circ}$ є$30^{\circ}, 60^{\circ},$ і називається$30^{\circ}-60^{\circ}-90^{\circ}$ трикутником. $\triangle ABC$на малюнку$\PageIndex{1}$ -$30^{\circ}-60^{\circ}-90^{\circ}$ трикутник зі стороною$AC=1$.

Малюнок$\PageIndex{1}$:$30^{\circ}-60^{\circ}-90^{\circ}$ Трикутник.

Малюнок$\PageIndex{2}$: Малюємо$BD$ і$CD$.

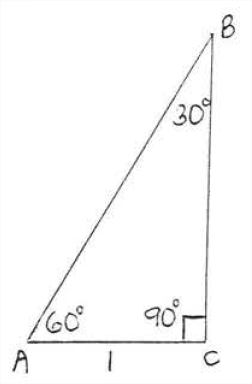
Щоб дізнатися більше про цей трикутник, намалюємо лінії$BD$ і$CD$ як на малюнку$\PageIndex{2}$. $\triangle ABC \cong \triangle DBC$by$ASA = ASA$ so$AC = DC = 1.$$\triangle ABD$ є рівнокутний трикутник, тому всі сторони повинні бути рівні$2.$. Тому$AB=2$ (рис.$\PageIndex{3}$).

Малюнок$\PageIndex{3}$:$\triangle ABD$ рівнокутна з усіма сторонами, рівними 2.

Нехай$x = BC$. Давайте знайдемо$x$. Застосовуючи теорему Піфагора до$\triangle ABC$,

$\begin{array} {rcl} {\text{leg}^2 + \text{leg}^2} & = & {\text{hyp}^2} \\ {1^2 + x^2} & = & {x^2} \\ {1 + x^2} & = & {4} \\ {x^2} & = & {3} \\ {x} & = & {\sqrt{3}} \end{array}$

Тепер припустимо, нам дано ще один$30^{\circ}-60^{\circ}-90^{\circ}$ трикутник$\triangle DEF$, зі стороною$DF = 8$ (рис.$\PageIndex{4}$). $\triangle DEF$схожий$\triangle ABC$ на малюнок$\PageIndex{3}$ Тому

$\begin{array} {rcl} {\dfrac{DF}{AC}} & = & {\dfrac{DE}{AB}} \\ {\dfrac{8}{1}} & = & {\dfrac{DE}{2}} \\ {16} & = & {DE} \end{array}$і$\begin{array} {rcl} {\dfrac{DF}{AC}} & = & {\dfrac{EF}{BC}} \\ {\dfrac{8}{1}} & = & {\dfrac{EF}{\sqrt{3}}} \\ {8\sqrt{3}} & = & {EF} \end{array}$

Малюнок$\PageIndex{3}$:

Наші висновки про трикутники$ABC$ і$DEF$ припускають наступну теорему:

Теорема$\PageIndex{1}$

У$30^{\circ} -60^{\circ}-90^{\circ}$ трикутнику гіпотенуза завжди вдвічі більша за катет, протилежний$30^{\circ}$ куту (коротший катет). Нога, протилежна$60^{\circ}$ куту (довша нога) завжди дорівнює коротшому часу ноги$\sqrt{3}$.

Малюнок$\PageIndex{5}$: Гіпотенуза вдвічі коротший катет, а довший катет дорівнює коротшому катету разів більше$\sqrt{3}$.

На малюнку$\PageIndex{5}$$s =$ коротший катет,$L =$ довший катет, а гіп = гіпотенуза. Теорема$\PageIndex{1}$ говорить, що

$$\boxed{ \begin{align*} \text{hyp} &= 2s \\[4pt] L &= s\sqrt{3} \end{align*}}$$

Зверніть увагу, що довша нога завжди нога протилежна (найвіддаленіша від)$60^{\circ}$ кута, а коротша нога завжди нога протилежна (найвіддаленіша від)$30^{\circ}$ кута.

Приклад$\PageIndex{1}$

Знайти$x$ і$y$:

Рішення

$\angle B = 180^{\circ} - (60^{\circ} + 90^{\circ}) = 180^{\circ} - 150^{\circ} = 30^{\circ}$, Так$\triangle ABC$ і$30^{\circ} - 60^{\circ} - 90^{\circ}$ трикутник. За$\PageIndex{1}$ теоремою

$\begin{array} {rcl} {\text{hyp}} & = & {2s} \\ {y} & = & {2(7) = 14.} \end{array}$$\begin{array} {rcl} {L} & = & {s\sqrt{3}} \\ {x} & = & {7\sqrt{3}} \end{array}$

Відповідь

$x = 7\sqrt{3}$,$y = 14$.

Приклад$\PageIndex{2}$

Знайти$x$ і$y$:

Рішення

$\angle B = 60^{\circ}$так$\triangle ABC$ це$30^{\circ} - 60^{\circ}-90^{\circ}$ трикутник. За$\PageIndex{1}$ теоремою

$\begin{array} {rcl} {L} & = & {s\sqrt{3}} \\ {10} & = & {x\sqrt{3}} \\ {\dfrac{10}{\sqrt{3}}} & = & {\dfrac{x\cancel{\sqrt{3}}}{\cancel{\sqrt{3}}}} \\ {x} & = & {\dfrac{10}{\sqrt{3}} = \dfrac{10}{\sqrt{3}} \cdot \dfrac{\sqrt{3}}{\sqrt{3}} = \dfrac{10\sqrt{3}}{3}.} \\ {\text{hyp}} & = & {2s} \\ {y} & = & {2x = 2(\dfrac{10\sqrt{3}}{3}) = \dfrac{20\sqrt{3}}{3}} \end{array}$

Відповідь

$x = \dfrac{10\sqrt{3}}{3}, y = \dfrac{20\sqrt{3}}{3}$.

45° -45° −90° Прямі трикутники

Другий особливий трикутник, який ми розглянемо, - це$45^{\circ}-45^{\circ} -90^{\circ}$ трикутник. Трикутник, кути якого є$45^{\circ}$$45^{\circ}$, і$90^{\circ}$ називається$45^{\circ}-45^{\circ} -90^{\circ}$ трикутником або рівнобедреним прямокутним трикутником. $\triangle ABC$на малюнку$\PageIndex{6}$ -$45^{\circ}-45^{\circ} -90^{\circ}$ трикутник зі стороною$AC = 1$.

Малюнок$\PageIndex{6}$:$45^{\circ}-45^{\circ} -90^{\circ}$ Трикутник.

Так як$\angle A = \angle B = 45^{\circ}$, сторони, протилежні цим кутам, повинні бути рівними (Теорема 2.5.2, Розділ 2.5). Тому$AC = BC = 1$.

Малюнок$\PageIndex{7}$: Ніжки$45^{\circ}-45^{\circ} -90^{\circ}$ трикутника рівні.

Нехай$x = AB$ (рис.$\PageIndex{7}$). За теоремою Піфагора

$\begin{array} {rcl} {\text{leg}^2 + \text{leg}^2} & = & {\text{hyp}^2} \\ {1^2 + 1^2} & = & {x^2} \\ {1 + 1} & = & {x^2} \\ {2} & = & {x^2} \\ {\sqrt{2}} & = & {x} \end{array}$

Приклад$\PageIndex{3}$

Знайти$x$:

Рішення

$\angle B = 180^{\circ} - (45^{\circ} + 90^{\circ}) = 180^{\circ} - 135^{\circ} = 45^{\circ}$. Так$\triangle ABC$ і$45^{\circ}-45^{\circ} -90^{\circ}$ трикутник. $AC = BC = 8$тому що ці сторони протилежні рівні кути. За теоремою Піфагора

$\begin{array} {rcl} {\text{leg}^2 + \text{leg}^2} & = & {\text{hyp}^2} \\ {8^2 + 8^2} & = & {x^2} \\ {64 + 64} & = & {x^2} \\ {128} & = & {x^2} \\ {x} & = & {\sqrt{128} = \sqrt{64} \sqrt{2} = 8 \sqrt{2}} \end{array}$

Відповідь

$x = 8\sqrt{2}$.

Трикутники фігури$\PageIndex{6}$ та приклад$\PageIndex{3}$ припускають наступну теорему:

Теорема$\PageIndex{2}$

У$45^{\circ}-45^{\circ} -90^{\circ}$ трикутнику катети рівні, а гіпотенуза дорівнює будь-якому разу катета$\sqrt{2}$.

На малюнку$\PageIndex{8}$,$\text{hyp}$ є гіпотенузою і$L$ є довжиною кожного катета. Теорема$\PageIndex{2}$ говорить, що

$$\boxed{ \text{hyp} = \sqrt{2} L }$$

Малюнок$\PageIndex{8}$: Ніжки рівні, а гіпотенуза дорівнює будь-якому часу катета$\sqrt{2}$.

Приклад$\PageIndex{4}$

Знайти$x$ і$y$:

Рішення

$\angle B = 45^{\circ}$. Так виглядає$\triangle ABC$ рівнобедрений прямокутний трикутник і$x = y$.

$\begin{array} {rcl} {x^2 + y^2} & = & {4^2} \\ {x^2 + x^2} & = & {16} \\ {2x^2} & = & {16} \\ {x^2} & = & {8} \\ {x} & = & {\sqrt{8} = \sqrt{4} \sqrt{2} = 2\sqrt{2}} \end{array}$

Відповідь:$x = y = 2 \sqrt{2}$.

Ще один метод:

$\triangle ABC$являє собою$45^{\circ}-45^{\circ} -90^{\circ}$ трикутник. Отже, за теоремою$\PageIndex{2}$,

$\begin{array} {rcl} {\text{hyp}} & = & {L\sqrt{2}} \\ {4} & = & {x\sqrt{2}} \\ {\dfrac{4}{\sqrt{2}}} & = & {\dfrac{x\cancel{\sqrt{2}}}{\cancel{\sqrt{2}}}} \\ {x} & = & {\dfrac{4}{\sqrt{2}} = \dfrac{4}{\sqrt{2}} \cdot \dfrac{\sqrt{2}}{\sqrt{2}} = \dfrac{4\sqrt{2}}{2} = 2\sqrt{2}} \end{array}$

Відповідь

$x = y = 2\sqrt{2}$.

Приклад$\PageIndex{5}$

Знайти$AB$:

Рішення

$\triangle ADE$являє собою$45^{\circ}-45^{\circ}-90^{\circ}$ трикутник. Звідси

$\begin{array} {rcl} {\text{hyp}} & = & {L \sqrt{2}} \\ {10} & = & {x\sqrt{2}} \\ {\dfrac{10}{\sqrt{2}}} & = & {\dfrac{x\cancel{\sqrt{2}}}{\cancel{\sqrt{2}}}} \\ {x} & = & {\dfrac{10}{\sqrt{2}} = \dfrac{10}{\sqrt{2}} \cdot \dfrac{\sqrt{2}}{\sqrt{2}} = \dfrac{10\sqrt{2}}{2} = 5\sqrt{2}} \\ {AE = x} & = & {5\sqrt{2}} \end{array}$

Тепер проведіть$CF$ перпендикулярно до$AB$ (рис.$\PageIndex{9}$). $\angle B = 45^{\circ}$так як$ABCD$ є рівнобедреною трапецією (Теорема 3.2.4, розділ 3.2).

Малюнок$\PageIndex{9}$: Малюємо$CF$ перпендикулярно$AB$.

Так$\triangle BCF$$45^{\circ}-45^{\circ}-90^{\circ}$ трикутник конгруентний$\triangle ADE$ і тому$BF = 5 \sqrt{2}$. $CDEF$є прямокутником і тому$EF = 10$. У нас є$AB = AE + EF + FB = 5\sqrt{2} + 10 + 5\sqrt{2} = 10\sqrt{2} + 10$.

Відповідь

$AB = 10\sqrt{2} + 10$.

Приклад$\PageIndex{6}$

Знайти$AC$ і$BD$:

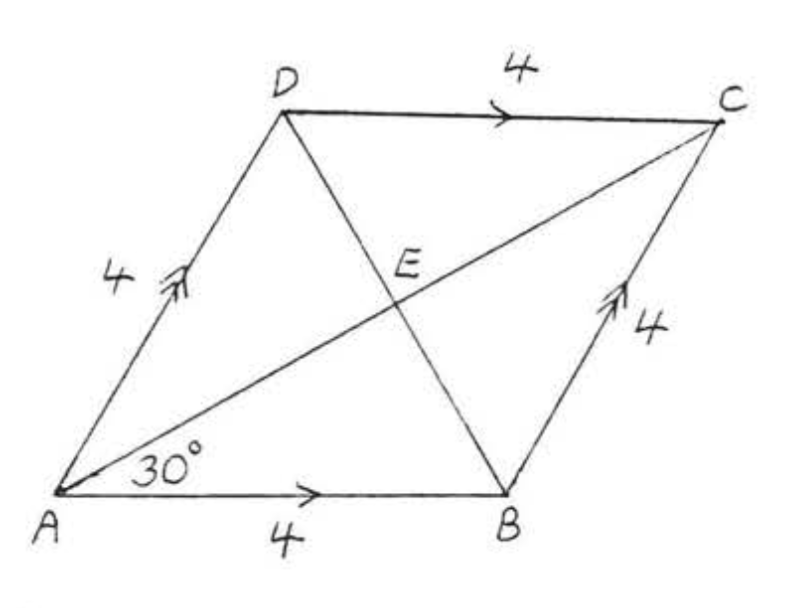
Рішення

$ABCD$це ромб. Діагоналі$AC$ і$BD$ перпендикулярні і бісекційні один одного. $\angle AEB = 90^{\circ}$і$\angle ABE = 180^{\circ} - (90^{\circ} - 30^{\circ}) = 60^{\circ}$. Так$\triangle AEB$ і$30^{\circ}-60^{\circ}-90^{\circ}$ трикутник.

$\begin{array} {rcl} {\text{hyp}} & = & {2s} \\ {4} & = & {2(BE)} \\ {2} & = & {BE} \\ {bd} & = & {2 + 2 = 4} \end{array}$$\begin{array} {rcl} {L} & = & {s\sqrt{3}} \\ {AE} & = & {2\sqrt{3}} \\ {AC} & = & {2\sqrt{3} + 2\sqrt{3}} \\ {AC} & = & {4\sqrt{3}} \end{array}$

Відповідь

$AC = 4\sqrt{3}, BD = 4$.

Історична примітка: Ірраціональні числа

Піфагорійці вважали, що всі фізичні відносини кораблів можуть бути виражені цілими числами. Однак сторони спеціальних трикутників, описаних в цьому розділі, пов'язані ірраціональними числами,$\sqrt{2}$ і$\sqrt{3}$. Ірраціональне число - це число, яке може бути наближеним, але не вираженим точно, співвідношенням цілих чисел. Наприклад,$\sqrt{2}$ може бути наближений з підвищенням точності такими співвідношеннями$1.4 = \frac{14}{10}$$1.41 = \frac{141}{100}$, як$1.414 = \frac{1414}{1000}$,, і т.д., але немає дробу цілих чисел, рівно рівному$\sqrt{2}$. (Більш детальну інформацію та докази див. у книзі Річардсона, переліченій у літературі). Піфагорійці виявили, що$\sqrt{2}$ було ірраціональним приблизно в V столітті до н.е., Це було величезним шоком для них, що не всі трикутники можна виміряти «точно». Можливо, вони навіть намагалися зберегти це відкриття в таємниці, побоюючись шкоди, яку вона завдасть їхній філософській достовірності.

Нездатність піфагорійців приймати ірраціональні числа мала сумні наслідки для розвитку математики. Пізніше грецькі математики уникали давати числові значення довжинам відрізків ліній. Задачі, алгебраїчні розв'язки яких можуть бути ірраціональними числами, наприклад, із квадратними рівняннями, були викладені та вирішені геометрично. Результатом стало те, що геометрія процвітала за рахунок алгебри. Індусам і арабам залишилося воскресити вивчення алгебри в середні віки. І лише в 19 столітті ірраціональні числа були поміщені в такі логічні рамки, які греки надали геометрії 2000 років тому.

Проблеми

1 - 10. Знайти$x$ і$y$:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11 - 14. Знайти$x$:

11.

12.

13.

14.

15 - 20. Знайти$x$ і$y$:

15.

16.

17.

18.

19.

20.

21 - 22. Знайти$x$ і$AB$:

21.

22.

23 - 24. Знайти$x$ і$y$:

23.

24.

25. Знайти$AC$ і$BD$:

26. Знайти$x, AC$ і$BD$: