9.6: Теорема Піфагора

Піфагор був грецьким математиком і філософом, народився на острові Самос (бл. 582 р. До н.е.). Він заснував ряд шкіл, одна, зокрема, в містечку на півдні Італії під назвою Кротоне, члени якого згодом стали називатися піфагорійцями. Близьке коло в школі, Математикоі, жив при школі, позбавляв себе від усіх особистих володінь, були вегетаріанцями, дотримувався суворої обітниці мовчання. Вони вивчали математику, філософію та музику, і вважали, що числа складають справжню природу речей, надаючи числам містичну або навіть духовну якість.

Сьогодні нічого не відомо про працях Піфагора, можливо, через секретність і мовчання піфагорійського суспільства. Однак одна з найвідоміших теорем у всій математиці носить його ім'я, теорема Піфагора.

ТЕОРЕМА ПІФАГОРА

Нехай c представляють довжину гіпотенузи, сторона прямокутного трикутника прямо навпроти прямого кута (прямий кут вимірює 90º) трикутника. Решта сторони прямокутного трикутника називаються ніжками прямокутного трикутника, довжини яких позначаються буквами а і б.

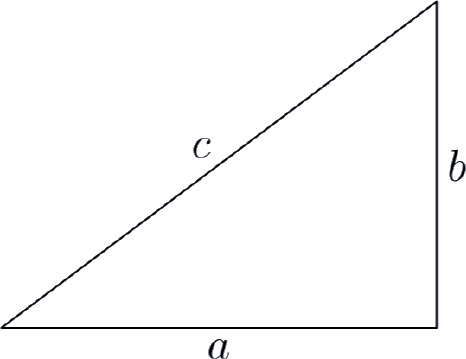
Співвідношення за участю катетів і гіпотенузи прямокутного трикутника, задане

$$a^2 + b^2 = c^2 \label{1}$$

називається теоремою Піфагора.

Зверніть увагу, що теорема Піфагора може бути застосована тільки до прямих трикутників. Давайте розглянемо просте застосування теореми Піфагора (Equat ion\ ref {1}).

Приклад$\PageIndex{2}$

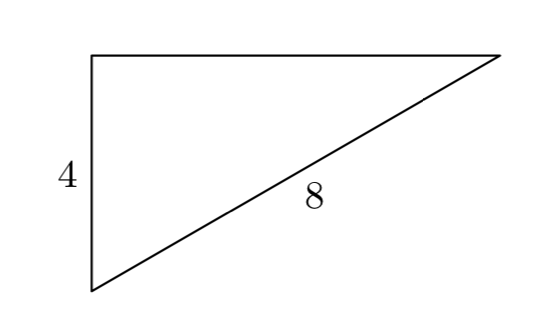
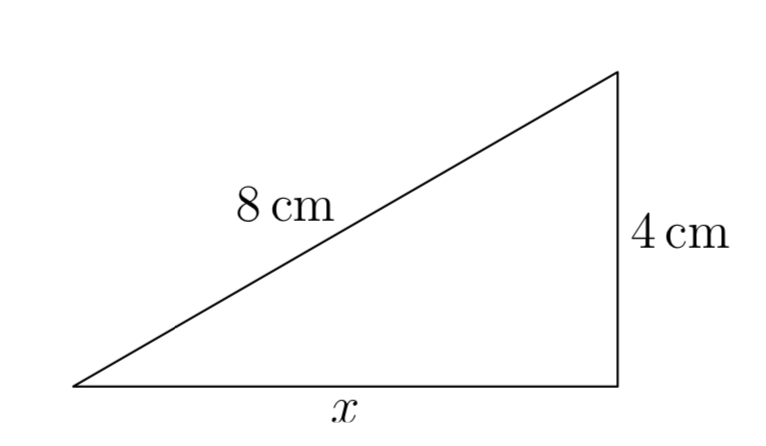
З огляду на, що довжина одного катета прямокутного трикутника становить 4 сантиметри, а гіпотенуза має довжину 8 сантиметрів, знайдіть довжину другого катета.

Почнемо з ескізу та маркування прямокутного трикутника заданою інформацією. Ми дозволимо х представляти довжину відсутньої ноги.

Малюнок 1. Ескіз робить все трохи простіше

Ось важлива порада.

ЧАЙОВІ$\PageIndex{3}$: Hypotenuse

Гіпотенуза - найдовша сторона прямокутного трикутника. Він розташований прямо навпроти прямого кута трикутника. Найголовніше, це величина, яка сама по собі ізольована в теоремі Піфагора (Equation\ ref {1}). Завжди ізолюйте величину, що представляє гіпотенузу з одного боку рівняння. «Ноги» йдуть на іншу сторону рівняння.

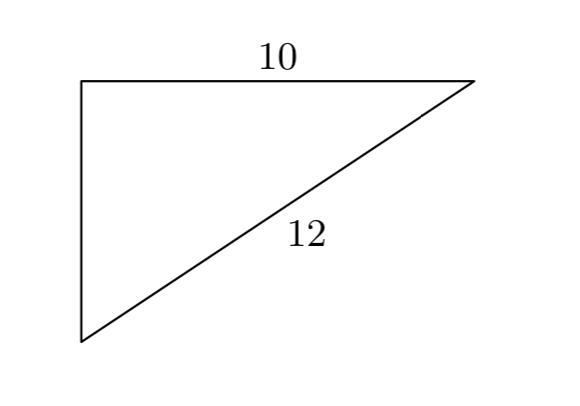
Отже, взявши кінчик до серця, і зазначивши довжини катетів і гіпотенузи на малюнку 1, пишемо

$4^2+x^2 = 8^2$.

Квадрат, потім ізолюйте x з одного боку рівняння.

$16+x^2 = 64$

$x^2 = 48$

Зазвичай ми б взяли плюс-мінус квадратний корінь при розв'язанні цього рівняння, але х являє собою довжину катета, яка повинна бути додатним числом. Отже, ми беремо тільки позитивний квадратний корінь 48.

$x = \sqrt{48}$

Звичайно, розмістіть свою відповідь в простій радикальній формі.

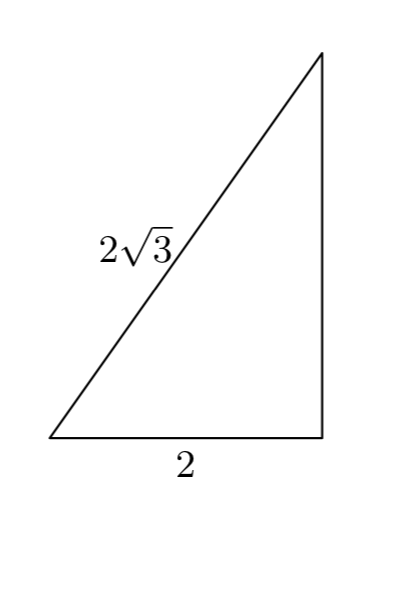
$x = \sqrt{16}\sqrt{3}$

$x = 4\sqrt{3}$

Якщо потрібно, ви можете скористатися графічним калькулятором, щоб наблизити цю довжину. До найближчої сотої частини сантиметра,$x \approx 6.93$ сантиметри.

Доказ теореми Піфагора

Невідомо, чи був Піфагор першим, хто надав доказ теореми Піфагора. Багато математичних істориків вважають, що ні. Дійсно, навіть невідомо, чи створив Піфагор доказ теореми, яка носить його ім'я, не кажучи вже про те, що першим надав доказ.

Є дані про те, що стародавні вавилоняни знали про теорему Піфагора за 1000 років до часу Піфагора. Глиняна табличка, яка зараз називається Плімптон 322 (див. Рис. 2), містить приклади Піфагорійських трійок, наборів трьох чисел, які задовольняють теоремі Піфагора (наприклад, 3, 4, 5).

Малюнок 2. Фотографія Плімптона 32.

Одне з найбільш ранніх записаних доказів теореми Піфагора датується династією Хань (206 р. До н.е. - 220 р. н.е.), і записаний в Chou Pei Suan Ching (див. Рис. Ви можете бачити, що ця цифра конкретно стосується випадку 3, 4, 5 прямокутного трикутника. Математичні історики поділяються щодо того, чи має зображення бути частиною загального доказу чи було просто розроблено для вирішення цього конкретного випадку. Існують також розбіжності щодо того, чи було доказ надано більш сучасним коментатором або датується далі в часі.

Малюнок 3. Фігура з Чоу Пей Суан Чінг

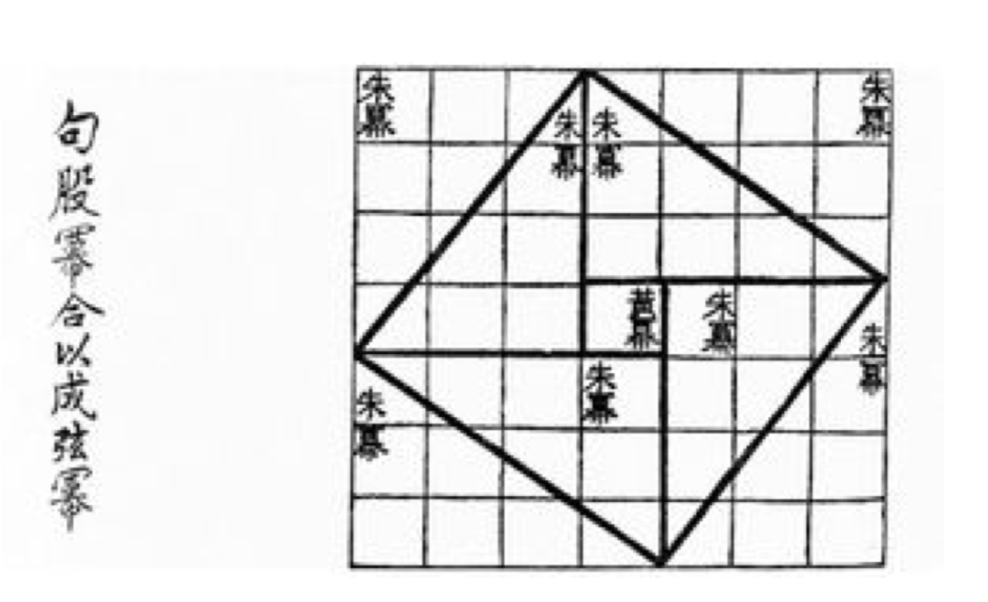
Однак Рисунок 3 пропонує шлях, який ми можемо взяти на шляху до доказу теореми Піфагора. Почніть з довільного прямокутного трикутника, що має катети довжин a і b, і гіпотенузи, що має довжину c, як показано на малюнку 4 (а).

Далі зробіть чотири копії трикутника, показаного на малюнку 4 (а), потім поверніть і перекладіть їх на місце, як показано на малюнку 4 (б). Зверніть увагу, що це утворює великий квадрат, який є c одиниць на стороні.

Далі положення трикутників на малюнку 4 (б) дозволяє утворювати менший, незаштрихований квадрат посередині більшого квадрата. Неважко обчислити довжину сторони цього меншого квадрата. Просто відніміть довжину меншої ноги від більшої ніжки вихідного трикутника. Таким чином, сторона меншого квадрата має довжину b − a.

Малюнок 4. Доказ теореми Піфагора.

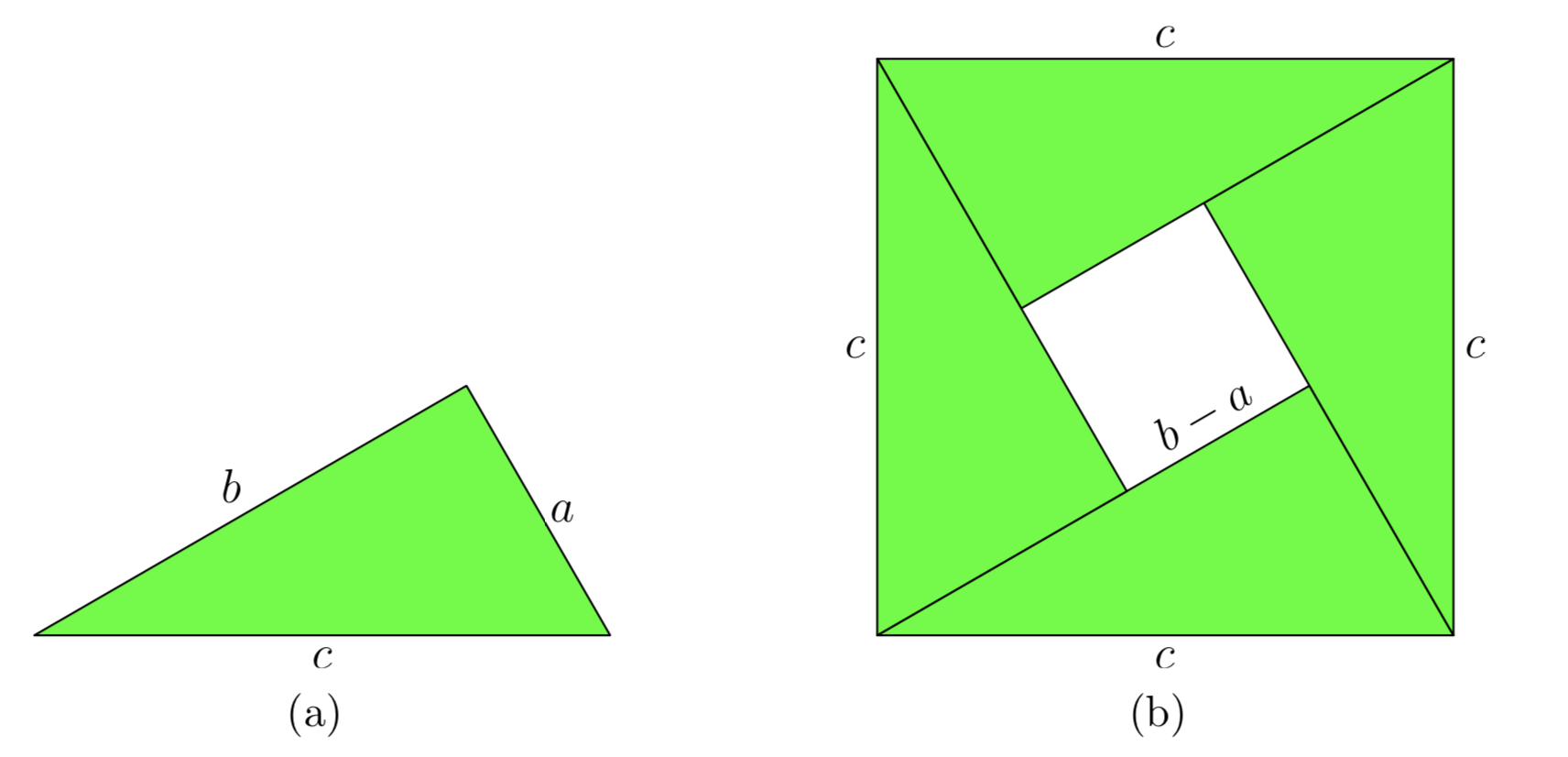
Тепер обчислимо площу великого квадрата на малюнку 4 (б) двома окремими способами.

• По-перше, великий квадрат на малюнку 4 (б) має сторону довжини c Тому площа великого квадрата дорівнює

  $Area = c^2$.

• По-друге, великий квадрат на малюнку 4 (b) складається з 4 трикутників однакового розміру і одного меншого квадрата, що має сторону довжини b−a. Ми можемо обчислити площу великого квадрата, підсумовуючи площу 4 трикутників і меншого квадрата.

1. Площа меншого квадрата дорівнює$(b−a)^2$.
2. Площа кожного трикутника дорівнює$\frac{ab}{2}$. Значить, площа чотирьох трикутників однакового розміру в чотири рази це число;

тобто,$4(\frac{ab}{2})$. Таким чином, площа великого квадрата дорівнює

Площа = Площа малого квадрата +$4 \cdot$ Площа трикутника

=$(b−a)^2+4(\frac{ab}{2})$.

Ми розрахували площу більшого квадрата двічі. Перший раз ми отримали$c^2$; вдруге ми отримали$(b−a)^2+4(\frac{ab}{2})$. Тому ці дві величини повинні бути рівними.

$c^2 = (b−a)^2+4(\frac{ab}{2})$.

Розгорніть біноміал і спростіть.

$c^2 = b^2−2ab+a^2 +2ab$

$c^2 = b^2+a^2$

Тобто,

$a^2+b^2 = c^2$,

і теорема Піфагора доведена.

Застосування теореми Піфагора

У цьому розділі ми розглянемо кілька застосувань теореми Піфагора, однієї з найбільш прикладних теорем у всій математиці. Просто запитайте свого місцевого тесляра.

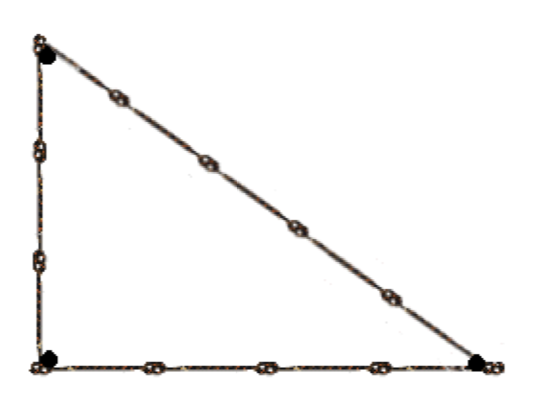
Стародавні єгиптяни брали б мотузку з 12 однаково розташованими вузлами, як показано на малюнку 5, і використовували її для квадратних кутів своїх будівель. Інструмент зіграв важливу роль у будівництві пірамід.

Малюнок 5. Базовий 3-4-5 прямокутний трикутник для квадратури кутів.

Теорема Піфагора також корисна в геодезії, картографії та навігації, щоб назвати кілька можливостей.

Давайте розглянемо кілька прикладів теореми Піфагора в дії.

Приклад$\PageIndex{4}$

Одна ніжка прямокутного трикутника на 7 метрів довша за іншу ногу. Довжина гіпотенузи становить 13 метрів. Знайдіть довжини всіх сторін прямокутного трикутника.

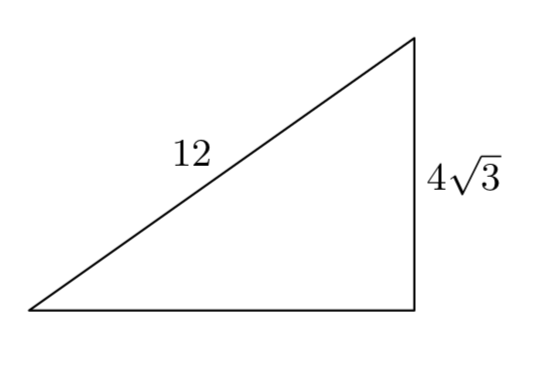
Нехай x представляють довжину одного катета прямокутного трикутника. Оскільки другий катет на 7 метрів довший за перший катет, довжина другого катета може бути представлена виразом x + 7, як показано на малюнку 6, де ми також позначили довжину гіпотенузи (13 метрів).

Малюнок 6. Друга нога на 7 метрів довша, ніж перша.

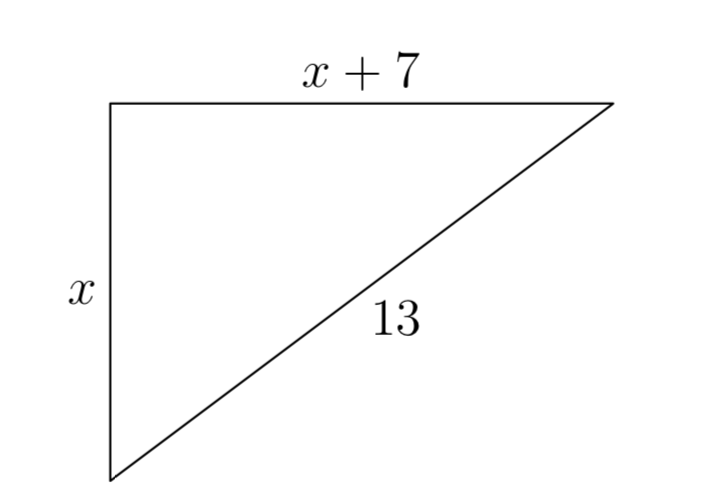
Не забудьте виділити довжину гіпотенузи з одного боку рівняння, що представляє теорему Піфагора. Тобто,

$x^2+(x+7)^2 = 13^2$.

Зверніть увагу, що катети йдуть з одного боку рівняння, гіпотенуза - з іншого. Квадратні і спростити. Не забудьте використовувати квадрат біноміального візерунка.

$x^2+x^2+14x+49 = 169$

$2x^2 +14x+49 = 169$

Це рівняння нелінійне, тому зробіть нуль з однієї сторони, віднімаючи 169 з обох сторін рівняння.

$2x^2+14x+49−169 = 0$

$2x^2 +14x−120 = 0$

Зверніть увагу, що кожен член з лівого боку рівняння ділиться на 2. Розділіть обидві сторони рівняння на 2.

$x^2+7x−60 = 0$

Скористаємося квадратичною формулою з a = 1, b = 7 і c = −60.

$x = \frac{−b \pm \sqrt{b^2−4ac}}{2a} = \frac{−7 \pm \sqrt{7^2 −4(1)(−60)}}{2(1)}$

Спростити.

$x = \frac{−7 \pm \sqrt{289}}{2}$

Зверніть увагу, що 289 - ідеальний квадрат ($17^2 = 289$). Таким чином,

$x = \frac{−7 \pm 17}{2}$.

Таким чином, у нас є два рішення,

х = 5 або х = −12.

Оскільки довжина повинна бути додатним числом, ми виключаємо − 12 з розгляду. Таким чином, довжина першої ноги дорівнює х = 5 метрів. Довжина другої ноги - х +7, або 12 метрів.

Перевірте. Перевірка - справа нескладна. Ніжки - 5 і 12 метрів відповідно, а гіпотенуза - 13 метрів. Зверніть увагу, що друга нога на 7 метрів довша, ніж перша. Крім того,

$5^2+12^2 = 25+144 = 169$,

який є квадратом 13.

Інтегральні сторони трикутника в попередньому прикладі, 5, 12 і 13, є прикладом піфагорійської трійки.

ПІФАГОРЕЙ ПОТРІЙНИЙ

Набір натуральних чисел a, b і c, називається Піфагорійською трійкою, якщо вони задовольняють теоремі Піфагора; тобто якщо

$a^2+b^2 = c^2$.

Якщо найбільший спільний коефіцієнт a, b і c дорівнює 1, то трійка (a, b, c) називається примітивною Піфагорійською трійкою.

Так, наприклад, Піфагорійська трійка (5, 12, 13) примітивна. Давайте розглянемо інший приклад.

Приклад$\PageIndex{5}$

Якщо (a, b, c) є піфагорійською трійкою, покажіть, що будь-який позитивний інтеграл кратний також є піфагорійською трійкою.

Таким чином, якщо натуральні числа (a, b, c) є піфагорійською трійкою, ми повинні показати, що (ka, kb, kc), де k - додатне число, також є піфагорійською трійкою.

Однак ми знаємо, що

$a^2+b^2 = c^2$.

Помножте обидві сторони цього рівняння на$k^2$.

$k^{2}a^2+k^{2}b^2 = k^{2}c^2$

Цей останній результат можна записати

$(ka)^2 + (kb)^2 = (kc)^2$.

Отже, (ka, kb, kc) є піфагорійською трійкою.

Отже, оскільки (3, 4, 5) є піфагорійською трійкою, ви можете подвоїти все, щоб отримати ще одну трійку (6, 8, 10). Зверніть увагу,$6^2 + 8^2 = 10^2$ що легко перевіряється. Аналогічно потроєння дає ще трійку (9 , 12, 15) і так далі.

У прикладі 5 ми показали, що (5, 12, 13) був потрійним, тому ми можемо взяти кратні для генерації інших Піфагорійських трійок, таких як (10, 24, 26) або (15, 36, 39), і так далі.

Формули для генерації піфагорійських трійок відомі ще з давніх-давен.

Приклад$\PageIndex{6}$

Наступна формула генерації Піфагорійських трійок була опублікована в Елементах Евкліда (325—265 до н.е.), одному з найуспішніших підручників в історії математики. Якщо m та n є додатними цілими числами з m > n, показати

$a = m^2−n^2$,

б = 2мн, (7)

$c = m^2+n^2$,

породжує Піфагора Трійки.

Нам потрібно лише показати, що формули для a, b і c задовольняють піфагора Тео рему. Маючи це розум, давайте спочатку обчислимо\(a^2+b^2\).

$a^2+b^2 = (m^2−n^2)^2+(2mn)^2$

=$m^4−2m^{2}n^{2}+n^4+4m^{2}n^2$

=$m^4+2m^{2}n^2+n^4$

З іншого боку,

$c^2 = (m^2+n^2)^2$

=$m^4+2m^{2}n^2+n^4$.
Звідси$a^2+b^2 = c^2$, і вирази для a, b і c утворюють піфагорійську трійку.

Як цікаво, так і весело генерувати Піфагорійські трійки за допомогою формул з Прикладу 6. Виберіть m = 4 і n = 2, потім

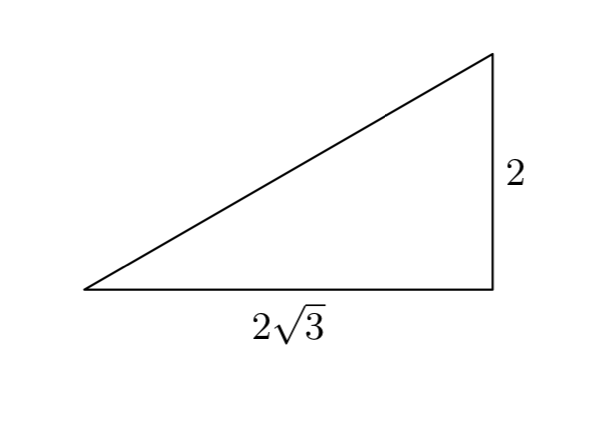
$a = m^2−n^2 = (4)^2−(2)^2 = 12$,

$b = 2mn = 2(4)(2) = 16$,

$c = m^2+n^2 =(4)^2+(2)^2 = 20$.

Легко перевірити, що потрійний (12, 16, 20) задовольнить$12^2+16^2 = 20^2$. Дійсно, зверніть увагу, що ця трійка кратна основній (3, 4, 5) трійці, тому вона також повинна бути Піфагорійською трійкою.

Також можна показати, що якщо m і n є відносно простими, і не обидва непарні або обидва парні, то формули в прикладі 6 генерують примітивний Піфагорейський Потрійний. Наприклад, вибираємо m = 5 і n = 2. Зауважте, що найбільший спільний дільник m = 5 і n = 2 дорівнює одиниці, тому m і n є відносно простими. Більш того, m непарна, а n - парна. Ці значення m і n генерують

$a = m^2−n^2 = (5)^2−(2)^2 = 21$,

$b = 2mn = 2(5)(2) = 20$,

$c = m^2+n^2 = (5)^2+(2)^2 = 29$.

Зверніть увагу, що

$21^2+20^2 = 441+400 = 841 = 29^2$.

Отже, (21, 20, 29) є піфагорійською трійкою. Причому найбільшим спільним дільником 21, 20 і 29 є один, тому (21, 20, 29) є примітивним.
Практичне застосування теореми Піфагора численні.

Приклад$\PageIndex{8}$

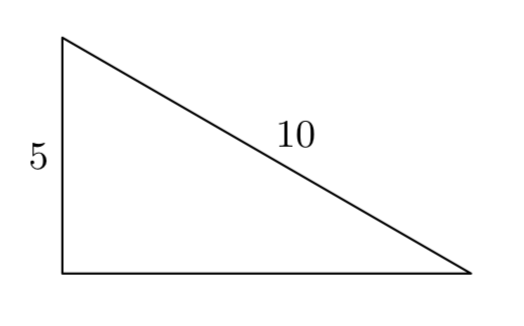
Художник притулює 20 футові сходи до стіни будинку. Підстава сходів знаходиться на рівній землі в 5 футах від стіни будинку. Наскільки високо вгору по стіні будинку буде досягати сходи?

Розглянемо трикутник на малюнку 7. Гіпотенуза трикутника являє собою сходи і має довжину 20 футів. Підстава трикутника являє собою відстань підстави сходів від стіни будинку і становить 5 футів в довжину. Вертикальна ніжка трикутника - це відстань, на яку сходи сягає вгору по стіні, і кількість, яку ми хочемо визначити.

Малюнок 7. Сходи спирається на стіну будинку.

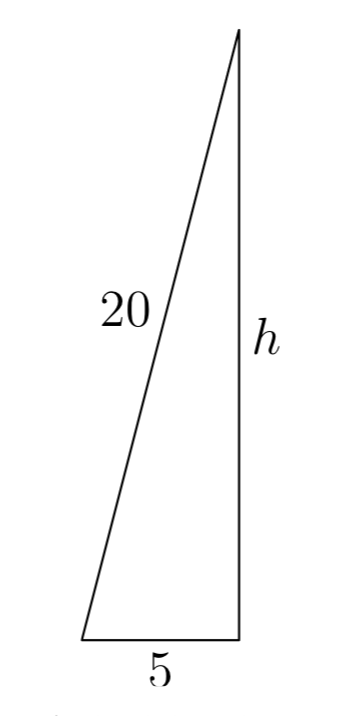
Застосовуючи теорему Піфагора,

$5^2+h^2 = 20^2$.

Знову зверніть увагу, що квадрат довжини гіпотенузи - це величина, яка ізольована на одній стороні рівняння.

Далі, квадрат, потім ізолюють термін, що містить h на одній стороні рівняння, віднімаючи 25 з обох сторін отриманого рівняння.

$25+h^2 = 400$

$h^2 = 375$

Нам потрібно лише витягти позитивний квадратний корінь.

$h = \sqrt{375}$

Ми могли б розмістити рішення в простій формі, тобто$h = 5\sqrt{15}$, але природа задачі вимагає десяткового наближення. За допомогою калькулятора і округлення до найближчої десятої частини фута,

$h \approx 19.4$.

Таким чином, сходи сягає приблизно 19,4 футів вгору по стіні.

Формула відстані

Нам часто потрібно обчислити відстань між двома точками P і Q в площині. Дійсно, це така часто повторювана потреба, ми хотіли б розробити формулу, яка дозволить швидко обчислити відстань між заданими точками P і Q. така формула є метою цього останнього розділу.

Нехай P (x1, y1) і Q (x2, y2) дві довільні точки в площині, як показано на малюнку 8 (а) і нехай d представляють відстань між двома точками.

Малюнок 8. Знаходження відстані між точками Р і Q.

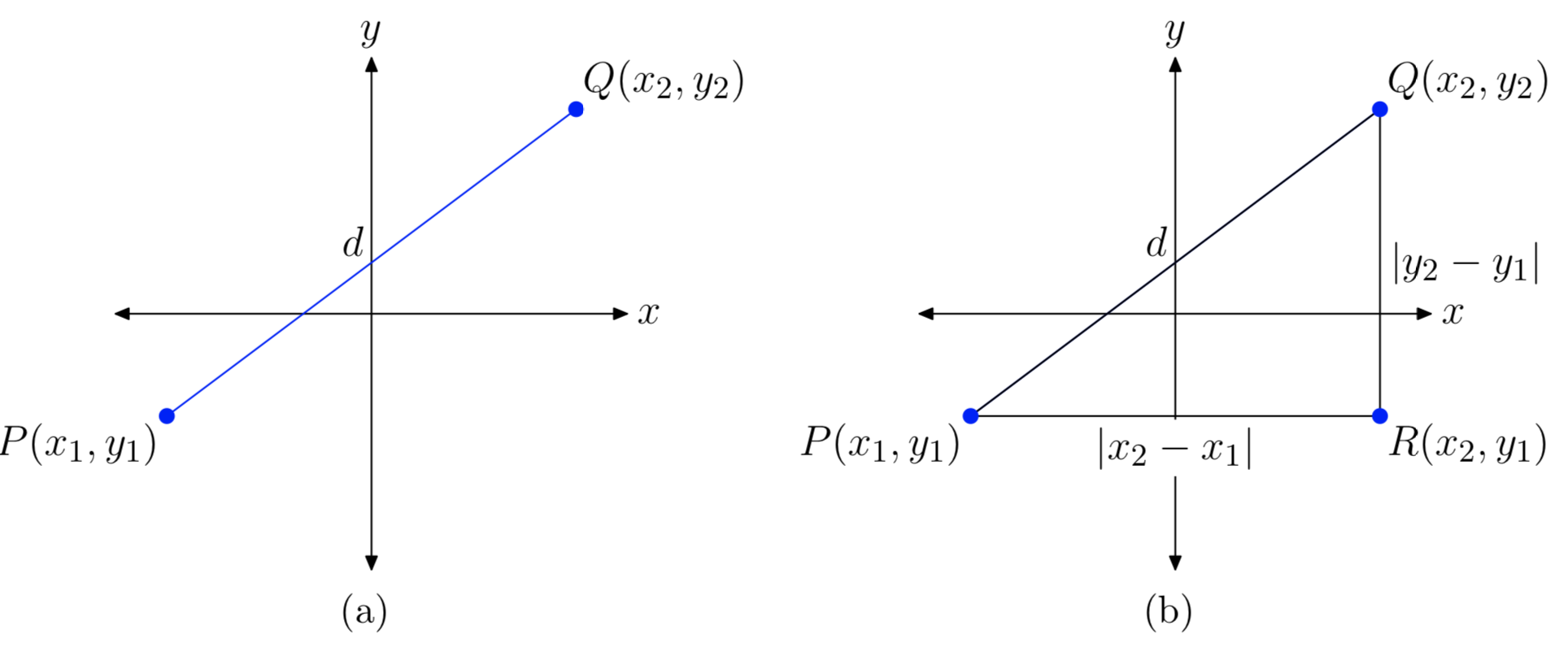
Щоб знайти відстань d, спочатку намалюйте прямокутний трикутник △ PQR, з ніжками, паралельними осям, як показано на малюнку 8 (б). Далі нам потрібно знайти довжини ніжок прямокутного трикутника △ PQR.

• Відстань між P і R знаходять шляхом віднімання координати x P з x-координати R і взяття абсолютного значення результату. Тобто відстань між P і R дорівнює$|x_{2}−x_{1}|$.
• Відстань між R і Q знаходять шляхом віднімання y-координати R з y-координати Q і взяття абсолютного значення результату. Тобто відстань між R і Q дорівнює$|y_{2}−y_{1}|$.

Тепер ми можемо використовувати теорему Піфагора для обчислення d. таким чином,

$d^2 = (|x_{2}−x_{1}|)^2+(|y_{2}−y_{1}|)^2$.

Однак для будь-якого дійсного числа a,

$(|a|)^2 = |a|·|a| = |a^2| = a^2$,

тому що a2 є невід'ємним. Значить,$(|x_{2} − x_{1}|)^2 = (x_{2} − x_{1})^2 and (|y_{2} − y_{1}|)^2 = (y_{2} − y_{1})^2$ і ми можемо написати

$d^2 = (x_{2}−x_{1})^2+(y_{2}−y_{1})^2$.

Прийняття позитивного квадратного кореня призводить до Формули відстані.

ФОРМУЛА ВІДСТАНІ

Нехай P (x1, y1) і Q (x2, y2) дві довільні точки на площині. Відстань d між точками P і Q задається за формулою

$d = \sqrt{(x_{2}−x_{1})^2+(y_{2}−y_{1})^2}$. (9)

Напрямок віднімання не має значення. Оскільки ви квадратуєте результат віднімання, ви отримуєте однакову відповідь незалежно від напрямку віднімання (наприклад,\((5 − 2)^2 = (2 − 5)^2\)). Thus, it doesn’t matter which point you designate as the точка P, а також не має значення, яку точку ви позначили як точку Q. Просто відніміть x - координати і квадрат, відніміть y -координати і квадрат, додайте, потім візьміть квадратний корінь.

Давайте розглянемо приклад.

Приклад$\PageIndex{10}$

Знайти відстань між точками P (−4, −2) та Q (4, 4).

Це допомагає інтуїція, якщо ми малюємо картинку, як ми маємо на малюнку 9. Тепер можна взяти компас і відкрити його на відстань між точками Р і Q. Потім ви можете розмістити компас на горизонтальній осі (або будь-якій горизонтальній лінії сітки), щоб оцінити відстань між точками P і Q. Ми зробили це на нашому графічному папері і оцінили відстань$d \approx 10$.

Малюнок 9. Графік відстані між P (−4, −2) та Q (4, 4).

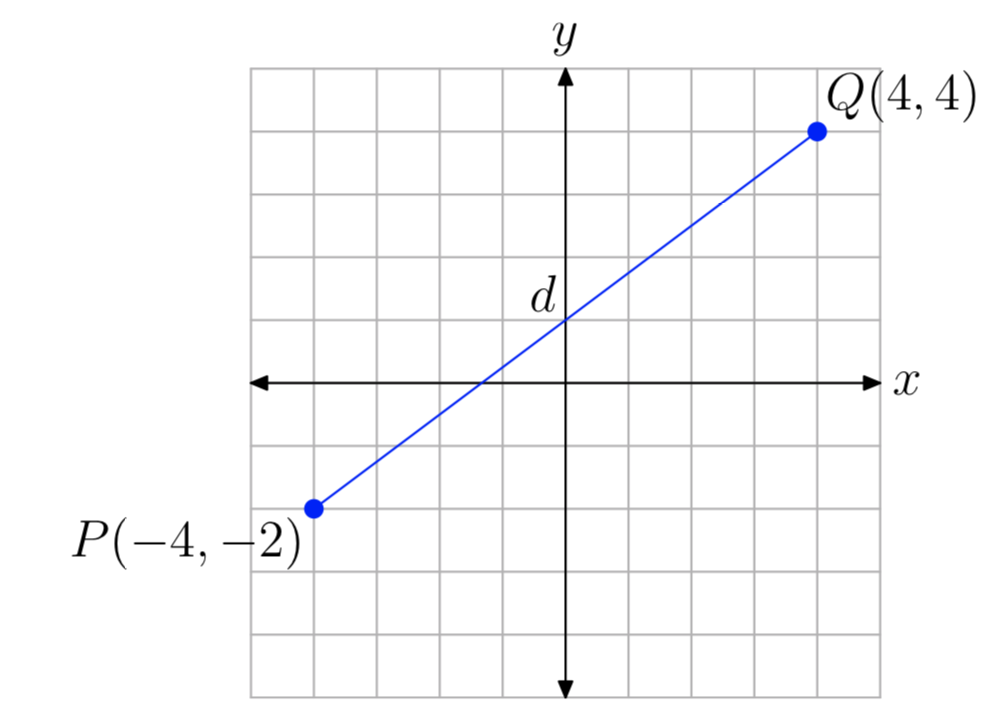
Давайте тепер скористаємося формулою відстані, щоб отримати точне значення відстані d. with$(x_{1}, y_{1})$ = P (−4, −2) і$(x_{2}, y_{2})$ = Q (4, 4),

$d = \sqrt{(x_{2}−x_{1})^2+(y_{2}−y_{1})^2}$

=$\sqrt{(4−(−4))^2+(4−(−2))^2}$

=$\sqrt{8^2+6^2}$

=$\sqrt{64+36}$

=$\sqrt{100}$

= 10.

Це не часто, що ваш точний результат узгоджується з вашим наближенням, тому ніколи не хвилюйтеся, якщо ви вимкнені лише трохи.

Вправа

У вправах 1 - 8 вкажіть, чи є дана трійка піфагорійською трійкою. Дайте привід для вашої відповіді.

Вправа$\PageIndex{1}$

(8, 15, 17)

Відповідь

Так, тому що$8^2 + 15^2 = 17^2$

Вправа$\PageIndex{2}$

(7, 24, 25)

Вправа$\PageIndex{3}$

(8, 9, 17)

Відповідь

Ні, тому що$8^2+9^2 \ne 17^2$

Вправа$\PageIndex{4}$

(4, 9, 13)

Вправа$\PageIndex{5}$

(12, 35, 37)

Відповідь

Так, тому що$12^2 + 35^2 = 37^2$

Вправа$\PageIndex{6}$

(12, 17, 29)

Вправа$\PageIndex{7}$

(11, 17, 28)

Відповідь

Ні, тому що$11^2 + 17^2 \ne 28^2$

Вправа$\PageIndex{8}$

(11, 60, 61)

У вправах 9 - 16 створіть рівняння для моделювання обмежень задачі та розв'язування. Використовуйте свою відповідь, щоб знайти відсутню сторону заданого прямокутного трикутника. Включіть ескіз з вашим рішенням і перевірте свій результат.

Вправа$\PageIndex{9}$

Відповідь

4

Вправа$\PageIndex{10}$

Вправа$\PageIndex{11}$

Відповідь

$4\sqrt{2}$

Вправа$\PageIndex{12}$

Вправа$\PageIndex{13}$

Відповідь

$2\sqrt{2}$

Вправа$\PageIndex{14}$

Вправа$\PageIndex{15}$

Відповідь

$5\sqrt{3}$

Вправа$\PageIndex{16}$

У Вправи 17 - 20 створіть рівняння, яке моделює обмеження задачі. Вирішіть рівняння і використовуйте результат, щоб відповісти на питання. Озирніться назад і перевірте свій результат.

Вправа$\PageIndex{17}$

Ніжки прямокутного трикутника є послідовними натуральними числами. Гіпотенуза має довжину 5. Які бувають довжини ніг?

Відповідь

Ноги мають довжину 3 і 4.

Вправа$\PageIndex{18}$

Ніжки прямокутного трикутника є послідовними парними цілими числами. Гіпотенуза має довжину 10. Які бувають довжини ніг?

Вправа$\PageIndex{19}$

Одна ніжка прямокутного трикутника на 1 сантиметр менше, ніж в два рази більше довжини першої ноги. Якщо довжина гіпотенузи дорівнює 17 сантиметрам, знайдіть довжини катетів.

Відповідь

Ноги мають довжину 8 і 15 сантиметрів.

Вправа$\PageIndex{20}$

Одна ніжка прямокутного трикутника на 3 фути довше, ніж в 3 рази більше довжини першої ноги. Довжина гіпотенузи становить 25 футів. Знайдіть довжини ніжок.

Вправа$\PageIndex{21}$

Піфагора приписують наступні формули, які можуть бути використані для генерації піфагорійських трійок.

а = м

$b = \frac{m^2−1}{2}$,

$c = \frac{m^2+1}{2}$

Скористайтеся технікою Прикладу 6, щоб продемонструвати, що наведені вище формули породжуватимуть трійки Піфагора, за умови, що m - непарне натуральне число більше одиниці. По-друге, згенерувати принаймні 3 екземпляри Піфагорійських трійок за формулою Піфагора.

Відповідь

(3, 4, 5), (5, 12, 13), і (7, 24, 25), при m = 3, 5 і 7 відповідно.

Вправа$\PageIndex{22}$

Платону (380 до н.е.) приписують наступні формули, які можуть бути використані для генерації піфагорійських трійок.

$a = 2m$

$b = m^2 − 1$,

$c = m^2 + 1$

Скористайтеся технікою Прикладу 6, щоб продемонструвати, що наведені вище формули породжуватимуть трійки Піфагора, за умови, що m є додатним цілим числом, більшим за 1. По-друге, згенерувати принаймні 3 екземпляри Піфагорійських трійок за формулою Платона.

У вправах 23 - 28 створіть рівняння, яке моделює обмеження задачі. Вирішіть рівняння і використовуйте результат для відповіді. Озирніться назад і перевірте свою відповідь.

Вправа$\PageIndex{23}$

Фріц і Грета висаджують прямокутний сад розміром 12 футів на 18 футів і викладають його за допомогою струни. Вони хотіли б знати довжину діагоналі, щоб переконатися, що утворюються прямі кути. Знайти довжину діагоналі. Приблизна ваша відповідь в межах 0.1 футів.

Відповідь

21. 63 футів

Вправа$\PageIndex{24}$

Ангеліна та Маркос висаджують прямокутний сад розміром 20 футів на 28 футів і викладають його за допомогою мотузки. Вони хотіли б знати довжину діагоналі, щоб переконатися, що утворюються прямі кути. Знайти довжину діагоналі. Приблизна ваша відповідь в межах 0.1 футів.

Вправа$\PageIndex{25}$

Основа 36-футового дроту для хлопця розташована на відстані 16 футів від основи телефонного стовпа, який він закріплює. Наскільки високо до полюса досягає дроти хлопця? Приблизна ваша відповідь в межах 0,1.

Відповідь

32. 25 футів

Вправа$\PageIndex{26}$

Основа дроту довжиною 35 футів розташована на відстані 10 футів від основи телефонного стовпа, який він закріплює. Наскільки високо до полюса досягає дроти хлопця? Приблизна ваша відповідь в межах 0.1 футів.

Вправа$\PageIndex{27}$

Стерео приймач знаходиться в кутку 13-футового на 16-футовий прямокутної кімнати. Провід динаміка буде проходити під килимом, по діагоналі, до динаміка в дальньому кутку. Якщо потрібно 3 фути провисання на кожному кінці, як довго слід придбати шматок дроту? Приблизна ваша відповідь в межах 0.1 футів.

Відповідь

26. 62 футів

Вправа$\PageIndex{28}$

Стереоприймач знаходиться в кутку прямокутної кімнати розміром 10 футів на 15 футів. Провід динаміка буде проходити під килимом, по діагоналі, до динаміка в дальньому кутку. Якщо потрібно 4 фути провисання на кожному кінці, як довго слід придбати шматок дроту? Приблизна ваша відповідь в межах 0.1 футів.

У вправах 29 - 38 використовуйте формулу відстані, щоб знайти точну відстань між заданими точками.

Вправа$\PageIndex{29}$

(−8, −9) та (6, −6)

Відповідь

$\sqrt{205}$

Вправа$\PageIndex{30}$

(1, 0) і (− 9, − 2)

Вправа$\PageIndex{31}$

(− 9, 1) і (− 8, 7)

Відповідь

$\sqrt{37}$

Вправа$\PageIndex{32}$

(0, 9) і (3, 1)

Вправа$\PageIndex{33}$

(6, −5) і (−9, −2)

Відповідь

$\sqrt{234} = 3\sqrt{26}$

Вправа$\PageIndex{34}$

(−5, 6) і (1, 4)

Вправа$\PageIndex{35}$

(−7, 7) і (−3, 6)

Відповідь

$\sqrt{17}$

Вправа$\PageIndex{36}$

(−7, −6) та (−2, −4)

Вправа$\PageIndex{37}$

(4, −3) і (−9, 6)

Відповідь

$\sqrt{250} = 5\sqrt{10}$

Вправа$\PageIndex{38}$

(−7, −1) та (4, −5)

У вправах 39 - 42 створіть рівняння, яке моделює обмеження задачі. Вирішіть рівняння і використовуйте результат, щоб відповісти на питання. Озирніться назад і перевірте свій результат.

Вправа$\PageIndex{39}$

Знайти k так, щоб точка (4, k) була$2\sqrt{2}$ одиницями, віддаленими від точки (2, 1).

Відповідь

k = 3, −1.

Вправа$\PageIndex{40}$

Знайти k так, щоб точка (k, 1) була$2\sqrt{2}$ одиницями від точки (0, −1)

Вправа$\PageIndex{41}$

Знайти k так, щоб точка (k, 1) була$\sqrt{17}$ одиницями від точки (2, −3)

Відповідь

k = 1, 3.

Вправа$\PageIndex{42}$

Знайти k так, щоб точка (−1, k) була$\sqrt{13}$ одиницями від точки (−4, −3).

Вправа$\PageIndex{43}$

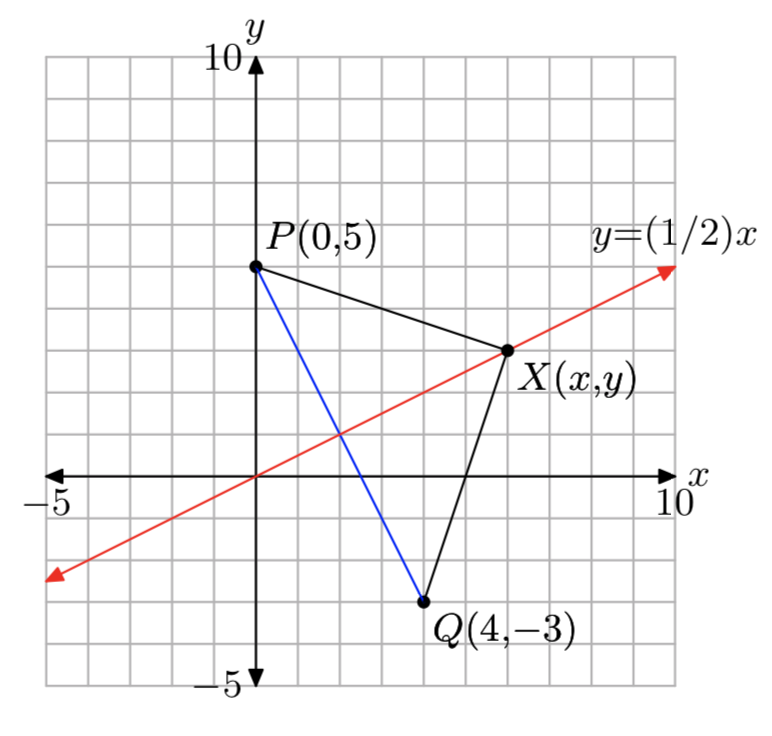
Налаштуйте систему координат на аркуші графічного паперу. Позначте та масштабуйте кожну вісь. Покладіть точки P (0, 5) та Q (4, −3) на вашій системі координат.

а) Побудуйте кілька точок, які знаходяться на рівній відстані від точок P і Q на вашій системі координат. Який графік ви отримаєте, якщо побудувати всі точки, які рівновіддалені від точок P і Q? Визначте рівняння графіка, вивчивши отримане зображення на вашій системі координат.

б) За допомогою формули відстані знайти рівняння графіка всіх точок, рівновіддалених від точок P і Q. підказка: Нехай (x, y) представляють довільну точку на графіку всіх точок, рівновіддалених від точок P і Q. обчисліть відстані від точки (x, y) до точок P і Q окремо, потім встановіть їх рівними і спростіть отримане рівняння. Зауважте, що цей аналітичний підхід повинен забезпечувати рівняння, яке відповідає рівнянню, знайденому графічним підходом у частині (а).

Відповідь

а) На наступному малюнку XP = XQ.

б)$y = \frac{1}{2}x$

Вправа$\PageIndex{44}$

Налаштуйте систему координат на аркуші графічного паперу. Позначте та масштабуйте кожну вісь. Покладіть точку P (0, 2) і позначте її координатами. Намалюйте лінію y = −2 і позначте її рівнянням.

а) Покладіть кілька точок, які знаходяться на рівній відстані від точки P і лінії y = −2 у вашій системі координат. Який графік ви отримаєте, якщо побудувати всі точки, що знаходяться на рівній відстані від точок P і лінії y = −2.

б) За допомогою формули відстані знайти рівняння графіка всіх точок, що знаходяться на рівновіддаленому від точок Р і лінії y = −2. Підказка: Нехай (x, y) представляють довільну точку на графіку всіх точок, рівновіддалених від точок P і лінії y = −2. Обчисліть відстані від точки (x, y) до точок P і лінії y = −2 окремо, після чого встановіть їх рівними і спростіть отримане рівняння.

Вправа$\PageIndex{45}$

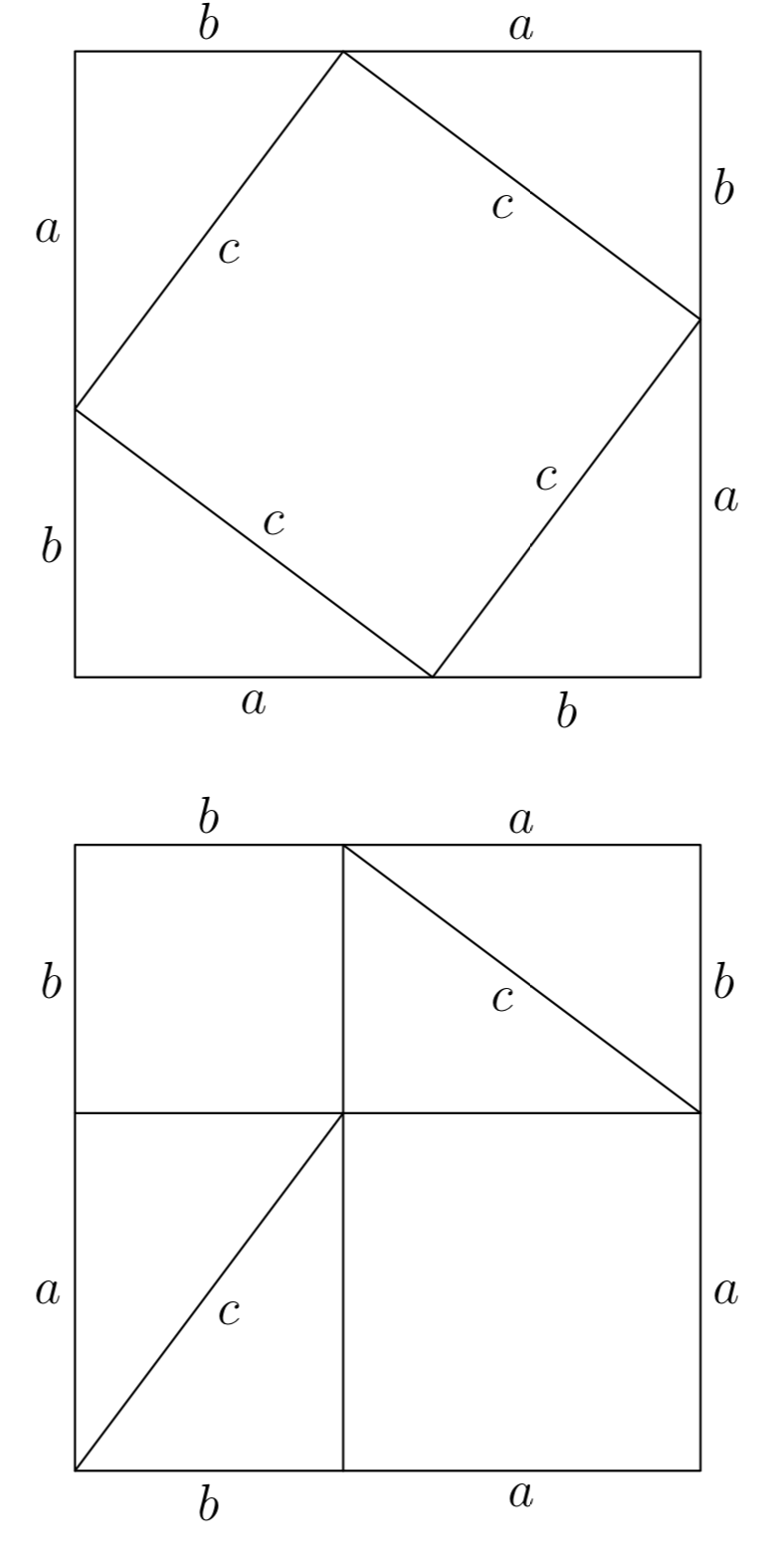
Скопіюйте наступний малюнок на аркуш графічного паперу. Відріжте шматочки першої фігурки ножицями, потім переставте їх, щоб сформувати другу фігуру. Поясніть, як це доводить теорема Піфагора.

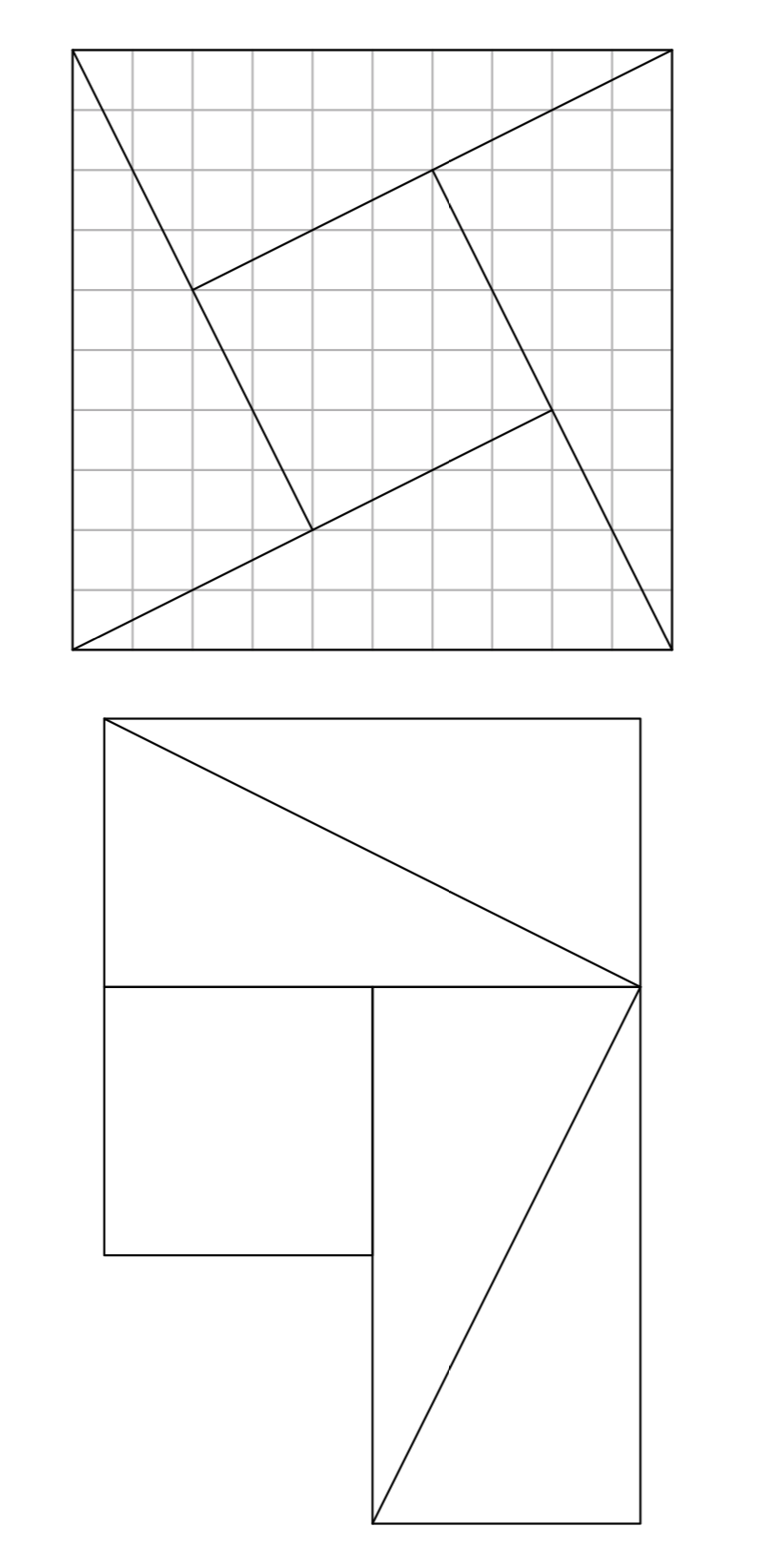
Вправа$\PageIndex{46}$

Порівняйте цей образ з наступним і поясніть, як це доводить теорема Піфагора.

​​​​​​​