4.2: Подібні трикутники
- Page ID
- 58841
Кажуть, що два трикутника схожі, якщо вони мають рівні набори кутів. На малюнку\(\PageIndex{1}\),\(\triangle ABC\) схожий\(\triangle DEF.\) на Кути, які рівні називаються відповідними кутами. На малюнку\(\angle A\)\(\angle B\) відповідає\(\PageIndex{1}\)\(\angle D\)\(\angle E\), відповідає і\(\angle C\) відповідає\(\angle F\). Сторони, що з'єднують відповідні вершини, називаються відповідними сторонами. На малюнку\(AB\)\(BC\) відповідає\(\PageIndex{1}\)\(DE\)\(EF\), відповідає і\(AC\) відповідає\(DF\). Символ подібного є\(\sim\). Оператор подібності завжди\(\triangle ABC \sim \triangle DEF\) буде записаний так, щоб відповідні вершини з'являлися в одному порядку.
Для трикутників на малюнку\(\PageIndex{1}\) ми також могли б написати\(\triangle BAC \sim \triangle BDF\) або,\(\triangle ACB \sim \triangle DFE\) але ніколи\(\triangle ABC \sim \triangle EDF\) ні\(\triangle ACB \sim \triangle DEF\).
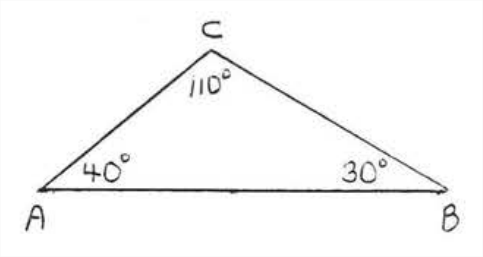

Ми можемо сказати, які сторони відповідають за твердженням подібності. Наприклад, якщо\(\triangle ABC \sim \triangle DEF\), то сторона\(AB\) відповідає стороні,\(DE\) тому що обидві є першими двома літерами. \(BC\)відповідає\(EF\) тому, що обидві є останніми двома літерами,\(AC\) відповідає\(DF\) тому, що обидві складаються з першої та останньої літер.
Визначте, чи схожі трикутники, і якщо так, напишіть заяву подібності:

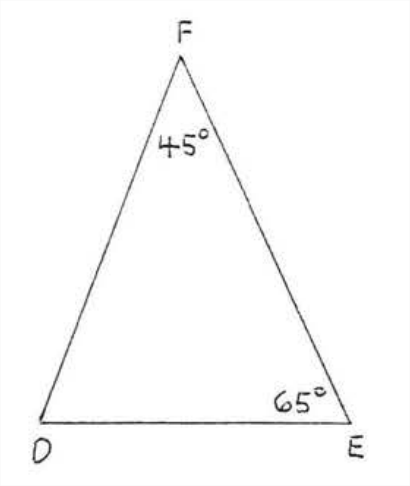
Рішення
\[\angle C = 180^{\circ} - (65^{\circ} + 45^{\circ}) = 180^{\circ} - 110^{\circ} = 70^{\circ} \nonumber\]
\[\angle D = 180^{\circ} - (65^{\circ} + 45^{\circ}) = 180^{\circ} - 110^{\circ} = 70^{\circ} \nonumber\]
Тому обидва трикутника мають однакові кути і\(\triangle ABC \sim \triangle EFD\).
Відповідь:\(\triangle ABC \sim \triangle EFD\).
Приклад А говорить про те, що для доведення подібності необхідно лише знати, що два відповідних кути рівні:
Два трикутника схожі, якщо два кути одного дорівнюють двом кутам іншого\((AA = AA)\).
На малюнку\(\PageIndex{2}\), \(\triangle ABC \sim \triangle DEF\) because \(\angle A = \angle D\) and \(\angle B = \angle E\).

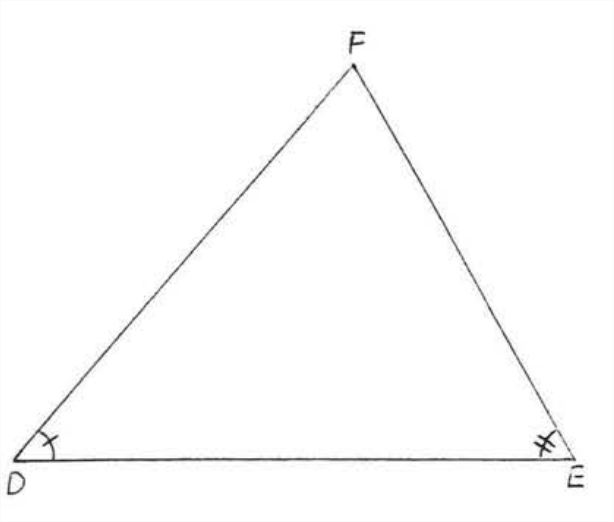
- Доказ
-
\(\triangle C = 180^{\circ} - (\angle A + \angle B) = 180^{\circ} - (\angle D + \angle E) = \angle F\).
Визначте, які трикутники схожі і напишіть заяву подібності:
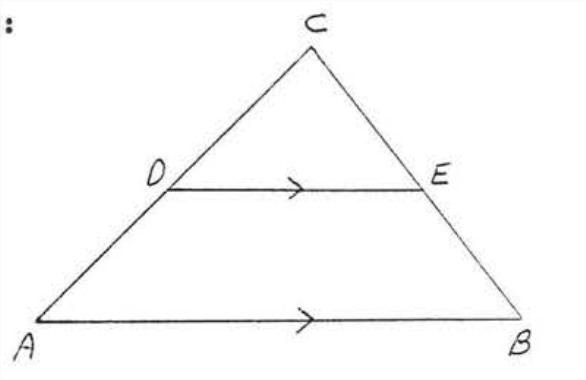
Рішення
\(\angle A = \angle CDE\)тому що вони є відповідними кутами паралельних ліній. \(\angle C = \angle C\)через ідентичність. Тому\(\triangle ABC \sim \triangle DEC\) по\(AA = AA\).
Відповідь:\(\triangle ABC \sim \triangle DEC\).
Визначте, які трикутники схожі і напишіть заяву подібності:

Рішення
\(\angle A=\angle A\)ідентичність. \(\angle ACB = \angle ADC=90^{\circ}\). Тому

Крім того\(\angle B = \angle B\), ідентичність,\(\angle BDC = \angle BCA = 90^{\circ}\). Тому

Відповідь:\(\triangle ABC \sim \triangle ACD \sim \triangle CBD\).
Подібні TriAngies важливі через наступну теорему:
Відповідні сторони подібних трикутників пропорційні. Це означає, що якщо\(\triangle ABC \sim \triangle DEF\) тоді
\(\dfrac{AB}{DE} = \dfrac{BC}{EF} = \dfrac{AC}{DF}\).
Тобто перші дві літери\(\triangle ABC\) є першими двома літерами\(\triangle DEF\) як останні дві літери до\(\triangle ABC\) останніх двох літер\(\triangle DEF\) як перша і остання літери до першої та останньої літер\(\triangle DEF\).\(\triangle ABC\)
Перш ніж намагатися довести теорему\(\PageIndex{2}\), наведемо кілька прикладів того, як вона використовується:
Знайти\(x\):

Рішення
\(\angle A = \angle D\)і\(\angle B = \angle E\) так\(\triangle ABC \sim \triangle DEF\). За теоремою\(\PageIndex{2}\),
\(\dfrac{AB}{DE} = \dfrac{BC}{EF} = \dfrac{AC}{DF}\).
Ми будемо ігнорувати\(\dfrac{AB}{DE}\) тут, оскільки ми не знаємо і не повинні знайти жодного\(AB\) або\(DE\).
\[\begin{array} {rcl} {\dfrac{BC}{EF}} & = & {\dfrac{AC}{DF}} \\ {\dfrac{8}{x}} & = & {\dfrac{2}{3}} \\ {24} & = & {2x} \\ {12} & = & {x} \end{array}\]
Перевірка:

Відповідь:\(x = 12\).
Знайти\(x\):

Рішення
\(\angle A = \angle A, \angle ADE = \angle ABC\), Отже,\(\triangle ADE \sim \triangle ABC\) по\(AA = AA\).
\(\dfrac{AD}{AB} = \dfrac{DE}{BC} = \dfrac{AE}{AC}\).
Ми ігноруємо\(\dfrac{AD}{AB}\).
\[\begin{array} {rcl} {\dfrac{DE}{BC}} & = & {\dfrac{AE}{AC}} \\ {\dfrac{5}{15}} & = & {\dfrac{10}{10 + x}} \\ {5(10 + x)} & = & {15(10)} \\ {50 + 5x} & = & {150} \\ {5x} & = & {150 - 50} \\ {5x} & = & {100} \\ {x} & = & {20} \end{array}\]
Перевірка:

Відповідь:\(x = 20\).
Знайти\(x\):

Рішення
\(\angle A = \angle CDE\)тому що вони є відповідними кутами паралельних ліній. \(\angle C = \angle C\)через ідентичність. Тому\(\triangle ABC \sim \triangle DEC\) по\(AA = AA\).
\(\dfrac{AB}{DE} = \dfrac{BC}{EC} = \dfrac{AC}{DC}\)
Ми ігноруємо\(\dfrac{BC}{EC}\):
\[\begin{array} {rcl} {\dfrac{AB}{DE}} & = & {\dfrac{AC}{DC}} \\ {\dfrac{x + 5}{4}} & = & {\dfrac{x + 3}{3}} \\ {(x + 5)(3)} & = & {(4)(x + 3)} \\ {3x + 15} & = & {4x + 12} \\ {15 - 12} & = & {4x - 3x} \\ {3} & = & {x} \end{array}\]
Перевірка:

Відповідь:\(x = 3\).
Знайти\(x\):

Рішення
\(\angle A = \angle A\),\(\angle ACB = \angle ADC = 90^{\circ}\),\(\triangle ABC \sim \triangle ACD\).
\[\begin{array} {rcl} {\dfrac{AB}{AC}} & = & {\dfrac{AC}{AD}} \\ {\dfrac{x + 12}{8}} & = & {\dfrac{8}{x}} \\ {(x + 12)(x)} & = & {(8)(8)} \\ {x^2 + 12x} & = & {64} \\ {x^2 + 12x - 64} & = & {0} \\ {(x - 4)(x + 16)} & = & {0} \\ {x = 4\ \ \ \ \ \ \ \ x} & = & {-16} \end{array}\]
Ми відхиляємо відповідь,\(x = -16\) тому що\(AD = x\) не може бути негативним.
Перевірте,\(x = 4\)

Відповідь:\(x = 4\).
Дерево кидає тінь довжиною 12 футів в той же час 6 футів людина кидає тінь довжиною 4 фути. Яка висота дерева?

Рішення
На\(AB\) схемі і\(DE\) знаходяться паралельні промені сонця. Тому\(\angle A = \angle D\) тому що вони є відповідними кутами паралельних ліній по відношенню до поперечних\(AF\). Так як також\(\angle C = \angle F = 90^{\circ}\), у нас є\(\triangle ABC \sim \triangle DEF\) по\(AA = AA\).
\[\begin{array} {rcl} {\dfrac{AC}{DF}} & = & {\dfrac{BC}{EF}} \\ {\dfrac{4}{12}} & = & {\dfrac{6}{x}} \\ {4x} & = & {72} \\ {x} & = & {18} \end{array}\]
Відповідь:\(x = 18\) ноги.
Доказ теореми\(\PageIndex{2}\) ("The corresponding sides of similar triangles are proportional"):
Проілюструємо доказ за допомогою трикутників Прикладу\(\PageIndex{4}\) (Figure \(\PageIndex{3}\)). The proof for other similar triangles follows the same pattern. Here we will prove that \(x = 12\) so that \(\dfrac{2}{3} = \dfrac{8}{x}\).


Спочатку намалюйте лінії, паралельні сторонам\(\triangle ABC\) і\(\triangle DEF\) як показано на малюнку,\(\PageIndex{4}\). The corresponding кути цих паралельних ліній рівні і кожен з паралелограмів зі стороною, рівною 1, має свою протилежну сторону, рівну 1, тому всі маленькі трикутники зі стороною, рівною 1, є конгруентний по\(AAS = AAS\). Відповідні сторони цих трикутників утворюють сторону\(\triangle ABC\) (див\(BC = 8\). Рис.\(\PageIndex{5}\)). Therefore each of these sides must equal 4 and \(x = EF = 4 + 4 + 4 = 12\) (Figure \(\PageIndex{6}\)).


(Примітка для інструктора: Це доказ може бути здійснено, коли довжини сторін трикутників є раціональними числами. Однак, оскільки ірраціональні числа можуть бути наближені настільки точно, наскільки це необхідно раціональними, доказ поширюється і на цей випадок.)
Фалес (c. 600 до н.е.) використовував пропорційність сторін подібних трикутників для вимірювання висот пірамід в Єгипті. Його метод був дуже схожий на той, який ми використовували в Example.\(\PageIndex{8}\) to measure the height of trees.
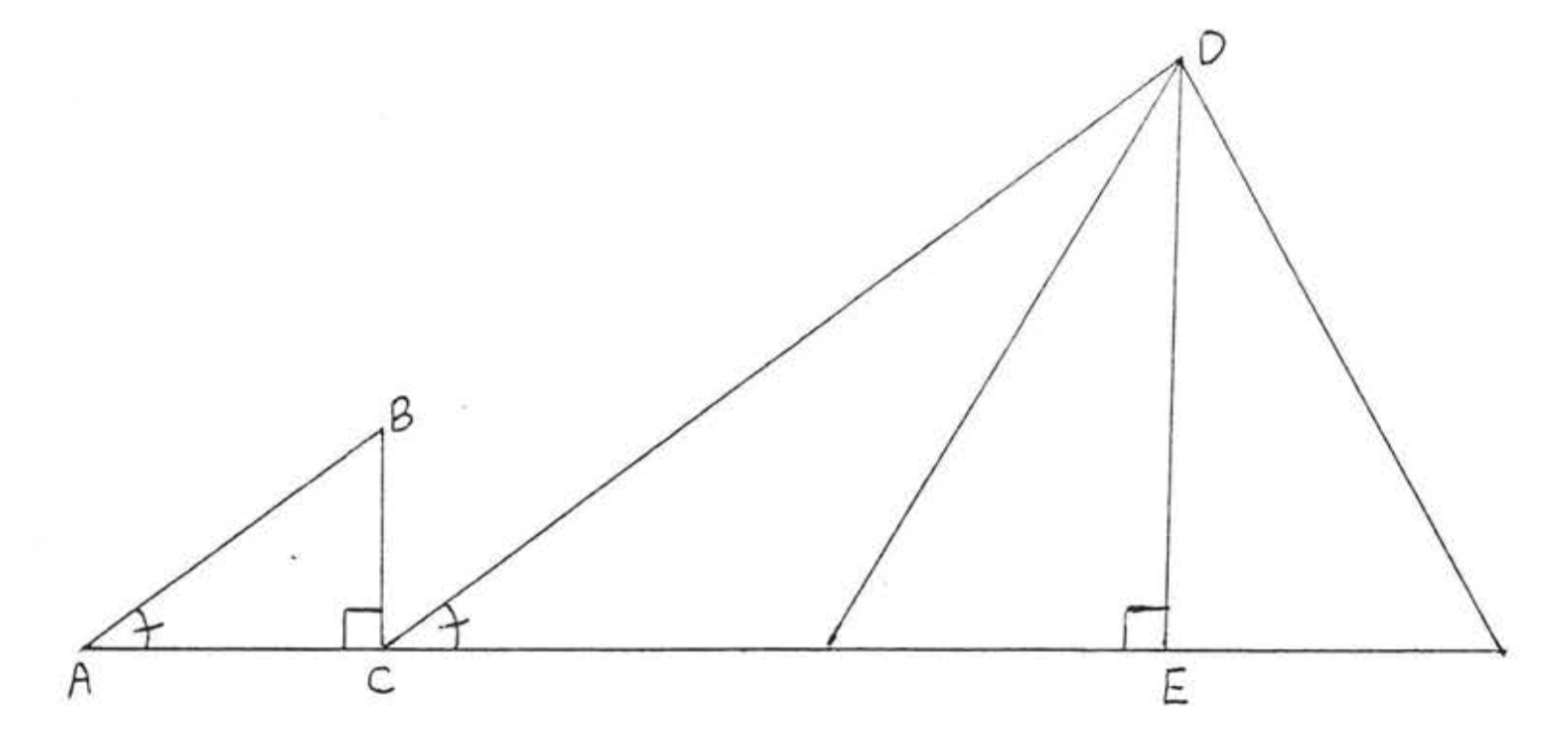
На малюнку\(\PageIndex{7}\), \(DE\) represent the height of the pyramid and \(CE\) is the length of its shadow. \(BC\) represents a vertical stick and \(AC\) is the length of its shadow. We have \(\triangle ABC \sim \triangle CDE\). Thales was able to measure directly the lengths \(AC, BC\), and \(CE\). Substituting these values in the proportion \(\dfrac{BC}{DE} = \dfrac{AC}{CE}\), he was able to find the height \(DE\).
Проблеми
1 - 6. Визначте, які трикутники схожі і напишіть заяву подібності:
1.

2.

3.
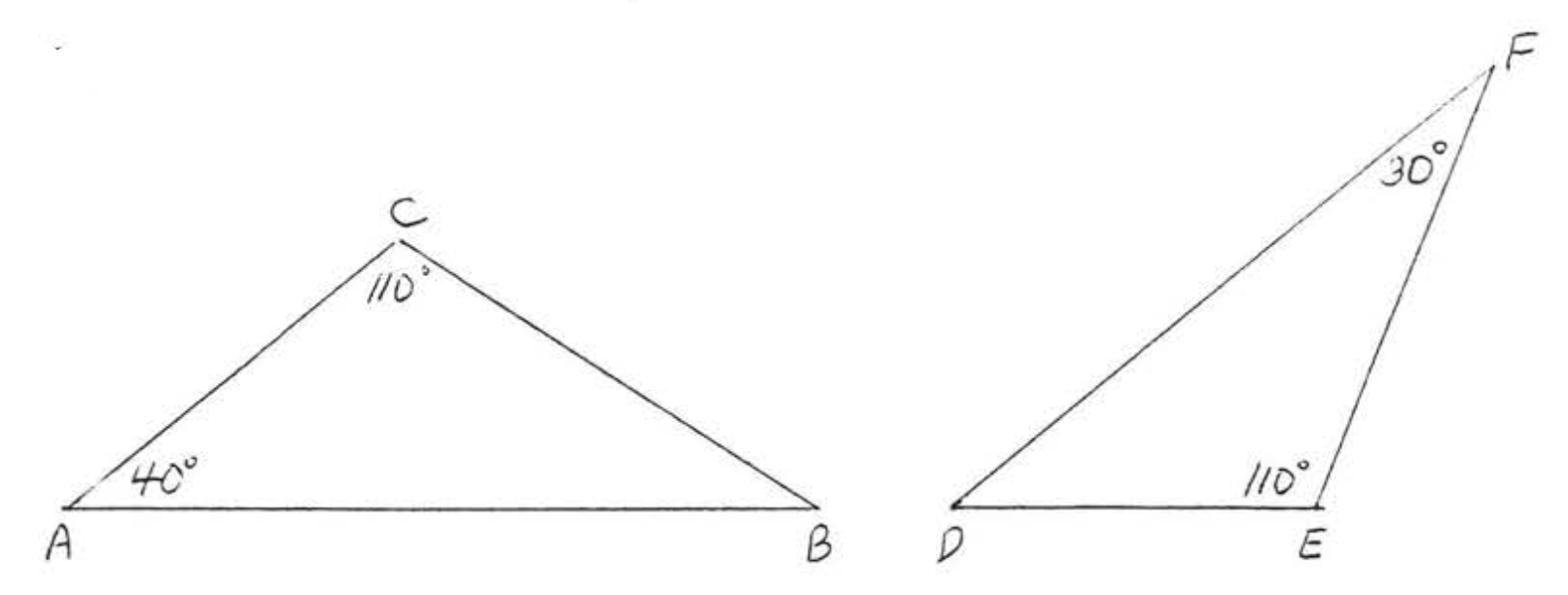
4. 
5.

6.

7 - 22. Для кожного з наступних
(1) написати заяву подібності
(2) напишіть пропорцію між відповідними сторонами
(3) вирішити для\(x\) або\(x\) і\(y\).
7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.
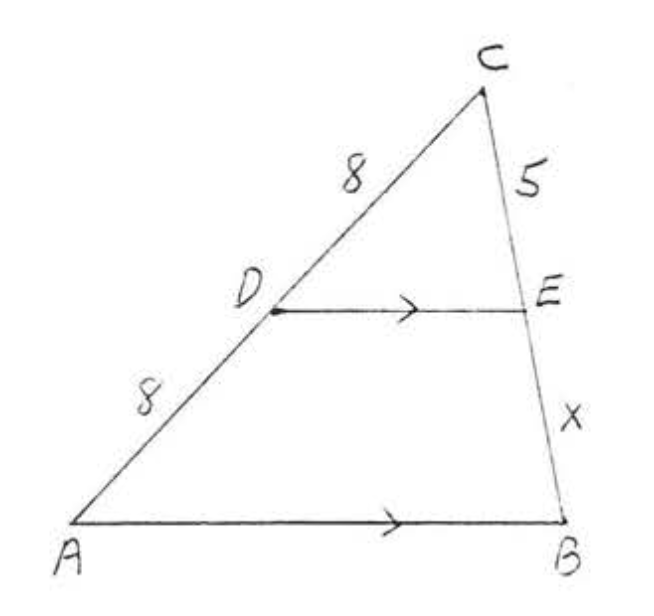
19.

20.

21.

22.

23. Флагшток кидає тінь довжиною 80 футів в той же час 5-футовий хлопчик кидає тінь довжиною 4 фути. Наскільки високий флагшток?
24. Знайдіть\(AB\) ширину річки:

