20.6: Площа твердих паралелограмів

Last updated
Save as PDF

Page ID: 59118

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Теорема$\PageIndex{1}$

$\square ABCD$Дозволяти паралелограм в евклідовій площині,$a=AB$ і$h$ бути відстань між лініями$(AB)$ і$(CD)$. Тоді

$\text{area }(\blacksquare ABCD)=a\cdot h.$

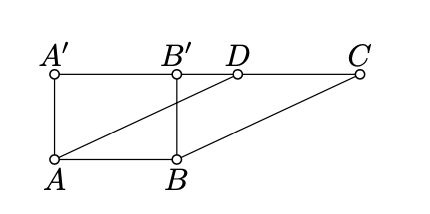
$2021-03-03 9.01.52.PNG$

Доказ

Нехай$A'$ і$B'$ позначають точки стопи$A$ і$B$ на лінії$(CD)$.

Зверніть увагу, що$ABB'A'$ це прямокутник зі сторонами$a$ і$h$. За теоремою 20.5.1

\[\text{area }(\blacksquare ABB'A')=h\cdot a.\]

Без втрати спільності можна вважати, що$\blacksquare ABCA'$ містить$\blacksquare ABCD$ і$\blacksquare ABB'A'$. При цьому$\blacksquare ABCA'$ допускається два підрозділи:

$\blacksquare ABCA'=\blacksquare ABCD\cup\blacktriangle AA'D=\blacksquare ABB'A'\cup\blacksquare BB'C.$

За пропозицією 20.4.2

\[\begin{aligned} \text{area }( \blacksquare ABCD)&+\text{area }(\blacktriangle AA'D)= \\ &= \text{area }(\blacksquare ABB'A')+ \text{area } (\blacktriangle BB'C). \end{aligned}\]

Зверніть увагу, що

Дійсно, оскільки$ABCD$ чотирикутники$ABB'A'$ і паралелограми, по Лемма 7.5.1, ми маємо що$AA'=BB'$$AD=BC$, і$DC=AB=A'B'$. Звідси випливає, що$A'D=B'C$. Застосовуючи умову конгруентності ССС, отримуємо 20.6.3.

Зокрема,

\[\text{area }(\blacktriangle BB'C)=\text{area } (\blacktriangle AA'D). \]

Віднімаючи 20.6.4 з 20.4.2, отримуємо, що

\[\text{area } (\blacksquare ABCD)=\text{area }(\blacksquare ABB'D).\]

Залишилося застосувати 20.6.1.

Вправа$\PageIndex{1}$

Припустимо$\square ABCD$$\square AB'C'D'$ і два паралелограма такі, що$B'\in[BC]$ і$D\in [C'D']$. Покажіть, що

$\text{area }(\blacksquare ABCD)=\text{area }(\blacksquare AB'C'D').$

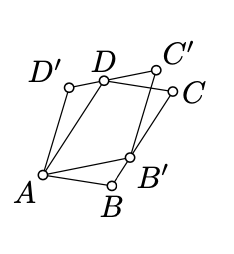
$2021-03-03 пнг$

Підказка

Припустимо, що$E$ позначає точку перетину ліній$(BC)$ і$(C'D')$.

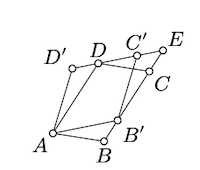
$2021-03-03 пнг$

Використовуйте Proposition,$\PageIndex{1}$ щоб довести наступні дві ідентичності:

$\begin{array} {l} {\text{area } (\blacksquare AB'ED) = \text{area } (\blacksquare ABCD),} \\ {\text{area } (\blacksquare AB'ED) = \text{area } (\blacksquare AB'C'D')} \end{array}$