20.1: Суцільні трикутники

Last updated
Save as PDF

Page ID: 59115

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

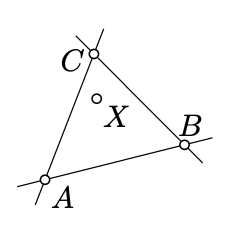
$2021-03-02 пл.$

Ми говоримо, що точка$X$ лежить всередині невиродженого трикутника,$ABC$ якщо дотримуються наступні три умови:

$A$і$X$ лягти на одну сторону від волосіні$(BC)$;
$B$і$X$ лягти на одну сторону від волосіні$(CA)$;
$C$і$X$ лягти на ту ж сторону від лінії$(AB)$.

Безліч всіх точок всередині$\triangle ABC$ і з його сторін$[AB]$$[BC]$,$[CA]$ буде називатися суцільним трикутником$ABC$ і позначено$\blacktriangle ABC$.

Вправа$\PageIndex{1}$

Показати, що будь-який суцільний трикутник опуклий; тобто для будь-якої пари точок$X,Y\in\blacktriangle ABC$, то відрізок лінії$[XY]$ лежить в$\blacktriangle ABC$.

Підказка

Припустимо, навпаки; тобто є$W \in [XY]$ такий момент, що$W \not\in \blacktriangle ABC$.

Без втрати спільності можна вважати, що W і A лежать на протилежних сторонам лінії$(BC)$.

Вона має на увазі, що обидва сегменти$[W X]$ і$[W Y]$ перетинаються$(BC)$. За аксіомою II,$W \in (BC)$ — протиріччя.

Позначення$\triangle ABC$ і$\blacktriangle ABC$ виглядають схожі, вони теж мають близькі, але різні значення, які краще не плутати. Нагадаємо, що$\triangle ABC$ це впорядкована трійка різних точок (див. сторінку), в той час як$\blacktriangle ABC$ являє собою нескінченний набір точок.

Зокрема,$\blacktriangle ABC=\blacktriangle BAC$ для будь-якого трикутника$ABC$. Дійсно, будь-яка точка, яка належить множині,$\blacktriangle ABC$ також належить набору$\blacktriangle BAC$ і навпаки. З іншого боку,$\triangle ABC \ne \triangle BAC$ просто тому, що впорядкована трійка очок$(A,B,C)$ відрізняється від впорядкованої трійки$(B,A,C)$.

Відзначимо$\triangle ABC\ncong\triangle BAC$, що$\blacktriangle ABC\cong\blacktriangle BAC$ навіть якщо, де конгруентність множин$\blacktriangle ABC$ і$\blacktriangle BAC$ розуміється наступним чином:

Визначення$\PageIndex{1}$

Два$\mathcal{S}$ множини і$\mathcal{T}$ в площині називаються конгруентними (коротко$\mathcal{S}\cong \mathcal{T}$), якщо$\mathcal{T}=f(\mathcal{S})$ для$f$ деякого руху площини.

Якщо$\triangle ABC$ не вироджується і

$\blacktriangle ABC\cong \blacktriangle A'B'C',$

то після позначення вершин$\triangle ABC$ ми матимемо

$\triangle ABC\cong \triangle A'B'C'.$

Дійсно, достатньо показати, що якщо$f$ це рух, який$\blacktriangle ABC$ відображає$\blacktriangle A'B'C'$, то$f$ відображає кожну вершину$\triangle ABC$ до вершини$\triangle A'B'C'$. Останнє випливає з характеристики вершин твердих трикутників, наведеної в наступній вправі:

Вправа$\PageIndex{1}$

$\triangle ABC$Дозволяти бути невиродженим і$X\in \blacktriangle ABC$. Показати, що$X$ є вершиною$\triangle ABC$ if і тільки якщо є лінія$\ell$, яка перетинається$\blacktriangle ABC$ в одній точці$X$.

Підказка

Щоб довести частину «тільки якщо», розглянемо лінію, що проходить через вершину, паралельну протилежній стороні.

Щоб довести частину «якщо», скористайтеся теоремою Паша (теорема 3.4.1).

Вправа\(\PageIndex{1}\)

Визначення\(\PageIndex{1}\)

Вправа\(\PageIndex{1}\)