20.7: Площа твердих трикутників

Last updated
Save as PDF

Page ID: 59123

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Теорема$\PageIndex{1}$

Нехай$a=BC$ і$h_A$ бути висотою від$A$ в$\triangle ABC$. Тоді

$\text{area }(\blacktriangle ABC)=\tfrac12\cdot a\cdot h_A.$

Доказ

Намалюйте лінію$m$ через$A$, яка є$(BC)$ паралельною і лінію$n$ через$C$ паралельно$(AB)$. Зверніть увагу, що лінії$m$ і$n$ не паралельні; позначають по$D$ їх точці перетину. За конструкцією,$\square ABCD$ являє собою паралелограм.

Зверніть увагу, що$\blacksquare ABCD$ допускає підрозділ на$\blacktriangle ABC$ і$\blacktriangle CDA$. Тому,\[\text{area }(\blacksquare ABCD) = \text{area }(\blacktriangle ABC) + \text{area }(\blacktriangle CDA)\]

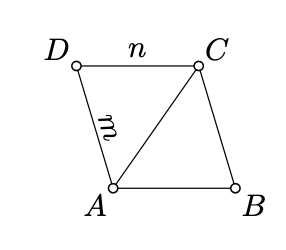
$2021-03-03 пнг$

Оскільки$\square ABCD$ це паралелограм, Lemma 7.5.1 означає, що

$AB=CD \quad \text{and} \quad BC=DA.$

Тому за умовою конгруентності SSS ми маємо$\triangle ABC\cong\triangle CDA$. Зокрема

$\text{area }(\blacktriangle ABC) = \text{area }(\blacktriangle CDA).$

Зверху і Пропозиція 20.6.1, ми отримуємо, що

$\begin{aligned} \text{area }(\blacktriangle ABC) &=\tfrac12\cdot\text{area }(\blacksquare ABCD)= \\ &=\tfrac12\cdot h_A\cdot a\end{aligned}$

Вправа$\PageIndex{1}$

Дозволяти$h_A$$h_B$, і$h_C$ позначають висоти$\triangle ABC$ від вершин$A$,$B$ і$C$ відповідно. Зверніть увагу, що з теореми$\PageIndex{1}$ випливає, що

$h_A\cdot BC=h_B\cdot CA=h_C\cdot AB.$

Дайте доказ цього твердження без використання області.

Підказка

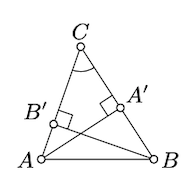
$2021-03-03 пнг$

Без втрати спільності можна вважати, що кути$ABC$ і$BCA$ є гострими.

Нехай$A'$ і$B'$ позначають точки стопи$A$ і$B$ далі$(BC)$ і$(AC)$ відповідно. Зверніть увагу, що$h_A = AA'$ і$h_B = BB'$.

Зауважте, що$\triangle AA'C \sim \triangle BB'C$; дійсно кут під$C$ спільним, а кути в$A'$ і$B'$ є правильними. Зокрема$\dfrac{AA'}{BB'} = \dfrac{AC}{BC}$ або, що еквівалентно,$h_A \cdot BC = h_B \cdot AC$.

Вправа$\PageIndex{2}$

Припустимо$M$ лежить всередині паралелограма$ABCD$; тобто$M$ належить суцільному паралелограму$\blacksquare ABCD$, але не лежить на його боках. Покажіть, що

$\text{area }(\blacktriangle ABM)+\text{area }(\blacktriangle CDM) =\tfrac12\cdot \text{area }(\blacksquare ABCD).$

Підказка

Намалюйте$\ell$ лінію$M$ паралельно$[AB]$ і$[CD]$; вона$\blacksquare ABCD$ поділяє на два суцільних паралелограма, які будуть$\blacksquare ABEF$ позначені і$\blacksquare CDFE$. Зокрема,

$\text{area } (\blacksquare ABCD) = \text{area } (\blacksquare ABEF) + \text{area } (\blacksquare CDFE)$.

За пропозицією 20.6.1 і теоремою$\PageIndex{1}$ ми отримуємо, що

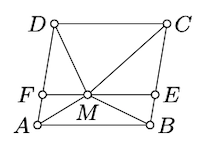
$2021-03-03 9.38.29.png$

$\begin{array} {l} {\text{area } (\blacktriangle ABM) = \dfrac{1}{2} \cdot \text{area } (\blacksquare ABEF),} \\ {\text{area } (\blacktriangle CDM) = \dfrac{1}{2} \cdot \text{area } (\blacksquare CDFE)} \end{array}$

а значить і результат.

Вправа$\PageIndex{3}$

Припустимо, що діагоналі невиродженого чотирикутника$ABCD$ перетинаються в точці$M$. Покажіть, що

$\text{area }(\blacktriangle ABM)\cdot\text{area }(\blacktriangle CDM) = \text{area }(\blacktriangle BCM)\cdot\text{area }(\blacktriangle DAM).$

Підказка

Нехай$h_A$ і$h_C$ позначають відстані від$A$ і$C$ до лінії$(BD)$ відповідно. Згідно з теоремою$\PageIndex{1}$,

$\text{area }(\blacktriangle ABM) = \dfrac{1}{2} \cdot h_A \cdot BM$;$\text{area }(\blacktriangle BCM) = \dfrac{1}{2} \cdot h_C \cdot BM$
$\text{area }(\blacktriangle CDM) = \dfrac{1}{2} \cdot h_C \cdot DM$;$\text{area }(\blacktriangle ABM) = \dfrac{1}{2} \cdot h_A \cdot DM$.

Тому

$\begin{array} {rcl} {\text{area } (\blacktriangle ABM) \cdot \text{area } (\blacktriangle CDM)} & = & {\dfrac{1}{4} \cdot h_A \cdot h_C \cdot DM \cdot BM =} \\ {} & = & {\text{area } (\blacktriangle BCM) \cdot \text{area } (\blacktriangle DAM)} \end{array}$

Вправа$\PageIndex{4}$

$r$Дозволяти бути радіус$\triangle ABC$ інерції і$p$ бути його напівпериметр; тобто,$p=\tfrac12\cdot(AB+BC+CA)$. Покажіть, що

$\text{area }(\blacktriangle ABC)=p\cdot r.$

Підказка

$I$Дозволяти бути в центрі$\triangle ABC$. Відзначимо, що$\blacktriangle ABC$ можна поділити на$\blacktriangle IAB, \blacktriangle IBC$ і$\blacktriangle ICA$.

Залишилося застосувати теорему$\PageIndex{1}$ до кожного з цих трикутників і підвести підсумки.

Вправа$\PageIndex{5}$

Показати, що будь-яка багатокутна множина допускає поділ на скінченну колекцію твердих трикутників і вироджену множину. Зробіть висновок, що для будь-якої багатокутної множини його площа однозначно визначена.

Підказка: Закріпіть багатокутний набір$\mathcal{P}$. Без втрати спільності можна припустити, що$\mathcal{P}$ це об'єднання скінченної колекції твердих трикутників. Розрізаємо$\mathcal{P}$ уздовж розширень сторін все трикутники, його поділяють$\mathcal{P}$ на опуклі багатокутники. Розрізання кожного багатокутника по діагоналям з однієї вершини виробляють поділ на суцільні трикутники.

Теорема\(\PageIndex{1}\)

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)

Вправа\(\PageIndex{3}\)

Вправа\(\PageIndex{4}\)

Вправа\(\PageIndex{5}\)