20.5: Площа суцільних прямокутників

Last updated
Save as PDF

Page ID: 59120

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Теорема$\PageIndex{1}$

Суцільний прямокутник зі сторонами$a$ і$b$ має площу$a\cdot b$.

Доказ

Припустимо, що$\mathcal{R}_{a,b}$ позначає суцільний прямокутник зі сторонами$a$ і$b$. Набір

$s(a,b)=\text{area } \mathcal{R}_{a,b}.$

За визначенням площі,$s(1,1)=\text{area }(\mathcal{K})=1$. Тобто перша ідентичність в алгебраїчній лемі тримає.

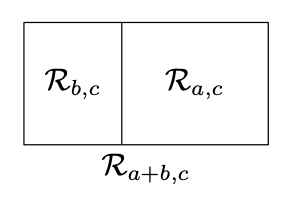
$2021-03-03 пнг$

Зверніть увагу, що прямокутник$\mathcal{R}_{a+b,c}$ можна розділити на два прямокутника, що збігаються з$\mathcal{R}_{a,c}$ і$\mathcal{R}_{b,c}$. Тому, за пропозицією 20.4.2,

$\text{area }\mathcal{R}_{a+b,c}=\text{area } \mathcal{R}_{a,c}+\text{area } \mathcal{R}_{b,c}$

Тобто друга ідентичність в алгебраїчній лемі тримає. Доказом третьої особи є аналоги.

Залишилося застосувати алгебраїчну лему.

Лемма$\PageIndex{1}$ Algebraic lemma

Припустімо, що функція$s$ повертає невід'ємне дійсне число$s(a,b)$ для будь-якої пари позитивних дійсних чисел$(a,b)$ і задовольняє такі ідентичності:

$\begin{aligned} s(1,1)&=1; \\ s(a,b+c)&=s(a,b)+s(a,c) \\ s(a+b,c)&=s(a,c)+s(b,c)\end{aligned}$

для будь-якого$a,b,c>0$. Тоді

$s(a,b)=a\cdot b$

для будь-якого$a,b>0$.

Доказ схожий на доказ Лемми 14.4.1.

Доказ

Зверніть увагу, що якщо$a>a'$ і$b>b'$ тоді

\[s(a,b)\ge s(a',b').\]

Дійсно, оскільки$s$ повертає невід'ємні числа, ми отримуємо, що

$\begin{aligned} s(a,b)&=s(a',b)+s(a-a',b)\ge \\ &\ge s(a',b)= \\ &\ge s(a',b')+s(a',b-b')\ge \\ &\ge s(a',b').\end{aligned}$

Застосовуючи другу та третю особистість кілька разів, ми отримуємо це

$\begin{aligned} s(a,m\cdot b)=s(m\cdot a,b)=m\cdot s(a,b)\end{aligned}$

для будь-якого натурального цілого числа$m$. Тому

$\begin{aligned} s(\tfrac kl,\tfrac mn)&=k \cdot s(\tfrac 1l,\tfrac mn)= \\ &=k\cdot m \cdot s(\tfrac 1l,\tfrac 1n)= \\ &=k\cdot m\cdot \tfrac 1l\cdot s(1, \tfrac 1n)= \\ &=k\cdot m\cdot \tfrac 1l\cdot \tfrac 1n\cdot s(1,1)= \\ &=\tfrac kl\cdot\tfrac mn\end{aligned}$

для будь-яких натуральних чисел$k$,$l$,$m$, і$n$. Тобто необхідна ідентичність тримає для будь-якої пари раціональних чисел$a=\tfrac kl$ і$b=\tfrac mn$.

Аргументуючи протиріччям, припустимо$s(a,b)\ne a\cdot b$ для деякої пари позитивних дійсних чисел$(a,b)$. Ми розглянемо два випадки:$s(a,b)> a\cdot b$ і$s(a,b)< a\cdot b$.

Якщо$s(a,b)> a\cdot b$, ми можемо вибрати натуральне число$n$ таке, що

\[s(a,b)> (a+\tfrac1n)\cdot (b+\tfrac1n).\]

Встановити$k=\lfloor a\cdot n \rfloor+1$ і$m=\lfloor b\cdot n \rfloor+1$; еквівалентно,$k$ і$m$ є додатними цілими числами такими, що

$a< \tfrac kn\le a+\tfrac1n \quad\text{and}\quad b<\tfrac mn\le b+\tfrac1n.$

До 20.5.1 ми отримуємо, що

$\begin{aligned} s(a,b)&\le s(\tfrac kn,\tfrac mn)= \\ &=\tfrac kn\cdot\tfrac mn\le \\ &\le (a+\tfrac1n)\cdot(b+\tfrac1n),\end{aligned}$

що суперечить 20.5.2.

Справа$s(a,b)< a\cdot b$ аналогічна. Виправте додатне ціле число,$n$ таке$a>\tfrac1n$, що$b>\tfrac1n$, і

\[s(a,b)< (a-\tfrac1n)\cdot (b-\tfrac1n).\]

Встановити$k=\lceil a\cdot n \rceil-1$ і$m=\lceil b\cdot n \rceil-1$; тобто,

$a> \tfrac kn\ge a-\tfrac1n \quad\text{and}\quad b>\tfrac mn\ge b-\tfrac1n.$

Застосовуючи 20.5.1 знову, ми отримуємо, що

$\begin{aligned} s(a,b)&\ge s(\tfrac kn,\tfrac mn)= \\ &=\tfrac kn\cdot\tfrac mn\ge \\ &\ge (a-\tfrac1n)\cdot(b-\tfrac1n),\end{aligned}$

що суперечить 20.5.3.