20.8: Метод площі

Last updated
Save as PDF

Page ID: 59109

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У цьому розділі ми наведемо приклади тонких доказів з використанням властивостей площі. Зверніть увагу, що ці докази не є справді елементарними, оскільки ціна, яку платить за введення функції площі, висока.

Почнемо з доказу теореми Піфагора. У Елементах Евкліда теорема Піфагора була сформульована як рівність 20.8.1 нижче, і доказ використовував подібну методику.

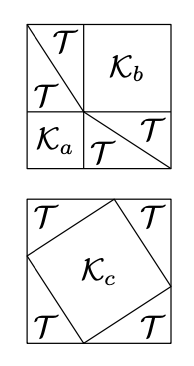
$2021-03-03 пнг$

Доказ. Потрібно показати, що якщо$a$ і$b$ є катетами і$c$ є гіпотенузою прямокутного трикутника, то

$a^2+b^2=c^2.$

Припустимо, що$\mathcal{T}$ позначає правильний суцільний трикутник з ніжками$a$$b$ і$\mathcal{K}_{x}$ суцільний квадрат зі стороною$x$.

Побудуємо два підрозділи$\mathcal{K}_{a+b}$:

$\mathcal{K}_{a+b}$Розділіть на два тверді квадрати, конгруентні до$\mathcal{K}_a$$\mathcal{K}_b$ і 4 твердих трикутників, конгруентних до$\mathcal{T}$, див. Перша діаграма.
$\mathcal{K}_{a+b}$Розділіть на один суцільний квадрат, конгруентний до$\mathcal{K}_c$ і 4 суцільних прямокутних трикутників, конгруентних до$\mathcal{T}$, див. Другу діаграму.

Застосовуючи пропозицію 20.4.2 кілька разів, ми отримуємо це

$\begin{aligned} \text{area }\mathcal{K}_{a+b} &= \text{area }\mathcal{K}_{a}+\text{area } \mathcal{K}_{b} +4\cdot\text{area }\mathcal{T}= \\ &=\text{area }\mathcal{K}_{c}+4\cdot\text{area }\mathcal{T}.\end{aligned}$

Тому,

\[\text{area }\mathcal{K}_{a}+\text{area }\mathcal{K}_{b}=\text{area }\mathcal{K}_{c}.\]

За теоремою 20.5.1

$\text{area }\mathcal{K}_x=x^2,$

для будь-якого$x>0$. Звідси випливає твердження.

Вправа$\PageIndex{1}$

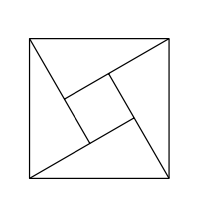
Побудуйте ще один доказ теореми Піфагора на основі діаграми.

(У позначеннях вище він показує підрозділ$\mathcal{K}_c$ на$\mathcal{K}_{a-b}$ і чотири копії$\mathcal{T}$ if$a>b$.)

$2021-03-03 10.03.42 пнг$

Підказка

Припускаючи$a > b$, що ми$\mathcal{Q}_c$ поділяємо на$\mathcal{Q}_{a - b}$ і чотири трикутники, конгруентні до$\mathcal{T}$. Тому

\[\text{area } \mathcal{Q}_c = \text{area } \mathcal{Q}_{a - b} + 4 \cdot \text{area } \mathcal{T}.\]

Відповідно до теореми 20.7.1,$\text{area } \mathcal{T} = \tfrac{1}{2} \cdot a \cdot b$. Тому посвідчення 20.8.2 можна записати як

$c^2 = (a - b)^2 + 2 \cdot a \cdot b.$

Спрощуючи, отримаємо теорему Піфагора.

Справа все$a = b$ ж простіше. Справа$b > a$ можна зробити так само.

Вправа$\PageIndex{2}$

Показати, що сума відстаней від точки до сторін рівностороннього трикутника однакова для всіх точок всередині трикутника.

Підказка

Якщо$X$ є точкою всередині$\triangle ABC$, то$\blacktriangle ABC$ підрозділяється на$\blacktriangle ABX$,$\blacktriangle BCX$, і$\blacktriangle CAX$. Тому

$\text{area } (\blacktriangle ABX) + \text{area } (\blacktriangle BCX) + \text{area } (\blacktriangle CAX) = \text{area } (\blacktriangle ABC).$

Набір$a = AB = BC = CA$. Нехай$h_1, h_2$, і$h_3$ позначають відстані від$X$ до сторін$[AB]$$[BC]$, і$[CA]$. Тоді за теоремою 20.7.1,

$\text{area } (\blacktriangle ABX) = \dfrac{1}{2} \cdot h_1 \cdot a$,$\text{area } (\blacktriangle BCX) = \dfrac{1}{2} \cdot h_2 \cdot a$,$\text{area } (\blacktriangle CAX) = \dfrac{1}{2} \cdot h_3 \cdot a$.

Тому,

$h_1 + h_2 + h_3 = \dfrac{2}{a} \cdot \text{area } (\blacktriangle ABC).$

Претензія$\PageIndex{1}$

Припустимо, що два трикутника$ABC$ і$A'B'C'$ в евклідовій площині мають рівні висоти, скинуті з$A$ і$A'$ відповідно. Тоді

\[\dfrac{\text{area }(\blacktriangle A'B'C')}{\text{area }(\blacktriangle ABC)} = \dfrac{B'C'}{BC}.\]

Зокрема, одна і та ж ідентичність тримає, якщо$A=A'$ і$[BC]$ підстави і$[B'C']$ лежать на одній лінії.

Доказ

$h$Дозволяти висоті. За теоремою 20.7.1

$\dfrac{\text{area }(\blacktriangle A'B'C')}{\text{area }(\blacktriangle ABC)} = \dfrac{\frac12 \cdot h\cdot B'C'}{\frac12 \cdot h\cdot BC} = \dfrac{B'C'}{BC}.$

Тепер давайте покажемо, як використовувати цю претензію, щоб довести Lemma 8.4.1. Для початку нагадаємо його твердження:

Лемма 8.4.1

If$\triangle ABC$ є невиродженим і його кут$A$ бісектриса на перетині$[BC]$ і точці$D$. Тоді

$\dfrac{AB}{AC} =\dfrac{DB}{DC}.$

Доказ

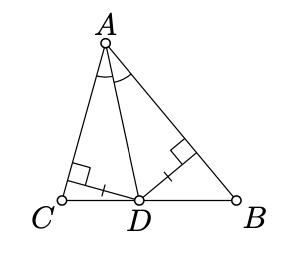
$2021-03-03 пнг$

Застосовуючи претензію$\PageIndex{1}$, ми отримуємо, що

$\dfrac{\text{area } (\blacktriangle ABD)}{\text{area } (\blacktriangle ACD)} = \dfrac{BD}{CD}.$

За пропозицією 8.10 трикутники$ABD$ і$ACD$ мають рівні висоти від$D$. Застосовуючи претензію$\PageIndex{1}$ знову, ми отримуємо, що

$\dfrac{\text{area } (\blacktriangle ABD)}{\text{area } (\blacktriangle ACD)} = \dfrac{AB}{AC}.$

а значить і результат.

Припустимо,$ABC$ це невироджений трикутник і$A'$ лежить між$B$ і$C$. У цьому випадку відрізок лінії$[AA']$ називається cevian (він названий на честь Джованні Чеви і вимовляється як chevian.)$\triangle ABC$ at$A$. Друге твердження в наступній вправі називається теоремою Чеви.

Вправа$\PageIndex{3}$

$ABC$Дозволяти бути невиродженим трикутником. Припустимо, його севіани$[AA']$,$[BB']$ і$[CC']$ перетинаються в одній точці$X$. Покажіть, що

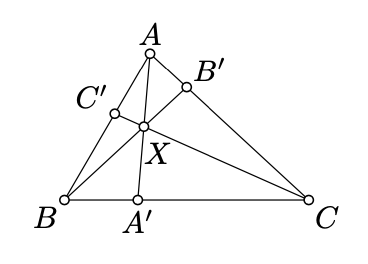
$2021-03-03 пнг$

$\begin{aligned} \frac{\text{area }(\blacktriangle ABX)}{\text{area }(\blacktriangle BCX)}&=\frac{AB'}{B'C}, \\ \frac{\text{area }(\blacktriangle BCX)}{\text{area }(\blacktriangle CAX)}&=\frac{BC'}{C'A}, \\ \frac{\text{area }(\blacktriangle CAX)}{\text{area }(\blacktriangle ABX)}&=\frac{CA'}{A'B} .\end{aligned}$

Зробіть висновок, що

$\dfrac{AB'\cdot CA'\cdot BC'}{B'C\cdot A'B\cdot C'A}=1.$

Підказка

Застосувати претензію$\PageIndex{1}$, щоб показати, що

$\dfrac{\text{area } (\blacktriangle ABB')}{\text{area } (\blacktriangle BCB')} = \dfrac{\text{area } (\blacktriangle AXB')}{\text{area } (\blacktriangle XCB')} = \dfrac{AB'}{B'C}$.

І спостерігайте, що

$\text{area } (\blacktriangle ABB') = \text{area } (\blacktriangle ABX) + \text{area } (\blacktriangle AXB')$,
$\text{area } (\blacktriangle BCB') = \text{area } (\blacktriangle BCX) + \text{area } (\blacktriangle XCB')$.

Вона має на увазі першу ідентичність; решта аналогічна.

Вправа$\PageIndex{4}$

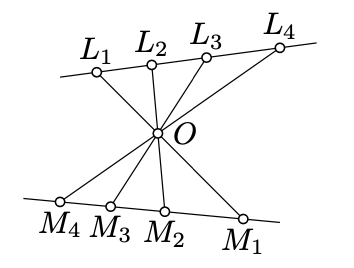
$2021-03-03 пнг$

Припустимо$L_1$, що точки$L_2$$L_3$,,,$L_4$ лежать на лінії$\ell$ і точки$M_1$$M_2$,$M_3$,,$M_4$ лежать на лінії $m$. Припустимо$(L_1M_1)$, що лінії$(L_2M_2)$$(L_3M_3)$,,, і$(L_4M_4)$ пройти через точку$O$, яка не лежить$\ell$ ні на ні$m$.

Застосуйте претензії,$\PageIndex{1}$ щоб показати, що\[\frac{\text{area }\blacktriangle OL_iL_j}{\text{area }\blacktriangle OM_iM_j}=\frac{OL_i\cdot OL_j}{OM_i\cdot OM_j}\] для будь-якого$i\ne j$.
Використовуйте (а), щоб довести,\[\frac{L_1L_2\cdot L_3L_4}{L_2L_3\cdot L_4L_1}=\frac{M_1M_2\cdot M_3M_4}{M_2M_3\cdot M_4M_1};\] що тобто чотирикратні$(L_1, L_2, L_3, L_4)$ і$(M_1, M_2, M_3, M_4)$ мають однакове перехресне відношення.

Підказка

Щоб довести (а), застосуйте Claim$\PageIndex{1}$ двічі до трикутників$OL_iL_j, OL_jM_i$, і$OM_iM_j$.

Щоб довести частину (b), використовуйте Claim,$\PageIndex{1}$ щоб переписати ліву частину, використовуючи області трикутників$OL_1L_2, OL_2L_3, OL_3L_4$, і$OL_4L_1$. Далі використовуйте частину (a), щоб переписати її за допомогою областей$OM_1M_2, OM_2M_3,OM_3M_4$,$OM_4M_1$ і застосуйте$\PageIndex{1}$ Claim знову, щоб отримати праву сторону.

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)

Претензія\(\PageIndex{1}\)

Лемма 8.4.1

Вправа\(\PageIndex{3}\)

Вправа\(\PageIndex{4}\)