13.8: Лаплас зворотний
- Page ID
- 62642
До цих пір ми обчислили зворотне перетворення Лапласа за допомогою пошуку таблиці. Наприклад,\(\mathcal{L}^{-1} (1/(s - a)) = e^{at}\). Щоб зробити це правильно, спочатку слід перевірити, чи перетворення Лапласа має зворотне.
Ми починаємо з поганих новин: На жаль, це не зовсім так. Є багато функцій з однаковим перетворенням Лапласа. Перерахуємо деякі способи, як це може статися.
- Якщо\(f(t) = g(t)\) для\(t \ge 0\), то зрозуміло\(F(s) = G(s)\). Оскільки перетворення Лапласа стосується лише\(t \ge 0\), функції можуть повністю відрізнятися для\(t < 0\).
- Припустимо\(f(t) = e^{at}\), і
\[g(t) = \begin{cases} f(t) & \text{ for } t \ne 1 \\ 0 & \text{ for } t = 1. \end{cases}\]
Тобто\(f\) і\(g\) є однаковими, за винятком того, що ми довільно присвоювали їм різні значення в\(t = 1\). Тоді, оскільки інтеграли не помітять різниці в одній точці,\(F(s) = G(s) = 1/(s - a)\). У цьому сенсі неможливо\(\mathcal{L}^{-1} (F)\) однозначно визначити.
Хороша новина полягає в тому, що зворотне існує до тих пір, поки ми розглядаємо дві функції, які відрізняються лише на незначній множині точок однаково. Зокрема, ми можемо пред'явити наступну претензію.
Припустимо\(g\),\(f\) і є безперервними і\(F(s) = G(s)\) для всіх\(s\) з\(\text{Re} (s) > a\) для деяких\(a\). Тоді\(f(t) = g(t)\) для\(t \ge 0\).
Ця теорема може бути викладена таким чином, що включає в себе кусково-неперервні функції. Таке твердження вимагає більшої обережності, що затьмарює основний момент, що перетворення Лапласа має унікальну зворотну аж до деяких, для нас, тривіальних відмінностей.
Почнемо з кількох прикладів, які ми можемо обчислити безпосередньо.
Нехай
\[f(t) = e^{at}.\]
Отже,
\[F(s) = \dfrac{1}{s - a}.\]
Показати
\[f(t) = \sum \text{Res} (F(s) e^{st})\]
\[f(t) = \dfrac{1}{2\pi i} \int_{c - i\infty}^{c + i \infty} F(s) e^{st}\ ds\]
Сума знаходиться над усіма полюсами\(e^{st}/(s - a)\). Як завжди, ми тільки розглядаємо\(t > 0\).
Тут\(c > \text{Re} (a)\) і інтеграл означає шлях інтеграл по вертикальній лінії\(x = c\).
Рішення
Доведення рівняння 13.8.4 є простим: Зрозуміло, що
\[\dfrac{e^{st}}{s -a}\]
має тільки один полюс, який знаходиться на\(s = a\). З тих пір,
\[\sum \text{Res} (\dfrac{e^{st}}{s - a}, a) = e^{at}\]
ми довели рівняння 13.8.4.
Доведення рівняння 13.8.5 більше бере участь. Спочатку слід перевірити збіжність інтеграла. У цьому випадку, таким чином\(s = c + iy\), інтеграл є
\[\dfrac{1}{2\pi i} \int_{c - i \infty}^{c + i \infty} F(s) e^{st} \ ds = \dfrac{1}{2\pi i} \int_{-\infty}^{\infty} \dfrac{e^{(c + iy)t}}{c + iy - a} i \ dy = \dfrac{e^{ct}}{2 \pi} \int_{-\infty}^{\infty} \dfrac{e^{iyt}}{c + iy - a} \ dy.\]
(умовна) збіжність цього інтеграла випливає з використанням точно такого ж аргументу, що і в прикладі наприкінці теми 9 за формулою інверсії Фур'є для\(f(t) = e^{at}\). Тобто, integrand - це загасаюче коливання, близько 0, тому його інтеграл також є загасаючим коливанням навколо деякого граничного значення.
Тепер використовуємо контур, показаний нижче.
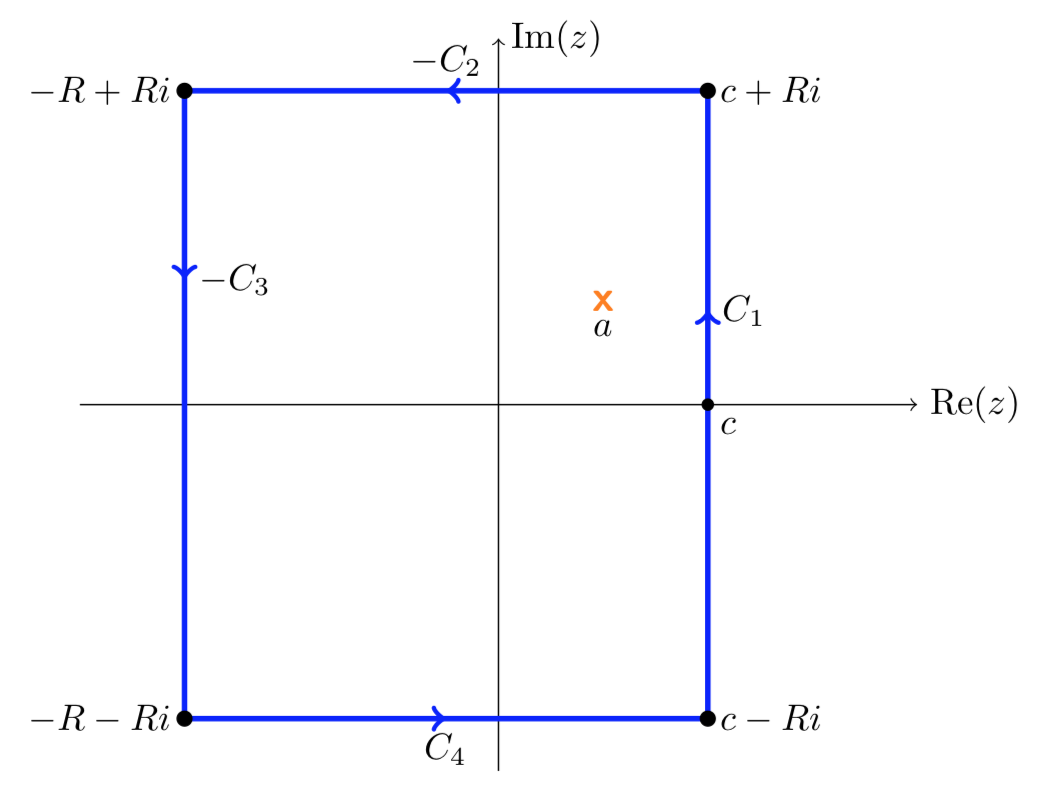
Ми\(R\) відпустимо до нескінченності і використаємо наступні кроки, щоб довести Рівняння 13.8.5.
- Теорема залишку гарантує, що якщо крива досить велика, щоб містити,\(a\) то
\[\dfrac{1}{2\pi i} \int_{C_1 - C_2 - C_3 + C_4} \dfrac{e^{st}}{s - a}\ ds = \sum \text{Res} (\dfrac{e^{st}}{s - a}, a) = e^{at}.\] - Через мить ми покажемо, що інтеграли над\(C_2, C_3, C_4\) усіма йдуть до 0 як\(R \to \infty\).
- Зрозуміло, що\(R\) йде до нескінченності, інтеграл\(C_1\) переходить до інтегралу в рівнянні 13.8.5 Поклавши ці кроки разом, ми маємо
\[e^{at} = \lim_{R \to \infty} \int_{C_1 - C_2 - C_3 + C_4} \dfrac{e^{st}}{s - a} \ ds = \int_{c - i\infty}^{c + i\infty} \dfrac{e^{st}}{s - a} \ ds\]
За винятком доказів у кроці 2, це доводить рівняння 13.8.5.
Щоб перевірити крок 2, ми дивимося на одну сторону за раз.
\(C_2\):\(C_2\) параметризується\(s = \gamma (u) = u + iR\), с\(-R \le u \le c\). Отже,
\[|\int_{C_2} \dfrac{e^{st}}{s - a} \ ds| = \int_{-R}^{c} |\dfrac{e^{(u + iR)t}}{u + iR - a}| \le \int_{-R}^{c} \dfrac{e^{ut}}{R} \ du = \dfrac{e^{ct} - e^{-Rt}}{tR}.\]
Оскільки\(c\) і\(t\) фіксуються, зрозуміло, що це йде до 0, як\(R\) йде до нескінченності.
Низ\(C_4\) обробляється точно так само, як і верх\(C_2\).
\(C_3\):\(C_3\) параметризується\(s = \gamma (u) = -R + iu\), с\(-R \le u \le R\). Отже,
\[|\int_{C_3} \dfrac{e^{st}}{s - a} \ ds| = \int_{-R}^{R} |\dfrac{e^{(-R + iu)t}}{-R + iu - a}| \le \int_{-R}^{R} \dfrac{e^{-Rt}}{R + a} \ du = \dfrac{e^{-Rt}}{R + a} \int_{-R}^{R} \ du = \dfrac{2\text{Re}^{-Rt}}{R+a}.\]
Оскільки\(a\) і\(t > 0\) фіксуються, зрозуміло, що це йде до 0, як\(R\) йде до нескінченності.
Повторіть попередній приклад з\(f(t) = t\) for\(t > 0\),\(F(s) = 1/s^2\).
Це аналогічно попередньому прикладі. Оскільки\(F\) розпади, як\(1/s^2\) ми можемо насправді дозволити\(t \ge 0\)
Припустимо\(f\), є неперервним і експоненціального типу\(a\). Тоді для\(c > a\) нас є
\[f(t) = \dfrac{1}{2\pi i} \int_{c - i\infty}^{c + i\infty} F(s) e^{st}\ ds.\]
Як завжди, ця формула тримає для\(t > 0\).
- Доказ
-
Доказ використовує формулу інверсії Фур'є. Ми просто приймемо цю теорему поки що. Приклад 13.8.1 вище ілюструє теорему.
Припустимо,\(F(s)\) має кінцеве число полюсів і розпадається як\(1/s\) (або швидше). Визначте
\[f(t) = \sum \text{Res} (F(s) e^{st}, p_k), \text{ where the sum is over all the poles } p_k.\]
Тоді\(\mathcal{L} (f; s) = F(s)\)
- Доказ
-
Доказ наведено в класі. Буде додано сюди. Основні ідеї присутні в прикладах вище, хоча і вимагає досить розумного вибору контурів.
Формулу інтегральної інверсії в Рівнянні 13.8.13 можна розглядати як запис\(f(t)\) як «суму» експоненціальних чисел. Це надзвичайно корисно. Наприклад, для лінійної системи, якщо ми знаємо, як система реагує на вхід\(f(t) = e^{at}\) для всіх\(a\), то ми знаємо, як вона реагує на будь-який вхід, записуючи його як «суму» експоненціальних чисел.
