Skip to main content
LibreTexts - Ukrayinska

11.4E: Вправи

  1. Last updated
  2. Save as PDF
  • Page ID
    59829

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Практика робить досконалим

    Вправа\(\PageIndex{15}\) Graph an Ellipse with Center at the Origin

    У наступних вправах намалюйте графік кожного еліпса.

    1. \(\frac{x^{2}}{4}+\frac{y^{2}}{25}=1\)
    2. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)
    3. \(\frac{x^{2}}{25}+\frac{y^{2}}{36}=1\)
    4. \(\frac{x^{2}}{16}+\frac{y^{2}}{36}=1\)
    5. \(\frac{x^{2}}{36}+\frac{y^{2}}{16}=1\)
    6. \(\frac{x^{2}}{25}+\frac{y^{2}}{9}=1\)
    7. \(x^{2}+\frac{y^{2}}{4}=1\)
    8. \(\frac{x^{2}}{9}+y^{2}=1\)
    9. \(4 x^{2}+25 y^{2}=100\)
    10. \(16 x^{2}+9 y^{2}=144\)
    11. \(16 x^{2}+36 y^{2}=576\)
    12. \(9 x^{2}+25 y^{2}=225\)
    Відповідь

    1.

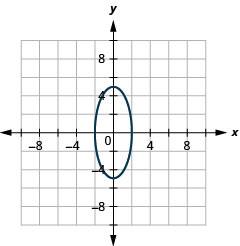
    Цей графік показує еліпс з центром (0, 0), вершинами (0, 5) та (0, від'ємним 5) та кінцевими точками другорядної осі (2, 0) та (від'ємні 2, 0).
    Малюнок 11.3.38

    3.

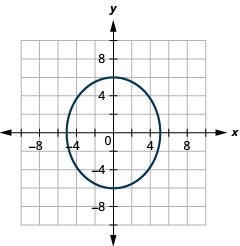
    Цей графік показує еліпс з центром (0, 0), вершинами (0, 6) та (0, від'ємним 6) та кінцевими точками другорядної осі (5, 0) та (від'ємні 5, 0).
    Малюнок 11.3.39

    5.

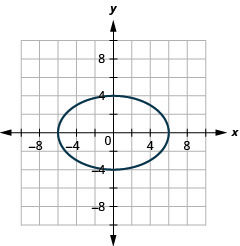
    Цей графік показує еліпс з центром (0, 0), вершинами (6, 0) та (від'ємними 6, 0) та кінцевими точками другорядної осі (0, 4) та (0, від'ємний 4).
    Малюнок 11.3.40

    7.

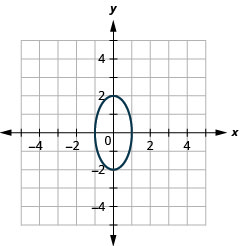
    Цей графік показує еліпс з центром (0, 0), вершинами (0, 2) та (0, від'ємним 2) та кінцевими точками другорядної осі (1, 0) та (від'ємний 1, 0).
    Малюнок 11.3.41

    9.

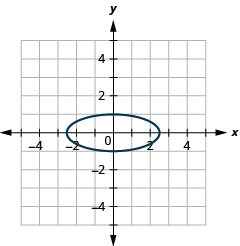
    Цей графік показує еліпс з центром (0, 0), вершинами (5, 0) та (від'ємними 5, 0) та кінцевими точками другорядної осі (0, 2) та (0, від'ємна 2).
    Малюнок 11.3.42

    11.

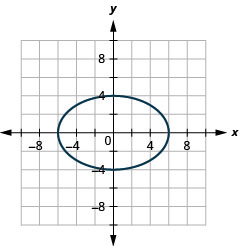
    Цей графік показує еліпс з центром (0, 0), вершинами (6, 0) та (від'ємними 6, 0) та кінцевими точками другорядної осі (0, 4) та (0, від'ємний 4).
    Малюнок 11.3.43
    Вправа\(\PageIndex{16}\) Find the Equation of an Ellipse with Center at the Origin

    У наступних вправах знайдіть рівняння еліпса, показане на графіку.

    1.

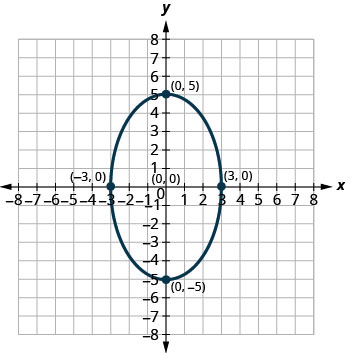
    Цей графік показує еліпс з центром (0, 0), вершинами (0, 5) та (0, від'ємним 5) та кінцевими точками другорядної осі (від'ємні 3, 0) та (3, 0).
    Малюнок 11.3.44

    2.

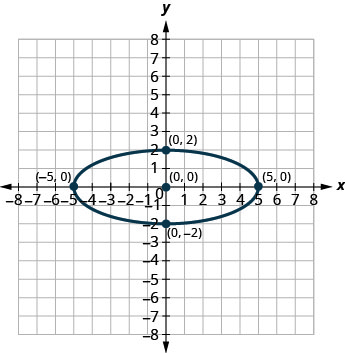
    Цей графік показує еліпс з центром (0, 0), вершинами (5, 0) та (від'ємними 5, 0) та кінцевими точками другорядної осі (0, 2) та (0, від'ємна 2).
    Малюнок 11.3.45

    3.

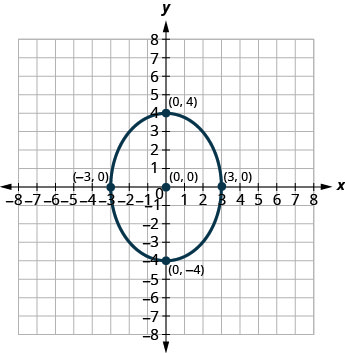
    Цей графік показує еліпс з центром (0, 0), вершинами (0, 4) та (0, від'ємним 4) та кінцевими точками другорядної осі (від'ємні 3, 0) та (3, 0).
    Малюнок 11.3.46

    4.

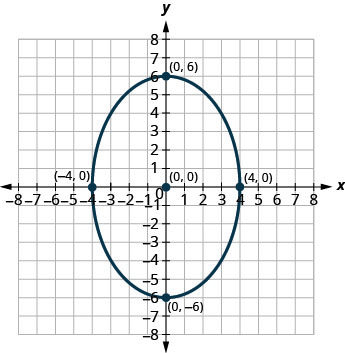
    Цей графік показує еліпс з центром (0, 0), вершинами (0, 6) та (0, від'ємним 6) та кінцевими точками другорядної осі (від'ємні 4, 0) та (4, 0).
    Малюнок 11.3.47
    Відповідь

    1. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)

    3. \(\frac{x^{2}}{9}+\frac{y^{2}}{16}=1\)

    Вправа\(\PageIndex{17}\) Graph an Ellipse with Center Not at the Origin

    У наступних вправах намалюйте графік кожного еліпса.

    1. \(\frac{(x+1)^{2}}{4}+\frac{(y+6)^{2}}{25}=1\)
    2. \(\frac{(x-3)^{2}}{25}+\frac{(y+2)^{2}}{9}=1\)
    3. \(\frac{(x+4)^{2}}{4}+\frac{(y-2)^{2}}{9}=1\)
    4. \(\frac{(x-4)^{2}}{9}+\frac{(y-1)^{2}}{16}=1\)
    Відповідь

    1.

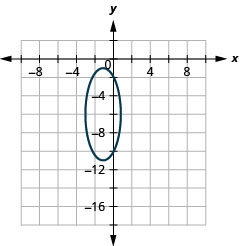
    Цей графік показує еліпс з центром (від'ємний 1, негативний 6, від'ємний 6, від'ємний 1) та (від'ємний 1, негативний 11) та кінцевими точками другорядної осі (від'ємний 3, від'ємний 6) та (1, негативний 6).
    Малюнок 11.3.48

    3.

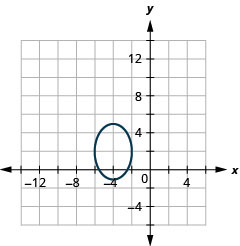
    Цей графік показує еліпс з центром (від'ємний 4, 2, вершини (від'ємний 4, 5) і (від'ємний 4, негативний 1) і кінцевими точками другорядної осі (3, 1) і (від'ємний 6, 2) і (від'ємний 2, 2).
    Малюнок 11.3.49
    Вправа\(\PageIndex{18}\) Graph an Ellipse with Center Not at the Origin

    У наступних вправах графуйте кожне рівняння шляхом перекладу.

    1. \(\frac{(x-3)^{2}}{4}+\frac{(y-7)^{2}}{25}=1\)
    2. \(\frac{(x+6)^{2}}{16}+\frac{(y+5)^{2}}{4}=1\)
    3. \(\frac{(x-5)^{2}}{9}+\frac{(y+4)^{2}}{25}=1\)
    4. \(\frac{(x+5)^{2}}{36}+\frac{(y-3)^{2}}{16}=1\)
    Відповідь

    1.

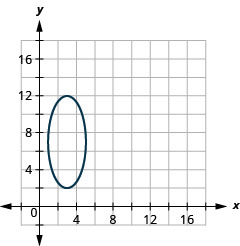
    Цей графік показує еліпс з центром (3, 7), вершинами (3, 2) та (3, 12) та кінцевими точками другорядної осі (1, 7) та (5, 7).
    Малюнок 11.3.50

    3.

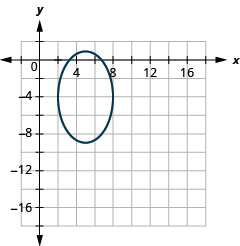
    Цей графік показує еліпс з центром (5, від'ємний 4), вершинами (5, 1) і (5, негативним 9) і кінцевими точками другорядної осі (2, від'ємний 4) і (8, негативний 4).
    Малюнок 11.3.51
    Вправа\(\PageIndex{19}\) Graph an Ellipse with Center Not at the Origin

    У наступних вправах

    1. Запишіть рівняння в стандартному вигляді і
    2. Графік.
    1. \(25 x^{2}+9 y^{2}-100 x-54 y-44=0\)
    2. \(4 x^{2}+25 y^{2}+8 x+100 y+4=0\)
    3. \(4 x^{2}+25 y^{2}-24 x-64=0\)
    4. \(9 x^{2}+4 y^{2}+56 y+160=0\)
    Відповідь

    1.

    1. \(\frac{(x-2)^{2}}{9}+\frac{(y-3)^{2}}{25}=1\)
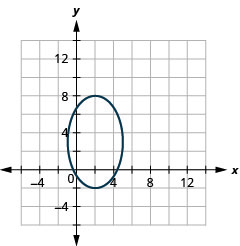
    Цей графік показує еліпс з центром (2, 3), вершинами (2, від'ємними 2) і (2, 8) і кінцевими точками другорядної осі (від'ємні 1, 3) і (5, 3).
    Малюнок 11.3.52

    3.

    1. \(\frac{y^{2}}{4}+\frac{(x-3)^{2}}{25}=1\)
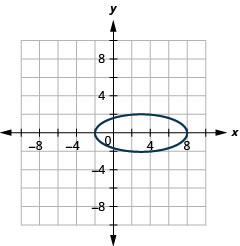
    Цей графік показує еліпс з центром (3, 0), вершинами (від'ємними 2, 0) та (8, 0) та кінцевими точками другорядної осі (3, 2) та (3, від'ємною 2).
    Малюнок 11.3.53
    Вправа\(\PageIndex{20}\) Graph an Ellipse with Center Not at the Origin

    У наступних вправах складіть графік рівняння.

    1. \(x=-2(y-1)^{2}+2\)
    2. \(x^{2}+y^{2}=49\)
    3. \((x+5)^{2}+(y+2)^{2}=4\)
    4. \(y=-x^{2}+8 x-15\)
    5. \(\frac{(x+3)^{2}}{16}+\frac{(y+1)^{2}}{4}=1\)
    6. \((x-2)^{2}+(y-3)^{2}=9\)
    7. \(\frac{x^{2}}{25}+\frac{y^{2}}{36}=1\)
    8. \(x=4(y+1)^{2}-4\)
    9. \(x^{2}+y^{2}=64\)
    10. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)
    11. \(y=6 x^{2}+2 x-1\)
    12. \(\frac{(x-2)^{2}}{9}+\frac{(y+3)^{2}}{25}=1\)
    Відповідь

    1.

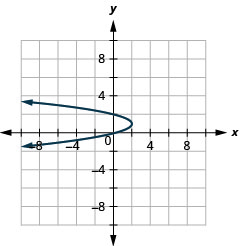
    Цей графік показує параболу з вершинами (2, 1) та y перехопленнями (0, 0) та (2, 0).
    Малюнок 11.3.54

    3.

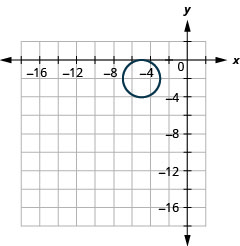
    На цьому графіку показано коло з центром (від'ємний 5, від'ємний 2) і радіусом 2 одиниці.
    Малюнок 11.3.55

    5.

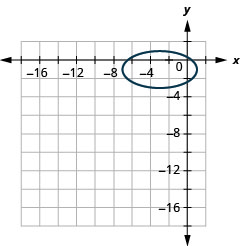
    Цей графік показує еліпс з центром (від'ємний 3, від'ємний 1), вершинами (1, від'ємний 1) і (від'ємний 7, негативний 1) і кінцевими точками другорядної осі (від'ємний 3, 1) і (негативний 3, негативний 3).
    Малюнок 11.3.56

    7.

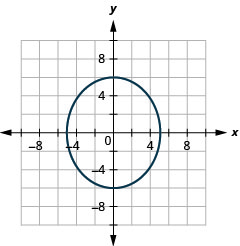
    Цей графік показує еліпс з центром (0, 0), вершинами (0, 6) та (0, від'ємним 6) та кінцевими точками другорядної осі (від'ємні 5, 0) та (5, 0).
    Малюнок 11.3.57

    9.

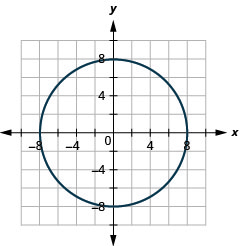
    На цьому графіку показано коло з центром (0, 0) та радіусом 8 одиниць.
    Малюнок 11.3.58

    11.

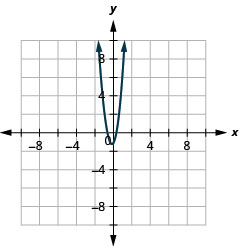
    На цьому графіку показана парабола відкриття вгору. Його вершина має значення x трохи менше 0 і значення y трохи менше мінус 1. Точка на ній знаходиться приблизно в (негативний 1, 3).
    Малюнок 11.3.59
    Вправа\(\PageIndex{21}\) Solve Application with Ellipses

    1. Планета рухається по еліптичній орбіті навколо свого сонця. Найближча планета потрапляє до Сонця приблизно\(10\) AU, а найдальша - приблизно\(30\) AU. Сонце є одним з вогнищ еліптичної орбіти. Допустивши центр еліпса у початку та маркування осей в АС, орбіта буде виглядати як на малюнку нижче. Використовуйте графік, щоб написати рівняння для еліптичної орбіти планети.

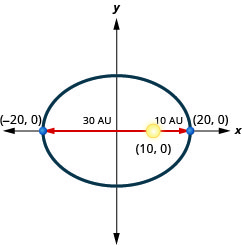
    Цей графік показує еліпс з центром (0, 0), вершинами (від'ємні 20, 0) і (20, 0). Сонце показано в точці (10, 0), яка знаходиться на 30 одиницях від лівої вершини і 10 одиниць від правої вершини.
    Малюнок 11.3.60

    2. Планета рухається по еліптичній орбіті навколо свого сонця. Найближча планета потрапляє до Сонця приблизно\(10\) AU, а найдальша - приблизно\(70\) AU. Сонце є одним з вогнищ еліптичної орбіти. Допустивши центр еліпса у початку та маркування осей в АС, орбіта буде виглядати як на малюнку нижче. Використовуйте графік, щоб написати рівняння для еліптичної орбіти планети.

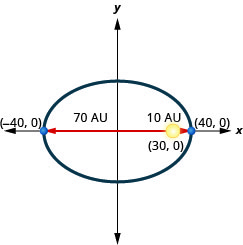
    Цей графік показує еліпс з центром (0, 0), вершинами (від'ємні 40, 0) і (40, 0). Сонце показано в точці (30, 0), яка знаходиться на 70 одиницях від лівої вершини і 10 одиниць від правої вершини.
    Малюнок 11.3.61

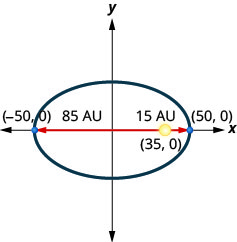
    3. Комета рухається по еліптичній орбіті навколо Сонця. Найближча комета потрапляє до сонця приблизно\(15\) AU, а найдальша - приблизно\(85\) AU. Сонце є одним з вогнищ еліптичної орбіти. Допустивши центр еліпса у початку та маркування осей в АС, орбіта буде виглядати як на малюнку нижче. Використовуйте графік, щоб написати рівняння для еліптичної орбіти комети.

    Цей графік показує еліпс з центром (0, 0), вершинами (від'ємні 50, 0) і (50, 0). Сонце показано в точці (35, 0), яка становить 85 одиниць від лівої вершини і 15 одиниць від правої вершини.
    Малюнок 11.3.62

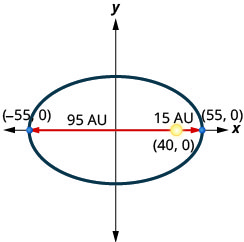
    4. Комета рухається по еліптичній орбіті навколо Сонця. Найближча комета потрапляє до сонця приблизно\(15\) AU, а найдальша - приблизно\(95\) AU. Сонце є одним з вогнищ еліптичної орбіти. Допустивши центр еліпса у початку та маркування осей в АС, орбіта буде виглядати як на малюнку нижче. Використовуйте графік, щоб написати рівняння для еліптичної орбіти комети.

    Цей графік показує еліпс з центром (0, 0), вершинами (від'ємні 55, 0) і (55, 0). Сонце показано в точці (40, 0), яка становить 95 одиниць від лівої вершини і 15 одиниць від правої вершини.
    Малюнок 11.3.63
    Відповідь

    1. \(\frac{x^{2}}{400}+\frac{y^{2}}{300}=1\)

    3. \(\frac{x^{2}}{2500}+\frac{y^{2}}{1275}=1\)

    Вправа\(\PageIndex{22}\) Writing Exercises
    1. Своїми словами, визначте еліпс і запишіть рівняння еліпса, центрованого на початку, в стандартній формі. Намалюйте ескіз еліпса, який позначає центр, вершини та великі та малі осі.
    2. Поясніть своїми словами, як отримати осі з рівняння в стандартному вигляді.
    3. Порівняйте і порівняйте графіки рівнянь\(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\) і\(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\).
    4. Поясніть своїми словами різницю між вершиною і фокусом еліпса.
    Відповідь

    1. Відповіді можуть відрізнятися

    3. Відповіді можуть відрізнятися

    Самостійна перевірка

    а Після виконання вправ скористайтеся цим контрольним списком, щоб оцінити своє володіння цілями цього розділу.

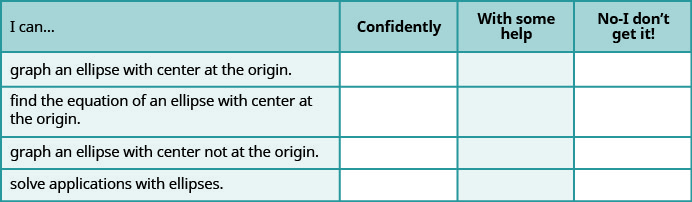
    Ця таблиця має 4 стовпці 4 рядки і рядок заголовка. Рядок заголовка позначає кожен стовпець, який я можу, впевнено, з деякою допомогою і ні, я роблю €™ т отримати його. Перші стовпці мають такі твердження: графуйте еліпс з центром у початку, знайдіть рівняння еліпса з центром у початку, графуйте еліпс з центром не у початку, вирішуйте додатки з еліпсами. Решта стовпці порожні.
    Малюнок 11.3.64

    б Що говорить вам цей контрольний список про ваше володіння цим розділом? Які кроки ви зробите для вдосконалення?