11.3: Параболи

Цілі навчання

До кінця цього розділу ви зможете:

• Графік вертикальних парабол
• Графік горизонтальних парабол
• Вирішуйте програми за допомогою парабол

Будьте готові

Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

1. Графік:$y=-3 x^{2}+12 x-12$.
   Якщо ви пропустили цю проблему, перегляньте приклад 9.47.
2. Вирішіть, заповнивши квадрат:$x^{2}-6 x+6=0$.
   Якщо ви пропустили цю проблему, перегляньте приклад 9.12.
3. Пишіть в стандартному вигляді:$y=3 x^{2}-6 x+5$.
   Якщо ви пропустили цю проблему, перегляньте приклад 9.59.

Графік вертикальних парабол

Наступний конічний розділ, який ми розглянемо, - парабола. Ми визначаємо параболу як усі точки на площині, які знаходяться на однаковій відстані від фіксованої точки та фіксованої лінії. Фіксована точка називається фокусом, а нерухома - директриса параболи.

Малюнок 11.2.1

Визначення$\PageIndex{1}$: Parabola, Focus, and Directrix

Парабола - це всі точки в площині, які знаходяться на однаковій відстані від фіксованої точки і фіксованої лінії. Фіксована точка називається фокусом, а нерухома - директриса параболи.

Малюнок 11.2.2

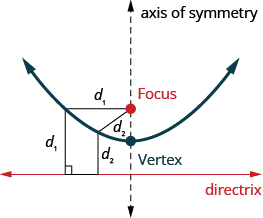
Раніше ми навчилися графувати вертикальні параболи із загальної форми або стандартної форми за допомогою властивостей. Ці методи також будуть працювати тут. Тут ми підсумуємо властивості.

Вертикальні параболи

Таблиця 11.2.1

	Загальна форма $y=a x^{2}+b x+c$	Стандартна форма $y=a(x-h)^{2}+k$
Орієнтація	\ (y=a x^ {2} +b x+c\) ">$a>0$ вгору;$a<0$ вниз	\ (y=a (x-h) ^ {2} +k\) ">$a>0$ вгору;$a<0$ вниз
Вісь симетрії	\ (y=a x^ {2} +б х+с\) ">$x=-\dfrac{b}{2 a}$	\ (y=a (x-h) ^ {2} +k\) ">$x=h$
Вершина	\ (y=a x^ {2} +b x+c\) ">Замінити$x=-\dfrac{b}{2 a}$ і вирішити для$y .$	\ (y=a (x-h) ^ {2} +k\) ">$(h, k)$
$y$-перехопити	\ (y=a x ^ {2} +б х+с\) ">Нехай$x=0$	\ (y=a (x-h) ^ {2} +k\) ">Нехай$x=0$
$x$-перехоплює	\ (y=a x ^ {2} +б х+с\) ">Нехай$y=0$	\ (y=a (x-h) ^ {2} +k\) ">Нехай$y=0$

Графіки показують, як виглядають параболи, коли вони відкриваються вгору або вниз. Їх положення по відношенню до$x$ - або$y$ -осі є лише прикладом.

Малюнок 11.2.3

Щоб скласти графік параболи з цих форм, ми використовували наступні кроки.

Графік вертикальних парабол

Як графувати вертикальні параболи$y=a x^{2}+b x+c$ або$f(x)=a(x-h)^{2}+k$ за допомогою властивостей.

• Крок 1: Визначте, чи відкривається парабола вгору або вниз.
• Крок 2. Знайдіть вісь симетрії.
• Крок 3. Знайдіть вершину.
• Крок 4. Знайти$y$ -перехоплення. Знайти точку, симетричну до$y$ -перехоплення поперек осі симетрії.
• Крок 5. Знайдіть$x$ -перехоплення.
• Крок 6. Графік параболи.

У наступному прикладі розглядається метод побудови графіка параболи із загальної форми її рівняння.

Приклад$\PageIndex{1}$

Графік$y=-x^{2}+6 x-8$ за допомогою властивостей.

Рішення:

Таблиця 11.2.2

	$\begin{align*} \color{red}{y} &\color{red}{=} a x^{2}+b x+c \\[4pt]  \color{black}{y} &=-x^{2}+6 x-8 \end{align*}$
Так як$a$ є$-1$, парабола відкривається вниз.
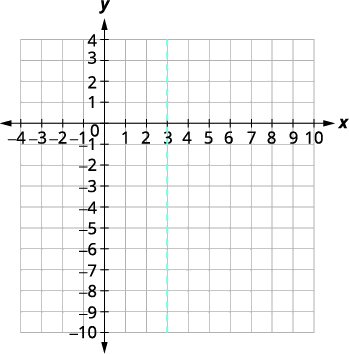
Щоб знайти вісь симетрії, знайдіть$x=-\dfrac{b}{2 a}$.	$\begin{align*} x &=-\dfrac{b}{2 a}\\[4pt] x &=-\dfrac{6}{2(-1)} \\[4pt] x &= 3 \end{align*}$
	Вісь симетрії є$x=3$.
Вершина знаходиться на лінії$x=3$.	$y=-x^{2}+6 x-8$
Нехай$x=3$.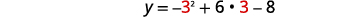
	$\begin{align*} y &=-9+18-8 \\[4pt] y &=1 \end{align*}$
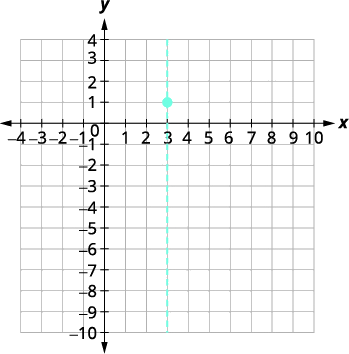
	Вершина є$(3,1)$.
$y$-Перехоплення відбувається, коли$x=0$.	$y=-x^{2}+6 x-8$
Замінник$x=0$.	$y=-\color{red}{0}^{\color{black}{2}}+6 \cdot \color{red}{0} \color{black}{-} 8$
Спростити.	$y=-8$
	$y$-Перехоплення є$(0,-8)$.
Точка$(0,−8)$ - три одиниці зліва від лінії симетрії. Точка три одиниці праворуч від лінії симетрії є$(6,−8)$.	Точка симетрична до$y$ -перехоплення є$(6,−8)$.
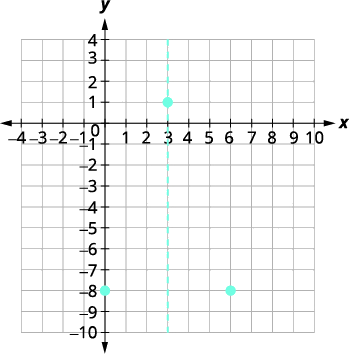$x$-Перехоплення відбувається, коли$y=0$.	$y=-x^{2}+6 x-8$
Нехай$y=0$.	$\color{red}{0} \color{black}{=}-x^{2}+6 x-8$
Фактор GCF.	$0=-\left(x^{2}-6 x+8\right)$
Фактор триноміалу.	$0=-(x-4)(x-2)$
Вирішити для$x$.	$x=4, \quad x=2$
	$x$-перехоплює є$(4,0),(2,0)$.
Графік параболи.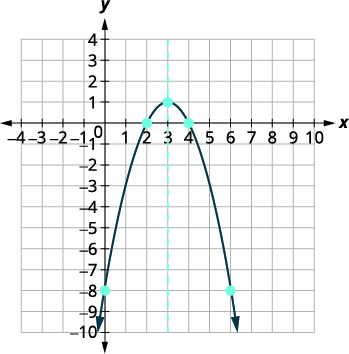

Вправа$\PageIndex{1}$

Графік$y=-x^{2}+5 x-6$ за допомогою властивостей.

Відповідь

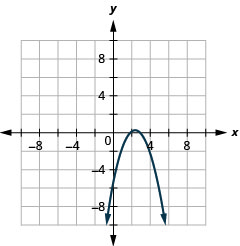
Малюнок 11.2.24

Вправа$\PageIndex{2}$

Графік$y=-x^{2}+8 x-12$ за допомогою властивостей.

Відповідь

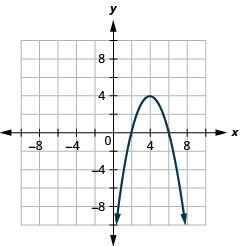
Малюнок 11.2.25

У наступному прикладі розглядається метод побудови графіка параболи зі стандартної форми її рівняння,$y=a(x-h)^{2}+k$.

Приклад$\PageIndex{2}$

Напишіть$y=3 x^{2}-6 x+5$ у стандартній формі, а потім використовуйте властивості стандартної форми для побудови графіка рівняння.

Рішення:

Таблиця 11.2.3

Перепишіть функцію в$y=a(x-h)^{2}+k$ форму, заповнивши квадрат.	$\begin{align*} y &=3 x^{2}-6 x+5 \\[4pt] y &=3\left(x^{2}-2 x\right)+5 \\[4pt] y &=3\left(x^{2}-2 x+1\right) + 5-3  \\[4pt] y &=3(x-1)^{2}+2 \end{align*}$
Визначте константи$a, h, k$.	$a=3, h=1, k=2$
З тих пір$a=2$, парабола відкривається вгору.
Вісь симетрії є$x=h$.	Вісь симетрії є$x=1$.
Вершина є$(h,k)$.	Вершина є$(1,2)$.
Знайти$y$ -перехоплення шляхом підстановки$x=0$,	$\begin{align*} y &=3(x-1)^{2}+2 \\[4pt] y &=3 \cdot 0^{2}-6 \cdot 0+5 \\[4pt] y &=0 \end{align*}$
	$y$-перехопити$(0,5)$
Знайдіть точку, симетричну$(0,5)$ поперек осі симетрії.	$(2,5)$
Знайдіть$x$ -перехоплення.	$\begin{aligned} y &=3(x-1)^{2}+2 \\[4pt] 0 &=3(x-1)^{2}+2 \\[4pt] -2 &=3(x-1)^{2} \\[4pt] -\dfrac{2}{3} &=(x-1)^{2} \\[4pt] \pm \sqrt{-\dfrac{2}{3}} &=x-1 \end{aligned}$
	Квадратний корінь від'ємного числа говорить нам, що розв'язки є комплексними числами. Так що немає$x$ -перехоплень.
Графік параболи.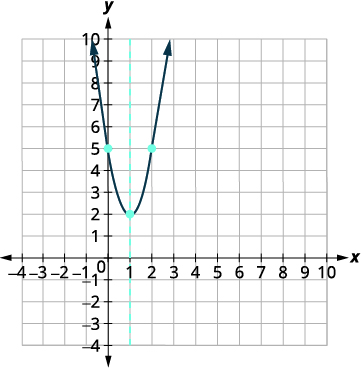

Вправа$\PageIndex{3}$

1. Пишіть$y=2 x^{2}+4 x+5$ в стандартній формі і
2. використовувати властивості стандартної форми для графування рівняння.

Відповідь

1. $y=2(x+1)^{2}+3$
2.  

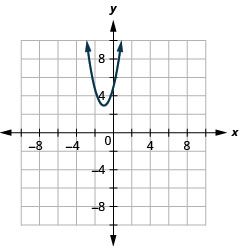
Малюнок 11.2.28

Вправа$\PageIndex{4}$

1. Пишіть$y=-2 x^{2}+8 x-7$ в стандартній формі і
2. використовувати властивості стандартної форми для графування рівняння.

Відповідь

1. $y=-2(x-2)^{2}+1$
2.  

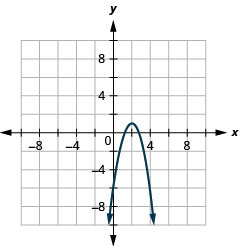
Малюнок 11.2.29

Графік горизонтальних парабол

Наша робота поки займалася лише параболами, які відкриваються вгору або вниз. Зараз ми розглянемо горизонтальні параболи. Ці параболи відкриваються або ліворуч, або праворуч. Якщо ми поміняємо$x$ і$y$ в наших попередніх рівняннях для парабол, ми отримаємо рівняння для парабол, які відкриваються ліворуч або праворуч.

Горизонтальні параболи

Таблиця 11.2.4

	Загальна форма $x=a y^{2}+b y+c$	Стандартна форма $x=a(y-k)^{2}+h$
Орієнтація	\ (x = a y^ {2} +b y+c\) ">$a>0$ праворуч;$a<0$ ліворуч	\ (x=a (y-k) ^ {2} +h\) ">$a>0$ праворуч;$a<0$ ліворуч
Вісь симетрії	\ (x=a y^ {2} +b y+c\) ">$y=-\dfrac{b}{2 a}$	\ (x=a (y-k) ^ {2} +h\) ">$y=k$
Вершина	\ (x=a y^ {2} +b y+c\) ">Замінити$y=-\dfrac{b}{2 a}$ і вирішити для$x .$	\ (x=a (y-k) ^ {2} +h\) ">$(h, k)$
$x$-перехоплює	\ (x = a y^ {2} +b y+c\) ">Нехай$x=0$	\ (x=a (y-k) ^ {2} +h\) ">Нехай$x=0$
$y$-перехопити	\ (x = a y^ {2} +b y+c\) ">Нехай$y=0$	\ (x=a (y-k) ^ {2} +h\) ">Нехай$y=0$

Графіки показують, як виглядають параболи, коли вони ліворуч або праворуч. Їх положення по відношенню до$x$ - або$y$ -осі є лише прикладом.

Малюнок 11.2.30

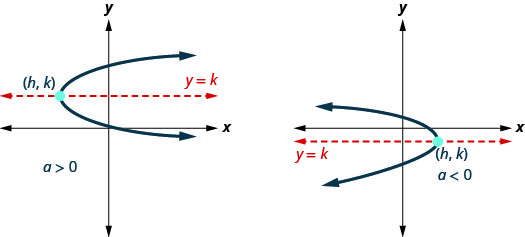
Дивлячись на ці параболи, чи представляють їх графіки функцію? Оскільки обидва графіки не пройдуть тест вертикальної лінії, вони не представляють функцію.

Графік параболи, яка відкривається ліворуч або праворуч, в основному те саме, що ми зробили для парабол, які відкриваються вгору або вниз, з розворотом$y$ змінних$x$ і.

Howto: Графік горизонтальних парабол$y=a x^{2}+b x+c$ or $f(x)=a(x-h)^{2}+k$ using Properties

• Крок 1: Визначте, чи відкривається парабола ліворуч або праворуч.
• Крок 2: Знайдіть вісь симетрії.
• Крок 3: Знайдіть вершину.
• Крок 4: Знайдіть$x$ -перехоплення. Знайти точку, симетричну до$x$ -перехоплення поперек осі симетрії.
• Крок 5: Знайдіть$y$ -перехоплення.
• Крок 6: Графік параболи.

Приклад$\PageIndex{3}$

Графік$x=2 y^{2}$ за допомогою властивостей.

Рішення:

Таблиця 11.2.5

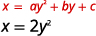З тих пір$a=2$, парабола відкривається праворуч.
Щоб знайти вісь симетрії, знайдіть$y=-\dfrac{b}{2 a}$	$y=-\dfrac{b}{2 a}$
	$y=-\dfrac{0}{2(2)}$
	$y=0$
	Вісь симетрії є$y=0$.
Вершина знаходиться на лінії$y=0$.	$x=2 y^{2}$
Нехай$y=0$.
	$x=0$
	Вершина є$(0,0)$.

Оскільки вершина є$(0,0)$, то обидва$x$ - і$y$ -перехоплення є точкою$(0,0)$. Для графіка параболи нам потрібно більше очок. В цьому випадку найпростіше вибрати значення$y$.

Малюнок 11.2.38

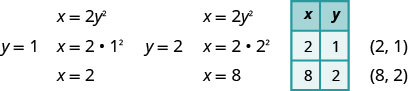
Ми також будуємо точки, симетричні$(2,1)$ і$(8,2)$ поперек$y$ -осі, точки$(2,−1),(8,−2)$.

Графік параболи.

Малюнок 11.2.39

Вправа$\PageIndex{5}$

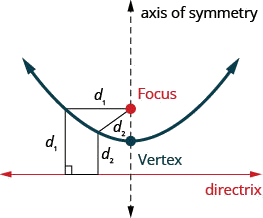
Графік$x=y^{2}$ за допомогою властивостей.

Відповідь

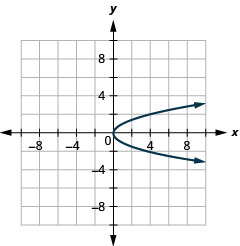
Малюнок 11.2.40

Вправа$\PageIndex{6}$

Графік$x=-y^{2}$ за допомогою властивостей.

Відповідь

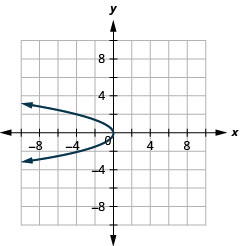
Малюнок 11.2.41

У наступному прикладі вершина не є початком.

Приклад$\PageIndex{4}$

Графік$x=-y^{2}+2 y+8$ за допомогою властивостей.

Рішення:

Таблиця 11.2.6

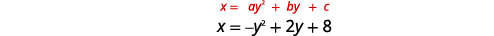Так як$a=-1$ парабола відкривається вліво.
Щоб знайти вісь симетрії, знайдіть$y=-\dfrac{b}{2 a}$	$y=-\dfrac{b}{2 a}$
	$y=-\dfrac{2}{2(-1)}$
	$y=1$
	Вісь симетрії є$y=1$.
Вершина знаходиться на лінії$y=1$.	$x=-y^{2}+2 y+8$
Нехай$y=1$.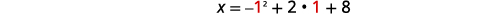
	$x=9$
	Вершина є$(9,1)$.
$x$-Перехоплення відбувається, коли$y=0$.	$x=-y^{2}+2 y+8$
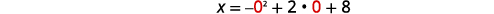	$x=8$
	$x$-Перехоплення є$(8,0)$.
Точка$(8,0)$ знаходиться на одну одиницю нижче лінії симетрії. Симетрична точка на одиницю над лінією симетрії$(8,2)$	Симетрична точка є$(8,2)$.
$y$-Перехоплення відбувається, коли$x=0$.	$x=-y^{2}+2 y+8$
Замінник$x=0$.	$0=-y^{2}+2 y+8$
Вирішити.	$y^{2}-2 y-8=0$
	$(y-4)(y+2)=0$
	$y=4, \quad  y=-2$
	$y$-перехоплює є$(0,4)$ і$(0,-2)$.
З'єднайте точки для графіка параболи.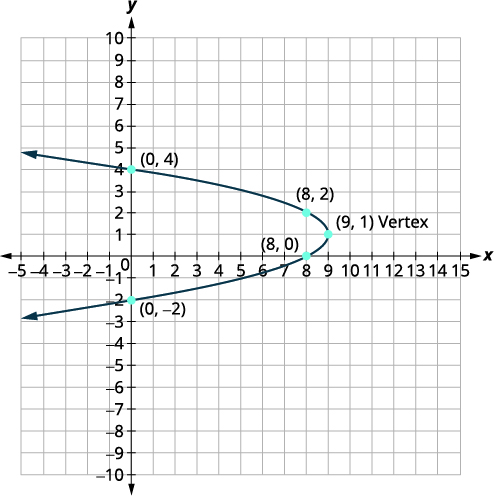

Вправа$\PageIndex{7}$

Графік$x=-y^{2}-4 y+12$ за допомогою властивостей.

Відповідь

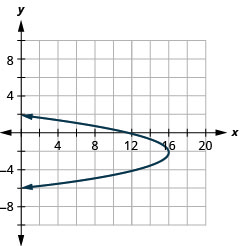
Малюнок 11.2.58

Вправа$\PageIndex{8}$

Графік$x=-y^{2}+2 y-3$ за допомогою властивостей.

Відповідь

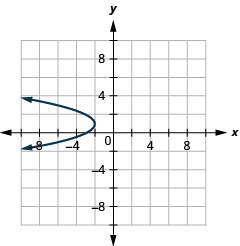
Малюнок 11.2.59

У таблиці 11.2.4 ми бачимо зв'язок між рівнянням в стандартному вигляді і властивостями параболи. У полі Як перелічити кроки для побудови параболи в стандартній формі$x=a(y-k)^{2}+h$. Цю процедуру ми будемо використовувати в наступному прикладі.

Приклад$\PageIndex{5}$

Графік$x=2(y-2)^{2}+1$ з використанням властивостей.

Рішення:

Таблиця 11.2.7

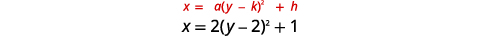Визначте константи$a, h, k$.	$a=2, h=1, k=2$
З тих пір$a=2$, парабола відкривається праворуч.
Вісь симетрії є$y=k$.	Вісь симетрії є$y=2$.
Вершина є$(h,k)$.	Вершина є$(1,2)$.
Знайти$x$ -intercept шляхом підстановки$y=0$.	$x=2(y-2)^{2}+1$ $x=2(0-2)^{2}+1$ $x=9$
	$x$-Перехоплення є$(9,0)$.
Знайдіть точку, симетричну$(9,0)$ поперек осі симетрії.	$(9,4)$
Знайдіть$y$ -перехоплення. Нехай$x=0$.	$\begin{aligned} x &=2(y-2)^{2}+1 \\ 0 &=2(y-2)^{2}+1 \\-1 &=2(y-2)^{2} \end{aligned}$
	Квадрат не може бути негативним, тому реального рішення не існує. Так що немає$y$ -перехоплень.
Графік параболи.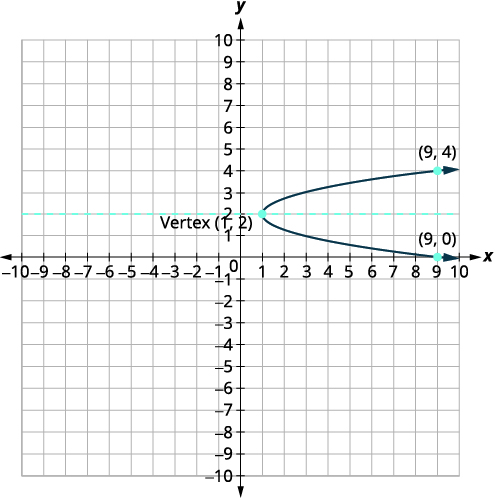

Вправа$\PageIndex{9}$

Графік$x=3(y-1)^{2}+2$ з використанням властивостей.

Відповідь

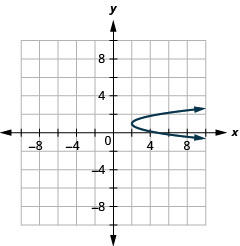
Малюнок 11.2.63

Вправа$\PageIndex{10}$

Графік$x=2(y-3)^{2}+2$ з використанням властивостей.

Відповідь

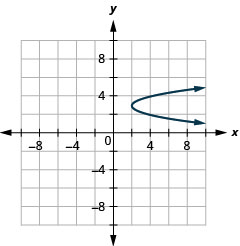
Малюнок 11.2.64

У наступному прикладі ми помічаємо, що a є негативним, і тому парабола відкривається ліворуч.

Приклад$\PageIndex{6}$

Графік$x=-4(y+1)^{2}+4$ з використанням властивостей.

Рішення:

Таблиця 11.2.8

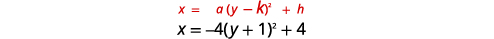Визначте константи$a, h, k$.	$a=-4, h=4, k=-1$
Так як$a=-4$ парабола відкривається вліво.
Вісь симетрії є$y=k$.	Вісь симетрії є$y=-1$.
Вершина є$(h,k)$.	Вершина є$(4,-1)$.
Знайти$x$ -intercept шляхом підстановки$y=0$.	$x=-4(y+1)^{2}+4$ $x=-4(0+1)^{2}+4$ $x=0$
	$x$-Перехоплення є$(0,0)$.
Знайдіть точку, симетричну$(0,0)$ поперек осі симетрії.	$(0,-2)$
Знайдіть$y$ -перехоплення.	$x=-4(y+1)^{2}+4$
Нехай$x=0$.	$\begin{aligned} 0 &=-4(y+1)^{2}+4 \\-4 &=-4(y+1)^{2} \\ 1 &=(y+1)^{2} \\ y+1 &=\pm 1 \end{aligned}$
	$y=-1+1 \quad y=-1-1$
	$y=0 \quad\quad y=-2$
	$y$-перехоплює є$(0,0)$ і$(0,-2)$.
Графік параболи.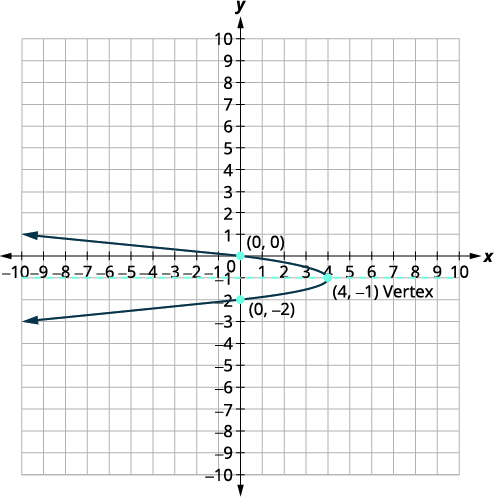

Вправа$\PageIndex{11}$

Графік$x=-4(y+2)^{2}+4$ з використанням властивостей.

Відповідь

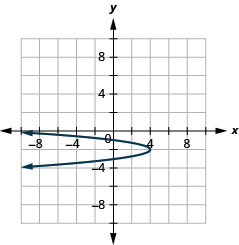
Малюнок 11.2.68

Вправа$\PageIndex{12}$

Графік$x=-2(y+3)^{2}+2$ з використанням властивостей.

Відповідь

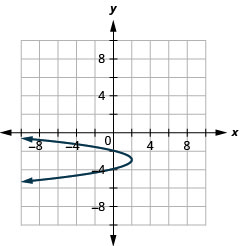
Малюнок 11.2.69

Наступний приклад вимагає спочатку поставити рівняння в стандартному вигляді, а потім використовувати властивості.

Приклад$\PageIndex{7}$

Напишіть$x=2 y^{2}+12 y+17$ у стандартній формі, а потім використовуйте властивості стандартної форми для побудови графіка рівняння.

Рішення:

Таблиця 11.2.9

	$x=2 y^{2}+12 y+17$
Перепишіть функцію в$x=a(y-k)^{2}+h$ форму, заповнивши квадрат.	$x=2\left(y^{2}+6 y\right)+17$
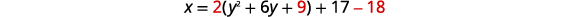	$x=2(y+3)^{2}-1$
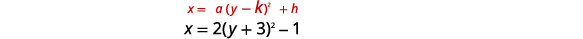Визначте константи$a, h, k$.	$a=2, h=-1, k=-3$
З тих пір$a=2$, парабола відкривається праворуч.
Вісь симетрії є$y=k$.	Вісь симетрії є$y=-3$.
Вершина є$(h,k)$.	Вершина є$(-1,-3)$.
Знайти$x$ -intercept шляхом підстановки$y=0$.	$x=2(y+3)^{2}-1$ $x=2(0+3)^{2}-1$ $x=17$
	$x$-Перехоплення є$(17,0)$.
Знайдіть точку, симетричну$(17,0)$ поперек осі симетрії.	$(17,-6)$
Знайдіть$y$ -перехоплення. Нехай$x=0$.	$\begin{aligned} x &=2(y+3)^{2}-1 \\ 0 &=2(y+3)^{2}-1 \\ 1 &=2(y+3)^{2} \\ \dfrac{1}{2} &=(y+3)^{2} \\ y+3 &=\pm \sqrt{\dfrac{1}{2}} \\ y &=-3 \pm \dfrac{\sqrt{2}}{2} \end{aligned}$
	$y=-3+\dfrac{\sqrt{2}}{2} \quad y=-3-\dfrac{\sqrt{2}}{2}$
	$y \approx-2.3 \quad y \approx-3.7$
	$y$-перехоплює є$\left(0,-3+\dfrac{\sqrt{2}}{2}\right),\left(0,-3-\dfrac{\sqrt{2}}{2}\right)$.
Графік параболи.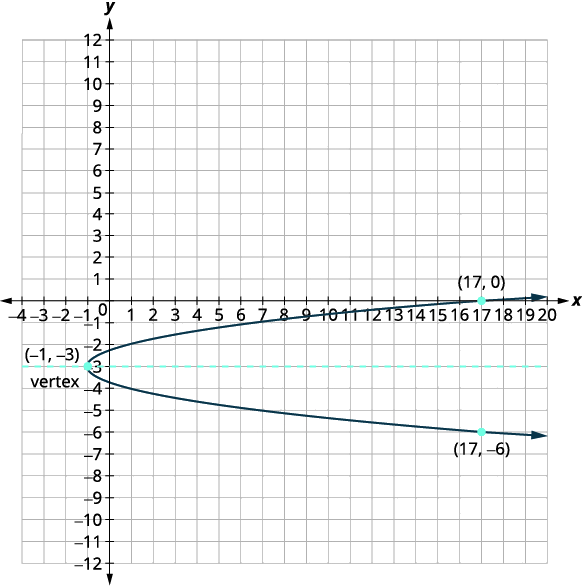

Вправа$\PageIndex{13}$

1. Пишіть$x=3 y^{2}+6 y+7$ в стандартній формі і
2. Використовуйте властивості стандартної форми для побудови графіка рівняння.

Відповідь

1. $x=3(y+1)^{2}+4$
2.  

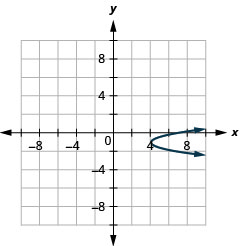
Малюнок 11.2.77

Вправа$\PageIndex{14}$

1. Пишіть$x=-4 y^{2}-16 y-12$ в стандартній формі і
2. Використовуйте властивості стандартної форми для побудови графіка рівняння.

Відповідь

1. $x=-4(y+2)^{2}+4$
2.  

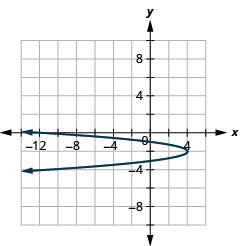
Малюнок 11.2.78

Вирішуйте програми за допомогою Parabolas

Багато архітектурних конструкцій містять параболи. Нерідкі випадки, коли мости будуються з використанням парабол, як ми побачимо в наступному прикладі.

Приклад$\PageIndex{8}$

Знайдіть рівняння параболічної арки, утвореної в фундаменті показаного моста. Запишіть рівняння в стандартному вигляді.

Малюнок 11.2.79

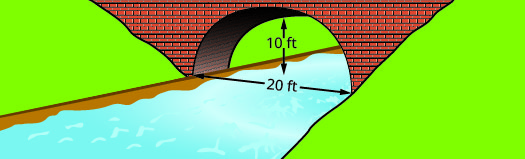
Рішення:

Спочатку ми встановимо систему координат і намалюємо параболу. Графік дасть нам інформацію, необхідну нам для написання рівняння графа в стандартному вигляді$y=a(x-h)^{2}+k$.

Таблиця 11.2.10

Нехай нижня ліва сторона моста буде початком координатної сітки в точці$(0,0)$. Оскільки основа є шириною$20$ стопи, точка$(20,0)$ представляє нижню праву сторону. Міст висотою 10 футів у найвищій точці. Найвища точка - це вершина параболи, тому$y$ координата вершини буде$10$. Оскільки міст симетричний, вершина повинна опускатися на півдорозі між крайньою лівою точкою$(0,0)$, і крайньою правою точкою$(20,0)$. З цього ми знаємо, що$x$ -координата вершини також буде$10$.
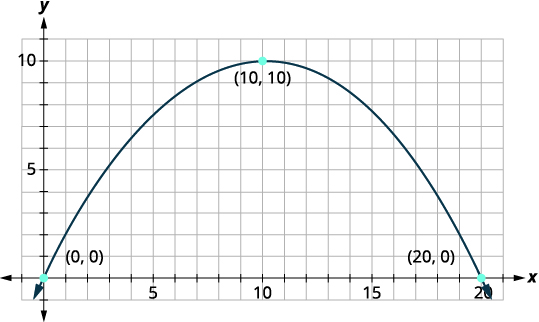Визначте вершину,$(h,k)$.	$(h, k)=(10,10)$
	$h=10, \quad k=10$
Підставте значення в стандартну форму. Значення до$a$ сих пір невідомо. Для знаходження значення$a$ використовують один з інших пунктів на параболі.	$\begin{aligned} y &=a(x-h)^{2}+k \\ y &=a(x-10)^{2}+10 \\(x, y) &=(0,0) \end{aligned}$
Підставте значення іншої точки в рівняння.	$y=a(x-10)^{2}+10$ $0=a(0-10)^{2}+10$
Вирішити для$a$.	$\begin{aligned} 0 &=a(0-10)^{2}+10 \\-10 &=a(-10)^{2} \\-10 &=100 a \\ \dfrac{-10}{100} &=a \\ a &=-\dfrac{1}{10} \end{aligned}$
	$y=a(x-10)^{2}+10$
Підставте значення для$a$ в рівняння.	$y=-\dfrac{1}{10}(x-10)^{2}+10$

Вправа$\PageIndex{15}$

Знайдіть рівняння параболічної арки, утвореної в фундаменті показаного моста. Запишіть рівняння в стандартному вигляді.

Малюнок 11.2.81

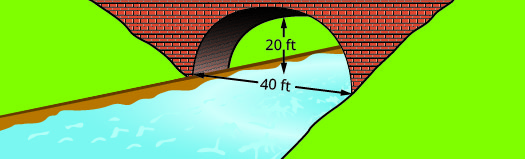
Відповідь

$y=-\dfrac{1}{20}(x-20)^{2}+20$

Вправа$\PageIndex{16}$

Знайдіть рівняння параболічної арки, утвореної в фундаменті показаного моста. Запишіть рівняння в стандартному вигляді.

Малюнок 11.2.82

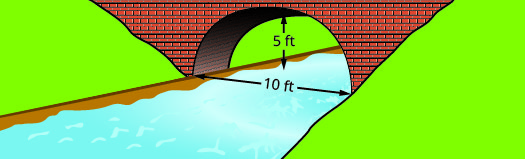
Відповідь

$y=-\dfrac{1}{5} x^{2}+2 x y=-\dfrac{1}{5}(x-5)^{2}+5$

Отримайте доступ до цих онлайн-ресурсів для отримання додаткових інструкцій та практики з квадратичними функціями та параболами.

• Квадратичні функції
• Вступ до конічних та графічних горизонтальних парабол

Ключові концепції

• Парабола: Парабола - це всі точки на площині, які знаходяться на однаковій відстані від фіксованої точки та фіксованої лінії. Фіксована точка називається фокусом, а нерухома - директриса параболи.

Вертикальні параболи

Таблиця 11.2.1

	Загальна форма $y=a x^{2}+b x+c$	Стандартна форма $y=a(x-h)^{2}+k$
Орієнтація	\ (y=a x^ {2} +b x+c\) ">$a>0$ вгору;$a<0$ вниз	\ (y=a (x-h) ^ {2} +k\) ">$a>0$ вгору;$a<0$ вниз
Вісь симетрії	\ (y=a x^ {2} +б х+с\) ">$x=-\dfrac{b}{2 a}$	\ (y=a (x-h) ^ {2} +k\) ">$x=h$
Вершина	\ (y=a x^ {2} +b x+c\) ">Замінити$x=-\dfrac{b}{2 a}$ і вирішити для$y .$	\ (y=a (x-h) ^ {2} +k\) ">$(h, k)$
$y$-перехопити	\ (y=a x ^ {2} +б х+с\) ">Нехай$x=0$	\ (y=a (x-h) ^ {2} +k\) ">Нехай$x=0$
$x$-перехоплює	\ (y=a x ^ {2} +б х+с\) ">Нехай$y=0$	\ (y=a (x-h) ^ {2} +k\) ">Нехай$y=0$

Малюнок 11.2.3

• Як графувати вертикальні параболи$y=a x^{2}+b x+c$ або$f(x)=a(x-h)^{2}+k)$ за допомогою властивостей.

1. Визначте, чи відкривається парабола вгору або вниз.
2. Знайдіть вісь симетрії.
3. Знайдіть вершину.
4. Знайти$y$ -перехоплення. Знайти точку, симетричну до$y$ -перехоплення поперек осі симетрії.
5. Знайдіть$x$ -перехоплення.
6. Графік параболи.

Горизонтальні параболи

Таблиця 11.2.4

	Загальна форма $x=a y^{2}+b y+c$	Стандартна форма $x=a(y-k)^{2}+h$
Орієнтація	\ (x = a y^ {2} +b y+c\) ">$a>0$ праворуч;$a<0$ ліворуч	\ (x=a (y-k) ^ {2} +h\) ">$a>0$ праворуч;$a<0$ ліворуч
Вісь симетрії	\ (x=a y^ {2} +b y+c\) ">$y=-\dfrac{b}{2 a}$	\ (x=a (y-k) ^ {2} +h\) ">$y=k$
Вершина	\ (x=a y^ {2} +b y+c\) ">Замінити$y=-\dfrac{b}{2 a}$ і вирішити для$x .$	\ (x=a (y-k) ^ {2} +h\) ">$(h, k)$
$x$-перехоплює	\ (x = a y^ {2} +b y+c\) ">Нехай$x=0$	\ (x=a (y-k) ^ {2} +h\) ">Нехай$x=0$
$y$-перехопити	\ (x = a y^ {2} +b y+c\) ">Нехай$y=0$	\ (x=a (y-k) ^ {2} +h\) ">Нехай$y=0$

Малюнок 11.2.30

Графік горизонтальних парабол

Як графувати горизонтальні параболи$x=a y^{2}+b y+c$ або$x=a(y-k)^{2}+h$ за допомогою властивостей.

1. Визначте, чи відкривається парабола ліворуч або праворуч.
2. Знайдіть вісь симетрії.
3. Знайдіть вершину.
4. Знайти$x$ -перехоплення. Знайти точку, симетричну до$x$ -перехоплення поперек осі симетрії.
5. Знайдіть$y$ -перехоплення.
6. Графік параболи.

Глосарій

парабола

Парабола - це всі точки в площині, які знаходяться на однаковій відстані від фіксованої точки і фіксованої лінії.