Skip to main content
LibreTexts - Ukrayinska

Глава 11 Огляд вправ

  1. Last updated
  2. Save as PDF
  • Page ID
    59809

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Розділ Огляд Вправи

    Формули відстані та середини; Кола

    Вправа\(\PageIndex{1}\) Use the Distance Formula

    У наступних вправах знайдіть відстань між точками. Округляйте до найближчої десятої, якщо потрібно.

    1. \((-5,1)\)і\((-1,4)\)
    2. \((-2,5)\)і\((1,5)\)
    3. \((8,2)\)і\((-7,-3)\)
    4. \((1,-4)\)і\((5,-5)\)
    Відповідь

    2. \(d=3\)

    4. \(d=\sqrt{17}, d \approx 4.1\)

    Вправа\(\PageIndex{2}\) Use the Midpoint Formula

    У наступних вправах знайдіть середину відрізків лінії, кінцеві точки яких задані.

    1. \((-2,-6)\)і\((-4,-2)\)
    2. \((3,7)\)і\((5,1)\)
    3. \((-8,-10)\)і\((9,5)\)
    4. \((-3,2)\)і\((6,-9)\)
    Відповідь

    2. \((4,4)\)

    4. \(\left(\frac{3}{2},-\frac{7}{2}\right)\)

    Вправа\(\PageIndex{3}\) Write the Equation of a Circle in Standard Form

    У наступних вправах запишіть стандартну форму рівняння кола з заданою інформацією.

    1. радіус є\(15\) і центр\((0,0)\)
    2. радіус є\(\sqrt{7}\) і центр\((0,0)\)
    3. радіус є\(9\) і центр\((-3,5)\)
    4. радіус є\(7\) і центр\((-2,-5)\)
    5. центр є\((3,6)\) і точка на колі\((3,-2)\)
    6. центр є\((2,2)\) і точка на колі\((4,4)\)
    Відповідь

    2. \(x^{2}+y^{2}=7\)

    4. \((x+2)^{2}+(y+5)^{2}=49\)

    6. \((x-2)^{2}+(y-2)^{2}=8\)

    Вправа\(\PageIndex{4}\) Graph a Circle

    У наступних вправах

    1. Знайдіть центр і радіус, потім
    2. Графік кожного кола.
    1. \(2 x^{2}+2 y^{2}=450\)
    2. \(3 x^{2}+3 y^{2}=432\)
    3. \((x+3)^{2}+(y-5)^{2}=81\)
    4. \((x+2)^{2}+(y+5)^{2}=49\)
    5. \(x^{2}+y^{2}-6 x-12 y-19=0\)
    6. \(x^{2}+y^{2}-4 y-60=0\)
    Відповідь

    2.

    1. радіус:\(12,\) центр:\((0,0)\)
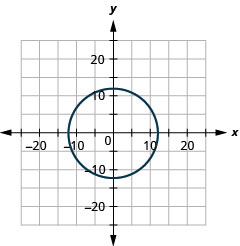
    На малюнку показано коло з графіком на координатній площині x y. Вісь X площини проходить від негативних 20 до 20. Вісь Y площини проходить від негативних 15 до 15. Центр кола дорівнює (0, 0), а радіус кола - 12.
    Малюнок 11.E.1

    4.

    1. радіус:\(7,\) центр:\((-2,-5)\)
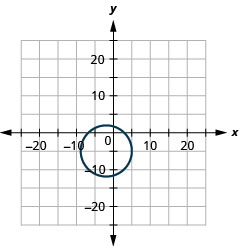
    На малюнку показано коло з графіком на координатній площині x y. Вісь X площини проходить від негативних 20 до 20. Вісь Y площини проходить від негативних 15 до 15. Центр кола дорівнює (негативний 2, негативний 5), а радіус кола - 7.
    Малюнок 11.E.2

    6.

    1. радіус:\(8,\) центр:\((0,2)\)
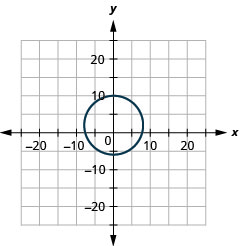
    На малюнку показано коло з графіком на координатній площині x y. Вісь X площини проходить від негативних 20 до 20. Вісь Y площини проходить від негативних 15 до 15. Центр кола дорівнює (0, 2), а радіус кола - 8.
    Малюнок 11.E.3

    Параболи

    Вправа\(\PageIndex{5}\) Graph Vertical Parabolas

    У наступних вправах складіть графік кожного рівняння, використовуючи його властивості.

    1. \(y=x^{2}+4 x-3\)
    2. \(y=2 x^{2}+10 x+7\)
    3. \(y=-6 x^{2}+12 x-1\)
    4. \(y=-x^{2}+10 x\)
    Відповідь

    2.

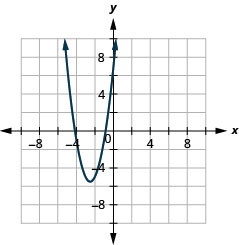
    На малюнку показана парабола, що відкривається вгору, графічна на координатній площині x y. Вісь X площини проходить від негативних 10 до 10. Вісь Y площини проходить від негативних 7 до 7. Вершина є (негативні п'ятиполовинки, негативні одинадцятиполовинки), а парабола проходить через точки (негативна 4, негативна 1) і (негативна 1, негативна 1).
    Малюнок 11.E.4

    4.

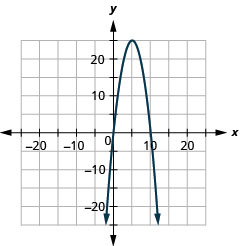
    На малюнку показана парабола, що відкривається вниз, графічна на координатній площині x y. Вісь X площини проходить від негативних 36 до 36. Вісь Y площини проходить від негативних 26 до 26. Вершина є (5, 25), а парабола проходить через точки (2, 16) і (8, 16).
    Малюнок 11.E.5
    Вправа\(\PageIndex{6}\) Graph Vertical Parabolas

    У наступних вправах

    1. Запишіть рівняння в стандартному вигляді, потім
    2. Використовуйте властивості стандартної форми для побудови графіка рівняння.
    1. \(y=x^{2}+4 x+7\)
    2. \(y=2 x^{2}-4 x-2\)
    3. \(y=-3 x^{2}-18 x-29\)
    4. \(y=-x^{2}+12 x-35\)
    Відповідь

    2.

    1. \(y=2(x-1)^{2}-4\)
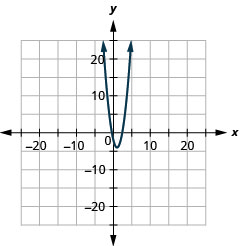
    На малюнку показана парабола, що відкривається вгору, графічна на координатній площині x y. Вісь X площини проходить від негативних 22 до 22. Вісь Y площини проходить від негативних 16 до 16. Вершина є (1, негативна 4), а парабола проходить через точки (0, негативні 2) і (2, негативні 2).
    Малюнок 11.E.6

    4.

    1. \(y=-(x-6)^{2}+1\)
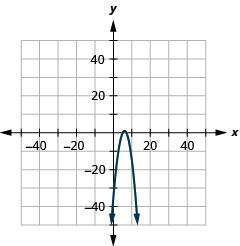
    На малюнку показана парабола, що відкривається вниз, графічна на координатній площині x y. Вісь X площини проходить від негативних 60 до 60. Вісь Y площини проходить від негативних 46 до 46. Вершина є (6, 1), а парабола проходить через точки (5, 0) і (7, 0).
    Малюнок 11.E.7
    Вправа\(\PageIndex{7}\) Graph Horizontal Parabolas

    У наступних вправах складіть графік кожного рівняння, використовуючи його властивості.

    1. \(x=2 y^{2}\)
    2. \(x=2 y^{2}+4 y+6\)
    3. \(x=-y^{2}+2 y-4\)
    4. \(x=-3 y^{2}\)
    Відповідь

    2.

    На малюнку показана парабола, що відкривається праворуч, графічна на координатній площині x y. Вісь X площини проходить від негативних 10 до 10. Вісь Y площини проходить від негативних 8 до 8. Вершина є (4, негативна 1), а парабола проходить через точки (6, 0) і (6, негативний 2).
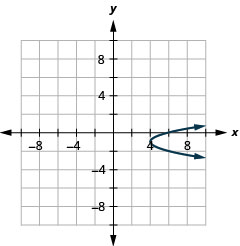
    Малюнок 11.E.8

    4.

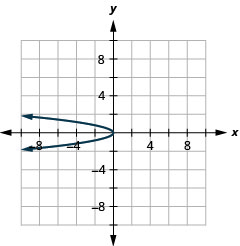
    На малюнку показана парабола, що відкривається вліво, графічна на координатній площині x y. Вісь X площини проходить від негативних 10 до 10. Вісь Y площини проходить від негативних 8 до 8. Вершина дорівнює (0, 0), а парабола проходить через точки (негативні 3, 1) і (негативні 3, негативні 1).
    Малюнок 11.E.9
    Вправа\(\PageIndex{8}\) Graph Horizontal Parabolas

    У наступних вправах

    1. Запишіть рівняння в стандартному вигляді, потім
    2. Використовуйте властивості стандартної форми для побудови графіка рівняння.
    1. \(x=4 y^{2}+8 y\)
    2. \(x=y^{2}+4 y+5\)
    3. \(x=-y^{2}-6 y-7\)
    4. \(x=-2 y^{2}+4 y\)
    Відповідь

    2.

    1. \(x=(y+2)^{2}+1\)
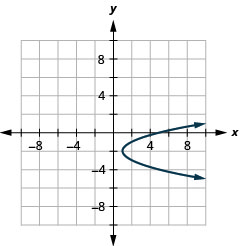
    На малюнку показана парабола, що відкривається праворуч, графічна на координатній площині x y. Вісь X площини проходить від негативних 10 до 10. Вісь Y площини проходить від негативних 8 до 8. Вершина є (1, негативна 2), а парабола проходить через точки (5, 0) і (5, негативні 4).
    Малюнок 11.E.10

    4.

    1. \(x=-2(y-1)^{2}+2\)
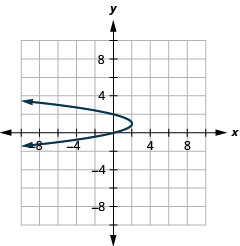
    На малюнку показана парабола, що відкривається вліво, графічна на координатній площині x y. Вісь X площини проходить від негативних 10 до 10. Вісь Y площини проходить від негативних 8 до 8. Вершина є (2, негативна 3), а парабола проходить через точки (0, 2) і (0, 0).
    Малюнок 11.E.11
    Вправа\(\PageIndex{9}\) Solve Applications with Parabolas

    У наступних вправах створіть рівняння параболічної арки, утвореної в фундаменті показаного моста. Дайте відповідь в стандартній формі.

    1.

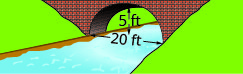
    На малюнку зображена параболічна арка, утворена в фундаменті моста. Арка висотою 5 футів і шириною 20 футів.
    Малюнок 11.E.12

    2.

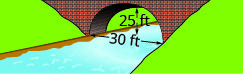
    На малюнку зображена параболічна арка, утворена в фундаменті моста. Арка висотою 25 футів і шириною 30 футів.
    Малюнок 11.E.13
    Відповідь

    2. \(y=-\frac{1}{9} x^{2}+\frac{10}{3} x\)

    еліпси

    Вправа\(\PageIndex{10}\) Graph an Ellipse with Center at the Origin

    У наступних вправах намалюйте графік кожного еліпса.

    1. \(\frac{x^{2}}{36}+\frac{y^{2}}{25}=1\)
    2. \(\frac{x^{2}}{4}+\frac{y^{2}}{81}=1\)
    3. \(49 x^{2}+64 y^{2}=3136\)
    4. \(9 x^{2}+y^{2}=9\)
    Відповідь

    2.

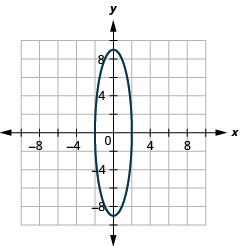
    На малюнку показано еліпс, зображений на координатній площині x y. Вісь X площини проходить від негативних 14 до 14. Вісь Y площини проходить від негативних 10 до 10. Еліпс має центр (0, 0), вертикальну велику вісь, вершини в (0, плюс або мінус 9) і співвершини в (плюс або мінус 2, 0).
    Малюнок 11.E.14

    4.

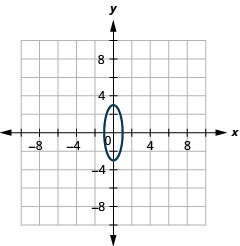
    На малюнку показано еліпс, зображений на координатній площині x y. Вісь Х площини проходить від негативних 9 до 9. Вісь Y площини проходить від негативних 7 до 7. Еліпс має центр (0, 0), вертикальну велику вісь, вершини в (0, плюс або мінус 3) і співвершини в (плюс або мінус 1, 0).
    Малюнок 11.E.15
    Вправа\(\PageIndex{11}\) Find the Equation of an Ellipse with Center at the Origin

    У наступних вправах знайдіть рівняння еліпса, показане на графіку.

    1.

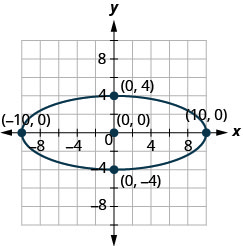
    На малюнку показано еліпс, зображений на координатній площині x y. Еліпс має центр (0, 0), горизонтальну велику вісь, вершини в (плюс або мінус 10, 0) і співвершини в (0, плюс або мінус 4).
    Малюнок 11.E.16

    2.

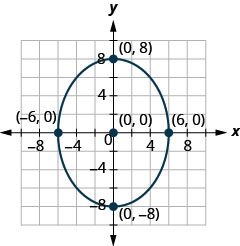
    На малюнку показано еліпс, зображений на координатній площині x y. Еліпс має центр (0, 0), вертикальну велику вісь, вершини в (0, плюс або мінус 8) і співвершини в (плюс або мінус 6, 0).
    Малюнок 11.E.17
    Відповідь

    2. \(\frac{x^{2}}{36}+\frac{y^{2}}{64}=1\)

    Вправа\(\PageIndex{12}\) Graph an Ellipse with Center Not at the Origin

    У наступних вправах намалюйте графік кожного еліпса.

    1. \(\frac{(x-1)^{2}}{25}+\frac{(y-6)^{2}}{4}=1\)
    2. \(\frac{(x+4)^{2}}{16}+\frac{(y+1)^{2}}{9}=1\)
    3. \(\frac{(x-5)^{2}}{16}+\frac{(y+3)^{2}}{36}=1\)
    4. \(\frac{(x+3)^{2}}{9}+\frac{(y-2)^{2}}{25}=1\)
    Відповідь

    2.

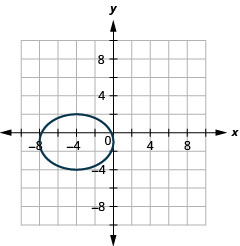
    На малюнку показано еліпс, зображений на координатній площині x y. Вісь X площини проходить від негативних 14 до 14. Вісь Y площини проходить від негативних 10 до 10. Еліпс має центр в (від'ємний 4, негативний 1), горизонтальну велику вісь, вершини в (від'ємний 8, негативний 1) і (0, негативний 1) і спів-вершини в (від'ємний 4, 2) і (негативний 4, негативний 4).
    Малюнок 11.E.18

    4.

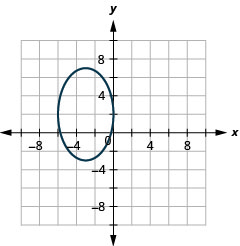
    На малюнку показано еліпс, зображений на координатній площині x y. Вісь X площини проходить від негативних 14 до 14. Вісь Y площини проходить від негативних 10 до 10. Еліпс має центр в (від'ємний 3, 2), вертикальну велику вісь, вершини в (від'ємний 3, 7) і (негативний 3, від'ємний 3) і спів-вершини в (від'ємні 6, 2) і (0, 2).
    Малюнок 11.E.19
    Вправа\(\PageIndex{13}\) Graph an Ellipse with Center Not at the Origin

    У наступних вправах

    1. Запишіть рівняння в стандартному вигляді і
    2. Графік.
    1. \(x^{2}+y^{2}+12 x+40 y+120=0\)
    2. \(25 x^{2}+4 y^{2}-150 x-56 y+321=0\)
    3. \(25 x^{2}+4 y^{2}+150 x+125=0\)
    4. \(4 x^{2}+9 y^{2}-126 x+405=0\)
    Відповідь

    2.

    1. \(\frac{(x-3)^{2}}{4}+\frac{(y-7)^{2}}{25}=1\)
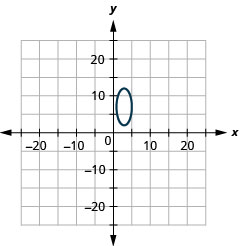
    На малюнку показано еліпс, зображений на координатній площині x y. Вісь Х площини проходить від негативних 18 до 18. Вісь Y площини проходить від негативних 14 до 14. Еліпс має центр в (3, 7), вертикальну велику вісь, вершини в (3, 2) і (3, 12) і співвершини в (від'ємні 1, 7) і (5, 7).
    Малюнок 11.E.20

    4.

    1. \(\frac{x^{2}}{9}+\frac{(y-7)^{2}}{4}=1\)
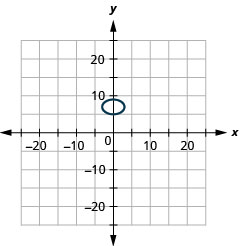
    На малюнку показано еліпс, зображений на координатній площині x y. Вісь Х площини проходить від негативних 15 до 15. Вісь Y площини проходить від негативних 11 до 11. Еліпс має центр в (0, 7), горизонтальну велику вісь, вершини в (3, 7) і (від'ємні 3, 7) і співвершини в (0, 5) і (0, 9).
    Малюнок 11.E.21
    Вправа\(\PageIndex{14}\) Solve Applications with Ellipses

    У наступних вправах напишіть рівняння описуваного еліпса.

    1. Комета рухається по еліптичній орбіті навколо Сонця. Найближча комета потрапляє до сонця приблизно\(10\) AU, а найдальша - приблизно\(90\) AU. Сонце є одним з вогнищ еліптичної орбіти. Допустивши центр еліпса у початку та маркування осей в АС, орбіта буде виглядати як на малюнку нижче. Використовуйте графік, щоб написати рівняння для еліптичної орбіти комети.
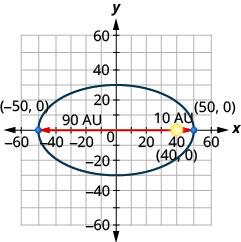
    На малюнку показана модель еліптичної орбіти навколо Сонця на координатній площині x y. Еліпс має центр в (0, 0), горизонтальну велику вісь, вершини, позначені в (плюс або мінус 50, 0), сонце, позначене як вогнище і позначене (50, 0), найближча відстань комета знаходиться від сонця, позначеного як 10 A U, а найдальша комета - від сонця, позначеного як 90 A U.
    Малюнок 11.E.22
    Відповідь

    1. Вирішити

    Гіперболи

    Вправа\(\PageIndex{15}\) Graph a Hyperbola with Center at \((0,0)\)

    У наступних вправах граф.

    1. \(\frac{x^{2}}{25}-\frac{y^{2}}{9}=1\)
    2. \(\frac{y^{2}}{49}-\frac{x^{2}}{16}=1\)
    3. \(9 y^{2}-16 x^{2}=144\)
    4. \(16 x^{2}-4 y^{2}=64\)
    Відповідь

    1.

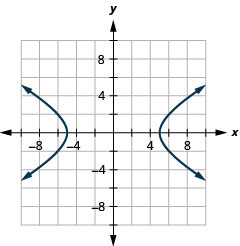
    На малюнку зображена гіпербола, зображена на координатній площині x y. Вісь Х площини проходить від негативних 12 до 12. Вісь Y площини проходить від негативних 9 до 9. Гіпербола має центр в (0, 0) і гілки, які проходять через вершини (плюс або мінус 5, 0), і які відкриваються вліво і вправо.
    Малюнок 11.E.23

    3.

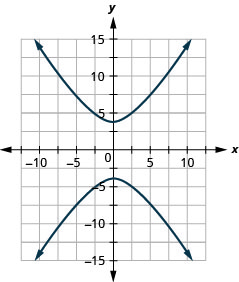
    На малюнку зображена гіпербола, зображена на координатній площині x y. Вісь Х площини проходить від негативного 19 до 19. Вісь Y площини проходить від негативних 15 до 15. Гіпербола має центр в (0, 0) і гілки, які проходять через вершини (0, плюс або мінус 4), і які відкриваються вгору і вниз.
    Малюнок 11.E.24
    Вправа\(\PageIndex{16}\) Graph a Hyperbola with Center at \((h,k)\)

    У наступних вправах граф.

    1. \(\frac{(x+1)^{2}}{4}-\frac{(y+1)^{2}}{9}=1\)
    2. \(\frac{(x-2)^{2}}{4}-\frac{(y-3)^{2}}{16}=1\)
    3. \(\frac{(y+2)^{2}}{9}-\frac{(x+1)^{2}}{9}=1\)
    4. \(\frac{(y-1)^{2}}{25}-\frac{(x-2)^{2}}{9}=1\)
    Відповідь

    1.

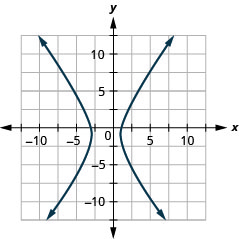
    На малюнку зображена гіпербола, зображена на координатній площині x y. Вісь X площини проходить від негативних 14 до 14. Вісь Y площини проходить від негативних 10 до 10. Гіпербола має центр в (негативний 1, негативний 1) і гілки, які проходять через вершини (негативні 3, негативні 1) і (1, негативні 1), і які відкриваються вліво і вправо.
    Малюнок 11.E.25

    3.

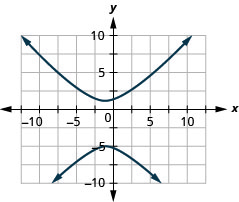
    На малюнку зображена гіпербола, зображена на координатній площині x y. Вісь X площини проходить від негативних 14 до 14. Вісь Y площини проходить від негативних 10 до 10. Гіпербола має центр в (негативний 1, негативний 2) і гілки, які проходять через вершини (негативні 1, 1) і (негативні 1, негативні 5), і які відкриваються вгору і вниз.
    Малюнок 11.E.26
    Вправа\(\PageIndex{17}\) Graph a Hyperbola with Center at \((h,k)\)

    У наступних вправах

    1. Запишіть рівняння в стандартному вигляді і
    2. Графік.
    1. \(4 x^{2}-16 y^{2}+8 x+96 y-204=0\)
    2. \(16 x^{2}-4 y^{2}-64 x-24 y-36=0\)
    3. \(4 y^{2}-16 x^{2}+32 x-8 y-76=0\)
    4. \(36 y^{2}-16 x^{2}-96 x+216 y-396=0\)
    Відповідь

    1.

    1. \(\frac{(x+1)^{2}}{16}-\frac{(y-3)^{2}}{4}=1\)
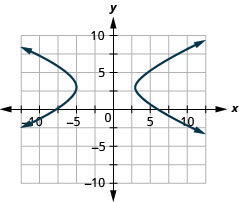
    На малюнку зображена гіпербола, зображена на координатній площині x y. Вісь X площини проходить від негативних 14 до 14. Вісь Y площини проходить від негативних 10 до 10. Гіпербола має центр в (негативний 1, 3) і гілки, які проходять через вершини (негативні 5, 3) і (3, 3), і які відкриваються вліво і вправо.
    Малюнок 11.E.27

    3.

    1. \(\frac{(y-1)^{2}}{16}-\frac{(x-1)^{2}}{4}=1\)
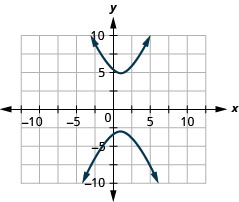
    На малюнку зображена гіпербола, зображена на координатній площині x y. Вісь X площини проходить від негативних 14 до 14. Вісь Y площини проходить від негативних 10 до 10. Гіпербола має центр в (1, 1) і гілки, які проходять через вершини (1, негативні 3) і (1, 5), і які відкриваються вгору і вниз.
    Малюнок 11.E.28
    Вправа\(\PageIndex{18}\) Identify the Graph of Each Equation as a Circle, Parabola, Ellipse, or Hyperbola

    У наступних вправах визначте тип графіка.

      1. \(16 y^{2}-9 x^{2}-36 x-96 y-36=0\)
      2. \(x^{2}+y^{2}-4 x+10 y-7=0\)
      3. \(y=x^{2}-2 x+3\)
      4. \(25 x^{2}+9 y^{2}=225\)
      1. \(x^{2}+y^{2}+4 x-10 y+25=0\)
      2. \(y^{2}-x^{2}-4 y+2 x-6=0\)
      3. \(x=-y^{2}-2 y+3\)
      4. \(16 x^{2}+9 y^{2}=144\)
    Відповідь

    1.

    1. Гіпербола
    2. Коло
    3. Парабола
    4. Еліпс

    Розв'язуйте системи нелінійних рівнянь

    Вправа\(\PageIndex{19}\) Solve a System of Nonlinear Equations Using Graphing

    У наступних вправах розв'яжіть систему рівнянь за допомогою графіки.

    1. \(\left\{\begin{array}{l}{3 x^{2}-y=0} \\ {y=2 x-1}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{y=x^{2}-4} \\ {y=x-4}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{x^{2}+y^{2}=169} \\ {x=12}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {y=-5}\end{array}\right.\)
    Відповідь

    1.

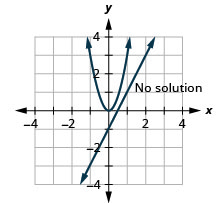
    На малюнку показана парабола та лінія, розміщена на координатній площині x y. Вісь X площини проходить від негативних 5 до 5. Вісь Y площини проходить від негативних 4 до 4. Парабола має вершину в (0, 0) і відкривається вгору. Лінія має нахил 2 з y-перехопленням при негативному 1. Парабола і лінія не перетинаються, тому система не має рішення.
    Малюнок 11.E.29

    3.

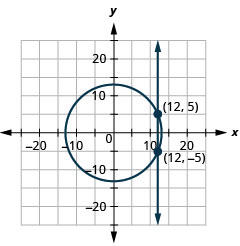
    На малюнку показано коло та лінію, розміщені на координатній площині x y. Вісь X площини проходить від негативних 20 до 20. Вісь Y площини проходить від негативних 15 до 15. Коло має центр в (0, 0) і радіус 13. Лінія вертикальна. Коло і лінія перетинаються в точках (12, 5) і (12, негативні 5), які позначені. Рішення системи є (12, 5) і (12, негативний 5)
    Малюнок 11.E.30
    Вправа\(\PageIndex{20}\) Solve a System of Nonlinear Equations Using Substitution

    У наступних вправах вирішуйте систему рівнянь за допомогою підстановки.

    1. \(\left\{\begin{array}{l}{y=x^{2}+3} \\ {y=-2 x+2}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x-y=4}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{9 x^{2}+4 y^{2}=36} \\ {y-x=5}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{x^{2}+4 y^{2}=4} \\ {2 x-y=1}\end{array}\right.\)
    Відповідь

    1. \((-1,4)\)

    3. Немає рішення

    Вправа\(\PageIndex{21}\) Solve a System of Nonlinear Equations Using Elimination

    У наступних вправах вирішуйте систему рівнянь за допомогою елімінації.

    1. \(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-2 y-1=0}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{x^{2}-y^{2}=5} \\ {-2 x^{2}-3 y^{2}=-30}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{4 x^{2}+9 y^{2}=36} \\ {3 y^{2}-4 x=12}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{x^{2}+y^{2}=14} \\ {x^{2}-y^{2}=16}\end{array}\right.\)
    Відповідь

    1. \((-\sqrt{7}, 3),(\sqrt{7}, 3)\)

    3. \((-3,0),(0,-2),(0,2)\)

    Вправа\(\PageIndex{22}\) Use a System of Nonlinear Equations to Solve Applications

    У наступних вправах вирішуйте задачу за допомогою системи рівнянь.

    1. Сума квадратів двох чисел дорівнює\(25\). Різниця чисел є\(1\). Знайдіть цифри.
    2. Різниця квадратів двох чисел дорівнює\(45\). Різниця квадрата першого числа і подвійного квадрата другого числа дорівнює\(9\). Знайдіть цифри.
    3. Периметр прямокутника -\(58\) метри, а його площа -\(210\) квадратні метри. Знайдіть довжину і ширину прямокутника.
    4. Колтон придбав для своєї кухні мікрохвильовку більшого розміру. Діагональ передньої частини мікрохвильовки вимірює\(34\) дюйми. Передня частина також має площу\(480\) квадратних дюймів. Яка довжина і ширина мікрохвильовки?
    Відповідь

    1. \(-3\)і\(-4\) або\(4\) і\(3\)

    3. Якщо довжина дорівнює\(14\) дюймам, ширина дорівнює\(15\) дюймам. Якщо довжина дорівнює\(15\) дюймам, ширина дорівнює\(14\) дюймам.

    Практичний тест

    Вправа\(\PageIndex{23}\)

    У наступних вправах знайдіть відстань між точками і серединою відрізка лінії з заданими кінцевими точками. Округляйте до найближчої десятої в міру необхідності.

    1. \((-4,-3)\)і\((-10,-11)\)
    2. \((6,8)\)і\((-5,-3)\)
    Відповідь

    1. відстань:\(10,\) середина:\((-7,-7)\)

    Вправа\(\PageIndex{24}\)

    У наступних вправах запишіть стандартну форму рівняння кола з заданою інформацією.

    1. радіус є\(11\) і центр\((0,0)\)
    2. радіус є\(12\) і центр\((10,-2)\)
    3. центр є\((-2,3)\) і точка на колі\((2,-3)\)
    4. Знайдіть рівняння еліпса, показане на графіку.
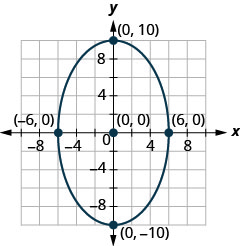
    На малюнку показано еліпс, зображений на координатній площині x y. Еліпс має центр (0, 0), вертикальну велику вісь, вершини в (0, плюс або мінус 10) і співвершини в (плюс або мінус 6, 0).
    Малюнок 11.E.31
    Відповідь

    1. \(x^{2}+y^{2}=121\)

    3. \((x+2)^{2}+(y-3)^{2}=52\)

    Вправа\(\PageIndex{25}\)

    У наступних вправах

    1. Визначте тип графіка кожного рівняння як коло, парабола, еліпс або гіпербола, і
    2. Графік рівняння.
    1. \(4 x^{2}+49 y^{2}=196\)
    2. \(y=3(x-2)^{2}-2\)
    3. \(3 x^{2}+3 y^{2}=27\)
    4. \(\frac{y^{2}}{100}-\frac{x^{2}}{36}=1\)
    5. \(\frac{x^{2}}{16}+\frac{y^{2}}{81}=1\)
    6. \(x=2 y^{2}+10 y+7\)
    7. \(64 x^{2}-9 y^{2}=576\)
    Відповідь

    1.

    1. Еліпс
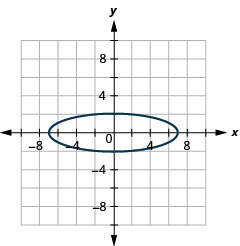
    На малюнку показано еліпс, зображений на координатній площині x y. Вісь X площини проходить від негативних 10 до 10. Вісь Y площини проходить від негативних 8 до 8. Еліпс має центр в (0, 0), горизонтальну велику вісь, вершини в (плюс або мінус 7, 0) і спів-вершини в (0, плюс або мінус 2).
    Малюнок 11.E.32

    3.

    1. Коло
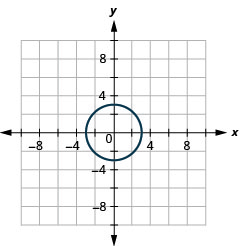
    На малюнку показано коло з графіком на координатній площині x y. Вісь X площини проходить від негативних 10 до 10. Вісь Y площини проходить від негативних 8 до 8. Коло параболи має центр в (0, 0) і радіус 3.
    Малюнок 11.E.33

    5.

    1. Еліпс
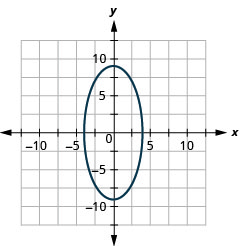
    На малюнку показано еліпс, зображений на координатній площині x y. Вісь X площини проходить від негативних 14 до 14. Вісь Y площини проходить від негативних 10 до 10. Еліпс має центр в (0, 0), вертикальну велику вісь, вершини в (0, плюс або мінус 9) і спів-вершини в (плюс або мінус 4, 0).
    Малюнок 11.E.34

    7.

    1. Гіпербола
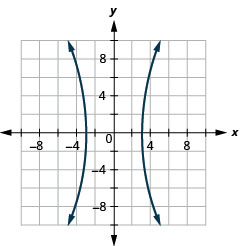
    На малюнку зображена гіпербола, зображена на координатній площині x y. Вісь X площини проходить від негативних 10 до 10. Вісь Y площини проходить від негативних 8 до 8. Гіпербола має центр в (0, 0) і гілки, які проходять через вершини (плюс або мінус 3, 0) і які відкриваються вліво і вправо.
    Малюнок 11.E.35
    Вправа\(\PageIndex{26}\)

    У наступних вправах

    1. Визначте тип графіка кожного рівняння як коло, парабола, еліпс або гіпербола,
    2. Запишіть рівняння в стандартному вигляді, і
    3. Графік рівняння.
    1. \(25 x^{2}+64 y^{2}+200 x-256 y-944=0\)
    2. \(x^{2}+y^{2}+10 x+6 y+30=0\)
    3. \(x=-y^{2}+2 y-4\)
    4. \(9 x^{2}-25 y^{2}-36 x-50 y-214=0\)
    5. \(y=x^{2}+6 x+8\)
    6. Розв'яжіть нелінійну систему рівнянь шляхом побудови графіків:\(\left\{\begin{array}{l}{3 y^{2}-x=0} \\ {y=-2 x-1}\end{array}\right.\).
    7. Розв'яжіть нелінійну систему рівнянь за допомогою підстановки:\(\left\{\begin{array}{l}{x^{2}+y^{2}=8} \\ {y=-x-4}\end{array}\right.\).
    8. Вирішити нелінійну систему рівнянь за допомогою елімінації:\(\left\{\begin{array}{l}{x^{2}+9 y^{2}=9} \\ {2 x^{2}-9 y^{2}=18}\end{array}\right.\)
    9. Створіть рівняння параболічної арки, утвореної в фундаменті показаного моста. Дайте відповідь у\(y=a x^{2}+b x+c\) формі.
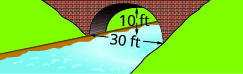
    На малюнку зображена параболічна арка, утворена в фундаменті моста. Арка висотою 10 футів і шириною 30 футів.
    Малюнок 11.E.36

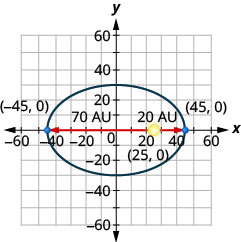
    10. Комета рухається по еліптичній орбіті навколо Сонця. Найближча комета потрапляє до сонця приблизно\(20\) AU, а найдальша - приблизно\(70\) AU. Сонце є одним з вогнищ еліптичної орбіти. Допустивши центр еліпса у початку та маркування осей в АС, орбіта буде виглядати як на малюнку нижче. Використовуйте графік, щоб написати рівняння для еліптичної орбіти комети.

    На малюнку показана модель еліптичної орбіти навколо Сонця на координатній площині x y. Еліпс має центр в (0, 0), горизонтальну велику вісь, вершини, позначені в (плюс або мінус 45, 0), сонце, позначене як вогнище і позначене (25, 0), найближча відстань комета знаходиться від сонця, позначеного як 20 A U, а найдальша комета - від сонця, позначеного як 70 A U.
    Малюнок 11.E.37

    11. Сума двох чисел є,\(22\) а добуток дорівнює\(−240\). Знайдіть цифри.

    12. На день народження бабусі і дідусі Олива купили їй новий широкоекранний телевізор. Перед відкриттям вона хоче переконатися, що вона буде відповідати її розважальний центр. Телевізор є\(55\)». Розмір телевізора вимірюється по діагоналі екрану, а широкоформатний має довжину, яка більше ширини. Екран також має площу\(1452\) квадратних дюймів. Її розважальний центр має вставку для телевізора довжиною в\(50\) дюйми і шириною в\(40\) дюйми. Яка довжина і ширина екрану телевізора і чи підійде він розважальному центру Olive?

    Відповідь

    2.

    1. Коло
    2. \((x+5)^{2}+(y+3)^{2}=4\)
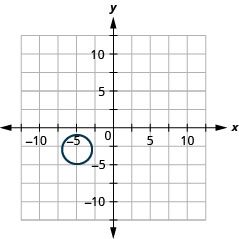
    На малюнку показано коло з графіком на координатній площині x y. Вісь X площини проходить від негативних 14 до 14. Вісь Y площини проходить від негативних 10 до 10. Коло має центр в (від'ємний 5, негативний 3) і радіус 2.
    Малюнок 11.E.38

    4.

    1. Гіпербола
    2. \(\frac{(x-2)^{2}}{25}-\frac{(y+1)^{2}}{9}=1\)
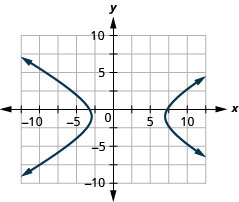
    На малюнку зображена гіпербола, зображена на координатній площині x y. Вісь X площини проходить від негативних 14 до 14. Вісь Y площини проходить від негативних 10 до 10. Гіпербола має центр в (2, негативний 1) і гілки, які проходять через вершини (негативні 3, негативні 1) і (7, негативні 1), які відкриваються вліво і вправо.
    Малюнок 11.E.39

    6. Немає рішення

    8. \((0,-3),(0,3)\)

    10. \(\frac{x^{2}}{2025}+\frac{y^{2}}{1400}=1\)

    12. Довжина -\(44\) дюйми, а ширина -\(33\) дюйми. Телевізор підійде до розважального центру Olive.

    Глосарій

    система нелінійних рівнянь
    Система нелінійних рівнянь - це система, де принаймні одне з рівнянь не є лінійним.