11.5: Гіперболи
- Page ID
- 59814
До кінця цього розділу ви зможете:
- Графік гіперболи з центром в\((0,0)\)
- Графік гіперболи з центром в\((h,k)\)
- Визначити конічні перерізи за їх рівняннями
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Вирішити:\(x^{2}=12\).
Якщо ви пропустили цю проблему, перегляньте приклад 9.1. - Розгорнути:\((x−4)^{2}\).
Якщо ви пропустили цю проблему, перегляньте приклад 5.32. - Графік\(y=-\frac{2}{3} x\).
Якщо ви пропустили цю проблему, перегляньте приклад 3.4.
Графік Гіпербола з центром в\((0,0)\)
Останній конічний розріз, який ми розглянемо, називається гіперболою. Ми побачимо, що рівняння гіперболи виглядає так само, як рівняння еліпса, за винятком того, що це різниця, а не сума. Хоча рівняння еліпса і гіперболи дуже схожі, їх графіки дуже різні.
Ми визначаємо гіперболу як усі точки на площині, де різниця їх відстаней від двох фіксованих точок є постійною. Кожна з нерухомих точок називається вогнищем гіперболи.
Гіпербола - це всі точки на площині, де різниця їх відстаней від двох нерухомих точок постійна. Кожна з нерухомих точок називається вогнищем гіперболи.
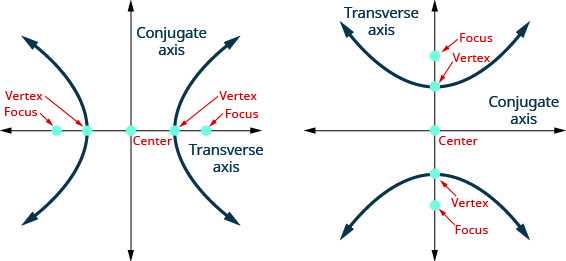
Лінія, що проходить через вогнища, називається поперечною віссю. Дві точки, де поперечна вісь перетинає гіперболу, є кожною вершиною гіперболи. Середина сегмента, що приєднується до вогнищ, називається центром гіперболи. Лінія, перпендикулярна поперечній осі, яка проходить через центр, називається сполученою віссю. Кожен шматок графіка називається гілкою гіперболи.
Знову наша мета полягає в тому, щоб з'єднати геометрію конічного конуса з алгеброю. Розміщення гіперболи на прямокутній системі координат дає нам таку можливість. На малюнку ми розмістили гіперболу так, щоб вогнища\(((−c,0),(c,0))\) знаходилися на\(x\) -осі, а центр - початок.
Визначення стверджує, що різниця відстані від вогнищ до точки\((x,y)\) постійна. Так\(|d_{1}−d_{2}|\) це константа, яку ми\(2a\) так назвемо\(|d_{1}-d_{2} |=2 a\). Ми будемо використовувати формулу відстані, щоб привести нас до алгебраїчної формули для еліпса.
\(\left|d_{1} - d_{2}\right| =2 a\)
Використовуйте формулу відстані, щоб знайти\(d_{1}, d_{2}\)
\(\left|\sqrt{(x-(-c))^{2}+(y-0)^{2}}-\sqrt{(x-c)^{2}+(y-0)^{2}}\right|=2 a\)
Усуньте радикали. Щоб спростити рівняння еліпса, давайте\(c^{2}-a^{2}=b^{2}\).
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{c^{2}-a^{2}}=1\)
Отже, рівняння гіперболи, зосередженої на початку в стандартному вигляді, таке:
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)
Щоб зробити графік гіперболи, корисно буде знати про перехоплення. Ми знайдемо\(x\) -перехоплення і\(y\) -перехоплення за формулою.
\(x\)-перехоплює
Нехай\(y=0\).
\(\begin{aligned} \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}}-\frac{0^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}} &=1 \\ x^{2} &=a^{2} \\ x &=\pm a \end{aligned}\)
\(x\)-перехоплює є\((a,0)\) і\((−a,0)\).
\(y\)-перехоплює
Нехай\(x=0\).
\(\begin{aligned} \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} &=1 \\ \frac{0^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} &=1 \\-\frac{y^{2}}{b^{2}} &=1 \\ y^{2} &=-b^{2} \\ y &=\pm \sqrt{-b^{2}} \end{aligned}\)
Немає\(y\) -перехоплень.
\(a, b\)Значення в рівнянні також допомагають нам знайти асимптоти гіперболи. Асимптоти - це перетинаються прямі лінії, до яких наближаються гілки графа, але ніколи не перетинаються, оскільки\(x, y\) значення стають більшими та більшими.
Щоб знайти асимптоти, ми намалюємо прямокутник, сторони якого перетинають вісь x у вершині\((−a,0),(a,0)\), і перетинаємо\(y\) вісь -в\((0,−b), (0,b)\). Рядки, що містять діагоналі цього прямокутника, є асимптотами гіперболи. Прямокутник і асимптоти не є частиною гіперболи, але вони допомагають нам скласти графік гіперболи.
Асимптоти проходять через початок, і ми можемо оцінити їх нахил за допомогою прямокутника, який ми намалювали. Вони мають рівняння\(y=\frac{b}{a} x\) і\(y=-\frac{b}{a} x\).
Існує два рівняння для гіпербол, в залежності від того, вертикальна або горизонтальна поперечна вісь. Ми можемо визначити, чи горизонтальна поперечна вісь, дивлячись на рівняння. Коли рівняння знаходиться в стандартній формі, якщо\(x^{2}\) -член позитивний, поперечна вісь горизонтальна. Коли рівняння знаходиться в стандартній формі, якщо\(y^{2}\) -член позитивний, поперечна вісь вертикальна.
Другі рівняння можуть бути виведені аналогічно тому, що ми зробили. Підсумки ми підведемо тут.
Стандартна форма рівняння гіперболи з центром\((0,0)\)
Стандартна форма рівняння гіперболи з центром\((0,0)\), становить
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 \quad\)або\(\quad \frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\)
Зверніть увагу, що, на відміну від рівняння еліпса, знаменник не завжди\(a^{2}\) і знаменник не\(y^{2}\) завжди\(b^{2}\).\(x^{2}\)
Зверніть увагу, що коли\(x^{2}\) -термін позитивний, поперечна вісь знаходиться на\(x\) -осі. Коли\(y^{2}\) -термін позитивний, поперечна вісь знаходиться на\(y\) -осі.
Стандартні форми рівняння гіперболи з центром\((0,0)\)
| \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) | \(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\) | |
|---|---|---|
| Орієнтація | \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">Поперечна вісь на\(x\) -осі. Відкриває ліворуч і праворуч |
\ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">Поперечна вісь на\(y\) -осі. Відкриває вгору і вниз |
| Вершини | \ (\ розрив {x^ {2}} {a^ {2}} -\ розрив {y^ {2}} {b^ {2}} =1\) ">\((-a, 0),(a, 0)\) | \ (\ розрив {y^ {2}} {a^ {2}} -\ розрив {x^ {2}} {b^ {2}} =1\) ">\((0,-a),(0, a)\) |
| \(x\)-перехоплює | \ (\ розрив {x^ {2}} {a^ {2}} -\ розрив {y^ {2}} {b^ {2}} =1\) ">\((-a, 0),(a, 0)\) | \ (\ розрив {y^ {2}} {a^ {2}} -\ розрив {x^ {2}} {b^ {2}} =1\) ">немає |
| \(y\)-перехоплює | \ (\ розрив {x^ {2}} {a^ {2}} -\ розрив {y^ {2}} {b^ {2}} =1\) ">немає | \ (\ розрив {y^ {2}} {a^ {2}} -\ розрив {x^ {2}} {b^ {2}} =1\) ">\((0,-a),(0, a)\) |
| Прямокутник | \ (\ розрив {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">Використовувати\(( \pm a, 0)(0, \pm b)\) | \ (\ frac {y^ {2}} {a^ {2}} -\ розрив {x^ {2}} {b^ {2}} =1\) ">Використовувати\((0, \pm a)( \pm b, 0)\) |
| Асимптоти | \ (\ розрив {x^ {2}} {a^ {2}} -\ розрив {y^ {2}} {b^ {2}} =1\) ">\(y=\frac{b}{a} x, y=-\frac{b}{a} x\) | \ (\ розрив {y^ {2}} {a^ {2}} -\ розрив {x^ {2}} {b^ {2}} =1\) ">\(y=\frac{a}{b} x, y=-\frac{a}{b} x\) |
Ми будемо використовувати ці властивості для графування гіпербол.
Графік\(\frac{x^{2}}{25}-\frac{y^{2}}{4}=1\).
Рішення:
| Крок 1: Запишіть рівняння в стандартній формі. | Рівняння знаходиться в стандартній формі. | \(\frac{x^{2}}{25}-\frac{y^{2}}{4}=1\) |
| Крок 2: Визначте, горизонтальна чи вертикальна поперечна вісь. | Оскільки\(x^{2}\) -термін позитивний, поперечна вісь горизонтальна. | Поперечна вісь горизонтальна. |
| Крок 3: Знайдіть вершини. | З тих\(a^{2}=25\) пір\(a=\pm 5\). Вершини знаходяться на\(x\) -осі. | \((-5,0),(5,0)\) |
| Крок 4: Намалюйте прямокутник, зосереджений на початковому перетині однієї\(\pm a\) осі, а іншу на\(\pm b\). |
Так як\(a=\pm 5\), прямокутник буде перетинати\(x\) -вісь у вершині. Так як\(b=\pm 2\) прямокутник буде перетинатися з\(y\) -віссю в\((0,-2)\) і\((0,2)\). |
.png) |
|
Крок 5: Намалюйте асимптоти—лінії через діагоналі прямокутника. |
Асимптоти мають рівняння\(y=\frac{5}{2} x, y=-\frac{5}{2} x\). | .png) |
| Крок 6: Намалюйте дві гілки гіперболи. | Почніть з кожної вершини і використовуйте асимптоти як орієнтир. | 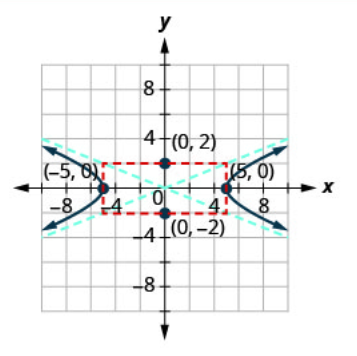.png) |
Графік\(\frac{x^{2}}{16}-\frac{y^{2}}{4}=1\).
- Відповідь
-
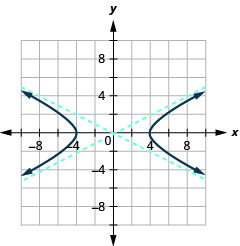
Малюнок 11.4.9
Графік\(\frac{x^{2}}{9}-\frac{y^{2}}{16}=1\).
- Відповідь
-
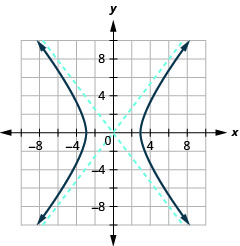
Малюнок 11.4.10
Підсумовуємо кроки для довідки.
Графік a Гіпербола з центром\((0,0)\)
- Запишіть рівняння в стандартному вигляді.
- Визначте, горизонтальна або вертикальна поперечна вісь.
- Знайдіть вершини.
- Намалюйте прямокутник, центрований у початковій точці, що перетинає одну вісь,\(±a\) а іншу в\(±b\).
- Намалюйте асимптоти—лінії через діагоналі прямокутника.
- Намалюйте дві гілки гіперболи.
Іноді рівняння для гіперболи потрібно спочатку помістити в стандартну форму, перш ніж ми його графуємо.
Графік\(4 y^{2}-16 x^{2}=64\).
Рішення:
| \(4 y^{2}-16 x^{2}=64\) | |
| Щоб записати рівняння в стандартній формі, розділіть кожен член на,\(64\) щоб рівняння було рівним\(1\). | \(\frac{4 y^{2}}{64}-\frac{16 x^{2}}{64}=\frac{64}{64}\) |
| Спростити. | \(\frac{y^{2}}{16}-\frac{x^{2}}{4}=1\) |
| Оскільки\(y^{2}\) -термін позитивний, поперечна вісь вертикальна. З тих\(a^{2}=16\) пір\(a=\pm 4\). | |
| Вершини знаходяться на\(y\) -осі,\((0,-a),(0, a)\). З тих\(b^{2}=4\) пір\(b=\pm 2\). | \((0,-4),(0,4)\) |
| Намалюйте прямокутник, що перетинає\(x\) -вісь at\((-2,0),(2,0)\) та\(y\) -вісь у вершині. Намалюйте асимптоти через діагоналі прямокутника. Намалюйте дві гілки гіперболи. | 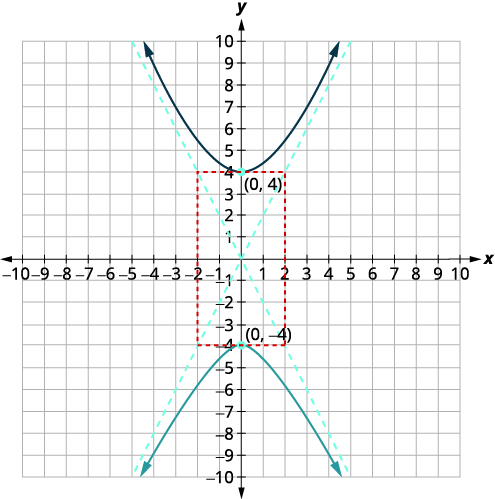 |
Графік\(4 y^{2}-25 x^{2}=100\).
- Відповідь
-
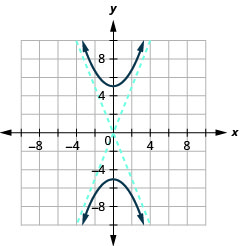
Малюнок 11.4.12
Графік\(25 y^{2}-9 x^{2}=225\).
- Відповідь
-
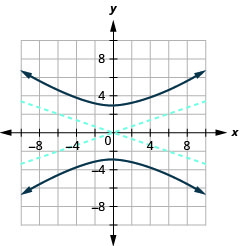
Малюнок 11.4.13
Графік Гіпербола з центром в\((h,k)\)
Гіперболи не завжди зосереджені на походженні. Коли гіпербола зосереджена на\((h,k)\) рівняннях трохи змінюється, як відображено в таблиці.
Стандартні форми рівняння гіперболи з центром\((h,k)\)
| \(\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1\) | \(\frac{(y-k)^{2}}{a^{2}}-\frac{(x-h)^{2}}{b^{2}}=1\) | |
|---|---|---|
| Орієнтація | \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">Поперечна вісь горизонтальна. Відкриває ліворуч і праворуч | \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">Поперечна вісь вертикальна. Відкриває вгору і вниз |
| Центр | \ (\ розрив {(x-h) ^ {2}} {a^ {2}} -\ розрив {(y-k) ^ {2}} {b^ {2}} =1\) ">\((h,k)\) | \ (\ розрив {(y-k) ^ {2}} {a^ {2}} -\ розрив {(x-h) ^ {2}} {b^ {2}} =1\) ">\((h,k)\) |
| Вершини | \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">\(a\) одиниці ліворуч і праворуч від центру | \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">\(a\) одиниці вище і нижче центру |
| Прямокутник | \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">Використовуйте\(a\) одиниці вліво/праворуч від центральних\(b\) одиниць над/нижче центру | \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">Використовуйте\(a\) одиниці над/нижче центральних\(b\) одиниць ліво/праворуч від центру |
Графік\(\frac{(x-1)^{2}}{9}-\frac{(y-2)^{2}}{16}=1\)
Рішення:
| Крок 1: Запишіть рівняння в стандартній формі. | Рівняння знаходиться в стандартній формі. | \(\frac{(x-1)^{2}}{9}-\frac{(y-2)^{2}}{16}=1\) |
| Крок 2: Визначте, горизонтальна чи вертикальна поперечна вісь. | Оскільки\(x^{2}\) -термін позитивний, гіпербола відкривається вліво і вправо. | Поперечна вісь горизонтальна. Гіпербола відкривається вліво і вправо. |
| Крок 3: Знайдіть центр і\(a, b\). | \(h=1\)і\(k=2\) \(a^{2}=9\) \(b^{2}=16\) |
\(\begin{array} {c} \frac{\left(\stackrel{\color{red}{x-h}}{\color{black}{x-1}} \right)^{2}}{9} - \frac{\left(\stackrel{\color{red}{y-k}}{\color{black}{y-2}} \right)^{2}}{16} = 1 \end{array}\) Центр:\((1,2)\) \(a=3\) \(b=4\) |
| Крок 4: Намалюйте прямокутник по центру при\((h,k)\) використанні\(a,b\). |
Відзначте центр,\((1,2)\). Намалюйте прямокутник, який проходить через точки\(3\) одиниць вліво/праворуч від центру та\(4\) одиниць вище та нижче центру. |
.png) |
| Крок 5: Намалюйте асимптоти—лінії через діагоналі прямокутника. Відзначте вершини. | Намалюйте діагоналі. Позначте вершини, які знаходяться на\(3\) одиницях прямокутника ліворуч і праворуч від центру. | .png) |
| Крок 6: Намалюйте дві гілки гіперболи. | Почніть з кожної вершини і використовуйте асимптоти як орієнтир. | .png) |
Графік\(\frac{(x-3)^{2}}{25}-\frac{(y-1)^{2}}{9}=1\).
- Відповідь
-
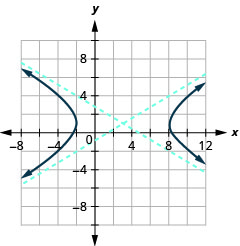
Малюнок 11.4.17
Графік\(\frac{(x-2)^{2}}{4}-\frac{(y-2)^{2}}{9}=1\).
- Відповідь
-
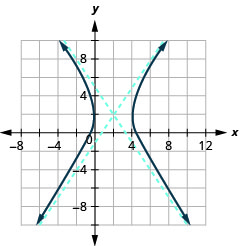
Малюнок 11.4.18
Ми підсумовуємо кроки для зручності ознайомлення.
Графік a Гіпербола з центром\((h,k)\)
- Запишіть рівняння в стандартному вигляді.
- Визначте, горизонтальна або вертикальна поперечна вісь.
- Знайдіть центр і\(a,b\).
- Намалюйте прямокутник по центру\((h,k)\) за допомогою\(a,b\).
- Намалюйте асимптоти—лінії через діагоналі прямокутника. Відзначте вершини.
- Намалюйте дві гілки гіперболи.
Будьте обережні, коли ви ідентифікуєте центр. Стандартне рівняння має\(x−h\) і\(y−k\) з центром як\((h,k)\).
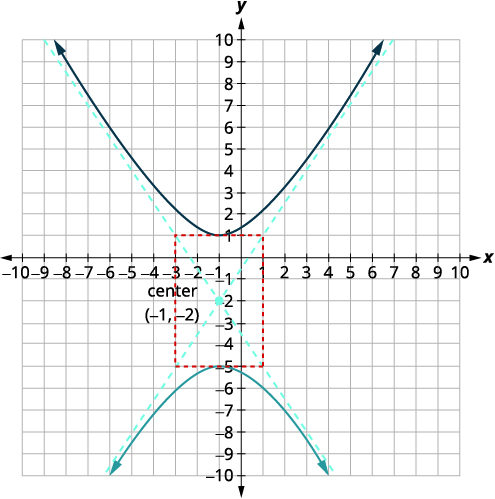
Графік\(\frac{(y+2)^{2}}{9}-\frac{(x+1)^{2}}{4}=1\).
Рішення:
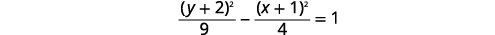 |
|
| Оскільки\(y^{2}\) -термін позитивний, гіпербола відкривається вгору і вниз. | 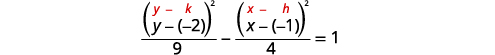 |
| Знайдіть центр,\((h,k)\). | Центр:\((-1,-2)\) |
| Знайти\(a,b\). | \(a=3 b=2\) |
| Намалюйте прямокутник, який проходить через точки\(3\) одиниць вище і нижче центру та \(2\) одиниць вліво/праворуч від центру. Намалюйте асимптоти—лінії через діагоналі прямокутника. Відзначте вершини. Графік гілок. |
 |
Графік\(\frac{(y+3)^{2}}{16}-\frac{(x+2)^{2}}{9}=1\).
- Відповідь
-
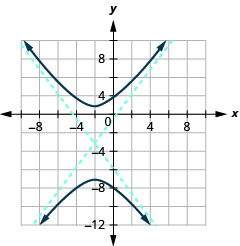
Малюнок 11.4.22
Графік\(\frac{(y+2)^{2}}{9}-\frac{(x+2)^{2}}{9}=1\).
- Відповідь
-
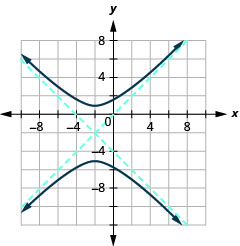
Малюнок 11.4.23
Знову ж таки, іноді нам доводиться ставити рівняння в стандартній формі як наш перший крок.
Запишіть рівняння в стандартній формі і графі\(4 x^{2}-9 y^{2}-24 x-36 y-36=0\).
Рішення:
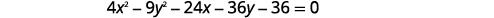 |
|
| Щоб дістатися до стандартної форми, заповніть квадрати. | 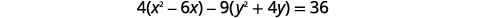 |
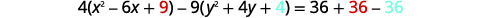 |
|
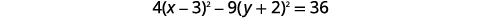 |
|
| Розділіть кожен член на\(36\), щоб отримати константу бути\(1\). | 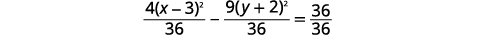 |
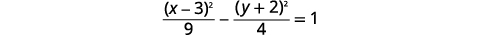 |
|
| Оскільки\(x^{2}\) -термін позитивний, гіпербола відкривається вліво і вправо. | |
| Знайдіть центр,\((h,k)\). | Центр:\((3, -2)\) |
| Знайти\(a,b\). |
\(a=3\) \(b=4\) |
| Намалюйте прямокутник, який проходить через точки\(3\) одиниць вліво/праворуч від центру та\(2\) одиниць вище та нижче центру. Намалюйте асимптоти—лінії через діагоналі прямокутника. Відзначте вершини. Графік гілок. |
 |
- Запишіть рівняння в стандартному вигляді і
- Графік\(9 x^{2}-16 y^{2}+18 x+64 y-199=0\).
- Відповідь
-
- \(\frac{(x+1)^{2}}{16}-\frac{(y-2)^{2}}{9}=1\)
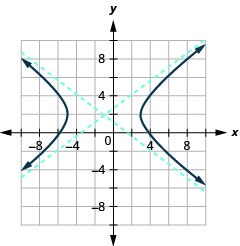
Малюнок 11.4.31
- Запишіть рівняння в стандартному вигляді і
- Графік\(16 x^{2}-25 y^{2}+96 x-50 y-281=0\).
- Відповідь
-
- \(\frac{(x+3)^{2}}{25}-\frac{(y+1)^{2}}{16}=1\)
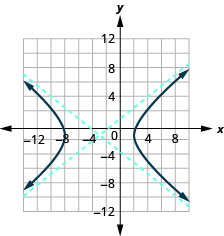
Малюнок 11.4.32
Визначити конічні перерізи за їх рівняннями
Тепер, коли ми завершили вивчення конічних перерізів, ми розглянемо різні рівняння і розпізнаємо деякі способи ідентифікації конічного конуса за його рівнянням. Коли нам дають рівняння до графіка, корисно визначити конічний, щоб ми знали, які наступні кроки потрібно зробити.
Ідентифікувати конічний з його рівняння простіше, якщо поставити змінні члени на одній стороні рівняння, а константи - на іншу.
| Конічна | Характеристика\(x^{2}\) - і\(y^{2}\) -термінів | Приклад |
|---|---|---|
| Парабола | \ (x^ {2}\) - і\(y^{2}\)\(x^{2}\) -Терми">Або\(y^{2}\). Тільки одна змінна знаходиться в квадраті. | \(x=3 y^{2}-2 y+1\) |
| Коло | \ (x^ {2}\) - і\(y^{2}\) -терміни">\(x^{2}\) - і\(y^{2}\) - члени мають однакові коефіцієнти. | \(x^{2}+y^{2}=49\) |
| Еліпс | \ (x^ {2}\) - і\(y^{2}\) -терміни">\(x^{2}\) - і\(y^{2}\) - члени мають один і той же знак, різні коефіцієнти. | \(4 x^{2}+25 y^{2}=100\) |
| Гіпербола | \ (x^ {2}\) - і\(y^{2}\) -терміни">\(x^{2}\) - і\(y^{2}\) - члени мають різні знаки, різні коефіцієнти. | \(25 y^{2}-4 x^{2}=100\) |
Визначте графік кожного рівняння як коло, параболу, еліпс або гіперболу.
- \(9 x^{2}+4 y^{2}+56 y+160=0\)
- \(9 x^{2}-16 y^{2}+18 x+64 y-199=0\)
- \(x^{2}+y^{2}-6 x-8 y=0\)
- \(y=-2 x^{2}-4 x-5\)
Рішення:
а.\(x^{2}\) - і\(y^{2}\) -терміни мають один і той же знак і різні коефіцієнти.
\(9 x^{2}+4 y^{2}+56 y+160=0\)
Еліпс
б.\(x^{2}\) - і\(y^{2}\) -терміни мають різні знаки і різні коефіцієнти.
\(9 x^{2}-16 y^{2}+18 x+64 y-199=0\)
Гіпербола
c\(x^{2}\) - і\(y^{2}\) -терміни мають однакові коефіцієнти.
\(x^{2}+y^{2}-6 x-8 y=0\)
Коло
d Тільки одна змінна,\(x\), знаходиться в квадраті.
\(y=-2 x^{2}-4 x-5\)
Парабола
Визначте графік кожного рівняння як коло, параболу, еліпс або гіперболу.
- \(x^{2}+y^{2}-8 x-6 y=0\)
- \(4 x^{2}+25 y^{2}=100\)
- \(y=6 x^{2}+2 x-1\)
- \(16 y^{2}-9 x^{2}=144\)
- Відповідь
-
- Коло
- Еліпс
- Парабола
- Гіпербола
Визначте графік кожного рівняння як коло, параболу, еліпс або гіперболу.
- \(16 x^{2}+9 y^{2}=144\)
- \(y=2 x^{2}+4 x+6\)
- \(x^{2}+y^{2}+2 x+6 y+9=0\)
- \(4 x^{2}-16 y^{2}=64\)
- Відповідь
-
- Еліпс
- Парабола
- Коло
- Гіпербола
Отримайте доступ до цих онлайн-ресурсів для отримання додаткових інструкцій та практики з гіперболами.
- Графік гіперболи з центром на початку
- Графік гіперболи з центром не біля початку
- Графік гіперболи в загальному вигляді
- Визначення конічних перерізів у загальному вигляді
Ключові поняття
- Гіпербола: Гіпербола - це всі точки на площині, де різниця їх відстаней від двох фіксованих точок постійна.
- Кожна з нерухомих точок називається вогнищем гіперболи.
Лінія, що проходить через вогнища, називається поперечною віссю.
Дві точки, де поперечна вісь перетинає гіперболу, є кожною вершиною гіперболи.
Середина сегмента, що приєднується до вогнищ, називається центром гіперболи.
Лінія, перпендикулярна поперечній осі, яка проходить через центр, називається сполученою віссю.
Кожен шматок графіка називається гілкою гіперболи.
Малюнок 11.4.2
Стандартні форми рівняння гіперболи з центром\((0,0)\)
| \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) | \(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\) | |
|---|---|---|
| Орієнтація | \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">Поперечна вісь на\(x\) -осі. Відкриває ліворуч і праворуч |
\ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">Поперечна вісь на\(y\) -осі. Відкриває вгору і вниз |
| Вершини | \ (\ розрив {x^ {2}} {a^ {2}} -\ розрив {y^ {2}} {b^ {2}} =1\) ">\((-a, 0),(a, 0)\) | \ (\ розрив {y^ {2}} {a^ {2}} -\ розрив {x^ {2}} {b^ {2}} =1\) ">\((0,-a),(0, a)\) |
| \(x\)-перехоплює | \ (\ розрив {x^ {2}} {a^ {2}} -\ розрив {y^ {2}} {b^ {2}} =1\) ">\((-a, 0),(a, 0)\) | \ (\ розрив {y^ {2}} {a^ {2}} -\ розрив {x^ {2}} {b^ {2}} =1\) ">немає |
| \(y\)-перехоплює | \ (\ розрив {x^ {2}} {a^ {2}} -\ розрив {y^ {2}} {b^ {2}} =1\) ">немає | \ (\ розрив {y^ {2}} {a^ {2}} -\ розрив {x^ {2}} {b^ {2}} =1\) ">\((0,-a),(0, a)\) |
| Прямокутник | \ (\ розрив {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">Використовувати\(( \pm a, 0)(0, \pm b)\) | \ (\ frac {y^ {2}} {a^ {2}} -\ розрив {x^ {2}} {b^ {2}} =1\) ">Використовувати\((0, \pm a)( \pm b, 0)\) |
| Асимптоти | \ (\ розрив {x^ {2}} {a^ {2}} -\ розрив {y^ {2}} {b^ {2}} =1\) ">\(y=\frac{b}{a} x, y=-\frac{b}{a} x\) | \ (\ розрив {y^ {2}} {a^ {2}} -\ розрив {x^ {2}} {b^ {2}} =1\) ">\(y=\frac{a}{b} x, y=-\frac{a}{b} x\) |
- Як графувати гіперболу в центрі\((0,0)\).
- Запишіть рівняння в стандартному вигляді.
- Визначте, горизонтальна або вертикальна поперечна вісь.
- Знайдіть вершини.
- Намалюйте прямокутник, центрований у початковій точці, що перетинає одну вісь,\(±a\) а іншу в\(±b\).
- Намалюйте асимптоти—лінії через діагоналі прямокутника.
- Намалюйте дві гілки гіперболи.
Стандартні форми рівняння гіперболи з центром\((h,k)\)
| \(\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1\) | \(\frac{(y-k)^{2}}{a^{2}}-\frac{(x-h)^{2}}{b^{2}}=1\) | |
|---|---|---|
| Орієнтація | \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">Поперечна вісь горизонтальна. Відкриває ліворуч і праворуч | \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">Поперечна вісь вертикальна. Відкриває вгору і вниз |
| Центр | \ (\ розрив {(x-h) ^ {2}} {a^ {2}} -\ розрив {(y-k) ^ {2}} {b^ {2}} =1\) ">\((h,k)\) | \ (\ розрив {(y-k) ^ {2}} {a^ {2}} -\ розрив {(x-h) ^ {2}} {b^ {2}} =1\) ">\((h,k)\) |
| Вершини | \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">\(a\) одиниці ліворуч і праворуч від центру | \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">\(a\) одиниці вище і нижче центру |
| Прямокутник | \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">Використовуйте\(a\) одиниці вліво/праворуч від центральних\(b\) одиниць над/нижче центру | \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">Використовуйте\(a\) одиниці над/нижче центральних\(b\) одиниць ліво/праворуч від центру |
- Як графувати гіперболу в центрі\((h,k)\).
- Запишіть рівняння в стандартному вигляді.
- Визначте, горизонтальна або вертикальна поперечна вісь.
- Знайдіть центр і\(a,b\).
- Намалюйте прямокутник по центру\((h,k)\) за допомогою\(a,b\).
- Намалюйте асимптоти—лінії через діагоналі прямокутника. Відзначте вершини.
- Намалюйте дві гілки гіперболи.
| Конічна | Характеристика\(x^{2}\) - і\(y^{2}\) -термінів | Приклад |
|---|---|---|
| Парабола | \ (x^ {2}\) - і\(y^{2}\)\(x^{2}\) -Терми">Або\(y^{2}\). Тільки одна змінна знаходиться в квадраті. | \(x=3 y^{2}-2 y+1\) |
| Коло | \ (x^ {2}\) - і\(y^{2}\) -терміни">\(x^{2}\) - і\(y^{2}\) - члени мають однакові коефіцієнти. | \(x^{2}+y^{2}=49\) |
| Еліпс | \ (x^ {2}\) - і\(y^{2}\) -терміни">\(x^{2}\) - і\(y^{2}\) - члени мають один і той же знак, різні коефіцієнти. | \(4 x^{2}+25 y^{2}=100\) |
| Гіпербола | \ (x^ {2}\) - і\(y^{2}\) -терміни">\(x^{2}\) - і\(y^{2}\) - члени мають різні знаки, різні коефіцієнти. | \(25 y^{2}-4 x^{2}=100\) |
Глосарій
- гіпербола
- Гіпербола визначається як всі точки на площині, де різниця їх відстаней від двох фіксованих точок постійна.
