Skip to main content
LibreTexts - Ukrayinska

11.4: Еліпси

  1. Last updated
  2. Save as PDF
  • Page ID
    59825

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    До кінця цього розділу ви зможете:

    • Графік еліпса з центром у початку
    • Знайти рівняння еліпса з центром у початку
    • Графік еліпса з центром, який не знаходиться біля початку
    • Розв'яжіть додаток з еліпсами

    Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

    1. Графік\(y=(x-1)^{2}-2\) з використанням перетворень.
      Якщо ви пропустили цю проблему, перегляньте приклад 9.57.
    2. Завершіть квадрат:\(x^{2}-8 x=8\).
      Якщо ви пропустили цю проблему, перегляньте приклад 9.12.
    3. Пишіть в стандартній формі. \(y=2 x^{2}-12 x+14\)
      Якщо ви пропустили цю проблему, перегляньте приклад 9.59.

    Графік еліпса з центром біля початку

    Наступний конічний розріз, який ми розглянемо, - це еліпс. Ми визначаємо еліпс як усі точки на площині, де сума відстаней від двох фіксованих точок є постійною. Кожна з заданих точок називається фокусом еліпса.

    Визначення\(\PageIndex{1}\)

    Еліпс - це всі точки на площині, де сума відстаней від двох фіксованих точок є постійною. Кожна з нерухомих точок називається фокусом еліпса.

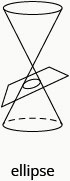
    На цьому малюнку зображений подвійний конус, перетинається площиною з утворенням еліпса.
    Малюнок 11.3.1

    Ми можемо намалювати еліпс, взявши певну фіксовану довжину гнучкої рядки і прикріпивши кінці до двох мініатюр. Використовуємо ручку, щоб натягнути струну туго і обертати її навколо двох мініатюр. Фігура, яка виходить, є еліпсом.

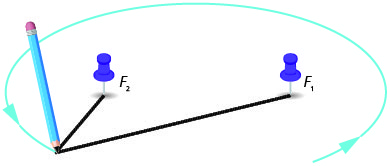
    На цьому малюнку зображена ручка, прикріплена до двох струн, інші кінці яких прикріплені до двох пальцях. Струни натягуються туго, а ручка обертається, щоб намалювати еліпс. Мініатки позначені F індексу 1 і F індексу 2.
    Малюнок 11.3.2

    Лінія, проведена через осередки, перетинає еліпс в двох точках. Кожна точка називається вершиною еліпса. Відрізок, що з'єднує вершини, називається великою віссю. Середина відрізка називається центром еліпса. Відрізок, перпендикулярний великій осі, який проходить через центр і перетинає еліпс у двох точках, називається другорядною віссю.

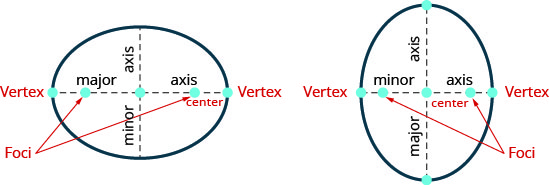
    На цьому малюнку зображено два еліпса. У кожній дві точки в межах еліпса позначені вогнищами. Лінія, проведена через осередки, перетинає еліпс в двох точках. Кожна точка позначається вершиною. На малюнку зліва відрізок, що з'єднує вершини, називається великою віссю. Відрізок, перпендикулярний до великої осі, який проходить через середину і перетинає еліпс у двох точках, позначається незначною віссю. Велика вісь довша за малу вісь. На малюнку праворуч відрізок через вогнища, що з'єднує вершини, коротше і позначений другорядною віссю. Його середина позначена центром.
    Малюнок 11.3.3

    Раніше ми згадували, що наша мета полягає в тому, щоб з'єднати геометрію конічного конуса з алгеброю. Розміщення еліпса на прямокутній системі координат дає нам таку можливість. На малюнку ми розмістили еліпс так, щоб осередки\(((−c,0),(c,0))\) знаходилися на\(x\) -осі, а центр - початок.

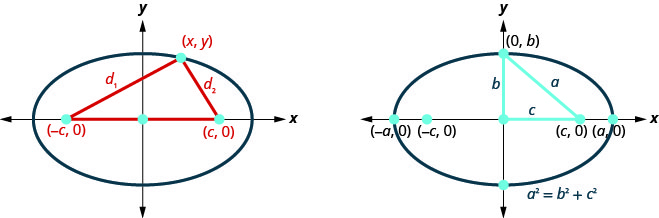
    На малюнку зліва зображений еліпс з центром у початку координатних осей і його осередками в точках мінус (c, 0) і (c, 0). Відрізок з'єднується (від'ємний c, 0) з точкою (x, y) на еліпсі. Відрізок позначений d індексом 1. Інший сегмент, позначений d індексом 2, з'єднує (c, 0) до (x, y). На малюнку праворуч зображено еліпс з центром у початку, вогнищами (від'ємним c, 0) та (c, 0) та вершинами (від'ємний a, 0) та (a, 0). Точка, де еліпс перетинає вісь y, позначається (0, b). Відрізки, що з'єднуються (0, 0) до (c, 0), (c, 0) до (0, b) і (0, b) до (0, 0) утворюють щільний кутовий трикутник зі сторонами c, a і b відповідно. Рівняння є квадратом дорівнює b в квадраті плюс c в квадраті.
    Малюнок 11.3.4

    Визначення стверджує, що сума відстані від вогнищ до точки\((x,y)\) є постійною. Так\(d_{1}+d_{2}\) це константа, яку ми будемо називати\(2a\) так,\(d_{1}+d_{2}=2 a\). Ми будемо використовувати формулу відстані, щоб привести нас до алгебраїчної формули для еліпса.

    \(d_{1} \quad+\quad \quad d_{2} \quad=\quad 2 a\)

    Використовуйте формулу відстані, щоб знайти\(d_{1},d_{2}\).

    \(\sqrt{(x-(-c))^{2}+(y-0)^{2}}+\sqrt{(x-c)^{2}+(y-0)^{2}}=2 a\)

    Після усунення радикалів і спрощення отримуємо:

    \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{a^{2}-c^{2}}=1\)

    Щоб спростити рівняння еліпса, дозволимо\(a^{2}−c^{2}=b^{2}\) .Отже, рівняння еліпса з центром у початку в стандартному вигляді таке:

    \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)

    Для побудови графіка еліпса буде корисно знати перехоплення. Ми знайдемо\(x\) -перехоплення і\(y\) -перехоплення за формулою.

    \(y\)-перехоплює

    Нехай\(x=0\).

    \(\begin{aligned} \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} &=1 \\ \frac{0^{2}}{a^{2}}+\frac{y^{2}}{a^{2}} &=1 \\ \frac{y^{2}}{b^{2}} &=1 \\ y^{2} &=b^{2} \\ y &=\pm b \end{aligned}\)

    \(y\)-перехоплює є\((0,b)\) і\((0, -b)\).

    \(x\)-перехоплює

    Нехай\(y=0\).

    \(\begin{aligned} \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}}+\frac{0^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}} &=1 \\ x^{2} &=a^{2} \\ x &=\pm a \end{aligned}\)

    \(x\)-перехоплює є\((a,0)\) і\((-a,0)\).

    Визначення\(\PageIndex{2}\)

    Стандартна форма рівняння еліпса з центром\((0,0)\)

    Стандартна форма рівняння еліпса з центром\((0,​​0)\), є

    \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)

    \(x\)-перехоплює є\((a,0)\) і\((−a,0)\).

    \(y\)-перехоплює є\((0,b)\) і\((0,−b)\).

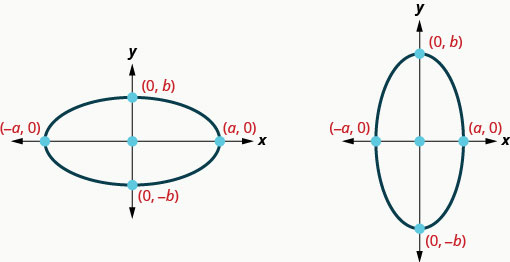
    Дві фігури показують еліпси з їх центрами на початку координатних осей. Вони перетинають вісь x в точках (від'ємний a, 0) і (a, 0) і вісь y в точках (0, b) і (0, від'ємний b). На малюнку зліва велика вісь еліпса знаходиться вздовж осі х, а на малюнку праворуч - уздовж осі y.
    Малюнок 11.3.5

    Зверніть увагу, що коли велика вісь горизонтальна, значення\(a\) буде більше, ніж значення\(b\) і коли велика вісь вертикальна, значення\(b\) буде більше, ніж значення\(a\). Ми будемо використовувати цю інформацію для графіка еліпса, який зосереджений на початку.

    Еліпс з центром\((0,0)\)

    \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) \(a>b\) \(b>a\)
    Велика вісь на\(x\) -осі. на\(y\) -осі
    \(x\)-перехоплює \((-a, 0),(a, 0)\)  
    \(y\)-перехоплює \((0,-b),(0, b)\)  
    Таблиця 11.3.1
    Приклад\(\PageIndex{1}\)

    Графік:\(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\).

    Рішення:

    Крок 1. Запишіть рівняння в стандартному вигляді. Він знаходиться в стандартному вигляді. \(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\)
    Крок 2. Визначте, чи є велика вісь горизонтальною або вертикальною. Оскільки\(9>4\) і\(9\) знаходиться в\(y^{2}\) терміні, то велика вісь вертикальна. Велика вісь вертикальна.
    Крок 3. Знайдіть кінцеві точки великої осі.

    Кінцевими точками будуть\(y\) -перехоплення.

    З тих пір\(b^{2}=9\)\(b=\pm 3\).

    Кінцеві точки великої осі є\((0,3),(0,-3)\).

    		 Кінцеві точки великої осі є\((0,3),(0,-3)\).
    Крок 4. Знайдіть кінцеві точки другорядної осі. Кінцевими точками будуть\(x\) -перехоплення.

    З тих пір\(a^{2}=4\)\(a=\pm 2\).

    Кінцеві точки великої осі є\((2,0),(-2,0)\).

    		 Кінцеві точки великої осі є\((2,0),(-2,0)\).
    Крок 5. Намалюйте еліпс.   Скріншот (147) .png
    Таблиця 11.3.2
    Вправа\(\PageIndex{1}\)

    Графік:\(\frac{x^{2}}{4}+\frac{y^{2}}{16}=1\).

    Відповідь
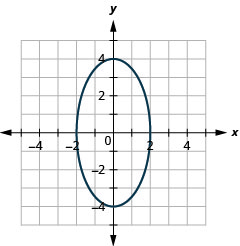
    Цей графік показує еліпс з перехопленнями x (від'ємні 2, 0) і (2, 0) і y перехоплює (0, 4) і (0, негативний 4).
    Малюнок 11.3.7
    Вправа\(\PageIndex{2}\)

    Графік:\(\frac{x^{2}}{9}+\frac{y^{2}}{16}=1\).

    Відповідь
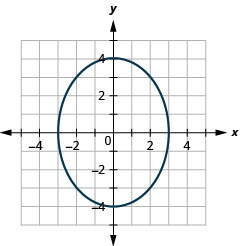
    Цей графік показує еліпс з перехопленнями x (від'ємні 3, 0) і (3, 0) і y перехоплює (0, 4) і (0, негативний 4).
    Малюнок 11.3.8

    Підсумовуємо кроки для довідки.

    ЯК НАМАЛЮВАТИ ЕЛІПС З ЦЕНТРОМ\((0,0)\).

    1. Запишіть рівняння в стандартному вигляді.
    2. Визначте, чи є велика вісь горизонтальною або вертикальною.
    3. Знайдіть кінцеві точки великої осі.
    4. Знайти кінцеві точки другорядної осі
    5. Намалюйте еліпс.

    Іноді наше рівняння спочатку потрібно поставити в стандартному вигляді.

    Приклад\(\PageIndex{2}\)

    Графік\(x^{2}+4 y^{2}=16\).

    Рішення:

    Ми визнаємо це рівнянням
    еліпса, оскільки обидва\(x\) і\(y\) члени
    квадратні і мають різні коефіцієнти.    		 \(x^{2}+4 y^{2}=16\)
    Щоб отримати рівняння в стандартному вигляді, розділіть
    обидві сторони на\(16\) так, щоб рівняння
    дорівнювало\(1\).    		 \(\frac{x^{2}}{16}+\frac{4 y^{2}}{16}=\frac{16}{16}\)
    Спростити. \(\frac{x^{2}}{16}+\frac{y^{2}}{4}=1\)
    Рівняння знаходиться в стандартній формі.
    Еліпс зосереджений у початковій точці.    		 Центр - це\((0,0)\).
    Оскільки\(16>4\) і\(16\) знаходиться в\(x^{2}\) терміні,
    то велика вісь горизонтальна.    		  
    \(a^{2}=16, a=\pm 4\)
    \(b^{2}=4, \quad b=\pm 2\)
    Вершини є\((4,0),(−4,0)\).
    Кінцеві точки другорядної осі є
    \((0,2),(0,−2)\).
    Намалюйте параболу. .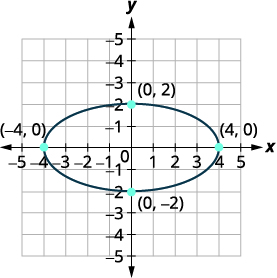
    Таблиця 11.3.3
    Вправа\(\PageIndex{3}\)

    Графік\(9 x^{2}+16 y^{2}=144\).

    Відповідь
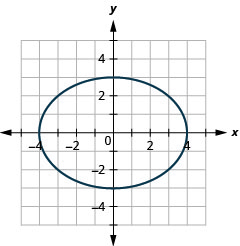
    Цей графік показує еліпс з перехопленнями x (від'ємні 4, 0) і (4, 0) і y перехоплює (0, 3) і (0, негативний 3).
    Малюнок 11.3.10
    Вправа\(\PageIndex{4}\)

    Графік\(16 x^{2}+25 y^{2}=400\).

    Відповідь
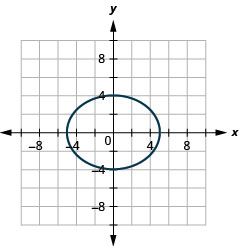
    Цей графік показує еліпс з перехопленнями x (від'ємні 5, 0) і (5, 0) і y перехоплює (0, 4) і (0, негативний 4).
    Малюнок 11.3.11

    Знайти рівняння еліпса з центром біля початку

    Якщо нам задано графік еліпса, ми можемо знайти рівняння еліпса.

    Приклад\(\PageIndex{3}\)

    Знайдіть рівняння показаного еліпса.

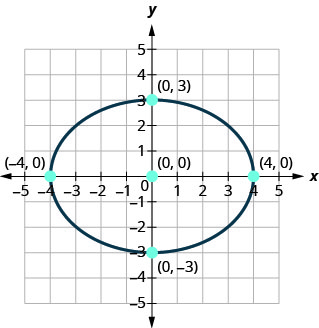
    Цей графік показує еліпс з перехопленнями x (від'ємні 4, 0) і (4, 0) і y перехоплює (0, 3) і (0, негативний 3).
    Малюнок 11.3.12

    Рішення:

    Ми визнаємо це як еліпс, який зосереджений на початку.

    \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)

    Оскільки велика вісь горизонтальна, а відстань від центру до вершини є\(4\), ми знаємо\(a=4\) і так\(a^{2}=16\).

    \(\frac{x^{2}}{16}+\frac{y^{2}}{b^{2}}=1\)

    Мала вісь вертикальна і відстань від центру до еліпса є\(3\), ми знаємо\(b=3\) і так\(b^{2}=9\).

    \(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\)

    Вправа\(\PageIndex{5}\)

    Знайдіть рівняння показаного еліпса.

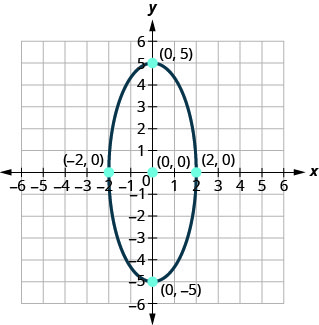
    Цей графік показує еліпс з перехопленнями x (від'ємні 2, 0) і (2, 0) і y перехоплює (0, 5) і (0, негативний 5).
    Малюнок 11.3.13
    Відповідь

    \(\frac{x^{2}}{4}+\frac{y^{2}}{25}=1\)

    Вправа\(\PageIndex{6}\)

    Знайдіть рівняння показаного еліпса.

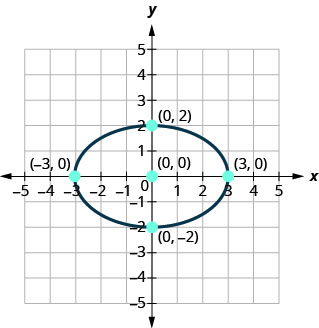
    Цей графік показує еліпс з перехопленнями x (від'ємні 3, 0) і (3, 0) і y перехоплює (0, 2) і (0, негативний 2).
    Малюнок 11.3.14
    Відповідь

    \(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\)

    Графік еліпса з центром не біля початку

    Еліпси, які ми розглядали досі, були зосереджені на початку. Зараз ми розглянемо еліпси, центр яких є\((h,k)\).

    Рівняння є\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\) і коли\(a>b\), велика вісь горизонтальна, тому відстань від центру до вершини становить\(a\). Коли\(b>a\), велика вісь вертикальна, тому відстань від центру до вершини становить\(b\).

    Визначення\(\PageIndex{3}\)

    Стандартна форма рівняння еліпса з центром\((h,k)\)

    Стандартна форма рівняння еліпса з центром\((h,k)\), є

    \(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\)

    Коли\(a>b\), велика вісь горизонтальна, тому відстань від центру до вершини становить\(a\).

    Коли\(b>a\), велика вісь вертикальна, тому відстань від центру до вершини становить\(b\).

    Приклад\(\PageIndex{4}\)

    Графік:\(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\).

    Рішення:

    Рівняння знаходиться в стандартній формі,\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\). \(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\)
    Еліпс знаходиться в центрі\((h,k)\). Центр - це\((3,1)\).
    Оскільки\(9>4\) і\(9\) знаходиться в\(x^{2}\) терміні, то велика вісь горизонтальна.  
    \(a^{2}=9, a=\pm 3\)
    \(b^{2}=4, b=\pm 2\)    		 Відстань від центру до вершин дорівнює\(3\).
    Відстань від центру до кінцевих точок
    другорядної осі дорівнює\(2\).
    Намалюйте еліпс. .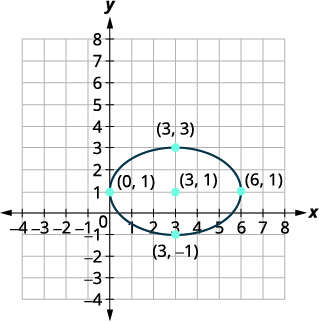
    Таблиця 11.3.4
    Вправа\(\PageIndex{7}\)

    Графік:\(\frac{(x+3)^{2}}{4}+\frac{(y-5)^{2}}{16}=1\).

    Відповідь
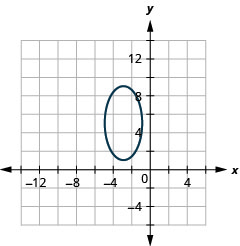
    Цей графік показує еліпс з центром в (від'ємний 3, 5), вершинами в (від'ємний 3, 9) і (від'ємний 3, 1) і кінцевими точками другорядної осі в (від'ємні 5, 5) і (від'ємні 1, 5).
    Малюнок 11.3.16
    Вправа\(\PageIndex{8}\)

    Графік:\(\frac{(x-1)^{2}}{25}+\frac{(y+3)^{2}}{16}=1\).

    Відповідь
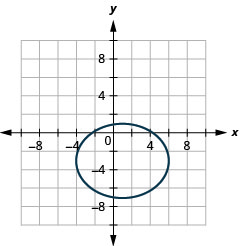
    Цей графік показує еліпс з центром у 1, від'ємним 3, вершинами в (від'ємний 4, негативний 3) і (6, негативний 3) і кінцеві точки другорядної осі в 1, 1) і (негативний 1, негативний 7).
    Малюнок 11.3.17

    Якщо ми подивимося на рівняння\(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\) і\(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\), то побачимо, що вони обидва еліпси з\(a=3\) і\(b=2\). Так вони будуть мати однаковий розмір і форму. Вони відрізняються тим, що не мають однакового центру.

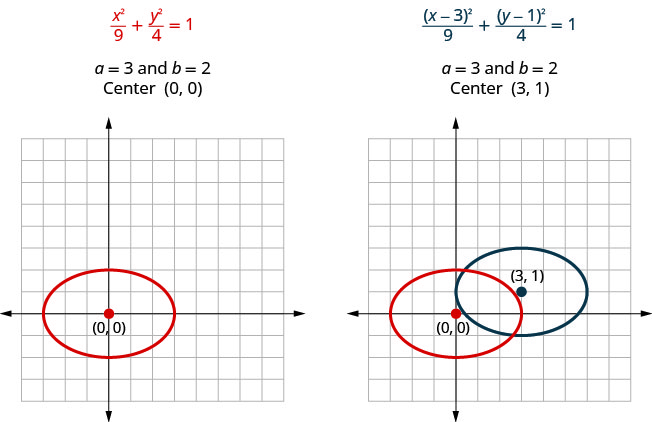
    Рівняння на першому малюнку дорівнює x у квадраті на 9 плюс y в квадраті на 4 дорівнює 1. Тут a дорівнює 3, а b - 2. Еліпс зображено на графіку з центром (0, 0). Рівняння праворуч є відкритими дужками х мінус 3 закрити дужки в квадраті на 9 плюс відкриті дужки y мінус 1 закрити дужки в квадраті на 4 дорівнює 1. Тут теж a дорівнює 3 і b дорівнює 2, але центр - (3, 1). Еліпс показаний на тому ж графіку разом з першим еліпсом. Показано, що центр перемістився 3 одиниці вправо і 1 блок вгору.
    Малюнок 11.3.18

    Зверніть увагу на графіку вище, що ми могли б графікувати\(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\) перекладами. Ми перемістили оригінальний еліпс на праві\(3\) одиниці, а потім вгору\(1\) одиниці.

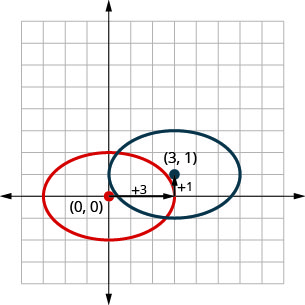
    Цей графік показує еліпс, перекладений з центру (0, 0) до центру (3, 1). Центр перемістився 3 одиниці вправо і 1 блок вгору. Оригінальний еліпс має вершини в (від'ємні 3, 0) і (3, 0) і кінцеві точки другорядної осі в (від'ємний 2, 0) і (2, 0). Перекладений еліпс має вершини в (0, 1) і (6, 1) і кінцеві точки другорядної осі в (3, від'ємний 1) і (3, 3).
    Малюнок 11.3.19

    У наступному прикладі ми будемо використовувати метод перекладу для графування еліпса.

    Приклад\(\PageIndex{5}\)

    Графік\(\frac{(x+4)^{2}}{16}+\frac{(y-6)^{2}}{9}=1\) за перекладом.

    Рішення:

    Цей еліпс матиме той самий розмір і форму, що і центр\(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\) якого\((0,0)\). Спочатку ми графуємо цей еліпс.

    Центр - це\((0,0)\). Центр\((0,0)\)
    Так як\(16>9\), велика вісь горизонтальна.  
    \(a^{2}=16, a=\pm 4\)
    \(b^{2}=9, \quad b=\pm 3\)    		 Вершини є\((4,0),(−4,0)\).
    Кінцеві точки другорядної осі є
    \((0,3),(0,−3)\).
    Намалюйте еліпс. .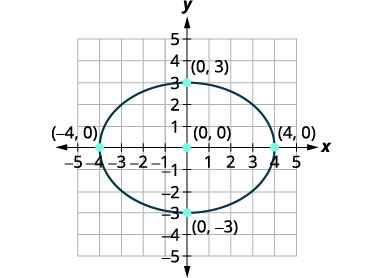
    Вихідне рівняння знаходиться в стандартній формі,\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\). \(\frac{(x-(-4))^{2}}{16}+\frac{(y-6)^{2}}{9}=1\)
    Еліпс знаходиться в центрі\((h,k)\). Центр - це\((-4,6)\).
    Переводимо графік з\(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\) чотирьох
    одиниць вліво, а потім вгору\(6\) одиниць.
    Переконайтеся, що центр є\((−4,6)\).
    Новий еліпс - це еліпс, рівняння якого
    є
    \(\frac{(x+4)^{2}}{16}+\frac{(y-6)^{2}}{9}=1\).    		 .
    Таблиця 11.3.5
    Вправа\(\PageIndex{9}\)

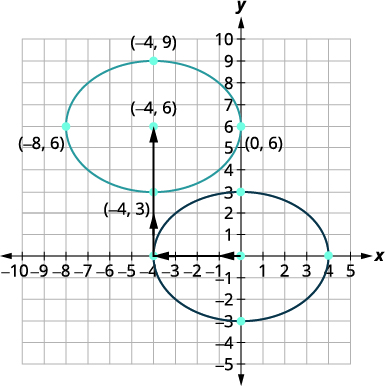    Графік\(\frac{(x-5)^{2}}{9}+\frac{(y+4)^{2}}{4}=1\) за перекладом.

    Відповідь
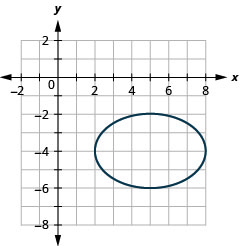
    Цей графік показує еліпс з центром (5, від'ємний 4), вершинами (2, від'ємним 4) і (8, негативним 4) і кінцевими точками другорядної осі (5, від'ємний 2) і (5, негативний 6).
    Малюнок 11.3.22
    Вправа\(\PageIndex{10}\)

    Графік\(\frac{(x+6)^{2}}{16}+\frac{(y+2)^{2}}{25}=1\) за перекладом.

    Відповідь
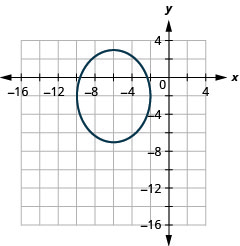
    Цей графік показує еліпс з центром (від'ємний 6, від'ємний 2), вершинами (від'ємний 6, 3) і (від'ємний 6, від'ємний 7) і кінцевими точками другорядної осі (від'ємний 10, від'ємний 2) і (від'ємний 2, негативний 2).
    Малюнок 11.3.23

    Коли рівняння має як a, так\(x^{2}\) і a\(y^{2}\) з різними коефіцієнтами, ми перевіряємо, що це крапка, поставивши його в стандартну форму. Потім ми зможемо скласти графік рівняння.

    Приклад\(\PageIndex{6}\)

    Запишіть рівняння\(x^{2}+4 y^{2}-4 x+24 y+24=0\) в стандартній формі і графі.

    Рішення:

    Ставимо рівняння в стандартному вигляді, заповнивши квадрати в обох\(x\) і\(y\).

      \(x^{2}+4 y^{2}-4 x+24 y+24=0\)
    Перепишіть групування\(x\) термінів і\(y\) термінів. .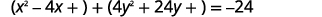
    Зробіть коефіцієнти рівними\(x^{2}\) і\(y^{2}\) рівними\(1\). .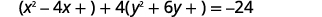
    Завершіть квадрати. .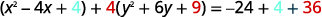
    Запишіть як біноміальні квадрати. .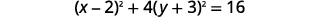
    Розділіть обидві сторони на\(16\), щоб отримати\(1\) праворуч. .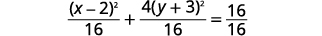
    Спростити. .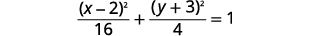
    Рівняння в стандартній формі,\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\) .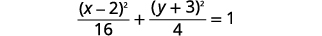
    Еліпс знаходиться в центрі\((h,k)\). Центр - це\((2,-3)\).

    Оскільки\(16>4\) і\(16\) знаходиться в\(x^{2}\) терміні, то велика вісь горизонтальна.

    \(a^{2}=16, a=\pm 4\)
    \(b^{2}=4, \quad b=\pm 2\)

    Відстань від центру до вершин дорівнює\(4\).

    Відстань від центру до кінцевих точок другорядної осі дорівнює\(2\).
    Намалюйте еліпс. .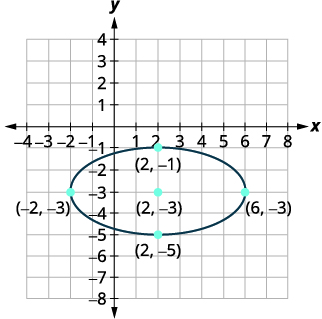
    Таблиця 11.3.6
    Вправа\(\PageIndex{11}\)
    1. Запишіть рівняння\(6 x^{2}+4 y^{2}+12 x-32 y+34=0\) в стандартному вигляді і
    2. Графік.
    Відповідь
    1. \(\frac{(x+1)^{2}}{6}+\frac{(y-4)^{2}}{9}=1\)
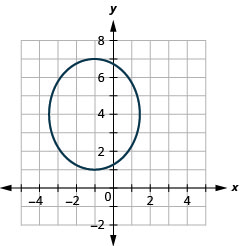
    Цей графік показує еліпс з центром (від'ємний 1, 4), вершинами мінус (1, 1) і (від'ємний 1, 7) і кінцевими точками другорядної осі приблизно (від'ємні 3,5, 4) і (приблизно 1,5, 4).
    Малюнок 11.3.32
    Вправа\(\PageIndex{12}\)
    1. Запишіть рівняння\(4 x^{2}+y^{2}-16 x-6 y+9=0\) в стандартному вигляді і
    2. Графік.
    Відповідь
    1. \(\frac{(x-2)^{2}}{4}+\frac{(y-3)^{2}}{16}=1\)
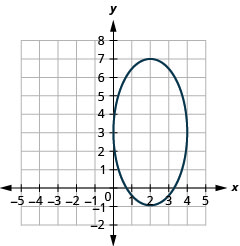
    Цей графік показує еліпс з центром (2, 3), вершинами (2, від'ємними 1) і (2, 7) і кінцевими точками другорядної осі (0, 3) і (4, 3).
    Малюнок 11.3.33

    Вирішити додаток з еліпсами

    Орбіти планет навколо Сонця слідують еліптичними шляхами.

    Приклад\(\PageIndex{7}\)

    Плутон (карликова планета) рухається по еліптичній орбіті навколо Сонця. Найближчий Плутон потрапляє до\(30\) Сонця приблизно астрономічних одиниць (АС), а найдальший - приблизно\(50\) AU. Сонце є одним з вогнищ еліптичної орбіти. Допустивши центр еліпса у початку та маркування осей в АС, орбіта буде виглядати як на малюнку нижче. Використовуйте графік, щоб написати рівняння для еліптичної орбіти Плутона.

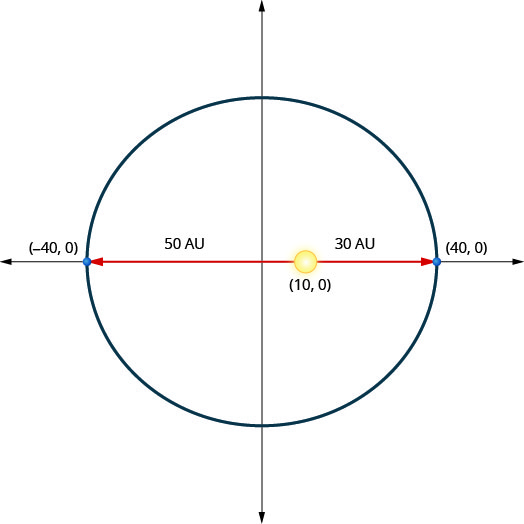
    Цей графік показує еліпс з центром (0, 0) і вершинами (від'ємні 40, 0) і (40, 0). Сонце показано в точці (10, 0). Це 30 одиниць від правої вершини і 50 одиниць від лівої вершини.
    Малюнок 11.3.34

    Рішення:

    Ми визнаємо це як еліпс, який зосереджений на початку.

    \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)

    Оскільки велика вісь горизонтальна, а відстань від центру до вершини є\(40\), ми знаємо\(a=40\) і так\(a^{2}=1600\).

    \(\frac{x^{2}}{1600}+\frac{y^{2}}{b^{2}}=1\)

    Мала вісь вертикальна, але кінцеві точки не задані. Щоб знайти,\(b\) ми будемо використовувати розташування Сонця. Оскільки Сонце є фокусом еліпса в точці\((10,0)\), ми знаємо\(c=10\). Використовуйте це, щоб вирішити для\(b^{2}\).

    \(b^{2}=a^{2}-c^{2}\)
    \(b^{2}=40^{2}-10^{2}\)
    \(b^{2}=1600-100\)
    \(b^{2}=1500\)

    \(b^{2}\)Підставляємо\(a^{2}\) і в стандартну форму еліпса.

    \(\frac{x^{2}}{1600}+\frac{y^{2}}{1500}=1\)

    Вправа\(\PageIndex{13}\)

    Планета рухається по еліптичній орбіті навколо свого сонця. Найближча планета потрапляє до Сонця приблизно\(20\) AU, а найдальша - приблизно\(30\) AU. Сонце є одним з вогнищ еліптичної орбіти. Допустивши центр еліпса у початку та маркування осей в АС, орбіта буде виглядати як на малюнку нижче. Використовуйте графік, щоб написати рівняння для еліптичної орбіти планети.

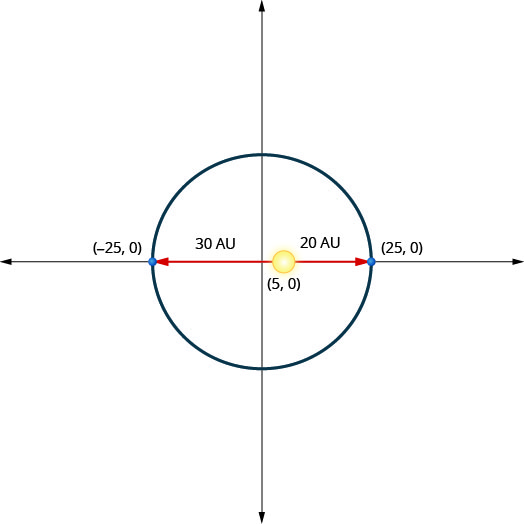
    Цей графік показує еліпс з центром (0, 0) і вершинами (від'ємні 25, 0) і (25, 0). Сонце показано в точці (5, 0). Це 20 одиниць від правої вершини і 30 одиниць від лівої вершини.
    Малюнок 11.3.35
    Відповідь

    \(\frac{x^{2}}{625}+\frac{y^{2}}{600}=1\)

    Вправа\(\PageIndex{14}\)

    Планета рухається по еліптичній орбіті навколо свого сонця. Найближча планета потрапляє до Сонця приблизно\(20\) AU, а найдальша - приблизно\(50\) AU. Сонце є одним з вогнищ еліптичної орбіти. Допустивши центр еліпса у початку та маркування осей в АС, орбіта буде виглядати як на малюнку нижче. Використовуйте графік, щоб написати рівняння для еліптичної орбіти планети.

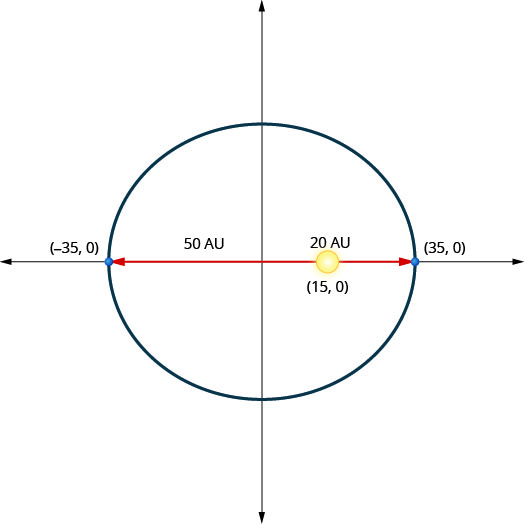
    Цей графік показує еліпс з центром (0, 0) і вершинами (від'ємні 35, 0) і (35, 0). Сонце показано в точці (15, 0). Це 20 одиниць від правої вершини і 50 одиниць від лівої вершини.
    Малюнок 11.3.36
    Відповідь

    \(\frac{x^{2}}{1225}+\frac{y^{2}}{1000}=1\)

    Отримайте доступ до цих онлайн-ресурсів для отримання додаткових інструкцій та практики з еліпсами.

    • Конічні перерізи: Графічні еліпси Частина 1
    • Конічні перерізи: Графічні еліпси Частина 2
    • Рівняння для еліпса з графа

    Ключові концепції

    • Еліпс: Еліпс - це всі точки на площині, де сума відстаней від двох фіксованих точок є постійною. Кожна з нерухомих точок називається фокусом еліпса.
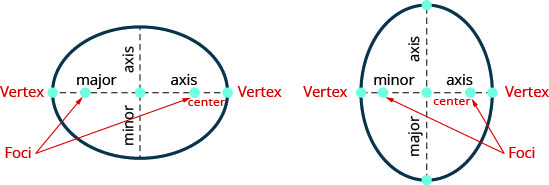
      На цьому малюнку зображено два еліпса. У кожній дві точки в межах еліпса позначені вогнищами. Лінія, проведена через осередки, перетинає еліпс в двох точках. Кожна точка позначається вершиною. На малюнку зліва відрізок, що з'єднує вершини, називається великою віссю. Відрізок, перпендикулярний до великої осі, який проходить через середину і перетинає еліпс у двох точках, позначається незначною віссю. Велика вісь довша за малу вісь. На малюнку праворуч відрізок через вогнища, що з'єднує вершини, коротше і позначений другорядною віссю. Його середина позначена центром.

    Малюнок 11.3.37

    • Якщо провести лінію через вогнища, перетинає еліпс у двох точках - кожна з них називається вершиною еліпса.
      Відрізок, що з'єднує вершини, називається великою віссю.
      Середина відрізка називається центром еліпса.
      Відрізок, перпендикулярний великій осі, який проходить через центр і перетинає еліпс у двох точках, називається другорядною віссю.
    • Стандартна форма рівняння еліпса з центром\((0,0)\): стандартна форма рівняння еліпса з центром\((0,0)\), є

      \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)

      \(x\)-перехоплює є\((a,0)\) і\((−a,0)\).
      \(y\)-перехоплює є\((0,b)\) і\((0,−b)\).
    • Як створити еліпс з центром\((0,0)\)
      1. Запишіть рівняння в стандартному вигляді.
      2. Визначте, чи є велика вісь горизонтальною або вертикальною.
      3. Знайдіть кінцеві точки великої осі.
      4. Знайти кінцеві точки другорядної осі
      5. Намалюйте еліпс.
    • Стандартна форма рівняння еліпса з центром\((h,k)\): стандартна форма рівняння еліпса з центром\((h,k)\), є

      \(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\)

      Коли\(a>b\), велика вісь горизонтальна, тому відстань від центру до вершини становить\(a\).
      Коли\(b>a\), велика вісь вертикальна, тому відстань від центру до вершини становить\(b\).

    Глосарій

    еліпс
    Еліпс - це всі точки на площині, де сума відстаней від двох фіксованих точок є постійною.