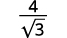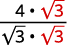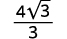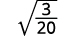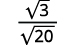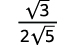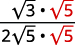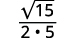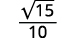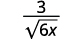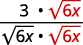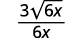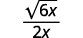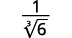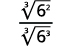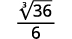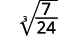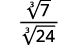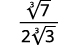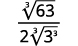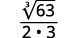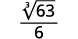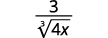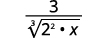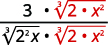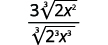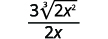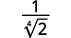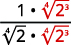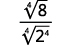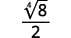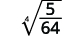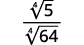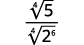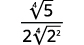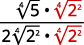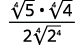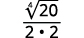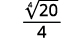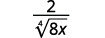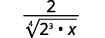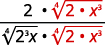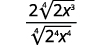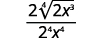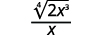8.6: Розділіть радикальні вирази
- Page ID
- 59629
До кінця цього розділу ви зможете:
- Розділити радикальні вирази
- Раціоналізувати знаменник на один термін
- Раціоналізувати двочленний знаменник
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Спростити:\(\dfrac{30}{48}\).
Якщо ви пропустили цю проблему, перегляньте приклад 1.24. - Спростити:\(x^{2}⋅x^{4}\).
Якщо ви пропустили цю проблему, перегляньте приклад 5.12. - Помножити:\((7+3x)(7−3x)\).
Якщо ви пропустили цю проблему, перегляньте приклад 5.32.
Розділити радикальні вирази
Ми використали часткову властивість радикальних виразів для спрощення коренів дробів. Нам потрібно буде використовувати цю властивість «навпаки», щоб спростити дріб з радикалами. Ми знову даємо частку властивість радикальних виразів для зручності довідки. Пам'ятайте, ми припускаємо, що всі змінні більше або рівні нулю, так що не потрібні бари абсолютних значень.
Визначення\(\PageIndex{1}\): Quotient Property of Radical Expressions
Якщо\(\sqrt[n]{a}\) і\(\sqrt[n]{b}\) є дійсними числами\(b≠0\), і для будь-якого цілого числа\(n≥2\) тоді,
\(\sqrt[n]{\dfrac{a}{b}}=\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}} \quad \text { and } \quad \dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\dfrac{a}{b}}\)
Ми будемо використовувати часткову властивість радикальних виразів, коли дріб, з якого ми починаємо, є часткою двох радикалів, і жоден радикальний не є ідеальною силою індексу. Коли ми пишемо дріб одним радикалом, ми можемо знайти спільні множники в чисельнику та знаменнику.
Спростити:
- \(\dfrac{\sqrt{72 x^{3}}}{\sqrt{162 x}}\)
- \(\dfrac{\sqrt[3]{32 x^{2}}}{\sqrt[3]{4 x^{5}}}\)
Рішення:
а.
\(\dfrac{\sqrt{72 x^{3}}}{\sqrt{162 x}}\)
Перепишіть, використовуючи властивість коефіцієнта,
\(\sqrt{\dfrac{72 x^{3}}{162 x}}\)
Видаліть загальні фактори.
\(\sqrt{\dfrac{\cancel{18} \cdot 4 \cdot x^{2} \cdot \cancel{x}}{\cancel{18} \cdot 9 \cdot \cancel{x}}}\)
Спростити.
\(\sqrt{\dfrac{4 x^{2}}{9}}\)
Спростити радикал.
\(\dfrac{2 x}{3}\)
б.
\(\dfrac{\sqrt[3]{32 x^{2}}}{\sqrt[3]{4 x^{5}}}\)
Перепишіть, використовуючи властивість коефіцієнта,\(\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\dfrac{a}{b}}\).
\(\sqrt[3]{\dfrac{32 x^{2}}{4 x^{5}}}\)
Спростити дріб під радикалом.
\(\sqrt[3]{\dfrac{8}{x^{3}}}\)
Спростити радикал.
\(\dfrac{2}{x}\)
Спростити:
- \(\dfrac{\sqrt{50 s^{3}}}{\sqrt{128 s}}\)
- \(\dfrac{\sqrt[3]{56 a}}{\sqrt[3]{7 a^{4}}}\)
- Відповідь
-
- \(\dfrac{5s}{8}\)
- \(\dfrac{2}{a}\)
Спростити:
- \(\dfrac{\sqrt{75 q^{5}}}{\sqrt{108 q}}\)
- \(\dfrac{\sqrt[3]{72 b^{2}}}{\sqrt[3]{9 b^{5}}}\)
- Відповідь
-
- \(\dfrac{5 q^{2}}{6}\)
- \(\dfrac{2}{b}\)
Спростити:
- \(\dfrac{\sqrt{147 a b^{8}}}{\sqrt{3 a^{3} b^{4}}}\)
- \(\dfrac{\sqrt[3]{-250 m n^{-2}}}{\sqrt[3]{2 m^{-2} n^{4}}}\)
Рішення:
а.
\(\dfrac{\sqrt{147 a b^{8}}}{\sqrt{3 a^{3} b^{4}}}\)
Перепишіть, використовуючи властивість коефіцієнта.
\(\sqrt{\dfrac{147 a b^{8}}{3 a^{3} b^{4}}}\)
Видаліть загальні фактори у фракції.
\(\sqrt{\dfrac{49 b^{4}}{a^{2}}}\)
Спростити радикал.
\(\dfrac{7 b^{2}}{a}\)
б.
\(\dfrac{\sqrt[3]{-250 m n^{-2}}}{\sqrt[3]{2 m^{-2} n^{4}}}\)
Перепишіть, використовуючи властивість коефіцієнта.
\(\sqrt[3]{\dfrac{-250 m n^{-2}}{2 m^{-2} n^{4}}}\)
Спростити дріб під радикалом.
\(\sqrt[3]{\dfrac{-125 m^{3}}{n^{6}}}\)
Спростити радикал.
\(-\dfrac{5 m}{n^{2}}\)
Спростити:
- \(\dfrac{\sqrt{162 x^{10} y^{2}}}{\sqrt{2 x^{6} y^{6}}}\)
- \(\dfrac{\sqrt[3]{-128 x^{2} y^{-1}}}{\sqrt[3]{2 x^{-1} y^{2}}}\)
- Відповідь
-
- \(\dfrac{9 x^{2}}{y^{2}}\)
- \(\dfrac{-4 x}{y}\)
Спростити:
- \(\dfrac{\sqrt{300 m^{3} n^{7}}}{\sqrt{3 m^{5} n}}\)
- \(\dfrac{\sqrt[3]{-81 p q^{-1}}}{\sqrt[3]{3 p^{-2} q^{5}}}\)
- Відповідь
-
- \(\dfrac{10 n^{3}}{m}\)
- \(\dfrac{-3 p}{q^{2}}\)
Спростити:\(\dfrac{\sqrt{54 x^{5} y^{3}}}{\sqrt{3 x^{2} y}}\)
Рішення:
\(\dfrac{\sqrt{54 x^{5} y^{3}}}{\sqrt{3 x^{2} y}}\)
Перепишіть, використовуючи властивість коефіцієнта.
\(\sqrt{\dfrac{54 x^{5} y^{3}}{3 x^{2} y}}\)
Видаліть загальні фактори у фракції.
\(\sqrt{18 x^{3} y^{2}}\)
Перепишіть радиканд як продукт, використовуючи найбільший ідеальний квадратний коефіцієнт.
\(\sqrt{9 x^{2} y^{2} \cdot 2 x}\)
Перепишіть радикал як добуток двох радикалів.
\(\sqrt{9 x^{2} y^{2}} \cdot \sqrt{2 x}\)
Спростити.
\(3 x y \sqrt{2 x}\)
Спростити:\(\dfrac{\sqrt{64 x^{4} y^{5}}}{\sqrt{2 x y^{3}}}\)
- Відповідь
-
\(4 x y \sqrt{2 x}\)
Спростити:\(\dfrac{\sqrt{96 a^{5} b^{4}}}{\sqrt{2 a^{3} b}}\)
- Відповідь
-
\(4 a b \sqrt{3 b}\)
Раціоналізувати знаменник з одним терміном
До того, як калькулятор став інструментом побуту, наближення значення дробу з радикалом в знаменнику було дуже громіздким процесом!
З цієї причини був розроблений процес, який отримав назву раціоналізація знаменника. Дріб з радикалом в знаменнику перетворюється в еквівалентний дріб, знаменником якого є ціле число. Квадратні корені чисел, які не є ідеальними квадратами, є ірраціональними числами. Коли ми раціоналізуємо знаменник, пишемо еквівалентний дріб з раціональним числом в знаменнику. Цей процес використовується і сьогодні, і корисний і в інших областях математики, теж.
Визначення\(\PageIndex{2}\): Rationalizing the Denominator
Раціоналізація знаменника - це процес перетворення дробу з радикалом в знаменнику в еквівалентний дріб, знаменником якого є ціле число.
Незважаючи на те, що у нас є калькулятори, доступні майже скрізь, фракція з радикалом у знаменнику все одно повинна бути раціоналізована. Не вважається спрощеним, якщо знаменник містить радикал.
Аналогічно радикальний вираз не вважається спрощеним, якщо радикаі містить дріб.
Спрощені радикальні вирази
Радикальний вираз вважається спрощеним, якщо є
- відсутні фактори в радикані мають досконалі сили індексу
- немає дробів в радиканді
- відсутність радикалів у знаменнику дробу
Щоб раціоналізувати знаменник з квадратним коренем, використовуємо властивість that\((\sqrt{a})^{2}=a\). Якщо скласти квадрат ірраціонального квадратного кореня, то отримаємо раціональне число.
Ми будемо використовувати цю властивість для раціоналізації знаменника в наступному прикладі.
Спростити:
- \(\dfrac{4}{\sqrt{3}}\)
- \(\sqrt{\dfrac{3}{20}}\)
- \(\dfrac{3}{\sqrt{6 x}}\)
Рішення:
Щоб раціоналізувати знаменник одним терміном, ми можемо помножити квадратний корінь на себе. Щоб зберегти еквівалент дробу, множимо і чисельник, і знаменник на один і той же коефіцієнт.
а.
|
|
|
| Помножте чисельник і знаменник на\(\sqrt{3}\). |
|
| Спростити. |
|
б. ми завжди спочатку спрощуємо радикал у знаменнику, перш ніж раціоналізувати його. Таким чином, цифри залишаються меншими і з ними легше працювати.
|
|
|
| Дріб не є ідеальним квадратом, тому перепишіть, використовуючи властивість частки. |
|
| Спростити знаменник. |
|
| Помножте чисельник і знаменник на\(\sqrt{5}\). |
|
| Спростити. |
|
| Спростити. |
|
c.
|
|
|
| Помножте чисельник і знаменник на\(\sqrt{6x}\). |
|
| Спростити. |
|
| Спростити. |
|
Спростити:
- \(\dfrac{5}{\sqrt{3}}\)
- \(\sqrt{\dfrac{3}{32}}\)
- \(\dfrac{2}{\sqrt{2 x}}\)
- Відповідь
-
- \(\dfrac{5 \sqrt{3}}{3}\)
- \(\dfrac{\sqrt{6}}{8}\)
- \(\dfrac{\sqrt{2 x}}{x}\)
Спростити:
- \(\dfrac{6}{\sqrt{5}}\)
- \(\sqrt{\dfrac{7}{18}}\)
- \(\dfrac{5}{\sqrt{5 x}}\)
- Відповідь
-
- \(\dfrac{6 \sqrt{5}}{5}\)
- \(\dfrac{\sqrt{14}}{6}\)
- \(\dfrac{\sqrt{5 x}}{x}\)
Коли ми раціоналізували квадратний корінь, ми помножили чисельник і знаменник на квадратний корінь, який дасть нам ідеальний квадрат під радикалом в знаменнику. Коли ми брали квадратний корінь, знаменник більше не мав радикалу.
Ми будемо стежити за аналогічним процесом, щоб раціоналізувати вищі корені. Щоб раціоналізувати знаменник з більш високим радикалом індексу, ми множимо чисельник і знаменник на радикал, який би дав нам радикал, і це ідеальна сила індексу. Коли ми спростимо новий радикал, знаменник більше не матиме радикалу.
Наприклад,
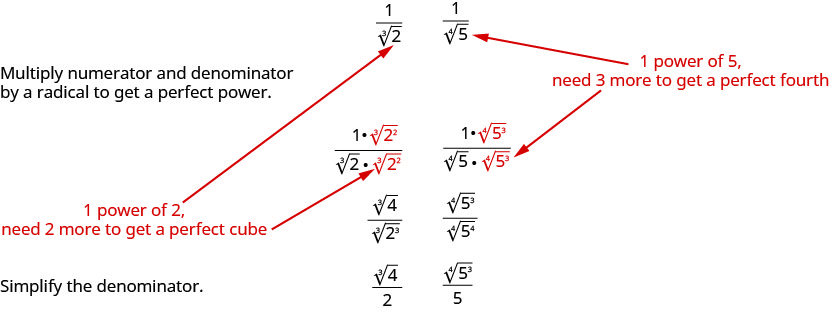
Цю техніку ми будемо використовувати в наступних прикладах.
Спростити:
- \(\dfrac{1}{\sqrt[3]{6}}\)
- \(\sqrt[3]{\dfrac{7}{24}}\)
- \(\dfrac{3}{\sqrt[3]{4 x}}\)
Рішення:
Щоб раціоналізувати знаменник з кубовим коренем, ми можемо помножити на кубовий корінь, який дасть нам ідеальний куб у радикані в знаменнику. Щоб зберегти еквівалент дробу, множимо і чисельник, і знаменник на один і той же коефіцієнт.
а.
|
|
|
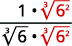
| Радикал в знаменнику має один коефіцієнт\(6\). Помножте і чисельник, і знаменник на\(\sqrt[3]{6^{2}}\), що дає нам\(2\) більше факторів\(6\). |
|
| Помножити. Зверніть увагу на радиканд в знаменнику має\(3\) повноваження\(6\). |
|
| Спростити корінь куба в знаменнику. |
|
б. ми завжди спочатку спрощуємо радикал у знаменнику, перш ніж раціоналізувати його. Таким чином, цифри залишаються меншими і з ними легше працювати.
|
|
|
| Дріб не є ідеальним кубом, тому перепишіть, використовуючи властивість Quotient. |
|
| Спростити знаменник. |
|
| Помножте чисельник і знаменник на\(\sqrt[3]{3^{2}}\). Це дасть нам\(3\) фактори\(3\). |
|
| Спростити. |
|
| Пам'ятайте,\(\sqrt[3]{3^{3}}=3\). |
|
| Спростити. |
|
c.
|
|
|
| Перепишіть радиканд, щоб показати фактори. |
|
| Помножте чисельник і знаменник на\(\sqrt[3]{2 \cdot x^{2}}\). Це дасть нам\(3\) фактори\(2\) і\(3\) фактори\(x\). |
|
| Спростити. |
|
| Спростити радикал в знаменнику. |
|
Спростити:
- \(\dfrac{1}{\sqrt[3]{7}}\)
- \(\sqrt[3]{\dfrac{5}{12}}\)
- \(\dfrac{5}{\sqrt[3]{9 y}}\)
- Відповідь
-
- \(\dfrac{\sqrt[3]{49}}{7}\)
- \(\dfrac{\sqrt[3]{90}}{6}\)
- \(\dfrac{5 \sqrt[3]{3 y^{2}}}{3 y}\)
Спростити:
- \(\dfrac{1}{\sqrt[3]{2}}\)
- \(\sqrt[3]{\dfrac{3}{20}}\)
- \(\dfrac{2}{\sqrt[3]{25 n}}\)
- Відповідь
-
- \(\dfrac{\sqrt[3]{4}}{2}\)
- \(\dfrac{\sqrt[3]{150}}{10}\)
- \(\dfrac{2 \sqrt[3]{5 n^{2}}}{5 n}\)
Спростити:
- \(\dfrac{1}{\sqrt[4]{2}}\)
- \(\sqrt[4]{\dfrac{5}{64}}\)
- \(\dfrac{2}{\sqrt[4]{8 x}}\)
Рішення:
Щоб раціоналізувати знаменник з четвертим коренем, ми можемо помножити на четвертий корінь, який дасть нам ідеальну четверту владу в радикані в знаменнику. Щоб зберегти еквівалент дробу, множимо і чисельник, і знаменник на один і той же коефіцієнт.
а.
|
|
|
| Радикал в знаменнику має один коефіцієнт\(2\). Помножте і чисельник, і знаменник на\(\sqrt[4]{2^{3}}\), що дає нам\(3\) більше факторів\(2\). |
|
| Помножити. Зверніть увагу на радиканд в знаменнику має\(4\) повноваження\(2\). |
|
| Спростити четвертий корінь в знаменнику. |
|
б. ми завжди спочатку спрощуємо радикал у знаменнику, перш ніж раціоналізувати його. Таким чином, цифри залишаються меншими і з ними легше працювати.
|
|
|
| Дріб не є ідеальною четвертою силою, тому перепишіть за допомогою Quotient Property. |
|
| Перепишіть радиканд в знаменник, щоб показати фактори. |
|
| Спростити знаменник. |
|
| Помножте чисельник і знаменник на\(\sqrt[4]{2^{2}}\). Це дасть нам\(4\) фактори\(2\). |
|
| Спростити. |
|
| Пам'ятайте,\(\sqrt[4]{2^{4}}=2\). |
|
| Спростити. |
|
c.
|
|
|
| Перепишіть радиканд, щоб показати фактори. |
|
| Помножте чисельник і знаменник на\(\sqrt[4]{2 \cdot x^{3}}\). Це дасть нам\(4\) фактори\(2\) і\(4\) фактори\(x\). |
|
| Спростити. |
|
| Спростити радикал в знаменнику. |
|
| Спростити дріб. |
|
Спростити:
- \(\dfrac{1}{\sqrt[4]{3}}\)
- \(\sqrt[4]{\dfrac{3}{64}}\)
- \(\dfrac{3}{\sqrt[4]{125 x}}\)
- Відповідь
-
- \(\dfrac{\sqrt[4]{27}}{3}\)
- \(\dfrac{\sqrt[4]{12}}{4}\)
- \(\dfrac{3 \sqrt[4]{5 x^{3}}}{5 x}\)
Спростити:
- \(\dfrac{1}{\sqrt[4]{5}}\)
- \(\sqrt[4]{\dfrac{7}{128}}\)
- \(\dfrac{4}{\sqrt[4]{4 x}}\)
- Відповідь
-
- \(\dfrac{\sqrt[4]{125}}{5}\)
- \(\dfrac{\sqrt[4]{224}}{8}\)
- \(\dfrac{\sqrt[4]{64 x^{3}}}{x}\)
Раціоналізувати двочленний знаменник
Коли знаменником дробу є сума або різниця з квадратними коренями, для раціоналізації знаменника ми використовуємо шаблон «Твір сполучених».
\(\begin{array}{c c}{(a-b)(a+b)} & {(2-\sqrt{5})(2+\sqrt{5})} \\ {a^{2}-b^{2}} &{ 2^{2}-(\sqrt{5})^{2}} \\ {}&{4-5} \\ {}&{-1}\end{array}\)
Коли ми множимо біном, який включає квадратний корінь за його сполученим, продукт не має квадратних коренів.
Спростити:\(\dfrac{5}{2-\sqrt{3}}\)
Рішення:
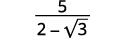 |
|
| Помножте чисельник і знаменник на сполучений знаменник. | 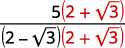 |
| Помножте відмінювання в знаменнику. | 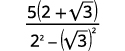 |
| Спростити знаменник. | 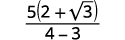 |
| Спростити знаменник. | 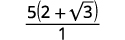 |
| Спростити. | 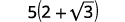 |
Спростити:\(\dfrac{3}{1-\sqrt{5}}\).
- Відповідь
-
\(-\dfrac{3(1+\sqrt{5})}{4}\)
Спростити:\(\dfrac{2}{4-\sqrt{6}}\).
- Відповідь
-
\(\dfrac{4+\sqrt{6}}{5}\)
Зверніть увагу, що ми не поширювали\(5\) у відповіді останнього прикладу. Залишивши результат фактованим, ми можемо побачити, чи є якісь фактори, які можуть бути загальними як для чисельника, так і для знаменника.
Спростити:\(\dfrac{\sqrt{3}}{\sqrt{u}-\sqrt{6}}\).
Рішення:
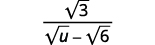 |
|
| Помножте чисельник і знаменник на сполучений знаменник. | 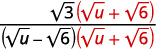 |
| Помножте відмінювання в знаменнику. | 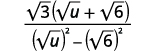 |
| Спростити знаменник. | 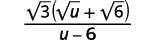 |
Спростити:\(\dfrac{\sqrt{5}}{\sqrt{x}+\sqrt{2}}\).
- Відповідь
-
\(\dfrac{\sqrt{5}(\sqrt{x}-\sqrt{2})}{x-2}\)
Спростити:\(\dfrac{\sqrt{10}}{\sqrt{y}-\sqrt{3}}\)
- Відповідь
-
\(\dfrac{\sqrt{10}(\sqrt{y}+\sqrt{3})}{y-3}\)
Будьте уважні до знаків при множенні. Чисельник і знаменник виглядають дуже схожими при множенні на сполучений.
Спростити:\(\dfrac{\sqrt{x}+\sqrt{7}}{\sqrt{x}-\sqrt{7}}\).
Рішення:
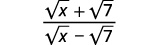 |
|
| Помножте чисельник і знаменник на сполучений знаменник. |  |
| Помножте відмінювання в знаменнику. | 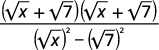 |
| Спростити знаменник. | 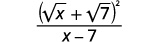 |
Ми не ставимо в квадрат чисельник. Залишивши його в факторованому вигляді, ми можемо побачити, що немає загальних факторів, які слід видалити з чисельника та знаменника.
Спростити:\(\dfrac{\sqrt{p}+\sqrt{2}}{\sqrt{p}-\sqrt{2}}\).
- Відповідь
-
\(\dfrac{(\sqrt{p}+\sqrt{2})^{2}}{p-2}\)
Спростити:\(\dfrac{\sqrt{q}-\sqrt{10}}{\sqrt{q}+\sqrt{10}}\)
- Відповідь
-
\(\dfrac{(\sqrt{q}-\sqrt{10})^{2}}{q-10}\)
Ключові концепції
- Коефіцієнтна властивість радикальних виразів
- Якщо\(\sqrt[n]{a}\) і\(\sqrt[n]{b}\) є дійсними числами\(b≠0\), а для будь-якого цілого числа\(n≥2\) то,\(\sqrt[n]{\dfrac{a}{b}}=\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}\) і\(\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\dfrac{a}{b}}\)
- Спрощені радикальні вирази
- Радикальний вираз вважається спрощеним, якщо є:
- відсутні фактори в радикані, які мають ідеальні сили індексу
- немає дробів в радиканді
- відсутність радикалів у знаменнику дробу
- Радикальний вираз вважається спрощеним, якщо є:
Глосарій
- раціоналізація знаменника
- Раціоналізація знаменника - це процес перетворення дробу з радикалом в знаменнику в еквівалентний дріб, знаменником якого є ціле число.