Глава 1 Огляд вправи

Розділ Огляд Вправи

Використання мови алгебри

Визначте множники та коефіцієнти

1. Використовуйте тести на подільність, щоб визначити, чи ділиться 180 на 2, на 3, на 5, на 6 та на 10.

Відповідь

Ділиться на$2,3,5,6$

2. Знайдіть просте факторизацію 252.

3. Знайдіть найменш поширене кратне 24 і 40.

Відповідь

120

У наступних вправах спрощуйте кожен вираз.

4. $24÷3+4(5−2)$

5. $7+3[6−4(5−4)]−3^2$

Відповідь

4

Оцінити вираз

У наступних вправах оцініть наступні вирази.

6. Коли$x=4$, ⓐ $x^3$ ⓑ $5x$ ⓒ $2x^2−5x+3$

7. $2x^2−4xy−3y^2$коли$x=3$ і$y=1$

Відповідь

3

Спростіть вирази, поєднуючи подібні терміни

У наступних вправах спростіть наступні вирази, комбінуючи подібні терміни.

8. $12y+7+2y−5$

9. $14x^2−9x+11−8x^2+8x−6$

Відповідь

$6x^2−x+5$

Перекласти англійську фразу на алгебраїчний вираз

У наступних вправах переводите фрази в алгебраїчні вирази.

10. ⓐ сума$4ab^2$$7a3b24ab^2$ і$7a^3b^2$

ⓑ продукт$6y^2$ і$3y$

ⓒ дванадцять більше$5x$

ⓓ$5y$ менше$8y^2$

11. ⓐ одинадцять разів різниця$y$ і два

ⓑ різниця в одинадцять разів$y$ і два

Відповідь

ⓐ$11(y−2)$
ⓑ$11y−2$

12. У Душка в кишені нікельси і копійки. Кількість копійок на чотири менше п'яти числа нікелів. Нехай nn представляє кількість нікелів. Напишіть вираз на кількість копійок.

Цілі числа

Спрощення виразів за допомогою абсолютного значення

У наступній вправі заповніть$<,>,$ або$=$ для кожної з наступних пар чисел.

13. ⓐ$−|7| \_\_\_−|−7|$

ⓑ$−8 \_\_\_−|−8|$

ⓒ$|−13| \_\_\_−13$

ⓓ$|−12| \_\_\_−(−12)$

Відповідь

ⓐ$=$
ⓑ$=$
ⓒ$>$
ⓓ$=$

У наступних вправах спростити.

14. $9−|3(4−8)|$

15. $12−3|1−4(4−2)|$

Відповідь

$−9$

Додавання та віднімання цілих чисел

У наступних вправах спрощуйте кожен вираз.

16. $−12+(−8)+7$

17. ⓐ$15−7$

ⓑ$−15−(−7)$

ⓒ$−15−7$

ⓓ$15−(−7)$

Відповідь

ⓐ$8$
ⓑ$−8$
ⓒ$−22$
ⓓ$22$

18. $−11−(−12)+5$

19. ⓐ$23−(−17)$ ⓑ$23+17$

Відповідь

ⓐ 40 ⓑ 40

20. $−(7−11)−(3−5)$

Множення та ділення цілих чисел

У наступній вправі множимо або ділимо.

21. ⓐ$−27÷9$ ⓑ$120÷(−8)$ ⓒ$4(−14)$ ⓓ$−1(−17)$

Відповідь

ⓐ$−3$ ⓑ$−15$ ⓒ$−56$ ⓓ$17$

Спрощення та оцінка виразів за допомогою цілих чисел

У наступних вправах спрощуйте кожен вираз.

22. ⓐ$(−7)^3$ ⓑ$−7^3$

23. $(7−11)(6−13)$

Відповідь

16

24. $63÷(−9)+(−36)÷(−4)$

25. $6−3|4(1−2)−(7−5)|$

Відповідь

$−12$

26. $(−2)^4−24÷(13−5)$

Для наступних вправ оцініть кожен вираз.

27. $(y+z)^2$коли$y=−4$ і$z=7$

Відповідь

9

28. $3x^2−2xy+4y^2$коли$x=−2$ і$y=−3$

Перекласти англійські фрази на алгебраїчні вирази

У наступних вправах переведіть на алгебраїчний вираз і спростіть, якщо це можливо.

29. сума$−4$ і$−9$, збільшена на$23$

Відповідь

$(−4+(−9))+23;10$

30. ⓐ різниця 17 і −8 ⓑ відняти 17 з −25

Використання цілих чисел у програмах

У наступній вправі вирішуйте.

31. Температура 10 липня висока температура у Фініксі, штат Арізона, становила 109°, а висока температура в Джуно, штат Аляска, була 63°. Яка різниця між температурою в Палм-Спрінгз і температурою в Уайтфілді?

Відповідь

$46°$

Дроби

Спрощення дробів

У наступних вправах спростити.

32. $\dfrac{204}{228}$

33. $−\dfrac{270x^3}{198y^2}$

Відповідь

$−\dfrac{15x^3}{11y^2}$

Множення та ділення дробів

У наступних вправах виконайте зазначену операцію.

34. $\left(−\dfrac{14}{15}\right)\left(\dfrac{10}{21}\right)$

35. $\dfrac{6x}{25}÷\dfrac{9y}{20}$

Відповідь

$\dfrac{8x}{15y}$

36. $\dfrac{−\frac{4}{9}}{\dfrac{8}{21}}$

Додавання та віднімання дробів

У наступних вправах виконайте зазначену операцію.

37. $\dfrac{5}{18}+\dfrac{7}{12}$

Відповідь

$\dfrac{31}{36}$

38. $\dfrac{11}{36}−\dfrac{15}{48}$

39. ⓐ$\dfrac{5}{8}+\dfrac{3}{4}$ ⓑ$\dfrac{5}{8}÷\dfrac{3}{4}$

Відповідь

ⓐ$\dfrac{11}{8}$ ⓑ$\dfrac{5}{6}$

40. ⓐ$−\dfrac{3y}{10}−\dfrac{5}{6}$ ⓑ$−\dfrac{3y}{10}·\dfrac{5}{6}$

Використовуйте порядок операцій для спрощення дробів

У наступних вправах спростити.

41. $\dfrac{4·3−2·5}{−6·3+2·3}$

Відповідь

$−\dfrac{1}{6}$

42. $\dfrac{4(7−3)−2(4−9)}{−3(4+2)+7(3−6)}$

43. $\dfrac{4^3−4^2}{(\dfrac{4}{5})^2}$

Відповідь

75

Обчислення змінних виразів за допомогою дробів

У наступних вправах оцініть.

44. $4x^2y^2$коли$x=\dfrac{2}{3}$ і$y=−\dfrac{3}{4}$

45. $\dfrac{a+b}{a−b}$коли$a=−4$ і$b=6$

Відповідь

$−15$

Десяткові

Круглі десяткові

46. $6.738$Округлити до найближчого ⓐ сотого ⓑ десятого ⓒ цілого числа.

Додавання та віднімання десяткових знаків

У наступних вправах виконайте зазначену операцію.

47. $−23.67+29.84$

Відповідь

$6.17$

48. $54.3−100$

49. $79.38−(−17.598)$

Відповідь

$96.978$

Множення та ділення десяткових знаків

У наступних вправах виконайте зазначену операцію.

50. $(−2.8)(3.97)$

51. $(−8.43)(−57.91)$

Відповідь

488.1813

52. $(53.48)(10)$

53. $(0.563)(100)$

Відповідь

$56.3$

54. $\$ 118.35÷2.6$

55. $1.84÷(−0.8)$

Відповідь

$−23$

Перетворення десяткових дробів, дробів і відсотків

У наступних вправах запишіть кожну десяткову дробу як дріб.

56. $\dfrac{13}{20}$

57. $−\dfrac{240}{25}$

Відповідь

$−9.6$

У наступних вправах перетворіть кожен дріб в десятковий.

58. $−\dfrac{5}{8}$

59. $\dfrac{14}{11}$

Відповідь

$1.\overline{27}$

У наступних вправах перетворіть кожне десяткове число в відсоток.

60. $2.43$

61. $0.0475$

Відповідь

$4.75 \%$

Спрощення виразів за допомогою квадратних коренів

У наступних вправах спростити.

62. $\sqrt{289}$

63. $\sqrt{−121}$

Відповідь

немає дійсного числа

Визначення цілих чисел, раціональних чисел, ірраціональних чисел та дійсних чисел

У наступній вправі перерахуйте ⓐ цілі числа ⓑ цілі числа ⓒ раціональні числа ⓓ ірраціональні числа ⓔ дійсні числа для кожного набору чисел

64. $−8,0,1.95286...,\dfrac{12}{5},\sqrt{36},9$

Знайдіть дроби та десяткові дроби на числовому рядку

У наступних вправах знайдіть цифри на числовому рядку.

65. $\dfrac{3}{4},−\dfrac{3}{4},1\dfrac{1}{3},−1\dfrac{2}{3},\dfrac{7}{2},−\dfrac{5}{2}$

Відповідь

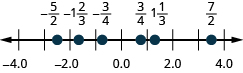
66. ⓐ$3.2$ ⓑ$−1.35$

Властивості дійсних чисел

Використання комутативних та асоціативних властивостей

У наступних вправах спростити.

67. $\dfrac{5}{8}x+\dfrac{5}{12}y+\dfrac{1}{8}x+\dfrac{7}{12}y$

Відповідь

$\dfrac{3}{4}x+y$

68. $−32·9·\dfrac{5}{8}$

69. $\left(\dfrac{11}{15}+\dfrac{3}{8}\right)+\dfrac{5}{8}$

Відповідь

$1\dfrac{11}{15}$

Використання властивостей ідентичності, зворотного та нульового

У наступних вправах спростити.

70. $\dfrac{4}{7}+\dfrac{8}{15}+\left(−\dfrac{4}{7}\right)$

71. $\dfrac{13}{15}·\dfrac{9}{17}·\dfrac{15}{13}$

Відповідь

$\dfrac{9}{17}$

72. $\dfrac{0}{x−3},x\neq 3$

73. $\dfrac{5x−7}{0},5x−7\neq 0$

Відповідь

невизначений

Спрощення виразів за допомогою властивості розподілу

У наступних вправах спростіть використання розподільної властивості.

74. $8(a−4)$

75. $12\left(\dfrac{2}{3}b+\dfrac{5}{6}\right)$

Відповідь

$8b+10$

76. $18·\dfrac{5}{6}(2x−5)$

77. $(x−5)p$

Відповідь

$xp−5p$

78. $−4(y−3)$

79. $12−6(x+3)$

Відповідь

$−6x−6$

80. $6(3x−4)−(−5)$

81. $5(2y+3)−(4y−1)$

Відповідь

$y+16$

Практичний тест

1. Знайдіть просте факторизацію$756$.

2. Поєднуйте подібні терміни:$5n+8+2n−1$

Відповідь

$7n+7$

3. Оцініть, коли$x=−2$ і$y=3: \dfrac{|3x−4y|}{6}$

4. Переведіть на алгебраїчний вираз і спростіть:

ⓐ одинадцять менше, ніж негативні вісім

ⓑ різниця$−8$ і$−3$, збільшена на 5

Відповідь

$−8−11 = −19$
$(−8−(−3))+5 = 0$

5. У Душка в кишені нікельси і копійки. Кількість копійок в сім менше, ніж в чотири рази перевищує кількість нікелів. Нехай nn представляє кількість нікелів. Напишіть вираз на кількість копійок.

6. $28.1458$Округлити до найближчого

ⓐ сотий ⓑ тисячний

Відповідь

ⓐ$28.15$ ⓑ$28.146$

7. Перетворити

ⓐ$\dfrac{5}{11}$ до десяткового ⓑ$1.15$ до відсотка

8. Знайдіть$\dfrac{3}{5},2.8,and−\dfrac{5}{2}$ на числовому рядку.

Відповідь

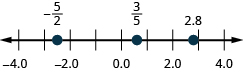
У наступних вправах спрощуйте кожен вираз.

9. $8+3[6−3(5−2)]−4^2$

10. $−(4−9)−(9−5)$

Відповідь

1

11. $56÷(−8)+(−27)÷(−3)$

12. $16−2|3(1−4)−(8−5)|$

Відповідь

$−8$

13. $−5+2(−3)^2−9$

14. $\dfrac{180}{204}$

Відповідь

$\dfrac{15}{17}$

15. $−\dfrac{7}{18}+\dfrac{5}{12}$

16. $\dfrac{4}{5}÷(−\dfrac{12}{25})$

Відповідь

$−\dfrac{5}{3}$

17. $\dfrac{9−3·9}{15−9}$

18. $\dfrac{4(−3+2(3−6))}{3(11−3(2+3))}$

Відповідь

$3$

19. $\dfrac{5}{13}⋅\dfrac{4}{7}⋅\dfrac{13}{5}$

20. $\dfrac{−\dfrac{5}{9}}{\dfrac{10}{21}}$

Відповідь

$−\dfrac{7}{6}$

21. $−4.8+(−6.7)$

22. $34.6−100$

Відповідь

$−65.4$

23. $−12.04⋅(4.2)$

24. $−8÷0.05$

Відповідь

160

25. $−\sqrt{121}$

26. $(\dfrac{8}{13}+\dfrac{5}{7})+\dfrac{2}{7}$

Відповідь

$1\dfrac{8}{13}$

27. $5x+(−8y)−6x+3y$

28. ⓐ$\dfrac{0}{9}$ ⓑ$\dfrac{11}{0}$

Відповідь

ⓐ 0 ⓑ невизначений

29. $−3(8x−5)$

30. $6(3y−1)−(5y−3)$

Відповідь

$13y−3$