Skip to main content
LibreTexts - Ukrayinska

1.6E: Вправи

  1. Last updated
  2. Save as PDF
  • Page ID
    59593

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Практика робить досконалим

    Використання комутативних та асоціативних властивостей

    У наступних вправах спростити.

    1. \(43m+(−12n)+(−16m)+(−9n)\)

    Відповідь

    \(27m+(−21n)\)

    2. \(−22p+17q+(−35p)+(−27q)\)

    3. \(\frac{3}{8}g+\frac{1}{12}h+\frac{7}{8}g+\frac{5}{12}h\)

    Відповідь

    \(\frac{5}{4}g+\frac{1}{2}h\)

    4. \(\frac{5}{6}a+\frac{3}{10}b+\frac{1}{6}a+\frac{9}{10}b\)

    5. \(6.8p+9.14q+(−4.37p)+(−0.88q)\)

    Відповідь

    \(2.43p+8.26q\)

    6. \(9.6m+7.22n+(−2.19m)+(−0.65n)\)

    7. \(−24·7·\frac{3}{8}\)

    Відповідь

    \(−63\)

    8. \(−36·11·\frac{4}{9}\)

    9. \(\left(\frac{5}{6}+\frac{8}{15}\right)+\frac{7}{15}\)

    Відповідь

    \(1\frac{5}{6}\)

    10. \(\left(\frac{11}{12}+\frac{4}{9}\right)+\frac{5}{9}\)

    11. \(17(0.25)(4)\)

    Відповідь

    \(17\)

    12. \(36(0.2)(5)\)

    13. \([2.48(12)](0.5)\)

    Відповідь

    \(14.88\)

    14. \([9.731(4)](0.75)\)

    15. \(12\left(\frac{5}{6}p\right)\)

    Відповідь

    \(10p\)

    16. \(20\left(\frac{3}{5}q\right)\)

    Використання властивостей ідентичності, зворотного та нульового

    У наступних вправах спростити.

    17. \(19a+44−19a\)

    Відповідь

    \(44\)

    18. \(27c+16−27c\)

    19. \(\frac{1}{2}+\frac{7}{8}+\left(−\frac{1}{2}\right)\)

    Відповідь

    \(\frac{7}{8}\)

    20. \(\frac{2}{5}+\frac{5}{12}+\left(−\frac{2}{5}\right)\)

    21. \(10(0.1d)\)

    Відповідь

    \(d\)

    22. \(100(0.01p)\)

    23. \(\frac{3}{20}·\frac{49}{11}·\frac{20}{3}\)

    Відповідь

    \(\frac{49}{11}\)

    24. \(\frac{13}{18}·\frac{25}{7}·\frac{18}{13}\)

    25. \(\frac{0}{u−4.99}\), де\(u\neq 4.99\)

    Відповідь

    \(0\)

    26. \(0÷(y−\frac{1}{6})\), де\(x \neq 16\)

    27. \(\frac{32−5a}{0}\), де\(32−5a\neq 0\)

    Відповідь

    невизначений

    28. \(\frac{28−9b}{0}\), де\(28−9b\neq 0\)

    29. \(\left(\frac{3}{4}+\frac{9}{10}m\right)÷0\), де\(\frac{3}{4}+\frac{9}{10}m\neq 0\)

    Відповідь

    невизначений

    30. \(\left(\frac{5}{16}n−\frac{3}{7}\right)÷0\), де\(\frac{5}{16}n−\frac{3}{7}\neq 0\)

    Спрощення виразів за допомогою властивості розподілу

    У наступних вправах спростіть використання розподільної властивості.

    31. \(8(4y+9)\)

    Відповідь

    \(32y+72\)

    32. \(9(3w+7)\)

    33. \(6(c−13)\)

    Відповідь

    \(6c−78\)

    34. \(7(y−13)\)

    35. \(\frac{1}{4}(3q+12)\)

    Відповідь

    \(\frac{3}{4}q+3\)

    36. \(\frac{1}{5}(4m+20)\)

    37. \(9(\frac{5}{9}y−\frac{1}{3})\)

    Відповідь

    \(5y−3\)

    38. \(10(\frac{3}{10}x−\frac{2}{5})\)

    39. \(12(\frac{1}{4}+\frac{2}{3}r)\)

    Відповідь

    \(3+8r\)

    40. \(12(\frac{1}{6}+\frac{3}{4}s)\)

    41. \(15⋅\frac{3}{5}(4d+10)\)

    Відповідь

    \(36d+90\)

    42. \(18⋅\frac{5}{6}(15h+24)\)

    43. \(r(s−18)\)

    Відповідь

    \(rs−18r\)

    44. \(u(v−10)\)

    45. \((y+4)p\)

    Відповідь

    \(yp+4p\)

    46. \((a+7)x\)

    47. \(−7(4p+1)\)

    Відповідь

    \(−28p−7\)

    48. \(−9(9a+4)\)

    49. \(−3(x−6)\)

    Відповідь

    \(−3x+18\)

    50. \(−4(q−7)\)

    51. \(−(3x−7)\)

    Відповідь

    \(−3x+7\)

    52. \(−(5p−4)\)

    53. \(16−3(y+8)\)

    Відповідь

    \(−3y−8\)

    54. \(18−4(x+2)\)

    55. \(4−11(3c−2)\)

    Відповідь

    \(−33c+26\)

    56. \(9−6(7n−5)\)

    57. \(22−(a+3)\)

    Відповідь

    \(−a+19\)

    58. \(8−(r−7)\)

    59. \((5m−3)−(m+7)\)

    Відповідь

    \(4m−10\)

    60. \((4y−1)−(y−2)\)

    61. \(9(8x−3)−(−2)\)

    Відповідь

    \(72x−25\)

    62. \(4(6x−1)−(−8)\)

    63. \(5(2n+9)+12(n−3)\)

    Відповідь

    \(22n+9\)

    64. \(9(5u+8)+2(u−6)\)

    65. \(14(c−1)−8(c−6)\)

    Відповідь

    \(6c+34\)

    66. \(11(n−7)−5(n−1)\)

    67. \(6(7y+8)−(30y−15)\)

    Відповідь

    \(12y+63\)

    68. \(7(3n+9)−(4n−13)\)

    Письмові вправи

    69. Своїми словами, викласти асоціативну властивість додавання.

    Відповідь

    Відповіді будуть відрізнятися.

    70. У чому різниця між адитивним оберненим і мультиплікативним оберненим числа

    71. Спростіть\(8(x−\frac{1}{4})\) використання розподільної властивості та поясніть кожен крок.

    Відповідь

    Відповіді будуть відрізнятися.

    72. Поясніть, як можна розмножувати\(4($5.97)\) без паперу чи калькулятора, думаючи про те\($5.97\), як,\(6−0.03\) а потім використовуючи розподільну властивість.

    Самостійна перевірка

    а Після виконання вправ використовуйте цей контрольний список, щоб оцінити своє володіння цілями цього розділу.

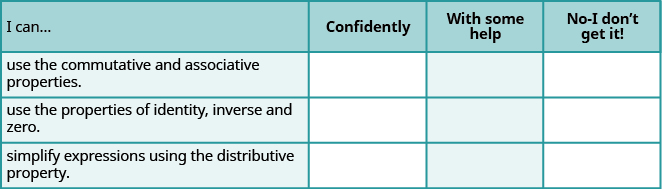
    Ця таблиця має 4 стовпці, 3 рядки та рядок заголовка. Рядок заголовка позначає кожен стовпець я можу, впевнено, з деякою допомогою і ні, я не розумію. Перший стовпець має такі твердження: використовувати комутативні та асоціативні властивості, використовувати властивості ідентичності, зворотного і нульового, спростити вирази за допомогою Distributive Property. Решта стовпці порожні.

    б Ознайомившись з цим контрольним списком, що ви будете робити, щоб стати впевненими у всіх цілях?