1.2: Використовуйте мову алгебри
- Page ID
- 59585
До кінця цього розділу ви зможете:
- Знайти множники, прості множники та найменш поширені кратні
- Використання змінних та алгебраїчних символів
- Спрощення виразів за допомогою порядку операцій
- Оцінити вираз
- Визначте та комбінуйте подібні терміни
- Перекласти англійську фразу на алгебраїчний вираз
Цей розділ покликаний бути коротким оглядом понять, які знадобляться в курсі проміжної алгебри. Більш ретельне ознайомлення з темами, висвітленими в цьому розділі, можна знайти в розділі Елементарна алгебра, Основи.
Пошук факторів, простих факторизацій та найменш поширених кратних
Числа 2, 4, 6, 8, 10, 12 називаються кратними 2. Кратне 2 може бути записано як добуток рахункового числа і 2.
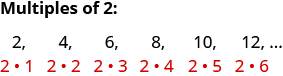
Аналогічно, кратне 3 буде добутком числа підрахунку і 3.

Ми могли б знайти кратні будь-якому числу, продовжуючи цей процес.
| Кількість підрахунку | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Кратні 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| Кратні 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| Кратні 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 |
| Кратні 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| Кратні 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 |
| Кратні 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 |
| Кратні 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 |
| Кратні 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 |
Число кратне,\(n\) якщо воно є добутком лічильного числа і\(n\).
Інший спосіб сказати, що 15 кратний 3 - це сказати, що 15 ділиться на 3. Це означає, що коли ми ділимо 3 на 15, ми отримуємо лічильне число. Насправді,\(15÷3\) є\(5\), так і\(15\) є\(5⋅3\).
Якщо число\(m\) кратне\(n\), то\(m\) ділиться на\(n\).
Якби ми шукали закономірності в кратних чисел від 2 до 9, ми виявили б такі тести на подільність:
Число ділиться на:
- 2, якщо остання цифра дорівнює 0, 2, 4, 6 або 8.
- 3, якщо сума цифр ділиться на 3.
- 5, якщо остання цифра дорівнює 5 або 0.
- 6, якщо він ділиться як на 2, так і на 3.
- 10, якщо він закінчується на 0.
5 625 ділиться на
- 2?
- 3?
- 5 або 10?
- 6?
- Відповідь
-
а.
\(\text{Is 5,625 divisible by 2?}\)
\( \begin{array}{ll} \text{Does it end in 0, 2, 4, 6 or 8?} & {\text{No.} \\ \text{5,625 is not divisible by 2.}} \end{array}\) - б.
\(\text{5,625 divisible by 3?}\)
\(\begin{array}{ll} {\text{What is the sum of the digits?} \\ \text{Is the sum divisible by 3?}} & {5+6+2+5=18 \\ \text{Yes.} \\ \text{5,625 is divisible by 3.}}\end{array}\) - c.
\(\text{Is 5,625 divisible by 5 or 10?}\)
\(\begin{array}{ll} \text{What is the last digit? It is 5.} & \text{5,625 is divisible by 5 but not by 10.} \end{array}\)д.\(\text{Is 5,625 divisible by 6?}\)
\(\begin{array}{ll}\text{Is it divisible by both 2 and 3?} & {\text{No, 5,625 is not divisible by 2, so 5,625 is} \\ \text{not divisible by 6.}} \end{array}\)
Чи 4,962 ділиться на 2? б. 3? c. 5? д. 6? е. 10?
- Відповідь
-
a. так б. да c. ні d. да e. ні
Чи є 3,765 ділиться на 2? б. 3? c. 5? д. 6? е. 10?
- Відповідь
-
а. ні б. да c. да d. ні e. ні
У математиці часто існує кілька способів говорити про одні й ті ж ідеї. Поки що ми бачили, що якщо\(m\) є кратним\(n\), ми можемо сказати,\(m\) що ділиться на\(n\). Наприклад, оскільки 72 кратна 8, ми говоримо, що 72 ділиться на 8. Оскільки 72 кратна 9, ми говоримо, що 72 ділиться на 9. Ми можемо висловити це ще іншим способом.
Так як\(8·9=72\), ми говоримо, що 8 і 9 - фактори 72. Коли ми пишемо\(72=8·9\), ми говоримо, що ми враховували 72.
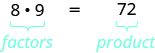
Іншими способами фактора\(72\) є\(1·72, \; 2·36, \; 3·24, \; 4·18,\) і\(6⋅12\). Число 72 має безліч факторів:\(1,\,2,\,3,\,4,\,6,\,8,\,9,\,12,\,18,\,24,\,36,\) і\(72\).
Якщо\(a\) і\(b\) йдуть підрахунок чисел, а\(a·b=m\), то\(a\) і\(b\) є факторами\(m\).
Деякі цифри, такі як 72, мають багато факторів. Інші числа мають лише два фактори. Просте число - це лічильне число більше 1, єдиними факторами якого є 1 і саме по собі.
Просте число - це лічильне число більше 1, єдиними факторами якого є 1 і саме число.
Складене число - це лічильне число, яке не є простим. Складене число має множники, відмінні від 1, і саме число.
Числа підрахунку від 2 до 20 наведені в таблиці з їх коефіцієнтами. Обов'язково погоджуйтеся з «основним» або «складовим» етикеткою для кожного!
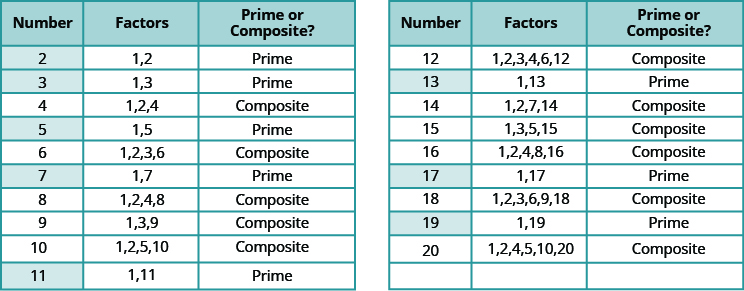
Простими числами менше 20 є 2, 3, 5, 7, 11, 13, 17 і 19. Зверніть увагу, що єдине парне просте число - 2.
Складене число можна записати як унікальний твір простих чисел. Це називається простим факторизацією числа. Пошук простого факторизації складеного числа буде корисним у багатьох темах цього курсу.
Просте факторизація числа - це добуток простих чисел, що дорівнює числу.
Щоб знайти просте факторизацію складеного числа, знайдіть будь-які два множники числа і використовуйте їх для створення двох гілок. Якщо коефіцієнт є простим, ця гілка завершена. Коло, що просте. В іншому випадку легко втратити сліди простих чисел.
Якщо коефіцієнт не простий, знайдіть два множника числа і продовжуйте процес. Після того, як всі гілки обвели прості числа в кінці, факторизація завершена. Складене число тепер можна записати як добуток простих чисел.
Фактор 48.
- Відповідь
-


.jpg)
Ми говоримо\(2⋅2⋅2⋅2⋅3\), що це основна факторизація 48. Ми зазвичай пишемо прості числа в порядку зростання. Обов'язково помножте коефіцієнти, щоб перевірити свою відповідь. \(2⋅2⋅2⋅2⋅3\)є основним факторизацією 48. Ми зазвичай пишемо прості числа в порядку зростання. Обов'язково помножте коефіцієнти, щоб перевірити свою відповідь.
Якби ми спочатку враховували 48 по-іншому, наприклад, як\(6·8\), результат все одно був би таким же. Закінчіть основну факторизацію і переконайтеся в цьому самі.
Знайдіть просте факторизацію\(80\).
- Відповідь
-
\(2⋅2⋅2⋅2⋅5\)
Знайдіть просте факторизацію\(60\).
- Відповідь
-
\(2⋅2⋅3⋅5\)
- Знайдіть два фактори, твором яких є задане число, і використовуйте ці числа для створення двох гілок.
- Якщо коефіцієнт є простим, ця гілка завершена. Обведіть прайм, як листочок на дереві.
- Якщо коефіцієнт не є простим, запишіть його як добуток двох факторів і продовжуйте процес.
- Запишіть складене число як добуток всіх обведених простих чисел.
Однією з причин, чому ми розглядаємо прості числа, є використання цих методів, щоб знайти найменш поширене кратне двом числам. Це буде корисно, коли ми додаємо і віднімаємо дроби з різними знаменниками.
Найменш поширене кратне (НСМ) двох чисел - це найменше число, кратне обом числам.
Щоб знайти найменш поширене кратне двох чисел, ми будемо використовувати метод простих факторів. Давайте знайдемо LCM 12 і 18, використовуючи їх прості множники.
Знайдіть найменш поширене кратне (НКМ) 12 і 18 за допомогою методу простих факторів.
- Відповідь
-

.jpg)


Зверніть увагу, що прості множники 12\((2·2·3)\) і прості\((2⋅3⋅3)\) множники 18 включені в НКМ\((2·2·3·3)\). Таким чином, 36 є найменш поширеним кратним 12 і 18.
При зіставленні загальних простих чисел кожен загальний простий коефіцієнт використовується лише один раз. Таким чином ви впевнені, що 36 є найменш поширеним кратним.
Знайдіть LCM 9 та 12 за допомогою методу простих факторів.
- Відповідь
-
36
Знайдіть LCM 18 і 24 за допомогою методу простих факторів.
- Відповідь
-
72
- Запишіть кожне число як добуток простих чисел.
- Перерахуйте простих чисел кожного числа. Зіставте прості числа вертикально, коли це можливо.
- Збиваємо колони.
- Помножте коефіцієнти.
Використовувати змінні та алгебраїчні символи
В алгебрі ми використовуємо букву алфавіту для представлення числа, значення якого може змінитися. Ми називаємо це змінною і літери, які зазвичай використовуються для змінних є\(x,\,y,\,a,\,b,\) і\(c.\)
Змінна - це буква, яка представляє число, значення якого може змінюватися.
Число, значення якого завжди залишається незмінним, називається константою.
Константа - це число, значення якого завжди залишається однаковим.
Щоб писати алгебраїчно, нам потрібні деякі символи операції, а також числа та змінні. Є кілька типів символів, які ми будемо використовувати. Існує чотири основні арифметичні операції: додавання, віднімання, множення та ділення. Нижче ми перерахуємо символи, які використовуються для позначення цих операцій.
| Операція | Позначення | Скажіть: | Результат - це... |
|---|---|---|---|
| Додавання | \(a+b\) | \(a\)плюс\(b\) | сума\(a\) і\(b\) |
| Віднімання | \(a−b\) | \(a\)мінус\(b\) | різниця\(a\) і\(b\) |
| множення | \(a⋅b,\,ab,\,(a)(b),\,(a)b,\,a(b)\) | \(a\)раз\(b\) | продукт\(a\) і\(b\) |
| Відділ | \(a÷b,\,\space a/b,\,\space\frac{a}{b},\,\space b \overline{\smash{)}a}\) | \(a\)розділений на\(b\) | частка\(a\) і\(b\); \(a\) називається дивідендом, і\(b\) називається дільником |
Коли дві величини мають однакове значення, ми говоримо, що вони рівні і з'єднуємо їх знаком рівності.
\(a=b\)\(a\)читається "дорівнює»\(b\).
Символ «\(=\)» називається знаком рівності.
На числовому рядку числа стають більшими, коли вони йдуть зліва направо. Цифровий рядок може використовуватися для пояснення символів «\(<\)» і «\(>\)».

Вирази\(a<b\) або\(a>b\) можуть бути прочитані зліва направо або справа наліво, хоча англійською мовою ми зазвичай читаємо зліва направо. Загалом,
\[a<b \text{ is equivalent to }b>a. \text{For example, } 7<11 \text{ is equivalent to }11>7.\]
\[a>b \text{ is equivalent to }b<a. \text{For example, } 17>4 \text{ is equivalent to }4<17.\]
| Символи нерівності | Слова |
|---|---|
| \(a\neq b\) | \(a\)не дорівнює\(b\). |
| \(a<b\) | \(a\)менше, ніж\(b\). |
| \(a\leq b\) | \(a\)менше або дорівнює\(b\). |
| \(a>b\) | \(a\)більше, ніж\(b\). |
| \(a\geq b\) | \(a\)більше або дорівнює\(b\). |
Угруповання символів в алгебрі багато в чому схожі на коми, двокрапки та інші розділові знаки в англійській мові. Вони допомагають ідентифікувати вираз, який може бути складений з числа, змінної або комбінації чисел і змінних за допомогою символів операції. Зараз ми представимо три типи символів групування.
\[\begin{array}{lc} \text{Parentheses} & \mathrm{()} \\ \text{Brackets} & \mathrm{[]} \\ \text{Braces} & \mathrm{ \{ \} } \end{array}\]
Ось кілька прикладів виразів, які містять символи групування. Ми спростимо такі вирази пізніше в цьому розділі.
\[8(14−8) \qquad 21−3[2+4(9−8)] \qquad 24÷ \{13−2[1(6−5)+4]\}\]
Яка різниця в англійській мові між фразою і реченням? Фраза виражає єдину думку, яка сама по собі неповна, але речення робить повне твердження. У реченні є підмет і дієслово. В алгебрі ми маємо вирази і рівняння.
Вираз - це число, змінна або комбінація чисел і змінних з використанням символів операції.
\[\begin{array}{lll} \textbf{Expression} & \textbf{Words} & \textbf{English Phrase} \\ \mathrm{3+5} & \text{3 plus 5} & \text{the sum of three and five} \\ \mathrm{n−1} & n\text{ minus one} & \text{the difference of } n \text{ and one} \\ \mathrm{6·7} & \text{6 times 7} & \text{the product of six and seven} \\ \frac{x}{y} & x \text{ divided by }y & \text{the quotient of }x \text{ and }y \end{array} \]
Зверніть увагу, що англійські фрази не утворюють повного речення, оскільки фраза не має дієслова.
Рівняння - це два вирази, пов'язані знаком рівності. Коли ви читаєте слова, які символи представляють у рівнянні, у вас є повне речення англійською мовою. Знак рівності дає дієслово.
Рівняння - це два вирази, з'єднані знаком рівності.
\[\begin{array}{ll} \textbf{Equation} & \textbf{English Sentence} \\ 3+5=8 & \text{The sum of three and five is equal to eight.} \\ n−1=14 & n \text{ minus one equals fourteen.} \\ 6·7=42 & \text{The product of six and seven is equal to forty-two.} \\ x=53 & x \text{ is equal to fifty-three.} \\ y+9=2y−3 & y \text{ plus nine is equal to two } y \text{ minus three.} \end{array}\]
Припустимо, нам потрібно помножити 2 дев'ять разів. Ми могли б написати це як\(2·2·2·2·2·2·2·2·2\). Це нудно, і це може бути важко відстежувати всі ці 2s, тому ми використовуємо експоненти. Пишемо\(2·2·2\) як\(\mathrm{2^3}\) і\(2·2·2·2·2·2·2·2·2\) як\(2^9\). У таких виразах\(2^3\), як, 2 називається основою, а 3 називається експонентою. Показник підказує нам, скільки разів нам потрібно помножити базу.

Ми говоримо\(2^3\), що знаходиться в експоненціальному позначенні і\(2·2·2\) знаходиться в розширеному позначенні.
\(a^n\)означає\(n\) множинні коефіцієнти числа\(a\).
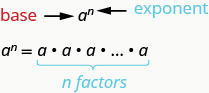
Вираз\(a^n\)\(a\) читається\(n^{th}\) владі.
Поки ми читаємо про\(a^n\)\(“a\)\(n^{th}\) владу», ми зазвичай читаємо:
\[\begin{array}{cc} a^2 & “a \text{ squared}” \\ a^3 & “a \text{ cubed}” \end{array}\]
Пізніше ми побачимо, чому\(a^2\) і\(a^3\) мають спеціальні імена.
Таблиця показує, як ми читаємо деякі вирази з показниками.
| Вираз | У словах | |
|---|---|---|
| 7 2 | 7 до другої потужності або | 7 в квадраті |
| 5 3 | 5 до третьої потужності або | 5 кубічних |
| 9 4 | 9 до четвертої потужності | |
| 12 5 | 12 до п'ятої влади |
Спрощення виразів за допомогою порядку операцій
Спростити вираз означає зробити всі математичні можливості. Наприклад, для спрощення\(\mathrm{4·2+1}\) ми спочатку помножимо,\(\mathrm{4⋅2}\) щоб отримати 8, а потім додати 1, щоб отримати 9. Хороша звичка для розвитку - опрацювати сторінку, записуючи кожен крок процесу нижче попереднього кроку. Щойно описаний приклад виглядатиме наступним чином:
\[ 4⋅2+1 \\ 8+1 \\ 9\]
Не використовуючи знак рівності при спрощенні виразу, ви можете уникнути плутанини виразів з рівняннями.
Щоб спростити вираз, виконайте всі операції у виразі.
Ми ввели більшість символів і позначень, що використовуються в алгебрі, але тепер нам потрібно уточнити порядок операцій. В іншому випадку вирази можуть мати різне значення, і вони можуть привести до різних значень.
Наприклад, розглянемо вираз\(4+3⋅7\). Деякі студенти спрощують це отримання 49, шляхом додавання,\(4+3\) а потім множення цього результату на 7. Інші отримують 25, множивши\(3·7\) спочатку, а потім додаючи 4.
Один і той же вираз має дати той же результат. Так математики встановили деякі орієнтири, які називаються порядком операцій.
- Дужки та інші символи групування
- Спростіть усі вирази всередині дужок або інших символів групування, спочатку працюючи над самими внутрішніми дужками.
- Експоненти
- Спростити всі вирази з показниками.
- Множення і ділення
- Виконайте все множення і ділення по порядку зліва направо. Ці операції мають однаковий пріоритет.
- Додавання і віднімання
- Виконайте всі додавання і віднімання по порядку зліва направо. Ці операції мають однаковий пріоритет.
Студенти часто запитують: «Як я запам'ятаю наказ?» Ось спосіб допомогти вам запам'ятати: Візьміть першу букву кожного ключового слова і підмініть дурну фразу «Будь ласка, вибачте, моя дорога тітка Саллі».
\[\begin{array}{ll} \text{Parentheses} & \text{Please} \\ \text{Exponents} & \text{Excuse} \\ \text{Multiplication Division} & \text{My Dear} \\ \text{Addition Subtraction} & \text{Aunt Sally} \end{array}\]
Добре, що «M y D ear» йде разом, оскільки це нагадує нам, що моє множення та поділ D мають однаковий пріоритет. Ми не завжди робимо множення перед діленням або завжди робимо ділення перед множенням. Робимо їх по порядку зліва направо.
Аналогічно, «Союз одиниці S» йде разом і так нагадує нам, що додавання та віднімання також мають однаковий пріоритет, і ми робимо їх у порядку зліва направо.
Спростити:\(18÷6+4(5−2)\).
- Відповідь
-
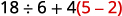
Дужки? Так, спочатку відніміть. 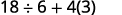
Експоненти? Ні. Множення або ділення? Так. Ділимо спочатку, тому що множимо і ділимо зліва направо. 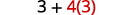
Будь-яке інше множення або ділення? Так. Помножити. 
Будь-яке інше множення ділення? Ні. Будь-яке додавання або віднімання? Так. Додати. 
Спростити:\(30÷5+10(3−2).\)
- Відповідь
-
16
Спростити:\(70÷10+4(6−2).\)
- Відповідь
-
23
Коли є кілька символів групування, ми спочатку спрощуємо внутрішні дужки і працюємо назовні.
Спростити:\(5+2^3+3[6−3(4−2)].\)
- Відповідь
-
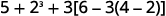
Чи є круглі дужки (або інші символи групування)? Так. 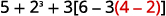
Зосередьтеся на дужках, які знаходяться всередині дужок. Відніміть. 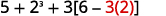
Продовжуйте всередині дужок і множте. 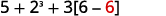
Продовжуйте всередині дужок і відніміть. 
Вираз всередині дужок не вимагає подальшого спрощення. Чи є якісь експоненти? Так. Спрощення експонентів. 
Чи є множення або ділення? Так. Помножити. 
Чи є додавання віднімання? Так. Додати. 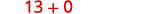
Додати. 
Спростити:\(9+5^3−[4(9+3)].\)
- Відповідь
-
86
Спростити:\(7^2−2[4(5+1)].\)
- Відповідь
-
1
Оцінити вираз
В останніх кількох прикладах ми спростили вирази, використовуючи порядок операцій. Тепер ми оцінимо деякі вирази - знову слідуючи порядку операцій. Оцінити вираз означає знайти значення виразу при заміні змінної на задане число.
Оцінити вираз означає знайти значення виразу при заміні змінної на задане число.
Щоб оцінити вираз, підставити це число для змінної у виразі, а потім спростити вираз.
Оцініть, коли\(x=4\): а.\(x^2\) б.\(3^x\) с\(2x^2+3x+8\).
- Відповідь
-
а.
б.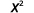
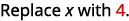

Використовуйте визначення показника. 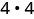
Спростити. 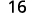
c.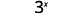
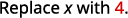

Використовуйте визначення показника. 
Спростити. 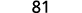
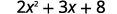
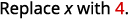
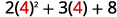
Слідкуйте за порядком операцій. .jpg)
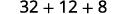
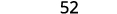
Оцініть\(x=3\), коли, а.\(x^2\) б.\(4^x\) с\(3x^2+4x+1\).
- Відповідь
-
а. 9
б. 64
с. 40
Оцініть\(x=6\), коли, а.\(x^3\) б.\(2^x\) с\(6x^2−4x−7\).
- Відповідь
-
а. 216
б. 64
с. 185
Визначте та комбінуйте подібні терміни
Алгебраїчні вирази складаються з термінів. Термін - це константа, або добуток константи і однієї або декількох змінних.
Термін - це константа або добуток константи і однієї або декількох змінних.
Прикладами термінів є\(7,\,y,\,5x^2,\,9a,\) і\(b^5\).
Константа, яка множить змінну, називається коефіцієнтом.
Коефіцієнт члена - це константа, яка множить змінну в термін.
Подумайте про коефіцієнт як число перед змінною. Коефіцієнт терміну\(3x\) дорівнює 3. Коли ми пишемо\(x\), коефіцієнт дорівнює 1, так як\(x=1⋅x\).
Деякі терміни мають спільні риси. Коли два члени є константами або мають однакову змінну та експоненту, ми говоримо, що вони схожі на терміни.
Подивіться на наступні 6 термінів. Які з них, здається, мають спільні риси?
\[5x \quad 7 \quad n^2 \quad 4 \quad 3x \quad 9n^2\]
Ми кажемо,
\(7\)і\(4\) схожі на терміни.
\(5x\)і\(3x\) схожі на терміни.
\(n^2\)і\(9n^2\) схожі на терміни.
Терміни, які є або константами, або мають однакові змінні, підняті до одних і тих же повноважень, називаються як терміни.
Якщо в виразі є подібні терміни, ви можете спростити вираз, об'єднавши подібні терміни. Складаємо коефіцієнти і зберігаємо ту ж змінну.
\[\begin{array}{lc} \text{Simplify.} & 4x+7x+x \\ \text{Add the coefficients.} & 12x \end{array}\]
Спростити:\(2x^2+3x+7+x^2+4x+5\).
- Відповідь
-



Спростити:\(3x^2+7x+9+7x^2+9x+8\).
- Відповідь
-
\(10x^2+16x+17\)
Спростити:\(4y^2+5y+2+8y^2+4y+5.\)
- Відповідь
-
\(12y^2+9y+7\)
- Визначте подібні терміни.
- Перевпорядкуйте вираз так, як терміни разом.
- Додайте або відніміть коефіцієнти і зберігайте однакову змінну для кожної групи подібних термінів.
Перекласти англійську фразу на алгебраїчний вираз
Ми перерахували багато символів операцій, які використовуються в алгебрі. Тепер ми будемо використовувати їх для перекладу англійських фраз в алгебраїчні вирази. Символи та змінні, про які ми говорили, допоможуть нам це зробити. Таблиця їх підсумовує.
| Операція | Фраза | Вираз |
|---|---|---|
| Додавання | \(a\)плюс\(b\)
сума\(a\) і\(b\) \(a\)збільшився на\(b\) \(b\)більше\(a\) загальна кількість\(a\) і\(b\) \(b\)додано до\(a\) |
\(a+b\) |
| Віднімання | \(a\)мінус\(b\)
різниця\(a\) і\(b\) \(a\)зменшився на\(b\) \(b\)менше\(a\) \(b\)віднімається з\(a\) |
\(a−b\) |
| множення | \(a\)раз\(b\)
продукт\(a\) і\(b\) двічі\(a\) |
\(a·b,\,ab,\,a(b),\,(a)(b)\)
\(2a\) |
| Відділ | \(a\)розділений на\(b\)
частка\(a\) і\(b\) співвідношення\(a\) і\(b\) \(b\)розділений на\(a\) |
\(a÷b,\,a/b,\,\frac{a}{b},\,b \overline{\smash{)}a}\) |
Подивіться уважно на ці фрази, використовуючи чотири операції:

Кожна фраза говорить нам оперувати двома числами. Шукайте слова і і, щоб знайти цифри.
Кожна фраза говорить нам оперувати двома числами. Шукайте слова і і, щоб знайти цифри.
Переведіть кожну англійську фразу в алгебраїчний вираз:
a. різниця\(14x\) і\(9\)
b. частка\(8y^2\) і\(3\)c. дванадцять більше\(y\)
d. сім менше\(49x^2\)
- Відповідь
-
а Ключовим словом є різниця, яка говорить нам, що операція є віднімання. Шукайте слова і t o знайти числа для віднімання.
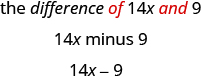
б Ключове слово - коефіцієнт, який говорить нам, що операція - це поділ.

c. ключових слів більше, ніж. Вони кажуть нам, що операція є доповненням. Більше, ніж означає «додано до».
\[\text{twelve more than }y \\ \text{twelve added to }y \\ y+12\]
d Ключові слова менше, ніж. Вони кажуть нам відняти. Менше, ніж означає «віднімається з».
\[\text{seven less than }49x^2 \\ \text{seven subtracted from }49x^2 \\ 49x^2−7\]
Перекладіть англійську фразу в алгебраїчний вираз:
a. різниця\(14x^2\) і\(13\)
b. частка\(12x\) і\(2\)
c.\(13\) більше\(z\)
d.\(18\) менше\(8x\)
- Відповідь
-
а.\(14x^2−13\) б.\(12x÷2\)
в.\(z+13\) д.\(8x−18\)
Перекладіть англійську фразу в алгебраїчний вираз:
a. сума\(17y^2\) і\(19\)
b. продукт\(7\) і\(y\)
c Одинадцять більше\(x\)
d. чотирнадцять менше\(11a\)
- Відповідь
-
а.\(17y^2+19\) б.\(7y\)
в.\(x+11\) д.\(11a−14\)
Ми уважно дивимося на слова, щоб допомогти нам розрізнити множення суми та додавання товару.
Перекладіть англійську фразу в алгебраїчний вираз:
a. у вісім разів перевищує суму\(x\) і\(y\)
b. сума у вісім разів\(x\) і\(y\)
- Відповідь
-
Є два операції words— раз говорить нам помножити і сума говорить нам, щоб додати.
а Оскільки ми\(8\) множимо на суму, нам потрібні дужки навколо суми\(x\) і\(y\),\((x+y)\). Це змушує спочатку визначити суму. (Запам'ятайте порядок операцій.)
\[\text{eight times the sum of }x \text{ and }y \\ 8(x+y)\]
б Щоб взяти суму, шукаємо слова і і щоб побачити, що додається. Тут беремо суму вісім разів\(x\) і\(y\).
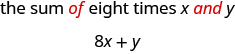
Перекладіть англійську фразу в алгебраїчний вираз:
a. чотири рази більше суми\(p\) і\(q\)
б. сума в чотири рази\(p\) і\(q\)
- Відповідь
-
а.\(4(p+q)\) б.\(4p+q\)
Перекладіть англійську фразу в алгебраїчний вираз:
a. різниця в два рази\(x\) і\(8\)
б. в два рази різниця\(x\) і\(8\)
- Відповідь
-
а.\(2x−8\) б.\(2(x−8)\)
Пізніше в цьому курсі ми будемо застосовувати наші навички алгебри для вирішення додатків. Першим кроком буде переклад англійської фрази на алгебраїчний вираз. Ми побачимо, як це зробити в наступних двох прикладах.
Довжина прямокутника на 14 менше ширини. \(w\)Дозволяти представляти ширину прямокутника. Напишіть вираз для довжини прямокутника.
- Відповідь
-
\[\begin{array}{lc} \text{Write a phrase about the length of the rectangle.} & \text{14 less than the width} \\ \text{Substitute }w \text{ for “the width.”} & w \\ \text{Rewrite less than as subtracted from.} & \text{14 subtracted from } w \\ \text{Translate the phrase into algebra.} & w−14 \end{array}\]
Довжина прямокутника на 7 менше ширини. \(w\)Дозволяти представляти ширину прямокутника. Напишіть вираз для довжини прямокутника.
- Відповідь
-
\(w−7\)
Ширина прямокутника\(6\) менше довжини. \(l\)Дозволяти представляти довжину прямокутника. Напишіть вираз для ширини прямокутника.
- Відповідь
-
\(l−6\)
Вирази в наступному прикладі будуть використані в типових задачах із сумішшю монет, які ми побачимо найближчим часом.
У Джун в сумочці є копійки і чверті. Кількість копійок в сім менше, ніж в чотири рази перевищує кількість чвертей. \(q\)Дозволяти представляти кількість чвертей. Напишіть вираз для кількості копійок.
- Відповідь
-
\[\begin{array}{lc} \text{Write a phrase about the number of dimes.} & \text{7 less than 4 times }q \\ \text{Translate 4 times }q. & \text{7 less than 4}q \\ \text{Translate the phrase into algebra.} & 4q−7 \end{array}\]
Джеффрі має копійки і чверті в кишені. Кількість копійок у вісім менше, ніж в чотири рази перевищує кількість чвертей. \(q\)Дозволяти представляти кількість чвертей. Напишіть вираз для кількості копійок.
- Відповідь
-
\(4q−8\)
Лорен має копійки і нікельси в сумочці. Кількість копійок в три більше семи разів перевищує кількість нікелів. \(n\)Дозволяти представляти кількість нікелів. Напишіть вираз для кількості копійок.
- Відповідь
-
\(7n+3\)
Ключові концепції
- Тести
на подільність Число ділиться на:
2, якщо остання цифра дорівнює 0, 2, 4, 6 або 8.
3, якщо сума цифр ділиться на 3.
5, якщо остання цифра дорівнює 5 або 0.
6, якщо він ділиться як на 2, так і на 3.
10, якщо він закінчується на 0. - Як знайти просту факторизацію складеного числа.
- Знайдіть два фактори, твором яких є задане число, і використовуйте ці числа для створення двох гілок.
- Якщо коефіцієнт є простим, ця гілка завершена. Обведіть прайм, як бутон на дереві.
- Якщо коефіцієнт не є простим, запишіть його як добуток двох факторів і продовжуйте процес.
- Запишіть складене число як добуток всіх обведених простих чисел.
- Як знайти найменш поширене кратне за допомогою методу простих факторів.
- Запишіть кожне число як добуток простих чисел.
- Перерахуйте простих чисел кожного числа. Зіставте прості числа вертикально, коли це можливо.
- Збиваємо колони.
- Помножте коефіцієнти.
- Символ рівності
\(a=b\)\(a\) читається «дорівнює»\(b\). Символ «=» називається знаком рівності. 
- Символи нерівності
Символи нерівності Слова \(a≠b\) \(a\)не дорівнює\(b\). \(a<b\) \(a\)менше, ніж\(b\). \(a≤b\) \(a\)менше або дорівнює\(b\). \(a>b\) \(a\)більше, ніж\(b\). \(a≥b\) \(a\)більше або дорівнює \(b\). - Угруповання символів\(\begin{array}{lc} \text{Parentheses} & \mathrm{()} \\ \text{Brackets} & \mathrm{[]} \\ \text{Braces} & \mathrm{ \{ \} } \end{array}\)
- Експоненціальне позначення\(a^n\) означає \(a\)помножити на себе, \(n\)раз. Вираз an \(a\)читається\(n^{th}\) владі.
- Спрощення виразу
Щоб спростити вираз, виконайте всі операції у виразі. - Як користуватися порядком операцій.
- Дужки та інші символи групування
- Спростіть усі вирази всередині дужок або інших символів групування, спочатку працюючи над самими внутрішніми дужками.
- Експоненти
- Спростити всі вирази з показниками.
- Множення і ділення
- Виконайте все множення і ділення по порядку зліва направо. Ці операції мають однаковий пріоритет.
- Додавання і віднімання
- Виконайте всі додавання і віднімання по порядку зліва направо. Ці операції мають однаковий пріоритет.
- Дужки та інші символи групування
- Як поєднувати подібні терміни.
- Визначте подібні терміни.
- Перевпорядкуйте вираз так, як терміни разом.
- Додайте або відніміть коефіцієнти і зберігайте однакову змінну для кожної групи подібних термінів.
Операція Фраза Вираз Додавання \(a\)плюс \(b\)
сума \(a\)і \(b\)
\(a\)збільшена \(b\)
\(b\)більш ніж на\(a\)
загальна сума \(a\)та \(b\)
\(b\)додана до\(a\)\(a+b\) Віднімання \(a\)мінус \(b\)
різниця\(a\) і \(b\)
\(a\)зменшилася на \(b\)
\(b\)менше\(a\)
\(b\)віднімається з\(a\)\(a−b\) множення \(a\)разів більше \(b\)
продукту \(a\)і в \(b\)
два рази\(a\)\(a·b,\,ab,\,a(b),\,(a)(b)\)
\(2a\)
Відділ \(a\)розділений на \(b\)
частка \(a\)і \(b\)
співвідношення \(a\)і \(b\)
\(b\)розділений на\(a\)\(a÷b,\,a/b,\,\frac{a}{b},\,b \overline{\smash{)}a}\)
Глосарій
- коефіцієнт
- Коефіцієнт члена - це константа, яка множить змінну в термін.
- складене число
- Складене число - це лічильне число, яке не є простим. Він має фактори, відмінні від 1, і саме число.
- постійна
- Константа - це число, значення якого завжди залишається однаковим.
- ділиться на число
- Якщо число \(m\)кратне \(n\), то \(m\)ділиться на \(n\).
- рівняння
- Рівняння - це два вирази, з'єднані знаком рівності.
- оцінювати вираз
- Оцінити вираз означає знайти значення виразу при заміні змінних заданим числом.
- вираз
- Вираз - це число, змінна або комбінація чисел і змінних з використанням символів операції.
- чинники
- Якщо\(a·b=m\), то \(a\)і \(b\)є чинниками \(m\).
- найменш поширене кратне
- Найменш поширене кратне (НСМ) двох чисел - це найменше число, кратне обом числам.
- як терміни
- Терміни, які є або константами, або мають однакові змінні, підняті до одних і тих же повноважень, називаються як терміни.
- кратне числу
- Число кратне, \(n\)якщо воно є добутком лічильного числа і \(n\).
- порядок операцій
- Порядок операцій встановлюються керівні принципи для спрощення виразу.
- основна факторизація
- Просте факторизація числа - це добуток простих чисел, що дорівнює числу.
- просте число
- Просте число - це лічильне число більше 1, єдиними факторами якого є 1 і саме число.
- спростити вираз
- Спростити вираз означає зробити всі математичні можливості.
- термін
- Термін - це константа, або добуток константи і однієї або декількох змінних.
- змінна
- Змінна - це буква, яка представляє число, значення якого може змінюватися.
