1.3: Цілі числа
- Page ID
- 59565
До кінця цього розділу ви зможете:
- Спрощення виразів з абсолютним значенням
- Додавання та віднімання цілих чисел
- Множення і ділення цілих чисел
- Спрощення виразів цілими числами
- Оцінити змінні вирази цілими числами
- Перекладіть фрази на вирази з цілими числами
- Використання цілих чисел у додатках
Більш ретельне ознайомлення з темами, висвітленими в цьому розділі, можна знайти в розділі Елементарна алгебра, Основи.
Спрощення виразів за допомогою абсолютного значення
Від'ємним числом є число менше 0. Від'ємні числа знаходяться зліва від нуля на числовому рядку (рис.\(\PageIndex{1}\)).
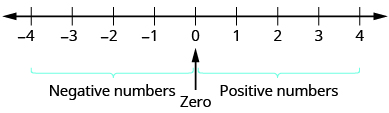
Малюнок\(\PageIndex{1}\). Числовий рядок показує розташування позитивних і від'ємних чисел.
Можливо, ви помітили, що на числовому рядку негативні числа є дзеркальним відображенням позитивних чисел, з нулем посередині. Оскільки числа\(2\) і\(−2\) знаходяться на однаковій відстані від нуля, кожне з них називається протилежним іншому. \(2\)Протилежне є\(−2\), а\(−2\) протилежне є\(2\).
Протилежність числу - це число, яке на тій же відстані від нуля на числовій лінії, але на протилежній стороні нуля.
Малюнок\(\PageIndex{2}\) ілюструє визначення.

Малюнок\(\PageIndex{2}\). Протилежність 3 є\(−3\).
\[\begin{align} & -a \text{ means the opposite of the number }a \\ & \text{The notation} -a \text{ is read as “the opposite of }a \text{.”} \end{align} \]
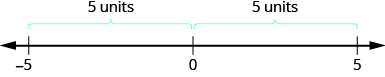
Ми побачили, що такі числа, як 3 і −3, протилежні, тому що вони однакові відстані від 0 на числовій лінії. Вони обидва три одиниці від 0. Відстань між 0 і будь-яким числом на числовому рядку називається абсолютним значенням цього числа.
Абсолютне значення числа - це його відстань від 0 на числовому рядку.
Абсолютне значення числа\(n\) записується як\(|n|\) і\(|n|≥0\) для всіх чисел.
Абсолютні значення завжди більше або рівні нулю.
Наприклад,
\[\begin{align} & -5 \text{ is } 5 \text{ units away from 0, so } |-5|=5. \\ & 5 \text{ is }5\text{ units away from 0, so }|5|=5. \end{align}\]
Малюнок\(\PageIndex{3}\) ілюструє цю ідею.
Абсолютне значення числа ніколи не є від'ємним, оскільки відстань не може бути від'ємною. Єдине число з абсолютним значенням, рівним нулю, - це саме число нуль, оскільки відстань від 0 до 0 на числовому рядку дорівнює нулю одиниць.
У наступному прикладі ми впорядкуємо вирази з абсолютними значеннями.
Заповніть\(<,\,>,\) або\(=\) для кожної з наступних пар чисел:
- \(\mathrm{|−5|}\_\_\mathrm{−|−5|}\_\_\mathrm{−|5|}\)
- \(\text{8__−|−8|}\)
- \(\text{−9__−|−9|}\)
- (\ текст {− (−16) __|−16|}\).
- Відповідь
-
а.
\(\begin{array}{lrcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {|−5| \\ 5 \\ 5 \\ |−5|} & {\_\_ \\ \_\_ \\ > \\ >} & {−|−5| \\ −5 \\ −5 \\ −|−5|} \end{array}\)
б.
\(\begin{array}{llcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {8 \\ 8 \\ 8 \\ 8} & {\_\_ \\ \_\_ \\ > \\ >} & {−|−8| \\ −8 \\ −8 \\ −|−8|} \end{array}\)
c.
\(\begin{array}{lrcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {−9 \\ −9 \\ −9 \\ −9} & {\_\_ \\ \_\_ \\ = \\ =} & {−|−9| \\ −9 \\ −9 \\ −|−9|} \end{array}\)
д.
\(\begin{array}{lrcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {−(−16) \\ 16 \\ 16 \\ −(−16)} & {\_\_ \\ \_\_ \\ = \\ =} & {−|−16| \\ 16 \\ 16 \\ |−16|} \end{array}\)
Заповніть\(<,\,>,\) або\(=\) для кожної з наступних пар чисел:
ⓐ\(−9 \_\_−|−9|\) ⓑ\(2 \_\_−|−2|\) ⓒ\(−8 \_\_|−8|\) ⓓ\(−(−9) \_\_|−9|.\)
- Відповідь
-
ⓐ\(>\) ⓑ\(>\) ⓒ\(<\)
ⓓ\(=\)
Заповніть\(<,>,\) або\(=\) для кожної з наступних пар чисел:
- \(7 \_\_ −|−7|\)
- \(−(−10) \_ \_|−10|\)
- \(|−4| \_\_ −|−4|\)
- \(−1 \_\_ |−1|.\)
- Відповідь
-
ⓐ\(>\) ⓑ\(=\) ⓒ\(>\)
ⓓ\(<\)
Тепер ми додаємо стовпчики абсолютних значень до нашого списку символів групування. Коли ми використовуємо порядок операцій, спочатку максимально спрощуємо всередині барів абсолютного значення, потім приймаємо абсолютне значення отриманого числа.
\[\begin{array}{lclc} \text{Parentheses} & () & \text{Braces} & \{ \} \\ \text{Brackets} & [] & \text{Absolute value} & ||\end{array}\]
У наступному прикладі ми спочатку спрощуємо вирази всередині барів абсолютних значень так само, як це робимо з дужками.
Спростити:\(\mathrm{24−|19−3(6−2)|}\).
- Відповідь
-
\(\begin{array}{lc} \text{} & 24−|19−3(6−2)| \\ \text{Work inside parentheses first:} & \text{} \\ \text{subtract 2 from 6.} & 24−|19−3(4)| \\ \text{Multiply 3(4).} & 24−|19−12| \\ \text{Subtract inside the absolute value bars.} & 24−|7| \\ \text{Take the absolute value.} & 24−7 \\ \text{Subtract.} & 17 \end{array}\)
Спростити:\(19−|11−4(3−1)|\).
- Відповідь
-
16
Спростити:\(9−|8−4(7−5)|\).
- Відповідь
-
9
Додавання та віднімання цілих чисел
Поки що в наших прикладах ми використовували лише підрахунок чисел і цілих чисел.
\[\begin{array}{ll} \text{Counting numbers} & 1,2,3… \\ \text{Whole numbers} 0,1,2,3…. \end{array}\]
Наша робота з протилежностями дає нам спосіб визначити цілі числа. Цілі числа і їх протилежності називаються цілими числами. Цілі числа - це числа\(…−3,−2,−1,0,1,2,3…\)
Цілі числа і їх протилежності називаються цілими числами.
Цілі числа - це числа
\[…-3,-2,-1,0,1,2,3…,\]
Більшість учнів влаштовують додавання і віднімання фактів для позитивних чисел. Але робити додавання або віднімання як з позитивними, так і з негативними числами може бути більш складним завданням.
Ми будемо використовувати два лічильники кольорів для моделювання додавання та віднімання негативів, щоб ви могли візуалізувати процедури замість запам'ятовування правил.
Ми дозволяємо одному кольору (синій) представляти позитив. Інший колір (червоний) буде представляти негативи.

Якщо у нас один позитивний лічильник і один негативний лічильник, значення пари дорівнює нулю. Вони утворюють нейтральну пару. Значення цієї нейтральної пари дорівнює нулю.
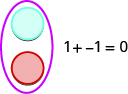
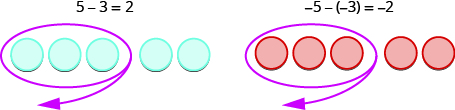
Ми будемо використовувати лічильники, щоб показати, як додати:
\[5+3 \; \; \; \; \; \; −5+(−3) \; \; \; \; \; \; −5+3 \; \; \; \; \; \; \; 5+(−3)\]
Перший приклад,\(5+3,\) додає 5 позитивів і 3 позитиви - обидва позитиви.
Другий приклад\(−5+(−3),\) додає 5 негативів і 3 негативів - обидва негативи.
Коли знаки однакові, лічильники все одного кольору, і тому ми їх додаємо. У кожному випадку ми отримуємо 8 - або 8 позитивів, або 8 негативів.

Так що ж відбувається, коли ознаки різні? Давайте додамо\(−5+3\) і\(5+(−3)\).
Коли ми використовуємо лічильники для моделювання додавання позитивних і негативних цілих чисел, легко побачити, чи є більше позитивних або більше негативних лічильників. Таким чином, ми знаємо, буде сума позитивною чи негативною.
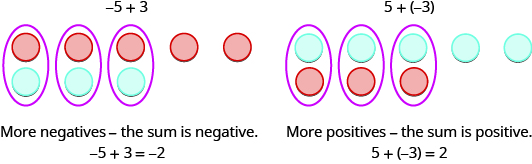
Додати: ⓐ\(−1+(−4)\) ⓑ\(−1+5\) ⓒ\(1+(−5)\).
- Відповідь
-
ⓐ
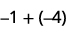

1 негативний плюс 4 негативи - це 5 негативів 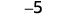
ⓑ
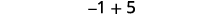

Позитивів більше, тому сума позитивна. 
ⓒ
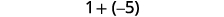

Негативів більше, тому сума негативна. 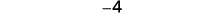
Додати: ⓐ\(−2+(−4)\) ⓑ\(−2+4\) ⓒ\(2+(−4)\).
- Відповідь
-
ⓐ\(−6\) ⓑ\(2\) ⓒ\(−2\)
Додати: ⓐ\(−2+(−5)\) ⓑ\(−2+5\) ⓒ\(2+(−5)\).
- Відповідь
-
ⓐ\(−7\) ⓑ\(3\) ⓒ\(−3\)
Ми продовжимо використовувати лічильники для моделювання віднімання. Можливо, коли ви були молодшими, ви читали\(“5−3”\) як «5 забрати 3». Коли ви використовуєте лічильники, ви можете думати про віднімання так само!
Ми будемо використовувати лічильники, щоб показати, щоб відняти:
\[5−3 \; \; \; \; \; \; −5−(−3) \; \; \; \; \; \; −5−3 \; \; \; \; \; \; 5−(−3) \]
У першому прикладі\(5−3\) ми віднімаємо 3 позитиви з 5 позитивів і в кінцевому підсумку з 2 позитивами.
У другому прикладі\(−5−(−3),\) ми віднімаємо 3 негативу з 5 негативів і в кінцевому підсумку з 2 негативами.
У кожному прикладі використовувалися лічильники тільки одного кольору, а «відняти» модель віднімання було легко застосувати.
Що відбувається, коли нам доводиться відняти одне позитивне і одне негативне число? Нам потрібно буде використовувати як сині, так і червоні лічильники, а також деякі нейтральні пари. Якщо у нас немає кількості лічильників, необхідних для забирання, ми додаємо нейтральні пари. Додавання нейтральної пари не змінює значення. Це як зміна кварталів на нікель-значення однакове, але виглядає інакше.
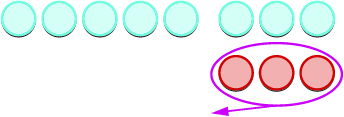
Давайте розглянемо\(−5−3\) і\(5−(−3)\).
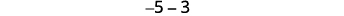 |
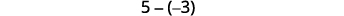 |
|
| Модель першого номера. |  |
 |
| Тепер додаємо потрібні нейтральні пари. |  |
 |
| Прибираємо кількість лічильників, змодельованих другим номером. | 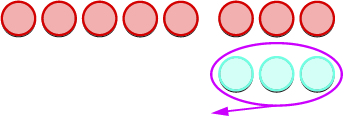 |
 |
| Порахуйте те, що залишилося. |  |
 |
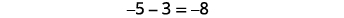 |
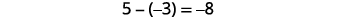 |
|
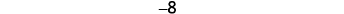 |
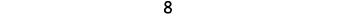 |
Відніміть: ⓐ\(3−1\) ⓑ\(−3−(−1)\) ⓒ\(−3−1\) ⓓ\(3−(−1)\).
- Відповідь
-
ⓐ
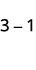
Візьміть 1 позитив з 3 позитивів і отримаєте 2 позитиви. 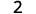
ⓑ

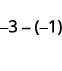
Візьміть 1 позитив з 3 негативів і отримаєте 2 негативу. 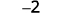
ⓒ

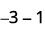
Візьміть 1 позитив з доданої нейтральної пари. 
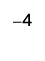
ⓓ

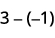
Візьміть 1 негатив з доданої нейтральної пари. 

Відніміть: ⓐ\(6−4\) ⓑ\(−6−(−4)\) ⓒ\(−6−4\) ⓓ\(6−(−4)\).
- Відповідь
-
ⓐ\(2\) ⓑ\(−2\) ⓒ\(−10\) ⓓ\(10\)
Відніміть: ⓐ\(7−4\) ⓑ\(−7−(−4)\) ⓒ\(−7−4\) ⓓ\(7−(−4)\).
- Відповідь
-
ⓐ\(3\) ⓑ\(−3\) ⓒ\(−11\) ⓓ\(11\)
Ви помітили, що віднімання знакових чисел можна зробити шляхом додавання протилежного? В останньому прикладі\(−3−1\) це те ж саме,\(3−(−1)\) що\(−3+(−1)\) і таке ж, як\(3+1\). Ви часто побачите цю ідею, властивість віднімання, написану наступним чином:
\[a−b=a+(−b)\]
Віднімання числа - це те саме, що і додавання його протилежності.
Спростити: ⓐ\(13−8\) і\(13+(−8)\) ⓑ\(−17−9\) і\(−17+(−9)\) ⓒ\(9−(−15)\) і\(9+15\) ⓓ\(−7−(−4)\) і\(−7+4\).
- Відповідь
-
ⓐ
\(\begin{array}{lccc} \text{} & 13−8 & \text{and} & 13+(−8) \\ \text{Subtract.} & 5 & \text{} & 5 \end{array}\)ⓑ
\(\begin{array}{lccc} \text{} & −17−9 & \text{and} & −17+(−9) \\ \text{Subtract.} & −26 & \text{} & −26 \end{array}\)
ⓒ
\(\begin{array}{lccc} \text{} & 9−(−15) & \text{and} & 9+15 \\ \text{Subtract.} & 24 & \text{} & 24 \end{array}\)
ⓓ
\(\begin{array}{lccc} \text{} & −7−(−4) & \text{and} & −7+4 \\ \text{Subtract.} & −3 & \text{} & −3 \end{array}\)
Спростити: ⓐ\(21−13\) і\(21+(−13)\) ⓑ\(−11−7\) і\(−11+(−7)\) ⓒ\(6−(−13)\) і\(6+13\) ⓓ\(−5−(−1)\) і\(−5+1\).
- Відповідь
-
ⓐ\(8,8\) ⓑ\(−18,−18\)
ⓒ\(19,19\) ⓓ\(−4,−4\)
Спростити: ⓐ\(15−7\) і\(15+(−7)\) ⓑ\(−14−8\) і\(−14+(−8)\) ⓒ\(4−(−19)\) і\(4+19\) ⓓ\(−4−(−7)\) і\(−4+7\).
- Відповідь
-
ⓐ\(8,8\) ⓑ\(−22,−22\)
ⓒ\(23,23\) ⓓ\(3,3\)
Що відбувається, коли є більше трьох цілих чисел? Ми просто використовуємо порядок операцій як зазвичай.
Спростити:\(7−(−4−3)−9.\)
- Відповідь
-
\(\begin{array}{lc} \text{} & 7−(−4−3)−9 \\ \text{Simplify inside the parentheses first.} & 7−(−7)−9 \\ \text{Subtract left to right.} & 14−9 \\ \text{Subtract.} & 5 \end{array}\)
Спростити:\(8−(−3−1)−9.\)
- Відповідь
-
3
Спростити:\(12−(−9−6)−14.\)
- Відповідь
-
13
Множення та ділення цілих чисел
Оскільки множення є математичним скороченням для повторного додавання, наша модель може бути легко застосована для показу множення цілих чисел. Давайте розглянемо цю конкретну модель, щоб побачити, які візерунки ми помічаємо. Ми будемо використовувати ті ж приклади, які ми використовували для додавання і віднімання. Тут ми використовуємо модель лише для того, щоб допомогти нам виявити візерунок.
Ми пам'ятаємо, що a⋅ba·b означає додати a, b раз.
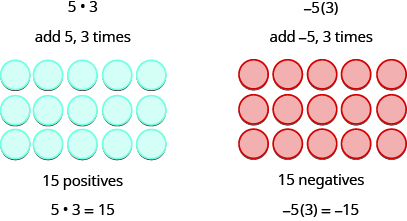
Наступні два приклади більш цікаві. Що означає помножити 5 на −3? Це означає відніміть 5,3 рази. Дивлячись на віднімання як на «віднімання», значить відняти 5, 3 рази. Але відняти нічого, тому починаємо з додавання нейтральних пар на робочу область.
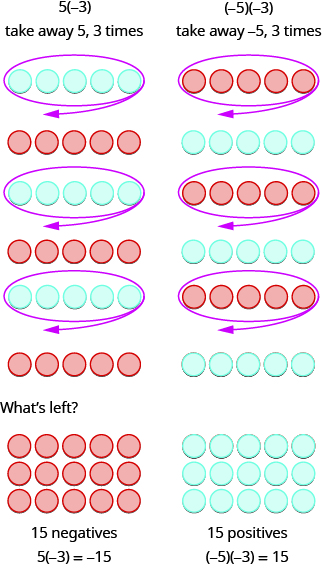
Підсумовуючи:
\[\begin{array}{ll} 5·3=15 & −5(3)=−15 \\ 5(−3)=−15 & (−5)(−3)=15 \end{array}\]
Зверніть увагу, що для множення двох знакових чисел, коли
\[ \text{signs are the } \textbf{same} \text{, the product is } \textbf{positive.} \\ \text{signs are } \textbf{different} \text{, the product is } \textbf{negative.} \]
А як щодо поділу? Ділення - обернена операція множення. Так,\(15÷3=5\) тому що\(15·3=15\). Словами цей вираз говорить про те, що 15 можна розділити на 3 групи по 5 кожна, тому що додавання п'яти три рази дає 15. Якщо ви подивитеся на деякі приклади множення цілих чисел, ви можете з'ясувати правила ділення цілих чисел.
\[\begin{array}{lclrccl} 5·3=15 & \text{so} & 15÷3=5 & \text{ } −5(3)=−15 & \text{so} & −15÷3=−5 \\ (−5)(−3)=15 & \text{so} & 15÷(−3)=−5 & \text{ } 5(−3)=−15 & \text{so} & −15÷(−3)=5 \end{array}\]
Ділення дотримується тих же правил, що і множення щодо знаків.
Для множення та ділення двох знакових чисел:
| ті ж ознаки | Результат |
|---|---|
| • Два позитиву | Позитивні |
| • Два негативу | Позитивні |
Якщо ознаки однакові, результат позитивний.
| Різні прикмети | Результат |
|---|---|
| • Позитивні і негативні | Негативний |
| • Негативні та позитивні | Негативний |
Якщо ознаки різні, результат негативний.
Множимо або ділимо: ⓐ\(−100÷(−4)\) ⓑ\(7⋅6\) ⓒ\(4(−8)\) ⓓ\(−27÷3.\)
- Відповідь
-
ⓐ
\(\begin{array}{lc} \text{} & −100÷(−4) \\ \text{Divide, with signs that are} \\ \text{the same the quotient is positive.} & 25 \end{array}\)
ⓑ
\(\begin{array} {lc} \text{} & 7·6 \\ \text{Multiply, with same signs.} & 42 \end{array}\)
ⓒ
\(\begin{array} {lc} \text{} & 4(−8) \\ \text{Multiply, with different signs.} & −32 \end{array}\)
ⓓ
\(\begin{array}{lc} \text{} & −27÷3 \\ \text{Divide, with different signs,} \\ \text{the quotient is negative.} & −9 \end{array}\)
Множимо або ділимо: ⓐ\(−115÷(−5)\) ⓑ\(5⋅12\) ⓒ\(9(−7)\) ⓓ\(−63÷7.\)
- Відповідь
-
ⓐ 23 ⓑ 60 ⓒ −63 ⓓ −9
Множимо або ділимо: ⓐ\(−117÷(−3)\) ⓑ\(3⋅13\) ⓒ\(7(−4)\) ⓓ\(−42÷6\).
- Відповідь
-
ⓐ 39 ⓑ 39 ⓒ −28 ⓓ −7
Коли ми множимо число на 1, в результаті виходить таке ж число. Кожен раз, коли ми множимо число на −1, отримуємо його протилежність!
\[−1a=−a\]
Множення числа на\(−1\) дає його протилежність.
Спрощення виразів цілими числами
Що відбувається, коли у виразі більше двох чисел? Порядок операцій все ще застосовується при включенні негативів. Пам'ятайте, будь ласка, вибачте мою дорогу тітку Саллі?
Спробуємо кілька прикладів. Ми спростимо вирази, які використовують усі чотири операції з цілими числами - додавання, віднімання, множення та ділення. Не забувайте стежити за порядком операцій.
Спрощення: ⓐ\((−2)^4\) ⓑ\(−2^4\).
- Відповідь
-
Зверніть увагу на різницю частин (а) і (б). У частині (a) показник означає підняти те, що знаходиться в дужках, −2 до 4-го степеня. У частині (b), експонента означає підняти лише 2 до 4-ї потужності, а потім прийняти протилежне.
ⓐ
\(\begin{array}{lc} \text{} & (−2)^4 \\ \text{Write in expanded form.} & (−2)(−2)(−2)(−2) \\ \text{Multiply.} & 4(−2)(−2) \\ \text{Multiply.} & −8(−2) \\ \text{Multiply.} & 16 \end{array}\)ⓑ
\(\begin{array}{lc} \text{} & −2^4 \\ \text{Write in expanded form.} & −(2·2·2·2) \\ \text{We are asked to find} & \text{} \\ \text{the opposite of }24. & \text{} \\ \text{Multiply.} & −(4·2·2) \\ \text{Multiply.} & −(8·2) \\ \text{Multiply.} & −16 \end{array}\)
Спрощення: ⓐ\((−3)^4\) ⓑ\(−3^4\).
- Відповідь
-
ⓐ 81 ⓑ −81
Спрощення: ⓐ\((−7)^2\) ⓑ\(−7^2\).
- Відповідь
-
ⓐ 49 ⓑ −49
Останній приклад показав нам різницю між\((−2)^4\) і\(−2^4\). Ця відмінність важлива для запобігання майбутніх помилок. Наступний приклад нагадує нам множити і ділити по порядку зліва направо.
Спрощення: ⓐ\(8(−9)÷(−2)^3\) ⓑ\(−30÷2+(−3)(−7)\).
- Відповідь
-
ⓐ
\(\begin{array}{lc} \text{} & 8(−9)÷(−2)^3 \\ \text{Exponents first.} & 8(−9)÷(−8) \\ \text{Multiply.} & −72÷(−8) \\ \text{Divide.} & 9 \end{array}\)
ⓑ
\(\begin{array}{lc} \text{} & −30÷2+(−3)(−7) \\ \text{Multiply and divide} \\ \text{left to right, so divide first.} & −15+(−3)(−7) \\ \text{Multiply.} & −15+21 \\ \text{Add.} & 6 \end{array}\)
Спрощення: ⓐ\(12(−9)÷(−3)^3\) ⓑ\(−27÷3+(−5)(−6).\)
- Відповідь
-
ⓐ 4 ⓑ 21
Спрощення: ⓐ\(18(−4)÷(−2)^3\) ⓑ\(−32÷4+(−2)(−7).\)
- Відповідь
-
ⓐ 9 ⓑ 6
Оцінити змінні вирази з цілими числами
Пам'ятайте, що оцінювати вираз означає підставити число для змінної у виразі. Тепер ми можемо використовувати як негативні числа, так і позитивні числа.
Оцініть\(4x^2−2xy+3y^2\), коли\(x=2,y=−1\).
- Відповідь
-
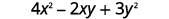
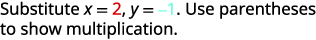
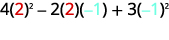
Спрощення експонентів. 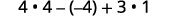
Помножити. 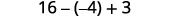
Відніміть. 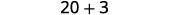
Додати. 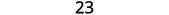
Оцініть:\(3x^2−2xy+6y^2\) коли\(x=1,y=−2\).
- Відповідь
-
31
Оцініть:\(4x^2−xy+5y^2\) коли\(x=−2,y=3\).
- Відповідь
-
67
Перекладіть фрази на вирази з цілими числами
Наша попередня робота з перекладу англійської на алгебру також стосується фраз, які включають як позитивні, так і негативні числа.
Перекласти і спростити: сума 8 і −12, збільшена на 3.
- Відповідь
-
\(\begin{array}{lc} \text{} & \text{the } \textbf{sum } \underline{\text{of}} \; –8 \; \underline{\text{and}} −12 \text{ increased by } 3 \\ \text{Translate.} & [8+(−12)]+3 \\ \text{Simplify. Be careful not to confuse the} \; \; \; \; \; \; \; \; \; \; & (−4)+3 \\ \text{brackets with an absolute value sign.} \\ \text{Add.} & −1 \end{array}\)
Перекласти і спростити суму 9 і −16, збільшену на 4.
- Відповідь
-
\((9+(−16))+4;−3\)
Перекласти та спростити суму −8 та −12, збільшену на 7.
- Відповідь
-
\((−8+(−12))+7;−13\)
Використання цілих чисел у програмах
Ми намітимо план вирішення додатків. Важко щось знайти, якщо ми не знаємо, що ми шукаємо або як це назвати! Тому, коли ми вирішуємо додаток, нам спочатку потрібно визначити, що проблема просить нас знайти. Потім ми напишемо фразу, яка дає інформацію, щоб знайти її. Ми переведемо фразу в вираз, а потім спростимо вираз, щоб отримати відповідь. Нарешті, ми підсумовуємо відповідь у реченні, щоб переконатися, що це має сенс.
Температура в Кендаллвіллі, штат Індіана одного ранку становила 11 градусів. До середини дня температура опустилася до −9−9 градусів. Яка різниця в ранковій та післяобідній температурах?
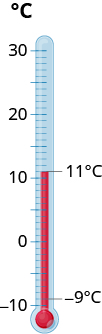
- Відповідь
-






Температура в Анкориджі, штат Аляска, одного ранку становила 15 градусів. До середини дня температура опустилася до 30 градусів морозу. Яка різниця в ранковій та післяобідній температурах?
- Відповідь
-
Різниця температур становила 45 градусів за Фаренгейтом.
Температура в Денвері становила −6 градусів в обідній час. До заходу сонця температура опустилася до −15 градусів. У чому полягала різниця в обідній і західній температурах?
- Відповідь
-
Різниця температур становила 9 градусів.
- Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі.
- Визначте, що нас просять знайти.
- Напишіть фразу, яка дає інформацію, щоб знайти її.
- Переведіть фразу на вираз.
- Спростити вираз.
- Відповісти на питання повним реченням.
Отримайте доступ до цього онлайн-ресурсу для додаткової інструкції та практики з цілими числами.
- Віднімання цілих чисел за допомогою лічильників
Ключові концепції
- \[\begin{align} & −a \text{ means the opposite of the number }a \\ & \text{The notation} −a \text{ is read as “the opposite of }a \text{.”} \end{align} \]
- Абсолютне значення числа - це його відстань від 0 на числовому рядку.
Абсолютне значення числа n записується як\(|n|\) і\(|n|≥0\) для всіх чисел.
Абсолютні значення завжди більше або рівні нулю.
- \[\begin{array}{lclc} \text{Parentheses} & () & \text{Braces} & \{ \} \\ \text{Brackets} & [] & \text{Absolute value} & ||\end{array}\]
- Властивість віднімання
\(a−b=a+(−b)\)
Віднімання числа - це те саме, що і додавання його протилежності. - Для множення та ділення двох знакових чисел:
Якщо ознаки однакові, результат позитивний.ті ж ознаки Результат • Два позитиву Позитивні • Два негативу Позитивні
Якщо ознаки різні, результат негативний.Різні прикмети Результат • Позитивні і негативні Негативний • Негативні та позитивні Негативний - Множення на\(−1\)
\(−1a=−a\)
Множення числа на\(−1\) дає його протилежність.
- Як використовувати цілі числа в додатках.
- Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі
- Визначте, що нас просять знайти.
- Напишіть фразу, яка дає інформацію, щоб знайти її.
- Переведіть фразу на вираз.
- Спростити вираз.
- Відповісти на питання повним реченням.
Глосарій
- абсолютне значення
- Абсолютне значення числа - це його відстань від\(0\) на числовому рядку.
- цілих чисел
- Цілі числа і їх протилежності називаються цілими числами.
- від'ємні числа
- Числа менше, ніж\(0\) від'ємні числа.
- навпроти
- Протилежність числу - це число, яке на тій же відстані від нуля на числовій лінії, але на протилежній стороні нуля.
