1.2E: Вправи

Last updated
Save as PDF

Page ID: 59592

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Практика робить досконалим

Визначте множники та коефіцієнти

У наступних вправах використовуйте тести на подільність, щоб визначити, чи ділиться кожне число на 2, на 3, на 5, на 6 та на 10.

1. $84$

Відповідь: Ділимо на 2, 3, 6

2. $96$

3. $896$

Відповідь: Ділиться на 2

4. $942$

5. $22,335$

Відповідь: Ділиться на 3, 5

6. $39,075$

Пошук простих факторизацій та найменш поширених кратних

У наступних вправах знайдіть просту факторизацію.

7. $86$

Відповідь: $2⋅43$

8. $78$

9. $455$

Відповідь: $5⋅7⋅13$

10. $400$

11. $432$

Відповідь: $2⋅2⋅2⋅2⋅3⋅3⋅3$

12. $627$

У наступних вправах знайдіть найменш поширене кратне кожної пари чисел за допомогою методу простих множників.

13. $8,\; 12$

Відповідь: $24$

14. $12,\; 16$

15. $28,\; 40$

Відповідь: $280$

16. $84, \;90$

17. $55, \;88$

Відповідь: $440$

18. $60, \;72$

Спрощення виразів за допомогою порядку операцій

У наступних вправах спрощуйте кожен вираз.

19. $2^3−12÷(9−5)$

Відповідь: $5$

20. $3^2−18÷(11−5)$

21. $2+8(6+1)$

Відповідь: $58$

22. $4+6(3+6)$

23. $20÷4+6(5−1)$

Відповідь: $29$

24. $33÷3+4(7−2)$

25. $3(1+9⋅6)−4^2$

Відповідь: $149$

26. $5(2+8⋅4)−7^2$

27. $2[1+3(10−2)]$

Відповідь: $50$

28. $5[2+4(3−2)]$

29. $8+2[7−2(5−3)]−3^2$

Відповідь: $5$

30. $10+3[6−2(4−2)]−2^4$

Оцінити вираз

У наступних вправах оцініть наступні вирази.

31. Коли$x=2$,

а.$x^6$

б.$4^x$

c.$2x^2+3x−7$

Відповідь: а. 64
б. 16
с. 7

32. Коли$x=3$,

а.$x^5$

б.$5x$

c.$3x^2−4x−8$

33. Коли$x=4$ і$y=1$

$x^2+3xy−7y^2$

Відповідь: $21$

34. Коли$x=3$ і$y=2$

$6x^2+3xy−9y^2$

35. Коли$x=10$ і$y=7$

$(x−y)^2$

Відповідь: $9$

36. Коли$a=3$ і$b=8$

$a^2+b^2$

Спростіть вирази, поєднуючи подібні терміни

У наступних вправах спростіть наступні вирази, комбінуючи подібні терміни.

37. $7x+2+3x+4$

Відповідь: $10x+6$

38. $8y+5+2y−4$

39. $10a+7+5a−2+7a−4$

Відповідь: $22a+1$

40. $7c+4+6c−3+9c−1$

41. $3x^2+12x+11+14x^2+8x+5$

Відповідь: $17x^2+20x+16$

42. $5b^2+9b+10+2b^2+3b−4$

Перекласти англійську фразу на алгебраїчний вираз

У наступних вправах переводите фрази в алгебраїчні вирази.

43. а. різниця$5x^2$ і$6xy$

b. частка$6y^2$ і$5x$

c. двадцять один більше$y^2$

d.$6x$ менше$81x^2$

Відповідь

а.$5x^2−6xy$ б.$\frac{6y^2}{5x}$

в.$y^2+21$ д.$81x^2−6x$

44. а. різниця$17x^2$ і$17x^2$ і$5xy$

b. частка$8y^3$ і$3x$

c. вісімнадцять більше$a^2$;

d.$11b$ менше$100b^2$

45. а. сума$4ab^2$ і$3a^2b$

b. продукт$4y^2$ і$5x$

c. п'ятнадцять більше$m$

d.$9x$ менше$121x^2$

Відповідь

а.$4ab^2+3a^2b$ б.$20xy^2$

в.$m+15$ д.$121x^2−9x$$9x<121x^2$

46. а. сума$3x^2y$ і$7xy^2$

b. продукт$6xy^2$ і$4z$

c. дванадцять більше$3x^2$

d.$7x^2$ менше$63x^3$

47. а. у вісім разів різниця$y$ і дев'ять

b. різниця у вісім разів$y$ і$9$

Відповідь: а.$8(y−9)$
б.$8y−9$

48. а. в сім разів різниця$y$ і один

b. різниця в сім разів$y$ і$1$

49. а. в п'ять разів перевищує суму$3x$ і$y$

б. сума в п'ять разів$3x$ і$y$

Відповідь: а.$5(3x+y)$
б.$15x+y$

50. а. одинадцять разів перевищує суму$4x2$ і$5x$

б. сума одинадцяти разів$4x^2$ і$5x$

51. Ерік має рок і кантрі пісні у своєму плейлисті. Кількість рок-пісень на 14 більше, ніж в два рази перевищує кількість кантрі-пісень. Нехай c представляють кількість пісень кантрі. Напишіть вираз для кількості рок-пісень.

Відповідь: $14>2c$

52. Кількість жінок у класі статистики на 8 більше, ніж удвічі більше, ніж у чоловіків. $m$Дозволяти представляти кількість чоловіків. Напишіть вираз для кількості жінок.

53. У Грега в кишені нікельси і копійки. Кількість копійок на сім менше, ніж три числа нікелів. Нехай n позначає кількість нікелів. Напишіть вираз на кількість копійок.

Відповідь: $3n-7$

54. Жаннет має$$5$ і$$10$ купюри в гаманці. Кількість п'ятірок в три більше, ніж в шість разів перевищує кількість десятків. $t$Дозволяти представляти кількість десятків. Напишіть вираз для числа п'ятірок.

Письмові вправи

55. Поясніть своїми словами, як знайти просту факторизацію складеного числа.

Відповідь: Відповіді будуть відрізнятися.

56. Чому важливо використовувати порядок операцій для спрощення виразу?

57. Поясніть, як ви ідентифікуєте подібні терміни у виразі$8a^2+4a+9−a^2−1.$

Відповідь: Відповіді будуть відрізнятися.

58. Поясніть різницю між фразами «4 рази сума x і y» і «сума в 4 рази x і y».

Самостійна перевірка

a Використовуйте цей контрольний список, щоб оцінити ваше володіння цілями цього розділу.

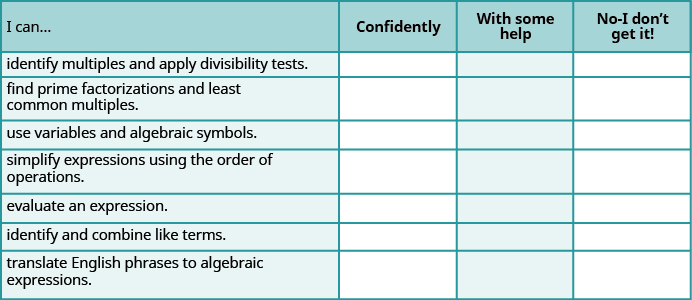
$Ця таблиця має 4 стовпці, 7 рядків і рядок заголовка. Рядок заголовка позначає кожен стовпець, який я можу, впевнено, з деякою допомогою і ні, я не розумію. Перший стовпець має такі твердження: визначити кратні і застосувати тести подільності, знайти прості множники і найменш поширені множники, використовувати змінні і алгебраїчні символи, спростити вирази за допомогою порядку операцій, оцінити вираз, визначити і комбінувати подібні терміни, перекладати англійську фрази до алгебраїчних виразів. Решта стовпці порожні.$

б Якщо більшість ваших перевірок були:

... впевнено. Вітаємо! Ви досягли цілей у цьому розділі. Подумайте про навички навчання, які ви використовували, щоб ви могли продовжувати їх використовувати. Що ви зробили, щоб стати впевненим у своїй здатності робити ці речі? Будьте конкретні.

... з деякою допомогою. Це потрібно вирішувати швидко, оскільки теми, які ви не освоюєте, стають вибоїнами на вашому шляху до успіху. У математиці кожна тема будується на попередній роботі. Важливо переконатися, що у вас міцний фундамент, перш ніж рухатися далі. До кого можна звернутися за допомогою? Ваші колеги-однокласники та інструктор - хороші ресурси. Чи є в кампусі місце, де доступні репетитори з математики? Чи можна вдосконалити свої навички навчання?

... ні - я не розумію! Це попереджувальний знак, і ви не повинні його ігнорувати. Ви повинні отримати допомогу відразу ж, інакше ви швидко будете перевантажені. Зверніться до інструктора, як тільки зможете обговорити вашу ситуацію. Разом ви можете придумати план, щоб отримати вам необхідну допомогу.