9.2: Властивості множення радикалів

Нагадаємо, що рівняння$x^2 = a$, де a - додатне дійсне число, має два рішення, як зазначено на малюнку 1.

Малюнок 1. Рівняння$x^2 = a$, де a - додатне дійсне число, має два розв'язки.

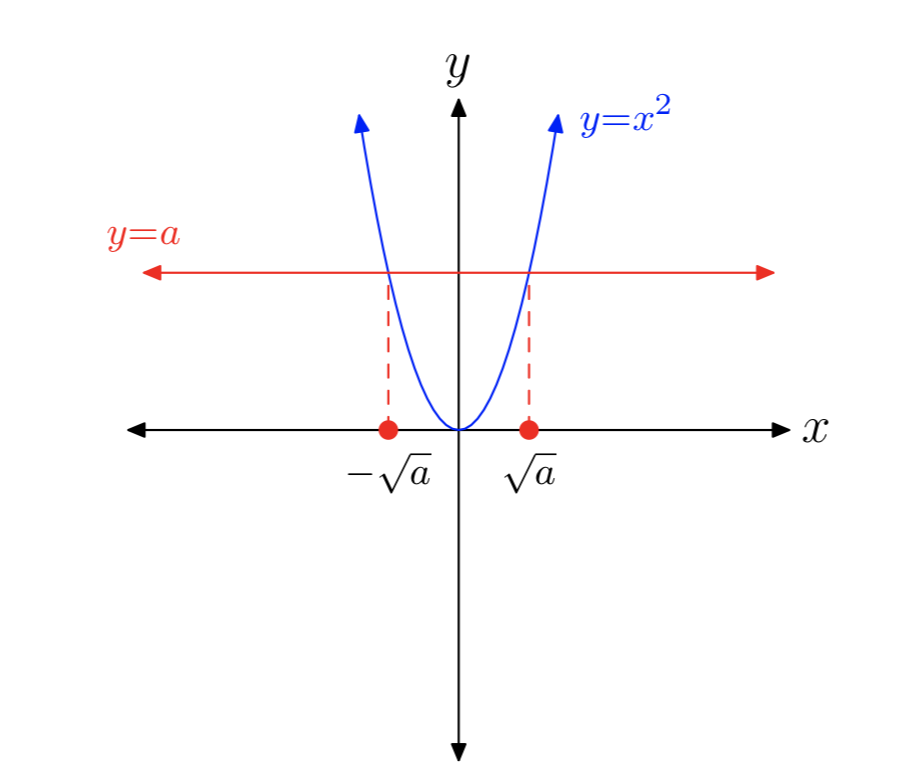
Ось ключові факти.

Рішення

Рішення$x^2 = a$. Якщо a - додатне дійсне число, то:

1. Рівняння$x^2 = a$ має два реальних рішення.
2. Позначення$\sqrt{a}$ позначають унікальне позитивне реальне рішення.
3. Позначення$−\sqrt{a}$ позначають унікальне негативне дійсне рішення.

Зверніть увагу на використання слова unique. Коли ми говоримо, що рішення$\sqrt{a}$ є унікальним позитивним реальним рішенням, ми маємо на увазі, що воно єдине. Немає інших позитивних дійсних чисел, які є розв'язками$x^2 = a$. Подібне твердження стосується унікального негативного рішення.

Таким чином, рівняння$x^2 = a$ $x^2 = b$мають унікальні позитивні розв'язки$x = \sqrt{a}$ і$x = \sqrt{b}$, відповідно, передбачають, що a і b є додатними дійсними числами. Крім того, оскільки вони є розв'язками, їх можна замінити в рівняння$x^2 = a$ та$x^2 = b$ отримати результати

$(\sqrt{a})^2 = a$і$(\sqrt{b})^2 = b$

відповідно. Знову ж таки, ці результати залежать від того, що a і b є позитивними дійсними числами.

Аналогічно рівняння

$x^2 = ab$

має унікальне позитивне рішення$x = \sqrt{ab}$, за умови, що a і b є додатними числами. Однак зауважте, що

$(\sqrt{a}\sqrt{b})^2 = (\sqrt{a})^{2}(\sqrt{b})^{2} = ab$,

прийняття другого$\sqrt{a}\sqrt{b}$ позитивного рішення$x^2 = ab$. Однак, оскільки$\sqrt{ab}$ є унікальним позитивним рішенням$x^2 = ab$, це змушує

$\sqrt{ab} = \sqrt{a}\sqrt{b}$

Ця дискусія призводить до наступного властивості радикалів.

Нерухомість 1

$b$Дозволяти$a$ і бути позитивними дійсними числами. Потім,

$$\sqrt{ab} = \sqrt{a}\sqrt{b}$$

Цей результат можна використовувати двома чітко різними способами.

• Ви можете використовувати результат для множення двох квадратних коренів, як в

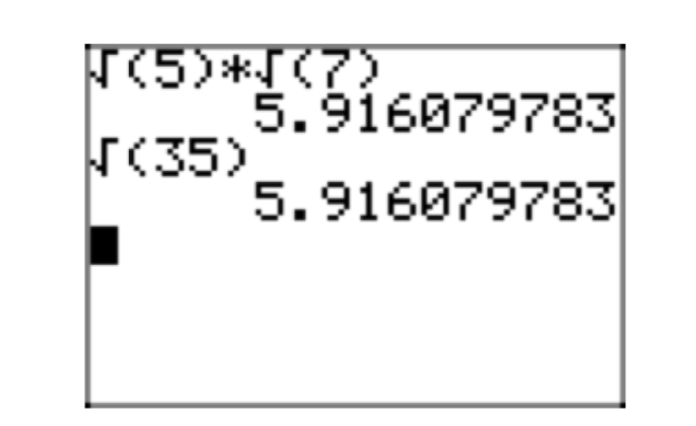
  $\sqrt{7}\sqrt{5} = \sqrt{35}$.

• $\sqrt{35} = \sqrt{7}\sqrt{5}$

Цікаво перевірити цей результат на калькуляторі, як показано на малюнку 2.

Малюнок 2. Перевірка результату$\sqrt{5}\sqrt{7} = \sqrt{35}$

Проста радикальна форма

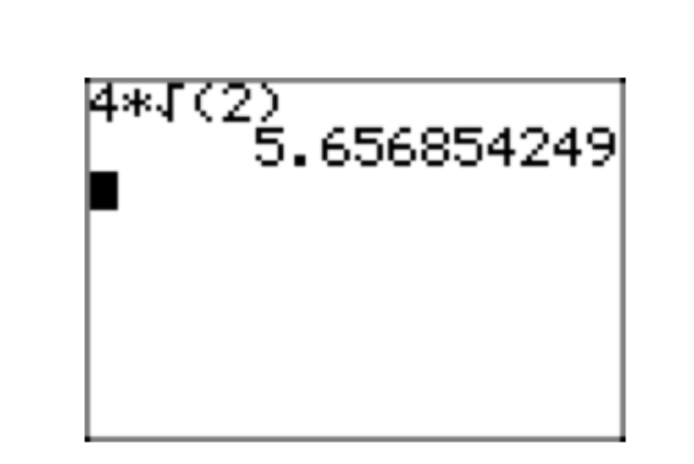
У цьому розділі ми введемо поняття простої радикальної форми, але давайте спочатку почнемо з невеликого розповіді. Марта та Девід навчаються разом, працюючи над домашньою задачею зі свого підручника. Марта приїхала до відповіді$\sqrt{32}$, поки Девід отримує результат$2\sqrt{8}$. Спочатку Девід і Марта вважають, що їхні рішення - це різні числа, але вони помилялися раніше, тому вони вирішили порівняти десяткові наближення своїх результатів на своїх калькуляторах. Результат Марти показаний на малюнку 3 (а), тоді як Давид показаний на малюнку 3 (b).

Малюнок 3. Порівняння$\sqrt{32}$ с$2\sqrt{8}$.

Марта знаходить це,$\sqrt{32} \approx 5.656854249$ і Девід знаходить, що його рішення$2\sqrt{8} \approx 5.656854249$. Девід і Марта роблять висновок, що їхні рішення збігаються, але вони хочуть знати, чому два дуже різних радикальних вирази ідентичні.

Наступний розрахунок, використовуючи Property 1, показує, чому результат Девіда ідентичний результату Марти.

$\sqrt{32}=\sqrt{4}\sqrt{8}=2\sqrt{8}$

Дійсно, є навіть третя можливість, така, яка сильно відрізняється від результатів, знайдених Девідом і Мартою. Розглянемо наступний розрахунок, який знову використовує Property 1.

$\sqrt{32}=\sqrt{16}\sqrt{2}=4\sqrt{2}$

На малюнку 4 зверніть увагу, що десяткове$4\sqrt{2}$ наближення наближень для$\sqrt{32}$ (результат Марти на рис. 3 (а)) і$2\sqrt{8}$ (результат Давида на малюнку 3 (b)).

Малюнок 4. Наближення$4\sqrt{2}$.

Хоча всі три з цих радикальних виразів ($\sqrt{32}$$2\sqrt{8}$, і$4\sqrt{2}$) ідентичні, дещо неприємно мати стільки різних форм, особливо коли ми хочемо порівняти рішення. Тому пропонуємо набір рекомендацій для спеціальної форми відповіді, яку ми назвемо простою радикальною формою.

Перше керівництво для простої радикальної форми.

Коли це можливо, врахуйте ідеальний квадрат.

Таким чином,$\sqrt{32}$ не в простій радикальній формі, так як можна виділити ідеальний квадрат, як в

$\sqrt{32}=\sqrt{16}\sqrt{2}=4\sqrt{2}$.

Аналогічно, результат$(2\sqrt{8})$ Девіда не в простій радикальній формі, тому що він теж може зарахувати ідеальний квадрат наступним чином.

$2\sqrt{8}=2(\sqrt{4}\sqrt{2})=2(2\sqrt{2})=(2 \cdot 2)\sqrt{2}=4\sqrt{2}$.

Якщо і Марта, і Девід дотримуються «першого орієнтиру для простої радикальної форми», їх відповідь буде виглядати однаково (обидва рівні$4\sqrt{2}$). Це одне з першочергових переваг простої радикальної форми: здатність порівнювати рішення.

У наступних прикладах (і у вправах) корисно, якщо ви знаєте квадрати перших 25 натуральних чисел. Ми перерахували їх у полі для вас у таблиці 1 для подальшого використання.

Помістимо ще кілька радикальних виразів в простій радикальній формі.

Приклад$\PageIndex{3}$

Місце$\sqrt{50}$ в простій радикальній формі.

Відповідь

У таблиці 1, 25 - квадрат. Тому що$50 = 25 \cdot 2$, ми можемо використовувати властивість 1, щоб написати

$\sqrt{50}=\sqrt{25}\sqrt{2}=5\sqrt{2}$.

Приклад$\PageIndex{4}$

Місце$\sqrt{98}$ в простій радикальній формі.

Відповідь

У таблиці 1, 49 - квадрат. Тому що$98 = 49 \cdot 2$, ми можемо використовувати властивість 1, щоб написати

$\sqrt{98}=\sqrt{49}\sqrt{2}=7\sqrt{2}$.

Приклад$\PageIndex{5}$

Місце$\sqrt{288}$ в простій радикальній формі.

Відповідь

Деякі студенти, здається, здатні вирвати з повітря оптимальний «ідеальний квадрат». Якщо ви звернетеся до таблиці 1, ви зауважте, що 144 - це квадрат. Тому що$288 = 144 \cdot 2$, ми можемо написати

$\sqrt{288}=\sqrt{144}\sqrt{2}=12\sqrt{2}$.

Однак, що робити, якщо ви пропустите цей вищий ідеальний квадрат$288 = 4 \cdot 72$, подумайте і напишіть

$\sqrt{288}=\sqrt{4}\sqrt{72}=2\sqrt{72}$.

Цей підхід не є неправильним, якщо ви розумієте, що ви ще не закінчили. Ви все ще можете врахувати ідеальний квадрат із 72. Тому що$72 = 36 \cdot 2$, можна продовжувати і писати

$2\sqrt{72}=2(\sqrt{36}\sqrt{2})=2(6\sqrt{2})=(2\cdot 6)\sqrt{2}=12\sqrt{2}$.

Відзначимо, що ми прийшли до тієї ж простої радикальної форми, а саме$12\sqrt{2}$. Це зайняло у нас трохи більше часу. Поки ми розуміємо, що ми повинні продовжувати, поки ми більше не зможемо зарахувати ідеальний квадрат, ми прийдемо до тієї ж простої радикальної форми, що і студент, який, здається, чарівним чином витягує вищий квадрат з повітря.

Дійсно, ось ще один підхід, який однаково справедливий.

$\sqrt{288}=\sqrt{4}\sqrt{72}=2(\sqrt{4}\sqrt{18})=2(2\sqrt{18})=(2\cdot 2)\sqrt{18}=4\sqrt{18}$

Нам потрібно визнати, що ми все ще не закінчили, тому що ми можемо витягти ще один ідеальний квадрат наступним чином.

$4\sqrt{18}=4(\sqrt{9}\sqrt{2})=4(3\sqrt{2})=(4\cdot 3)\sqrt{2}=12\sqrt{2}$

Ще раз той же результат. Однак зауважте, що нам належить витягти найбільший квадрат, оскільки це мінімізує кількість кроків, необхідних для досягнення простої радикальної форми.

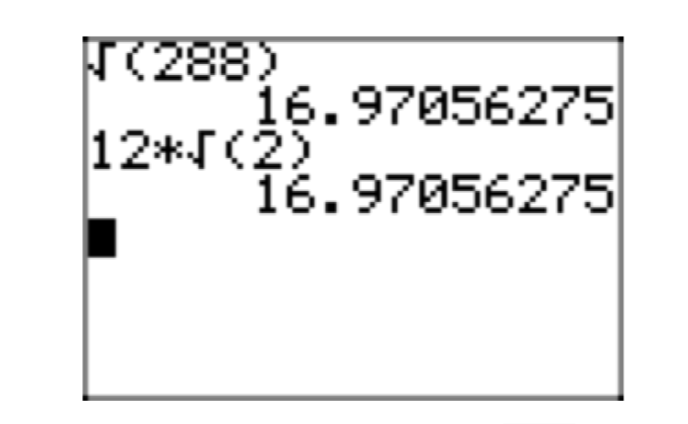
Перевірка результатів за допомогою графічного калькулятора. Після того, як ви розмістили радикальний вираз у простій радикальній формі, ви можете скористатися графічним калькулятором, щоб перевірити результат. У цьому прикладі ми виявили, що

$\sqrt{288}=12\sqrt{2}$. (6)

Введіть ліву та праву сторони цього результату, як показано на малюнку 5. Зверніть увагу, що кожен

сторона виробляє таке ж десяткове наближення, перевіряючи результат в рівнянні (6).

Малюнок 5. Порівнюючи$\sqrt{288}$ з його простою радикальною формою$12\sqrt{2}$.

Корисні поради

Нагадаємо, що підвищення потужності бази до іншої потужності вимагає, щоб ми помножили показники.

Підняття сили бази до іншої держави.

$(a^m)^n = a^{mn}$

Зокрема, коли ви квадратуєте ступінь основи, ви повинні помножити показник на 2. Наприклад,

$(2^5)^2 = 2^{10}$.

І навпаки, оскільки беручи квадратний корінь є «зворотним» квадратом, при прийнятті квадратного кореня ми повинні розділити існуючий показник на 2, як у

$\sqrt{2^{10}} = 2^5$.

Зверніть увагу, що квадрат$2^5$ дає$2^{10}$, тому беручи квадратний корінь з$2^{10}$ повинен повернути вас$2^5$. Коли ви квадрат, ви подвоюєте показник. Тому, коли ви берете квадратний корінь, ви повинні зменшити показник вдвічі.

Аналогічно,

• $(2^6)^2 = 2^{12}$так$\sqrt{2^{12}} = 2^6$.
• $(2^7)^2 = 2^{14}$так$\sqrt{2^{14}} = 2^7$.
• $(2^8)^2 = 2^{16}$так$\sqrt{2^{16}} = 2^8$.

Це призводить до наступного результату.

Беручи квадратний корінь парної сили.

При прийнятті квадратного кореня$x^n$, коли x - додатне дійсне число, а n - парне натуральне число, розділіть показник на два. В символах,

$\sqrt{x^n} = x^{\frac{n}{2}}$.

Зауважте, що це узгоджується з визначенням раціональних показників, представленим у главі 8, як у

$\sqrt{x^n} = (x^n)^{\frac{1}{2}} = x^{\frac{n}{2}}$.

З іншого боку, нагадаємо, що підвищення продукту до влади вимагає, щоб ми піднімали кожен фактор до цієї сили.

Підняття продукту до влади.

$(ab)^n = a^{n}b^{n}$.

Зокрема, якщо ви квадратуєте продукт, ви повинні квадратувати кожен фактор. Наприклад,

$(5^{3}7^{4})^2 = (5^3)^{2}(7^4)^2 = 5^{6}7^{8}$.

Зверніть увагу, що ми помножили кожен існуючий показник у цьому добутку на 2.

Властивість 1 аналогічна тим, що коли ми беремо квадратний корінь продукту, ми беремо квадратний корінь кожного фактора. Оскільки беручи квадратний корінь є зворотним квадратом, ми повинні розділити кожен існуючий показник на 2, як у

$\sqrt{5^{6}7^{8}} = \sqrt{5^{6}}\sqrt{7^{8}} = 5^{3}7^{4}$

Давайте розглянемо кілька прикладів, в яких використовується дана техніка.

Приклад$\PageIndex{7}$

Спростити$\sqrt{2^{4}3^{6}5^{10}}$

Відповідь

Беручи квадратний корінь добутку експоненціальних факторів, розділіть кожну експоненту на 2.

$\sqrt{2^{4}3^{6}5^{10}} = 2^{2}3^{3}5^{5}$

При необхідності можна розширити експоненціальні коефіцієнти і помножити, щоб отримати єдиний числовий відповідь.

$2^{2}3^{3}5^{5} = 4 \cdot 27 \cdot 3125 = 337500$

Для отримання остаточного рішення використовувався калькулятор.

Приклад$\PageIndex{8}$

Спростити$\sqrt{2^{5}3^{3}}$

Відповідь

У цьому прикладі складність полягає в тому, що показники не діляться на 2. Однак, якщо можливо, «перший орієнтир простої радикальної форми» вимагає, щоб ми зарахували ідеальний квадрат. Отже, витягніть кожен фактор, піднятий до максимально можливої потужності, яка ділиться на 2, як в

$\sqrt{2^{5}3^{3}} = \sqrt{2^{4}3^{2}}\sqrt{2 \cdot 3}$

Тепер розділіть кожну експоненту на 2.

$\sqrt{2^{4}3^{2}}\sqrt{2\cdot 3} = 2^{2}3^{1}\sqrt{2 \cdot 3}$

Нарешті, спростити шляхом розширення кожного експоненціального коефіцієнта та множення.

$2^{2}3^{1}\sqrt{2 \cdot 3} = 4 \cdot 3\sqrt{2 \cdot 3} = 12\sqrt{6}$

Приклад$\PageIndex{9}$

Спростити$\sqrt{3^{7}5^{2}7^{5}}$.

Відповідь

Витягніть кожен фактор до максимально можливої потужності, яка ділиться на 2.

$\sqrt{3^{7}5^{2}7^{5}} = \sqrt{3^{6}5^{2}7^{4}}\sqrt{3 \cdot 7}$

Розділіть кожну експоненту на 2.

$\sqrt{3^{6}5^{2}7^{4}}\sqrt{3 \cdot 7} = 3^{3}5^{1}7^{2}\sqrt{3 \cdot 7}$

Розгорніть кожен експоненціальний коефіцієнт і помножте.

$3^{3}5^{1}7^{2}\sqrt{3 \cdot 7} = 27 \cdot 5 \cdot 49 \sqrt{3 \cdot 7} =6615\sqrt{21}$

Приклад$\PageIndex{10}$

Місце$\sqrt{216}$ в простій радикальній формі.

Якщо ми просте множник 216, ми можемо атакувати цю проблему з тією ж технікою, яка використовувалася в попередніх прикладах. Перш ніж ми простий фактор 216, ось кілька тестів на подільність, які вам можуть виявитися корисними.

Тест на подільність

• Якщо число закінчується на 0, 2, 4, 6 або 8, воно є парним числом і ділиться на 2.
• Якщо останні дві цифри числа утворюють число, яке ділиться на 4, то все число ділиться на 4.
• Якщо число закінчується на 0 або 5, воно ділиться на 5.
• Якщо сума цифр числа ділиться на 3, то все число ділиться на 3.
• Якщо сума цифр числа ділиться на 9, то все число ділиться на 9.

Наприклад, для того, щоб:

• Число 226 закінчується на 6, тому воно парне і ділиться на 2. Дійсно,$226 = 2 \cdot 113$.
• Останні дві цифри 224 - це 24, що ділиться на 4, тому все число ділиться на 4. Дійсно,$224 = 4 \cdot 56$.
• Остання цифра 225 - це 5. Тому 225 ділиться на 5. Дійсно,$225 = 5 \cdot 45$.
• Сума цифр 222 дорівнює 2 + 2 + 2 = 6, яка ділиться на 3. Тому 222 ділиться на 3. Дійсно,$222 = 3 \cdot 74$.
• Сума цифр 684 дорівнює 6 + 8 + 4 = 18, що ділиться на 9. Тому 684 ділиться на 9. Дійсно,$684 = 9 \cdot 76$.

Тепер давайте простий фактор 216. Зверніть увагу, що 2+1+6 = 9, тому 216 ділиться на 9. Дійсно,$216 = 9 \cdot 24$. На малюнку 6 ми використовуємо «дерево факторів» для продовження факторингу, поки всі «листя» не стануть простими числами.

Малюнок 6. Використання дерева факторів для простого множника 216

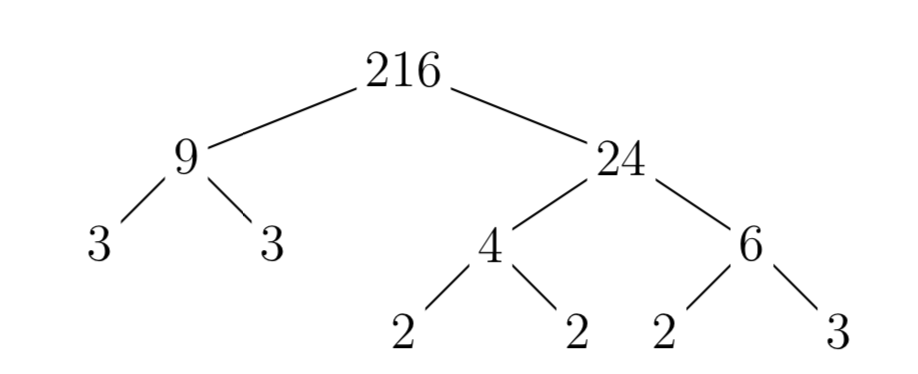
Таким чином,

$216 = 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 \cdot 3$,

або в експоненціальній формі,

$216 = 2^{3} \cdot 3^{3}$.

Таким чином,

$\sqrt{216} = \sqrt{2^{3}3^{3}} = \sqrt{2^{2}3^{2}}\sqrt{2\cdot 3}=2 \cdot 3\sqrt{2 \cdot 3}=6\sqrt{6}$.

Prime факторизація є неймовірно корисним інструментом!

Давайте розглянемо інший приклад.

Приклад$\PageIndex{11}$

Місце$\sqrt{2592}$ в простій радикальній формі.

Відповідь

Якщо ми знайдемо просту факторизацію для 2592, ми можемо атакувати цей приклад, використовуючи ту саму техніку, яку ми використовували в попередньому прикладі. Відзначимо, що сума цифр 2592 дорівнює 2 + 5 + 9 + 2 = 18, яка ділиться на 9. Тому 2592 також ділиться на 9.

$2592 = 9 \cdot 288$

Сума цифр 288 дорівнює 2+8+8 = 18, що ділиться на 9, тому 288 також ділиться на 9.

$2592 = 9 \cdot (9 \cdot 32)$

Продовжуйте таким чином, поки листя вашого «факторного дерева» не стануть простими. Тоді, ви повинні отримати

$2592 = 2^{5}3^{4}$.

Таким чином,

$\sqrt{2592} = \sqrt{2^{5}3^{4}} = \sqrt{2^{4}3^{4}}\sqrt{2} = 2^{2}3^{2}\sqrt{2} = 4 \cdot 9\sqrt{2}=36\sqrt{2}$.

Давайте скористаємося графічним калькулятором, щоб перевірити цей результат. Введіть кожну сторону$\sqrt{2592} = 36\sqrt{2}$ окремо і порівняйте наближення, як показано на малюнку 7.

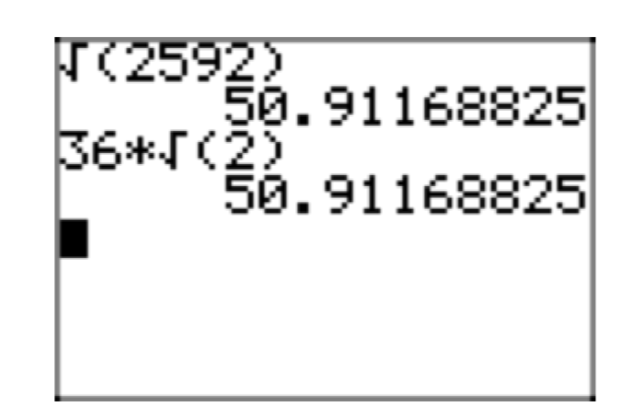
Малюнок 7. Порівнюючи$\sqrt{2592}$ з його простою радикальною формою$36\sqrt{2}$.

Важлива властивість квадратних коренів

Одна з найпоширеніших помилок в алгебрі виникає, коли практикуючих просять спростити вираз$\sqrt{x^2}$, де x - будь-яке довільне дійсне число. Розглянемо дві найпоширеніші помилки.

• Деякі стверджують, що наступне твердження вірно для будь-якого довільного дійсного числа x.

$\sqrt{x^2} = \pm x$.

Це легко помітити як неправильне. Просто підставити будь-яке дійсне число для x, щоб перевірити цю претензію. Ми виберемо x = 3 і підставимо його в кожну сторону запропонованого твердження.

$\sqrt{3^2} = \pm 3$.

Якщо спростити ліву сторону, то отримаємо наступний результат.

$\sqrt{3^2} = \pm 3$.

$3 = \pm 3$

Неправильно стверджувати, що 3 і$\pm 3$ рівні.

• Друга помилка полягає в тому, щоб стверджувати, що

$\sqrt{x^2} = x$

для будь-якого довільного дійсного числа x. Хоча це, безумовно, вірно, якщо ви підставите невід'ємні числа на x, подивіться, що станеться, коли ви підставите − 3 на x.

$\sqrt{(−3)^2} = 3$

Якщо спростити ліву сторону, то отримаємо наступний результат.

$\sqrt{9} = −3$

3 = −3

Зрозуміло, що 3 і − 3 не рівні.

В обох випадках забутий той факт, що$\sqrt{}$ вимагає позитивного (ненегативного, якщо ви хочете включити регістр$\sqrt{0}$) квадратний корінь. В обох вищезазначених помилках, а саме$\sqrt{x^2} = \pm x$ і$\sqrt{x^2} = x$, ліва сторона закликає до ненегативної відповіді, але нічого не зроблено, щоб застрахувати, що права сторона також ненегативна. Щось приходить на розум?

Звичайно, якщо ми обернути праву частину в абсолютних значеннях, як в

$\sqrt{x^2} = |x|$,

тоді обидві сторони закликають до ненегативної відповіді. Дійсно, зверніть увагу, що

$\sqrt{(−3)^2} =|−3|$,$\sqrt{0^2} =|0|$, і$\sqrt{3^2} =|3|$

всі дійсні твердження.

Це обговорення призводить до наступного результату.

Позитивний квадратний корінь квадрата x

Якщо x - будь-яке дійсне число, то

$\sqrt{x^2} = |x|$,

Наступне завдання - використовувати цю нову властивість для отримання надзвичайно корисної властивості абсолютного значення.

Властивість множення абсолютної величини

Якщо ми поєднаємо закон експонентів для квадратного виробу з нашою властивістю брати квадратний корінь продукту, ми можемо написати

$\sqrt{(ab)^2} = \sqrt{a^{2}b^{2}} = \sqrt{a^2}\sqrt{b^2}$.

Втім$\sqrt{(ab)^2} = |ab|$, поки$\sqrt{a^2}{b^2} = |a||b|$. Це обговорення призводить до наступного результату.

Правило продукту для абсолютного значення

Якщо a і b є будь-якими дійсними числами,

|аб| = |а||б|.

У словах абсолютна величина добутку дорівнює добутку абсолютних значень.

Ми бачили цю властивість раніше в розділі про функцію абсолютного значення, де ми надали інший підхід до доказу властивості. Цікаво, що ми можемо довести цю властивість абсолютно по-новому, використовуючи властивості квадратного кореня. Ми побачимо, що нам потрібно правило продукту для абсолютної вартості в наступних прикладах.

Наприклад, використовуючи правило продукту, якщо х є будь-яким дійсним числом, ми могли б написати

|3х| = |3||х| = 3|х|

Однак ми не можемо видалити смуги абсолютних значень, які оточують x, якщо ми не знаємо знак x Якщо$x \ge 0$, то |x| = x і вираз стає

3|х| = 3х.

З іншого боку, якщо x < 0, то |x| = −x і вираз стане

3|х| = 3 (−х) = −3х.

Давайте розглянемо інший приклад. Використовуючи правило продукту, якщо x є будь-яким дійсним числом, виразом$| − 4x^3|$ можна маніпулювати наступним чином.

$|−4x^3| = |−4||x^2||x|$

Однак |−4|=4 і оскільки$x^2 \ge 0$ для будь-якого значення x,$|x^2|=x^2$. Таким чином,

$|−4||x^2||x| = 4x^{2}|x|$.

Знову ж таки, немає ніякого способу ми можемо видалити абсолютні значення смуги навколо х$x \ge 0$, якщо ми не знаємо знак х, то|x|=x і

$4x^{2}|x| = 4x^{2}(x) = 4x^3$.

З іншого боку, якщо x < 0, то |x| = −x і

$4x^{2}|x| = 4x^{2}(−x) = −4x^3$.

Давайте використаємо ці ідеї, щоб спростити деякі радикальні вирази, які містять змінні.

Змінні вирази

Приклад$\PageIndex{13}$

Враховуючи, що x представляє будь-які дійсні числа, помістіть радикальний вираз

$\sqrt{48x^6}$

в простій радикальній формі.

Проста радикальна форма вимагає, щоб ми враховували ідеальний квадрат, якщо це можливо. У цьому випадку$48 = 16 \cdot 3$ і ми враховуємо найвищу потужність х, яка ділиться на 2.

$\sqrt{48x^6} = \sqrt{16x^6}\sqrt{3}$

Тепер ми можемо використовувати Property 1, щоб взяти квадратний корінь кожного фактора.

$\sqrt{16x^6}\sqrt{3} = \sqrt{16}\sqrt{x^6}\sqrt{3}$

Тепер запам'ятайте, що позначення$\sqrt{}$ вимагає невід'ємного квадратного кореня, тому ми повинні гарантувати, що кожна відповідь у рівнянні вище невід'ємна. Таким чином,

$\sqrt{16}\sqrt{x^6}\sqrt{3} = 4|x^3|\sqrt{3}$

Деякі зауваження по порядку.

• Невід'ємний квадратний корінь з 16 дорівнює 4. Тобто,$\sqrt{16} = 4$
• Невід'ємний квадратний корінь x6 складніший. Некоректно говорити$\sqrt{x^6} = x^3$, тому що$x^3$ може бути негативним (якщо х негативний). Щоб застрахувати невід'ємний квадратний корінь, у цьому випадку нам потрібно обернути нашу відповідь у стовпчики абсолютних значень. Тобто,$\sqrt{x^6} = |x^3|$.

Ми можемо використовувати Правило продукту для абсолютного значення для запису$|x^3| = |x^2||x|$. Оскільки$x^2$ невід'ємний, абсолютні значення барів є надлишковими і не потрібні. Тобто,$|x^2||x| = x^{2}|x|$. Таким чином, ми можемо трохи спростити наше рішення і написати

$4|x^3|\sqrt{3} = 4x^{2}|x|\sqrt{3}$

Таким чином,

$\sqrt{48x^6} = 4x^{2}|x|\sqrt{3}$.

Альтернативне рішення. Існує безліч способів, якими ми можемо розмістити радикальне вираження в простій радикальній формі. Ось ще один підхід. Починаючи з кроку вище, де ми спочатку врахували ідеальний квадрат,

$\sqrt{48x^6} = \sqrt{16x^6}\sqrt{3}$

ми могли б написати

$\sqrt{16x^6}\sqrt{3} = \sqrt{(4x^3)^2}\sqrt{3}$.

Тепер пам'ятайте, що невід'ємний квадратний корінь квадрата виразу є абсолютним значенням цього виразу (ми повинні гарантувати невід'ємну відповідь), тому

$\sqrt{(4x^3)^2}\sqrt{3} = |4x^3|\sqrt{3}$.

Однак$|4x^3| = |4||x^3|$ за нашим правилом продукту і$|4||x^3| = 4|x^3|$. Таким чином,

$|4x^3|\sqrt{3} = 4|x^3|\sqrt{3}$.

Нарешті,$|x^3| = |x^2||x| = x^2|x|$ тому що$x^2 \ge 0$, щоб ми могли написати

$4|x^3|\sqrt{3} = 4x^{2}|x|\sqrt{3}$

Ми не можемо видалити панель абсолютних значень, яка оточує x, якщо ми не знаємо знак х.

Зверніть увагу, що проста радикальна форма в альтернативному розчині ідентична простій радикальній формі, знайденої при попередній техніці рішення.

Давайте розглянемо інший приклад.

Приклад$\PageIndex{14}$

Враховуючи, що x < 0, місце$\sqrt{24x^6}$ в простій радикальній формі.

По-перше, виділіть ідеальний квадрат і напишіть

$\sqrt{24x^6} = \sqrt{4x^6}\sqrt{6}$

Тепер використовуйте Property 1 і візьміть квадратний корінь кожного фактора.

$\sqrt{4x^6}\sqrt{6}= \sqrt{4}\sqrt{x^6}\sqrt{6}$

Щоб застрахувати невід'ємну відповідь$\sqrt{x^6}$, оберніть свою відповідь в абсолютні значення.

$\sqrt{4}\sqrt{x^6}\sqrt{6}=2|x^3|\sqrt{6}$

Однак, як і в попередній проблемі$|x^3| = |x^2||x| = x^{2}|x|$, так як$x^2 \ge 0$. Таким чином,

$2|x^3|\sqrt{6} = 2x^{2}|x|\sqrt{6}$.

У цьому прикладі ми отримали додатковий факт, що x < 0, тому |x| = −x і ми можемо записати

$2x^{2}|x|\sqrt{6} = 2x^{2}(−x)\sqrt{6} = −2x^{3}\sqrt{6}$.

Повчально перевірити достовірність відповіді

$\sqrt{24x^6} = −2x^{3}\sqrt{6}$, x<0.

за допомогою калькулятора.

Малюнок 8. Точкова перевірка дійсності$\sqrt{24x^6} = −2x^{3}\sqrt{6}$.

Дещо контрінтуїтивно, що результат

$\sqrt{24x^6} = −2x^{3}\sqrt{6}$, x<0.

містить негативний знак. Адже вираз$\sqrt{24x^6}$ закликає до ненегативного результату, але у нас є негативний знак. Однак при найближчому розгляді, якщо x < 0, то x є від'ємним числом, а праворуч$−2x^{3}\sqrt{6}$ - додатним числом (−2$x^3$ від'ємний, оскільки x від'ємний, а добуток двох негативів - позитивний).

Давайте розглянемо інший приклад.

Приклад$\PageIndex{15}$

Якщо x < 3, спростити$\sqrt{x^2−6x+9}$.

Вираз під радикалом - це ідеальний квадратний триноміал і фактори.

$\sqrt{x^2−6x+9}=\sqrt{(x−3​​)^2}$

Однак невід'ємний квадратний корінь квадрата виразу є абсолютним значенням цього виразу, тому

$\sqrt{(x−3)^2} =|x−3|$.

Нарешті, тому що нам кажуть, що x < 3, це робить x − 3 від'ємним числом, тому

|x−3| = − (x−3).

Знову ж таки$\sqrt{x^2−6x+9} = −(x−3)$, результат, за умови x < 3, дещо суперечливий, оскільки ми очікуємо позитивного результату. Однак, якщо x < 3, результат − (x−3) буде позитивним. Ви можете перевірити це, підставивши декілька значень x, які менше 3, у вираз − (x−3) і зауваживши, що результат позитивний. Наприклад, якщо x = 2, то x менше 3 і

− (x−3) = − (2−3) = − (−1) = 1,

що, безумовно, є позитивним результатом.

Ще більш інформативно відзначити, що наш результат еквівалентний

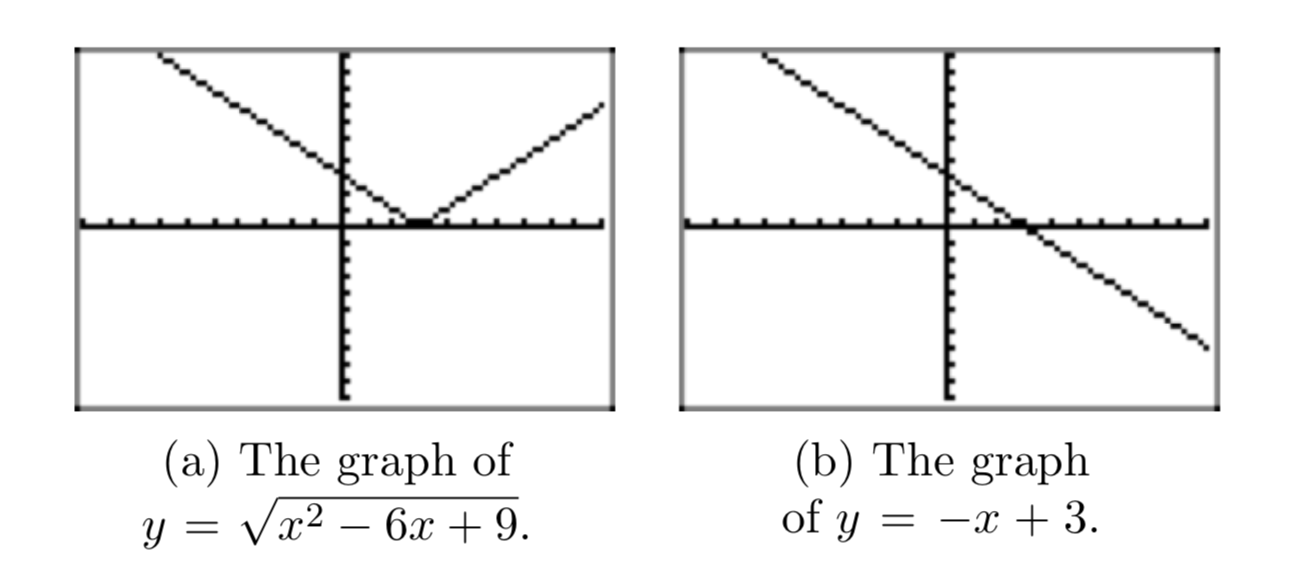
$\sqrt{x^2−6x+9}=−x+3$, х<3.

Це легко побачити, розподіляючи знак мінус у результаті − (x−3).

Ми намалювали графік$y = \sqrt{x^2−6x+9}$ на нашому калькуляторі на малюнку 9 (а). На малюнку 9 (b) ми намалювали графік y = −x + 3. Зверніть увагу, що графіки узгоджуються, коли x < 3. Дійсно, якщо розглядати ліву гілку «V» на малюнку 9 (a), можна побачити, що нахил цієї гілки дорівнює −1, а y-перехоплення дорівнює 3. Рівняння цієї гілки дорівнює y = −x+3, тому воно узгоджується з графіком y = −x+3 на малюнку 9 (b), коли x менше 3.

Малюнок 9. Перевірка графічно, що$\sqrt{x^2−6x+9}=−x+3$ коли x<3.

Вправа$\PageIndex{1}$

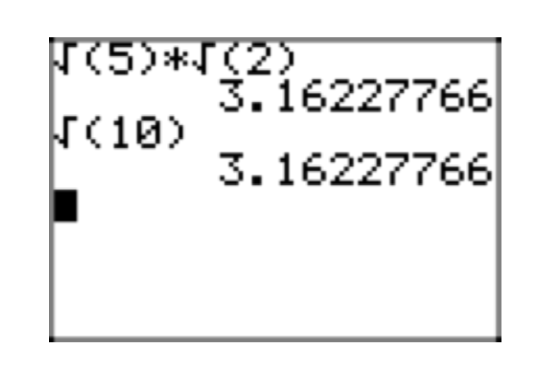
Скористайтеся калькулятором, щоб спочатку наблизити$\sqrt{2}\sqrt{5}$. Один той же екран, приблизний$\sqrt{10}$. Повідомте про результати на домашній папері.

Відповідь

Зауважте, що$\sqrt{5}\sqrt{2} = \sqrt{10} \approx 3.16227766$.

Вправа$\PageIndex{2}$

Скористайтеся калькулятором, щоб спочатку наблизити$\sqrt{7}\sqrt{10}$. Один той же екран, приблизний$\sqrt{70}$. Повідомте про результати на домашній папері.

Вправа$\PageIndex{3}$

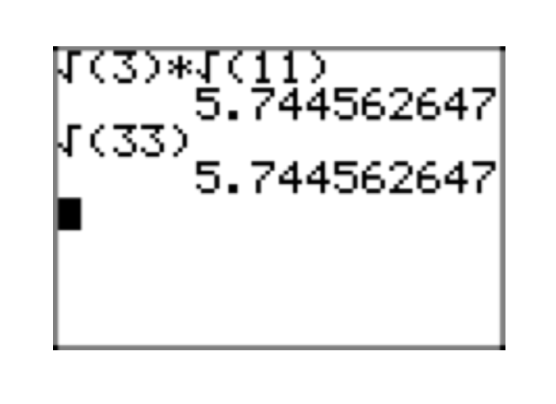
Скористайтеся калькулятором, щоб спочатку наблизити$\sqrt{3}\sqrt{11}$. Один той же екран, приблизний$\sqrt{33}$. Повідомте про результати на домашній папері.

Відповідь

Зауважте, що$\sqrt{3}\sqrt{11} = \sqrt{33} \approx 5.744562647$

Вправа$\PageIndex{4}$

Скористайтеся калькулятором, щоб спочатку наблизити$\sqrt{5}\sqrt{13}$. Один той же екран, приблизний$\sqrt{65}$. Повідомте про результати на домашній папері.

У вправах 5 - 20 помістіть кожне з радикальних виразів в простій радикальній формі. Як і в прикладі 3 в оповіданні, перевірте свій результат за допомогою калькулятора.

Вправа$\PageIndex{5}$

$\sqrt{18}$

Відповідь

$\sqrt{18} = \sqrt{3^{2} \cdot 2}= \sqrt{3^{2}}\sqrt{2}=3\sqrt{2}$

Вправа$\PageIndex{6}$

$\sqrt{80}$

Вправа$\PageIndex{7}$

$\sqrt{112}$

Відповідь

$\sqrt{112} = \sqrt{4^{2} \cdot 7}= \sqrt{4^{2}}\sqrt{7}=4\sqrt{7}$

Вправа$\PageIndex{8}$

$\sqrt{72}$

Вправа$\PageIndex{9}$

$\sqrt{108}$

Відповідь

$\sqrt{108} = \sqrt{6^{2} \cdot 3}= \sqrt{6^{2}}\sqrt{3}=6\sqrt{3}$

Вправа$\PageIndex{10}$

$\sqrt{54}$

Вправа$\PageIndex{11}$

$\sqrt{50}$

Відповідь

$\sqrt{50} = \sqrt{5^{2} \cdot 2}= \sqrt{5^{2}}\sqrt{2}=5\sqrt{2}$

Вправа$\PageIndex{12}$

$\sqrt{48}$

Вправа$\PageIndex{13}$

$\sqrt{245}$

Відповідь

$\sqrt{245} = \sqrt{7^{2} \cdot 5}= \sqrt{7^{2}}\sqrt{5}=7\sqrt{5}$

Вправа$\PageIndex{14}$

$\sqrt{150}$

Вправа$\PageIndex{15}$

$\sqrt{98}$

Відповідь

$\sqrt{98} = \sqrt{7^{2} \cdot 2}= \sqrt{7^{2}}\sqrt{2}=7\sqrt{2}$

Вправа$\PageIndex{16}$

$\sqrt{252}$

Вправа$\PageIndex{17}$

$\sqrt{45}$

Відповідь

$\sqrt{45} = \sqrt{3^{2} \cdot 5}= \sqrt{3^{2}}\sqrt{5}=3\sqrt{5}$

Вправа$\PageIndex{18}$

$\sqrt{294}$

Вправа$\PageIndex{19}$

$\sqrt{24}$

Відповідь

$\sqrt{24} = \sqrt{2^{2} \cdot 6}= \sqrt{2^{2}}\sqrt{6}=2\sqrt{6}$

Вправа$\PageIndex{20}$

$\sqrt{32}$

У вправах 21 - 26 використовуйте просту факторизацію (як у прикладі 10 та 11 в оповіданні), щоб допомогти вам розмістити даний радикальний вираз у простій радикальній формі. C Перевірте свій результат за допомогою калькулятора.

Вправа$\PageIndex{21}$

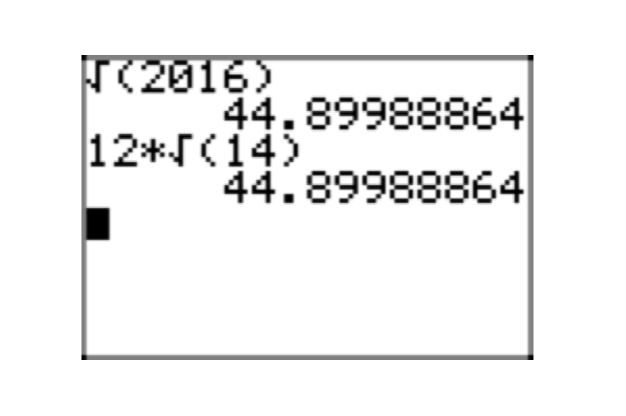
$\sqrt{2016}$

Відповідь

Зверніть увагу, що 2+0+1+6 = 9, що ділиться на 9. Таким чином, 2016 рік ділиться на 9. Дійсно,

$2019 = 9 \cdot 224$

Останні дві цифри 224 - це 24, що ділиться на 4. Таким чином, 224 ділиться на 4. Дійсно,$224 = 4 \cdot 56$.

$2016 = 9 \cdot 224 = (3 \cdot 3) \cdot (4 \cdot 56)$.

Продовжуйте до простих чисел.

$2016=3 \cdot 3 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 7 = 2^{5} \cdot 3^{2} \cdot 7$.

Перевірка,

Вправа$\PageIndex{22}$

$\sqrt{2700}$

Вправа$\PageIndex{23}$

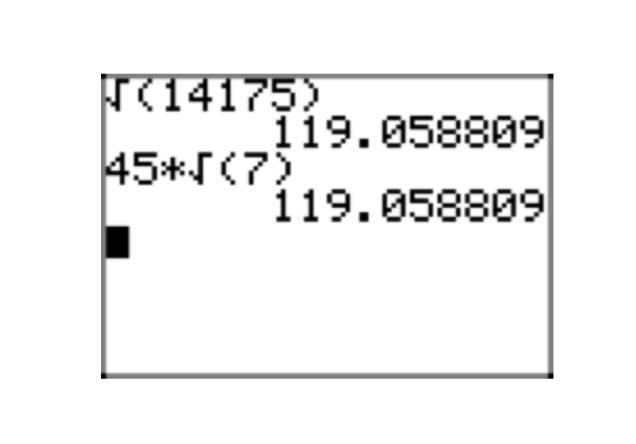
$\sqrt{14175}$

Відповідь

Гроші! Все, що закінчується на 00, 25, 50 або 75, ділиться на 25. Дійсно,$14175 = 25 \cdot 567$. Далі 5+6+7 = 18, тому 567 ділиться на 9; т$567 = 9 \cdot 63$. Е. Продовжуючи до простих чисел,

$14175 = 25 \cdot 567 = 5 \cdot 5 \cdot 9 \cdot 63 = 5 \cdot 5 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 7$.

Фактор наш ідеальний квадрат (експоненти ділиться на 2).

\(\sqrt{14175} = \sqrt{3^{4} \cdot 5^{2}} \cdot \sqrt{7} = 3^{2} \cdot 5\sqrt{7} = 45\sqrt{7}\)

Перевірка,

Вправа$\PageIndex{24}$

$\sqrt{44000}$

Вправа$\PageIndex{25}$

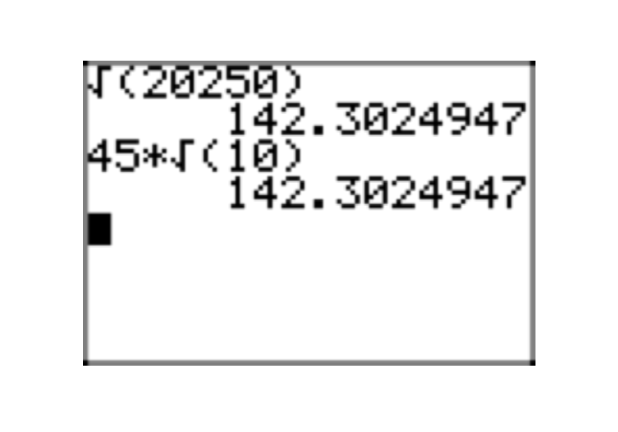
$\sqrt{20250}$

Відповідь

Гроші! Все, що закінчується на 00, 25, 50 або 75, ділиться на 25. Дійсно,$20250 = 25 \cdot 810$. Продовжуючи до простих чисел,

$20250 = 5 \cdot 5 \cdot 9 \cdot 9 \cdot 10 = 5 \cdot 5 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 2 \cdot 5$.

Фактор з ідеального квадрата.

$\sqrt{20250} = \sqrt{2 \cdot 3^{4} \cdot 5^{3}} = \sqrt{3^{4} \cdot 5^{2}} \cdot \sqrt{2 \cdot 5} = 3^{2} \cdot 5 \sqrt{2 \cdot 5}=45\sqrt{10}$

Перевірка,

Вправа$\PageIndex{26}$

$\sqrt{3564}$

У вправах 27 - 46 помістіть кожне з заданих радикальних виразів в простій радикальній формі. Не робіть припущень про знак змінних. Змінні можуть представляти позитивні або від'ємні числа.

Вправа$\PageIndex{27}$

$\sqrt{(6x−11)^4}$

Відповідь

$\sqrt{(6x−11)^4} = \sqrt{((6x−11)^2)^2} = |(6x−11)^2|$

Однак$(6x − 11)^2$ це вже невід'ємний, тому бари абсолютних значень непотрібні. Отже,

$\sqrt{(6x−11)^4} = (6x−11)^2$

Вправа$\PageIndex{28}$

$\sqrt{16h^8}$

Вправа$\PageIndex{29}$

$\sqrt{25f^2}$

Відповідь

$\sqrt{25f^2} = \sqrt{25}\sqrt{f^2} = 5|f|$

Оскільки f може бути будь-яким дійсним числом, ми не можемо видалити бари абсолютних значень без додаткової інформації.

Вправа$\PageIndex{30}$

$\sqrt{25j^8}$

Вправа$\PageIndex{31}$

$\sqrt{16m^2}$

Відповідь

$\sqrt{16m^2} = \sqrt{4^{2}m^2} = \sqrt{4^2}\sqrt{m^2} = 4|m|$

Так як індекс на радикалі парний і після спрощення змінна підвищується до непарної потужності, необхідні знаки абсолютного значення навколо спрощеної змінної.

Вправа$\PageIndex{32}$

$\sqrt{25a^2}$

Вправа$\PageIndex{33}$

$\sqrt{(7x+5)^{12}}$

Відповідь

$\sqrt{(7x+5)^{12}} = \sqrt{((7x+5)^6)^2} = |(7x+5)^6|$

Однак вже$(7x+5)^6$ невід'ємний, тому абсолютні значення знаків не потрібні.

$\sqrt{(7x+5)^{12}} = (7x+5)^6$

Вправа$\PageIndex{34}$

$\sqrt{9w^{10}}$

Вправа$\PageIndex{35}$

$\sqrt{25x^2−50x+25}$

Відповідь

$\sqrt{25x^2−50x+25}=\sqrt{(5x−5)^2} =|5x−5|$

Оскільки x може бути будь-яким дійсним числом, необхідні знаки абсолютного значення навколо спрощеного біноміалу.

Вправа$\PageIndex{36}$

$\sqrt{49x^2−42x+9}$

Вправа$\PageIndex{37}$

$\sqrt{25x^2+90x+81}$

Відповідь

$\sqrt{25x^2+90x+81} = \sqrt{(5x+9)^2} = |5x+9|$

Оскільки x може бути будь-яким дійсним числом, необхідні знаки абсолютного значення навколо спрощеного біноміалу.

Вправа$\PageIndex{38}$

$\sqrt{25f^{14}}$

Вправа$\PageIndex{39}$

$\sqrt{(3x+6)^{12}}$

Відповідь

$\sqrt{(3x+6)^{12}} = \sqrt{((3x+6)^6)^2} = |(3x+6)^6|$

Однак вираз вже$(3x+6)^6$ невід'ємний, тому бари абсолютних значень непотрібні.

$\sqrt{(3x+6)^{12}} = (3x+6)^6$

Вправа$\PageIndex{40}$

$\sqrt{(9x−8)^{12}}$

Вправа$\PageIndex{41}$

$\sqrt{36x^2+36x+9}$

Відповідь

$\sqrt{36x^2+36x+9} = \sqrt{(6x+3)^2} =|6x+3|$

Оскільки x може бути будь-яким дійсним числом, необхідні знаки абсолютного значення навколо спрощеного біноміалу.

Вправа$\PageIndex{42}$

$\sqrt{4e^2}$

Вправа$\PageIndex{43}$

$\sqrt{4p^{10}}$

Відповідь

$\sqrt{4p^{10}} = \sqrt{4}\sqrt{(p^5)^2}=2|p^5|$

Тепер ми можемо використовувати мультиплікативну властивість абсолютних значень і записати

$2|p^5| = 2|p^4||p| = 2p^{4}|p|$.

Оскільки p може бути будь-яким дійсним числом, необхідні знаки абсолютного значення навколо спрощеної змінної.

Вправа$\PageIndex{44}$

$\sqrt{25x^{12}}$

Вправа$\PageIndex{45}$

$\sqrt{25q^6}$

Відповідь

$\sqrt{25q^6} = \sqrt{25}\sqrt{(q^3)^2} = 5|q^3|$

Тепер ми можемо використовувати мультиплікативну властивість абсолютних значень і записати

$5|q^3| = 5|q^2||q| = 5q^{2}|q|$.

Оскільки q може бути будь-яким дійсним числом, необхідні знаки абсолютного значення навколо спрощеної змінної.

Вправа$\PageIndex{46}$

$\sqrt{16h^{12}}$

Вправа$\PageIndex{47}$

Враховуючи, що x < 0, помістіть радикальний вираз$\sqrt{32x^6}$ у простій радикальній формі. Перевірте рішення у вашому калькуляторі для x = −2.

Відповідь

Фактор з ідеального квадрата.

$\sqrt{32x^6} = \sqrt{16x^6}\sqrt{2} = \sqrt{16}\sqrt{x^6}\sqrt{2}=4|x^3|\sqrt{2}$

Однак$|x^3| = |x^2||x| = x^2|x|$, так як$x^2 \ge 0$. Таким чином

$\sqrt{32x^6} = 4x^{2}|x|\sqrt{2}$.

Якщо x < 0, то |x| = −x і

$\sqrt{32x^6} = 4x^{2}(−x)\sqrt{2} =−4x^{3}\sqrt{2}$.

Перевірка за допомогою x = − 2.

Вправа$\PageIndex{48}$

Враховуючи, що x < 0, помістіть радикальний вираз$\sqrt{54x^8}$ у простій радикальній формі. Перевірте рішення у вашому калькуляторі для x = −2.

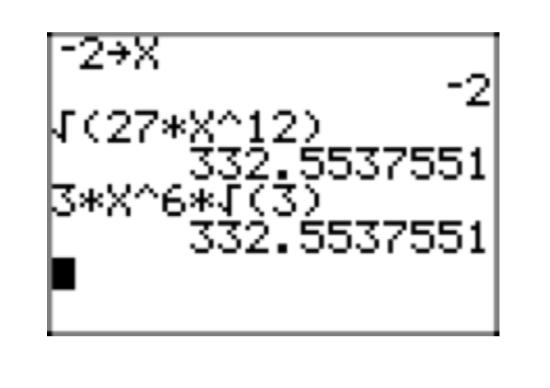
Вправа$\PageIndex{49}$

Враховуючи, що x < 0, помістіть радикальний вираз$\sqrt{27x^{12}}$ у простій радикальній формі. Перевірте рішення у вашому калькуляторі для x = −2.

Відповідь

Фактор з ідеального квадрата.

$\sqrt{27x^{12}} = \sqrt{9x^{12}}\sqrt{3} = \sqrt{9}\sqrt{x^{12}}\sqrt{3}=3|x^6|\sqrt{3}$

Однак,$|x^6| = x^6$ так як$x^6 \ge 0$. Таким чином,

$\sqrt{27x^{12}}=3x^{6}\sqrt{3}$

Перевірка за допомогою x = − 2.

Вправа$\PageIndex{50}$

Враховуючи, що x < 0, помістіть радикальний вираз$\sqrt{44x^{10}}$ у простій радикальній формі. Перевірте рішення у вашому калькуляторі для x = −2.

У Вправи 51 - 54 дотримуйтесь наведення Прикладу 17 в оповіданні, щоб спростити даний радикальний вираз і перевірити свій результат за допомогою графічного калькулятора.

Вправа$\PageIndex{51}$

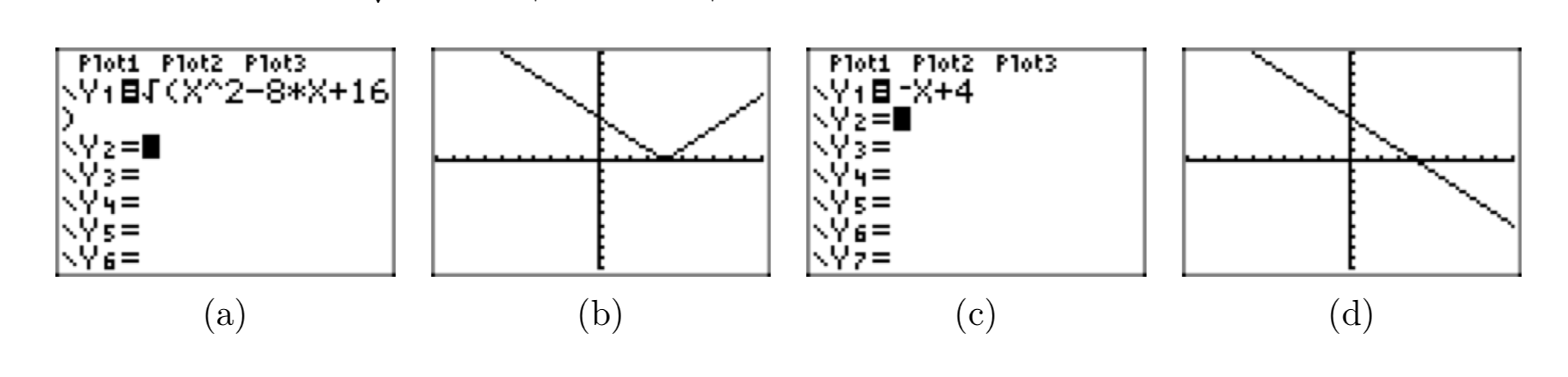
Враховуючи, що x < 4, помістіть радикальний вираз$\sqrt{x^2−8x+16}$ в простій радикальній формі. Скористайтеся графічним калькулятором, щоб показати, що графіки вихідного виразу та вашої простої радикальної форми узгоджуються для всіх значень x, таких як x < 4.

Відповідь

Фактор ідеальний квадратний триноміал.

$\sqrt{x^2−8x+16} = \sqrt{(x−4)^2} =|x−4|$

Якщо x < 4, або еквівалентно, якщо x−4 < 0, то |x−4| = − (x−4). Таким чином,

$\sqrt{x^2−8x+16} =−x+4$.

У (b) ми намалювали графік$y = \sqrt{x^2−8x+16}$. У (d) ми намалювали графік y = −x+4. Зверніть увагу, що графіки в (b) і (d) згодні, коли x < 4, що веде до того, що$\sqrt{x^2−8x+16} =−x+4$ при x < 4.

Вправа$\PageIndex{52}$

Враховуючи це$x \ge −2$, помістіть радикальний вираз$\sqrt{x^2+4x+4}$ в простій радикальній формі. Використовуйте графічний калькулятор, щоб показати, що графіки вихідного виразу та вашої простої радикальної форми узгоджуються для всіх значень x, таких як$x \ge −2$.

Вправа$\PageIndex{53}$

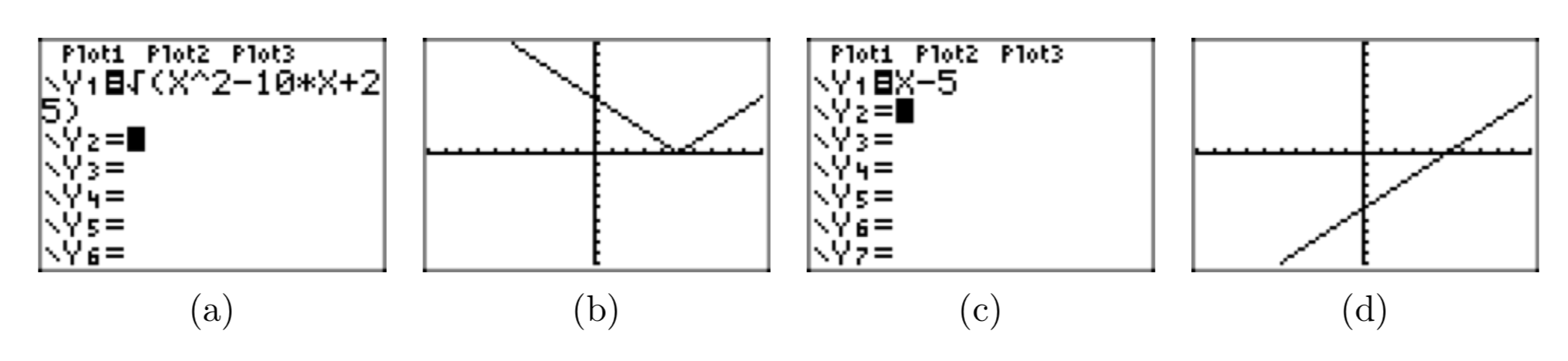
Враховуючи це$x \ge 5$, помістіть радикальний вираз$\sqrt{x^2−10x+25}$ в простій радикальній формі. Використовуйте графічний калькулятор, щоб показати, що графіки вихідного виразу та вашої простої радикальної форми узгоджуються для всіх значень x, таких як$x \ge 5$.

Відповідь

Фактор ідеальний квадратний триноміал.

$\sqrt{x^2−10x+25} = \sqrt{(x−5)^2} =|x−5|$

Якщо$x \ge 5$, або еквівалентно, if$x−5 \ge 0$, то |x−5| = x−5. Таким чином,

$\sqrt{x^2−8x+16} =x−5$.

У (b) ми намалювали графік$y = \sqrt{x^2−10x+25}$. У (d) ми намалювали графік y = x−5. Зверніть увагу, що графіки в (b) і (d) погоджуються$x \ge 5$, коли, ведучи довіру до того, що$\sqrt{x^2−10x+25} = x−5$ коли$x \ge 5$.

Вправа$\PageIndex{54}$

Враховуючи, що x < −1, помістіть радикальний вираз$\sqrt{x^2+2x+1}$ у простій радикальній формі. Скористайтеся графічним калькулятором, щоб показати, що графіки вихідного виразу та вашої простої радикальної форми узгоджуються для всіх значень x, таких як x < −1.

У вправах 55 - 72 помістіть кожне радикальне вираз в просту радикальну форму. Припустимо, що всі змінні представляють собою позитивні числа.

Вправа$\PageIndex{55}$

$\sqrt{9d^{13}}$

Відповідь

$\sqrt{9d^{13}} = \sqrt{9}\sqrt{d^{12}}\sqrt{d}=3d^6\sqrt{d}$

Вправа$\PageIndex{56}$

$\sqrt{4k^2}$

Вправа$\PageIndex{57}$

$\sqrt{25x^2+40x+16}$

Відповідь

$\sqrt{25x^2+40x+16} = \sqrt{(5x+4)^2} = 5x+4$

Вправа$\PageIndex{58}$

$\sqrt{9x^2−30x+25}$

Вправа$\PageIndex{59}$

$\sqrt{4j^{11}}$

Відповідь

$\sqrt{4j^{11}} = \sqrt{4}\sqrt{j^{10}}\sqrt{j}=3j^5\sqrt{j}$

Вправа$\PageIndex{60}$

$\sqrt{16j^6}$

Вправа$\PageIndex{61}$

$\sqrt{25m^2}$

Відповідь

$\sqrt{25m^2} = \sqrt{25}\sqrt{m^2} = 5m$

Вправа$\PageIndex{62}$

$\sqrt{9e^9}$

Вправа$\PageIndex{63}$

$\sqrt{4c^5}$

Відповідь

$\sqrt{4c^5} = \sqrt{4c^4}\sqrt{c} = 2c^{2}\sqrt{c}$

Вправа$\PageIndex{64}$

$\sqrt{25z^2}$

Вправа$\PageIndex{65}$

$\sqrt{25h^{10}}$

Відповідь

$\sqrt{25h^{10}} = \sqrt{25}\sqrt{h^{10}} = 5h^5$

Вправа$\PageIndex{66}$

$\sqrt{25b^2}$

Вправа$\PageIndex{67}$

$\sqrt{9s^7}$

Відповідь

$\sqrt{9s^7} = \sqrt{9s^6}\sqrt{s} = 3s^{3}\sqrt{s}$

Вправа$\PageIndex{68}$

$\sqrt{9e^7}$

Вправа$\PageIndex{69}$

$\sqrt{4p^8}$

Відповідь

$\sqrt{4p^8} = \sqrt{4}\sqrt{p^8} = 2\sqrt{p^4}$

Вправа$\PageIndex{70}$

$\sqrt{9d^{15}}$

Вправа$\PageIndex{71}$

$\sqrt{9q^{10}}$

Відповідь

$\sqrt{9q^{10}} = \sqrt{9}\sqrt{q^{10}} = 3\sqrt{q^5}$

Вправа$\PageIndex{72}$

$\sqrt{4w^7}$

У вправах 73 - 80 помістіть кожне задане радикальне вираження в простій радикальній формі. Припустимо, що всі змінні представляють собою позитивні числа.

Вправа$\PageIndex{73}$

$\sqrt{2f^5}\sqrt{8f^3}$

Відповідь

$\sqrt{2f^5}\sqrt{8f^3} =\sqrt{2 \cdot 8 \cdot f^5 \cdot f^3} = \sqrt{16f^8} = \sqrt{16}\sqrt{(f^4)^2} =4f^4$

Вправа$\PageIndex{74}$

$\sqrt{3s^3}\sqrt{243s^3}$

Вправа$\PageIndex{75}$

$\sqrt{2k^7}\sqrt{32k^3}$

Відповідь

$\sqrt{2k^7}\sqrt{32k^3} = \sqrt{2 \cdot 32 \cdot k^7 \cdot k^3} = \sqrt{64k^{10}} = \sqrt{64}\sqrt{(k^5)^2}=8k^5$

Вправа$\PageIndex{76}$

$\sqrt{2n^9}\sqrt{8n^3}$

Вправа$\PageIndex{77}$

$\sqrt{2e^9}\sqrt{8e^3}$

Відповідь

$\sqrt{2e^9}\sqrt{8e^3} = \sqrt{2 \cdot 8 \cdot e^9 \cdot e^3} = \sqrt{16e^{12}} = \sqrt{16}\sqrt{(e^6)^2}=4e^6$

Вправа$\PageIndex{78}$

$\sqrt{5n^9}\sqrt{125n^3}$

Вправа$\PageIndex{79}$

$\sqrt{3z^5}\sqrt{27z^3}$

Відповідь

$\sqrt{3z^5}\sqrt{27z^3} = \sqrt{3 \cdot 27 \cdot z^5 \cdot z^3} = \sqrt{81z^8} = \sqrt{81}\sqrt{(z^4)^2}=9z^4$

Вправа$\PageIndex{80}$

$\sqrt{3t^7}\sqrt{27t^3}$