8.2: Спрощення радикальних виразів

Last updated
Save as PDF

Page ID: 58256

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Почнемо з порівняння двох математичних виразів.

\[\begin{align*} \sqrt{9}\sqrt{16} &= 3\cdot 4 \\ &= 12 \end{align*} \nonumber \]

\[\begin{align*} \sqrt{9\cdot 16} &= \sqrt{144} \\ &= 12 \end{align*} \nonumber\]

Зверніть увагу, що обидва$\sqrt{9}\sqrt{16}$ і$\sqrt{9\cdot 16}$ рівні$12$. Отже,$\sqrt{9}\sqrt{16} = \sqrt{9\cdot 16}$. Давайте розглянемо інший приклад.

\[\begin{align*} \sqrt{4}\sqrt{9} &= 2\cdot 3 \\ &= 6 \end{align*} \nonumber \]

\[\begin{align*} \sqrt{4\cdot 9} &= \sqrt{36} \\ &= 6 \end{align*} \nonumber\]

Зверніть увагу, що обидва$\sqrt{4}\sqrt{9}$ і$\sqrt{4\cdot 9}$ рівні$6$. Отже,$\sqrt{4}\sqrt{9} = \sqrt{4\cdot 9}$. Виявляється, що формується візерунок, а саме:

\[\sqrt{a}\sqrt{b} = \sqrt{ab} \nonumber \]

Спробуємо приклад на нашому калькуляторі. Спочатку введіть$\sqrt{2}\sqrt{3}$, потім введіть$\sqrt{2\cdot 3}$ (див. Рис.$\PageIndex{1}$). Зверніть увагу, що вони дають однаковий результат. Тому,$\sqrt{2}\sqrt{3} = \sqrt{2\cdot 3}$

рис. 8.2.1.png — Малюнок$\PageIndex{1}$: Зверніть увагу, що$\sqrt{2}\sqrt{3} = \sqrt{2\cdot 3}$

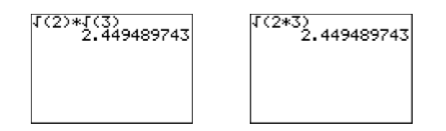
Вищевикладене обговорення призводить нас до наступного результату.

Властивість множення радикалів

Якщо$a ≥ 0$ і$b ≥ 0$, то:\[\sqrt{a}\sqrt{b} = \sqrt{a\cdot b} \nonumber \]

Приклад$\PageIndex{1}$

Максимально спростіть кожне з наступних виразів:

$\sqrt{3} \sqrt{11}$
$\sqrt{12} \sqrt{3}$
$\sqrt{2} \sqrt{13}$

Рішення

У кожному конкретному випадку використовуйте властивість$\sqrt{a} \sqrt{b}=\sqrt{a b}$. Тобто помножте два числа під знаком квадратного кореня, помістивши твір під єдиним квадратним коренем.

$\begin{aligned} \sqrt{3} \sqrt{11} &=\sqrt{3 \cdot 11} \\ &=\sqrt{33} \end{aligned}$
$\begin{aligned} \sqrt{12} \sqrt{3} &=\sqrt{12 \cdot 3} \\ &=\sqrt{36} \\ &=6 \end{aligned}$
$\begin{aligned} \sqrt{2} \sqrt{13} &=\sqrt{2 \cdot 13} \\ &=\sqrt{26} \end{aligned}$

Вправа$\PageIndex{1}$

Спростити:$\sqrt{2} \sqrt{8}$

Відповідь: $4$

Проста радикальна форма

Ми також можемо використовувати властивість$\sqrt{a} \sqrt{b}=\sqrt{a b}$ у зворотному напрямку, щоб врахувати ідеальний квадрат. Наприклад:

\[\begin{array}{rlrl}{\sqrt{50}} & {=\sqrt{25} \sqrt{2}} & {} & \color {Red} {\text { Factor out a perfect square. }} \\ {} & {=5 \sqrt{2}} & {} & \color {Red} {\text { Simplify: } \sqrt{25}=5}\end{array} \nonumber \]

Кажуть,$5\sqrt{2}$ що вираз знаходиться в простій радикальній формі. Як і зменшення дробу до найнижчих показників, ви завжди повинні враховувати ідеальний квадрат, коли це можливо.

Проста радикальна форма

Якщо можливо, завжди враховуйте ідеальний квадрат.

Приклад$\PageIndex{2}$

Місце$\sqrt{8}$ в простій радикальній формі.

Рішення

З$\sqrt{8}$, ми можемо врахувати ідеальний квадрат, в даному випадку$\sqrt{4}$.

\[\begin{array}{rlrl}{\sqrt{8}} & {=\sqrt{4} \sqrt{2}} & {} & \color {Red} {\text { Factor out a perfect square. }} \\ {} & {=2 \sqrt{2}} & {} & \color {Red} {\text { Simplify: } \sqrt{4}=2}\end{array} \nonumber \]

Вправа$\PageIndex{2}$

Місце$\sqrt{12}$ в простій радикальній формі.

Відповідь: $2\sqrt{3}$

Іноді, після факторингу ідеального квадрата, ви все одно можете зарахувати ще один ідеальний квадрат.

Приклад$\PageIndex{3}$

Місце$\sqrt{72}$ в простій радикальній формі.

Рішення

З$\sqrt{72}$, ми можемо врахувати ідеальний квадрат, в даному випадку$\sqrt{9}$.

\[\begin{array}{rlrl}{\sqrt{72}} & {=\sqrt{9} \sqrt{8}} & {} & \color {Red} {\text { Factor out a perfect square. }} \\ {} & {=3 \sqrt{8}} & {} & \color {Red} {\text { Simplify: } \sqrt{9}=3}\end{array} \nonumber \]

Однак у цьому випадку$\sqrt{8}$ ми можемо врахувати ще один ідеальний квадрат$\sqrt{4}$.

\[\begin{array}{ll}{=3 \sqrt{4} \sqrt{2}} & \color {Red} {\text { Factor out another perfect square. }} \\ {=3 \cdot 2 \cdot \sqrt{2}} & \color {Red} {\text { Simplify: } \sqrt{4}=2} \\ {=6 \sqrt{2}} & \color {Red} {\text { Multiply: } 3 \cdot 2=6}\end{array} \nonumber \]

Альтернативне рішення

Ми можемо спростити процес, зазначивши, що ми можемо$\sqrt{36}$ враховувати$\sqrt{72}$, щоб почати процес.

\[\begin{array}{rlrl}{\sqrt{72}} & {=\sqrt{36} \sqrt{2}} & {} & \color {Red} {\text { Factor out a perfect square. }} \\ {} & {=6 \sqrt{2}} & {} & \color {Red} {\text { Simplify: } \sqrt{36}=6}\end{array} \nonumber \]

Хоча друге рішення є більш ефективним, перше рішення все одно математично правильне. Справа тут полягає в тому, що ми повинні продовжувати враховувати ідеальний квадрат, коли це можливо. Наша відповідь не в простій радикальній формі, поки ми більше не зможемо зарахувати ідеальний квадрат.

Вправа$\PageIndex{3}$

Місце$\sqrt{200}$ в простій радикальній формі.

Відповідь: $10\sqrt{2}$

Теорема Піфагора

Кут, який вимірює$90$ градуси, називається прямим кутом. Якщо один з кутів трикутника - прямий кут, то трикутник називається прямокутним. Традиційно розмічати прямий кут невеликим квадратом (див. Рис.$\PageIndex{2}$).

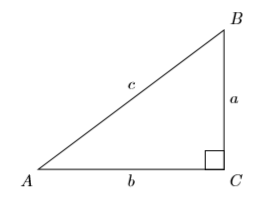
рис. 8.2.2.png — Малюнок$\PageIndex{2}$: Прямокутний трикутник$\triangle A B C$ має прямий кут у вершині$C$.

Термінологія правого трикутника

Найдовша сторона прямокутного трикутника, сторона прямо протилежна прямому куту, називається гіпотенузою прямокутного трикутника.
Решта дві сторони прямокутного трикутника називаються ніжками прямокутного трикутника.

Доказ теореми Піфагора

Кожна сторона квадрата на малюнку$\PageIndex{3}$ була розділена на два відрізки$a$, один довжиною, інший довжини$b$.

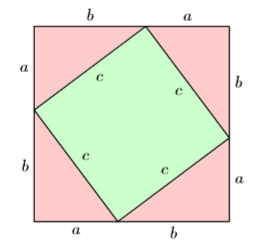
рис. 8.2.3.png — Малюнок$\PageIndex{3}$: Доведення теореми Піфагора.

Ми можемо знайти загальну площу квадрата за допомогою квадрата будь-якої із сторін квадрата.

\[\begin{array}{ll}{A=(a+b)^{2}} & \color {Red} {\text { Square a side to find area. }} \\ {A=a^{2}+2 a b+b^{2}} & \color {Red} {\text { Squaring a binomial pattern. }}\end{array} \nonumber\]

Таким чином, загальна площа площі дорівнює$A = a^2 +2ab + b^2$.

Другий підхід до пошуку площі квадрата полягає в тому, щоб підсумувати площі геометричних частин, що складають квадрат. У нас є чотири конгруентні прямокутні трикутники, затінені світло-червоним кольором, з основою$a$ та висотою$b$. Площа кожного з цих трикутників знаходить, взявши в півтора рази підставу на висоту; тобто площа кожного трикутника дорівнює$(1 / 2) a b$. В інтер'єрі ми маємо менший квадрат зі стороною$c$. Його площа знаходиться шляхом квадратизації його боку; тобто площа меншого квадрата є$c^2$.

Загальна площа квадрата - це сума його частин, одного меншого квадрата і чотирьох конгруентних трикутників. Тобто:

\[\begin{array}{ll}{A=c^{2}+4\left(\frac{1}{2} a b\right)} & \color {Red} {\text { Adding the area of the interior square and the area of four right triangles. }} \\ {A=c^{2}+2 a b} & \color {Red} {\text { Simplify: } 4((1 / 2) a b)=2 a b}\end{array} \nonumber \]

Два вирази,$a^2 +2ab+ b^2$ і$c^2 +2ab$, обидва представляють загальну площу великого квадрата. Значить, вони повинні дорівнювати один одному.

\[\begin{aligned} a^{2}+2 a b+b^{2}=c^{2}+2 a b & \quad \color {Red} \text { Each side of this equation represents the area of the large square. } \\ a^{2}+b^{2}=c^{2} & \quad \color {Red} \text { Subtract } 2 a b \text { from both sides. } \end{aligned} \nonumber \]

Останнє рівняння$a^2 + b^2 = c^2$, називається теоремою Піфагора.

Теорема Піфагора

Якщо$a$ і$b$ є катетами прямокутного трикутника і$c$ є його гіпотенузою, то:

\[a^2 + b^2 = c^2 \nonumber \]

Ми говоримо «Сума квадратів катетів прямокутного трикутника дорівнює квадрату його гіпотенузи».

Хороша підказка: Зверніть увагу, що гіпотенуза сидить сама по собі на одній стороні рівняння$a^2 + b^2 = c^2$. Ніжки гіпотенузи знаходяться з іншого боку.

Давайте поставимо теорему Піфагора на роботу.

Приклад$\PageIndex{4}$

Знайдіть довжину відсутньої сторони прямокутного трикутника, показану нижче.

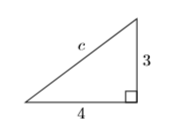
$рис. 8.2.4.png$

Рішення

Спочатку випишіть теорему Піфагора, потім підставляйте задані значення у відповідні місця.

\[\begin{aligned} a^{2}+b^{2}=c^{2} & \color {Red} \text { Pythagorean Theorem. } \\(4)^{2}+(3)^{2}=c^{2} & \color {Red} \text { Substitute: } 4 \text { for } a, 3 \text { for } b \\ 16+9=c^{2} & \color {Red} \text { Square: }(4)^{2}=16,(3)^{2}=9 \\ 25=c^{2} & \color {Red} \text { Add: } 16+9=25 \end{aligned} \nonumber \]

Рівняння$c^2 = 25$ має два реальних рішення,$c = −5$ і$c = 5$. Однак в цій ситуації$c$ являє собою довжину гіпотенузи і має бути позитивним числом. Звідси:

\[c=5 \quad \color {Red} \text { Nonnegative square root. } \nonumber \]

Таким чином, довжина гіпотенузи дорівнює$5$.

Вправа$\PageIndex{4}$

Знайдіть відсутню сторону прямокутного трикутника, показану нижче.

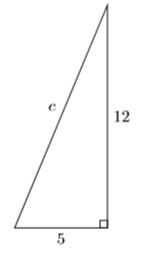
$Колишній 8.2.4.png$

Відповідь: $13$

Приклад$\PageIndex{5}$

Рівнобедрений прямокутний трикутник має гіпотенузу довжини$8$. Знайдіть довжини ніжок.

Рішення

Взагалі, рівнобедрений трикутник - це трикутник з двома рівними сторонами. При цьому рівнобедрений прямокутний трикутник має дві рівні ніжки. Ми дозволимо$x$ представляти довжину кожної ноги.

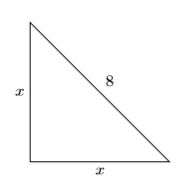
$рис. 8.2.5.png$

Використовуйте теорему Піфагора, підставляючи$x$ для кожного катета і$8$ для гіпотенузи.

\[\begin{array}{rlrl}{a^{2}+b^{2}} & {=c^{2}} & {} & \color {Red} {\text { Pythagorean Theorem. }} \\ {x^{2}+x^{2}} & {=8^{2}} & {} & \color {Red} {\text { Substitute: } x \text { for } a, x \text { for } b, 8 \text { for } c .} \\ {2 x^{2}} & {=64} & {} & \color {Red} {\text { Combine like terms: } x+x=2 x} \\ {x^{2}} & {=32} & {} & \color {Red} {\text { Divide both sides by } 2}\end{array} \nonumber \]

Рівняння$x^2 = 32$ має два реальних рішення,$x=-\sqrt{32}$ і$x=\sqrt{32}$. Однак в цій ситуації,$x$ являє собою довжину кожної ноги і повинна бути позитивним числом. Звідси:

\[x=\sqrt{32} \quad \color {Red} \text { Nonnegative square root. } \nonumber \]

Пам'ятайте, ваша остаточна відповідь повинна бути в простій радикальній формі. Ми повинні враховувати ідеальний квадрат, коли це можливо.

\[\begin{array}{ll}{x=\sqrt{16} \sqrt{2}} & \color {Red} {\text { Factor out a perfect square. }} \\ {x=4 \sqrt{2}} & \color {Red} {\text { Simplify: } \sqrt{16}=4}\end{array} \nonumber \]

Таким чином, довжина кожної ноги дорівнює$4\sqrt{2}$.

Вправа$\PageIndex{5}$

Рівнобедрений прямокутний трикутник має гіпотенузу довжини$10$. Знайдіть довжини ніжок.

Відповідь: Кожна нога має довжину$5\sqrt{2}$

Додатки

Спробуємо проблему зі словом.

Приклад$\PageIndex{6}$

Сходи$20$ ноги довго спираються на стіну гаража. Якщо основа сходів знаходиться в$8$ футах від стіни гаража, наскільки високо до стіни гаража досягає сходи? Знайдіть точну відповідь, а потім скористайтеся калькулятором, щоб округлити відповідь до найближчої десятої частини фута.

Рішення

Як завжди, ми дотримуємося вимог до вирішення проблем Word.

Налаштуйте словник змінних. Створимо для цього добре розмічену схему, дозволяючи$h$ представити відстань між підставою стіни гаража і верхнім кінчиком сходів.

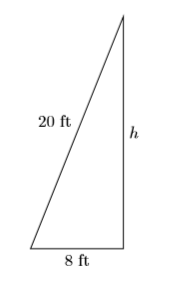
$рис. 8.2.6.png$

Налаштуйте рівняння. Використовуючи теорему Піфагора, ми можемо записати:\[\begin{array}{ll}{8^{2}+h^{2}=20^{2}} & \color {Red} {\text { Pythagorean Theorem. }} \\ {64+h^{2}=400} & \color {Red} {\text { Square: } 8^{2}=64 \text { and } 20^{2}=400}\end{array} \nonumber \]
Розв'яжіть рівняння. \[\begin{array}{ll}{h^{2}=336} & \color {Red} {\text { Subtract } 64 \text { from both sides. }} \\ {h=\sqrt{336}} & \color {Red} {h \text { will be the nonnegative square root. }} \\ {h=\sqrt{16} \sqrt{21}} & \color {Red} {\text { Factor out a perfect square. }} \\ {h=4 \sqrt{21}} & \color {Red} {\text { Simplify: } \sqrt{16}=4}\end{array} \nonumber \]
Дайте відповідь на питання. Сходи тягнеться$4 \sqrt{21}$ ногами вгору по стіні. За допомогою калькулятора це приблизно$18.3$ фути, округлені до найближчої десятої частини фута.
Озирніться назад. Зрозумійте, що коли ми використовуємо$18.3$ ft, наближення, наше рішення перевірить лише приблизно.

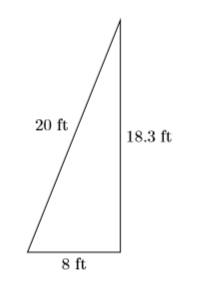
$рис. 8.2.7.png$

Використання теореми Піфагора:\[\begin{array}{r}{8^{2}+18.3^{2} \stackrel{?}{=} 20^{2}} \\ {64+334.89 \stackrel{?}{=} 400} \\ {398.89 \stackrel{?}{=} 400}\end{array} \nonumber \] наближення не є ідеальним, але здається досить близьким, щоб прийняти це рішення.

Вправа$\PageIndex{6}$

Сходи$15$ ноги довго спирається на стіну. Якщо основа сходів знаходиться в$6$ ногах від стіни, наскільки високо вгору по стіні досягає сходи? Використовуйте калькулятор, щоб округлити відповідь до найближчої десятої частини фута.

Відповідь: $13.7$стопи.