9.1: Функція квадратного кореня
- Page ID
- 58036
У цьому розділі звернемо увагу на функцію квадратного кореня, функцію, визначену рівнянням
\[\begin{array}{c} {f(x)= \sqrt{x}}\\ \end{array}\]
Починаємо розділ з малювання графіка функції, потім звертаємося до домену і діапазону. Після цього ми дослідимо ряд різних перетворень функції.
Графік функції квадратного кореня
Давайте створимо таблицю точок, які задовольняють рівнянню функції, а потім побудуємо точки з таблиці на декартовій системі координат на графічному папері. Ми продовжимо створювати та будувати точки, поки не переконаємося в можливій формі графіка.
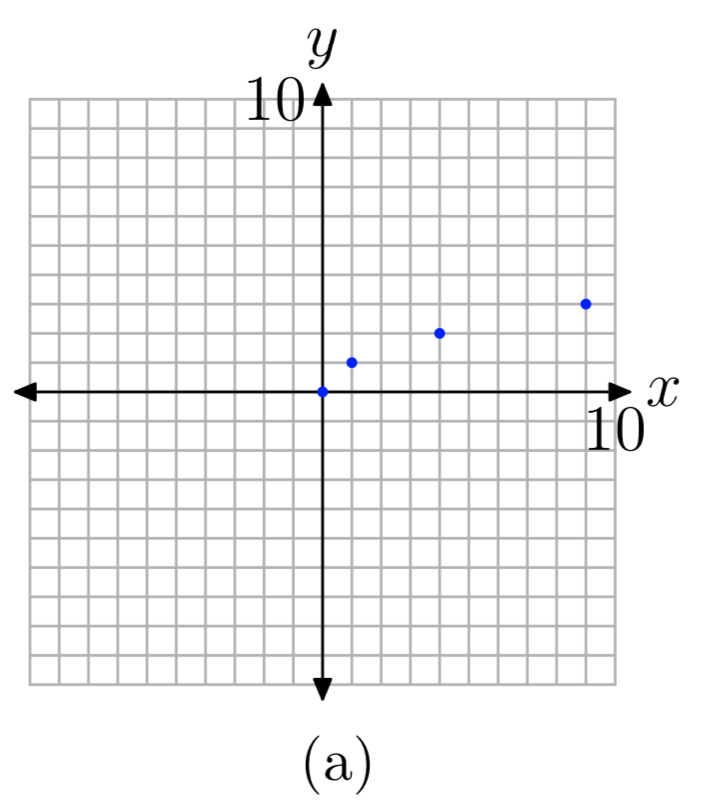
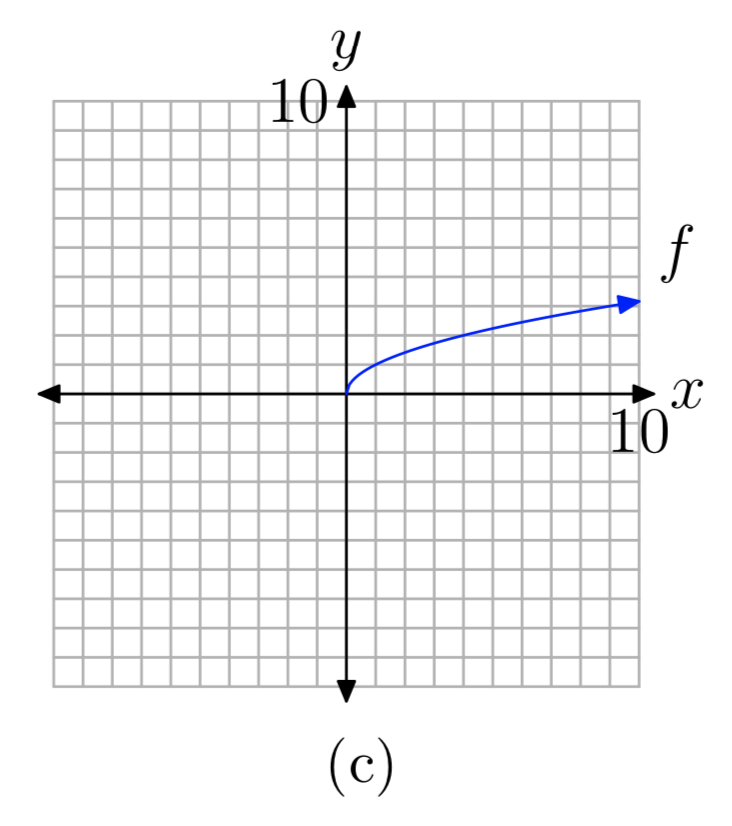
Ми знаємо, що не можемо взяти квадратний корінь від'ємного числа. Тому ми не хочемо ставити будь-які негативні x -значення в нашій таблиці. Щоб ще більше спростити наші обчислення, давайте використаємо числа, квадратний корінь яких легко обчислюється. Це приносить на розум ідеальні квадрати, такі як 0, 1, 4, 9 і так далі. Ми розмістили ці числа як x -значення в таблиці на малюнку 1 (b), потім обчислили квадратний корінь кожного. На малюнку 1 (а) ви бачите кожну з точок таблиці, побудовану як суцільна точка. Якщо ми продовжимо додавати точки до таблиці, побудувати їх, графік в кінцевому підсумку заповниться і прийме форму твердої кривої, показаної на малюнку 1 (c).
Точковий підхід побудови, який використовується для малювання графіка на\(f(x) = \sqrt{x}\) малюнку 1, є перевіреною та знайомою процедурою. Однак більш складний підхід передбачає розроблену в попередньому розділі теорію інверсів.
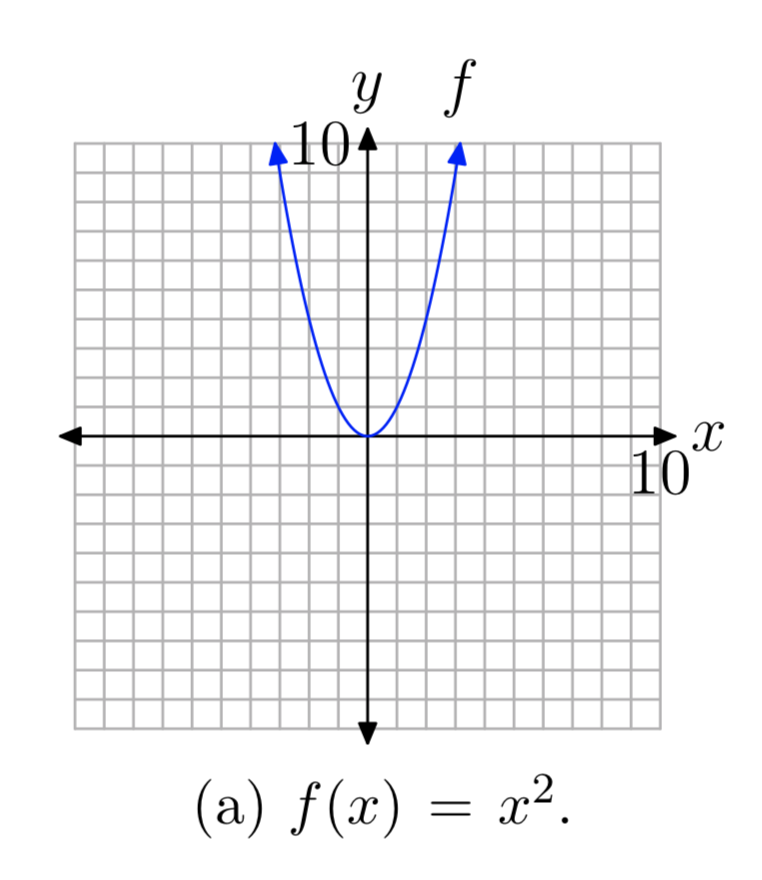
У певному сенсі взяття квадратного кореня - це «зворотне» квадратування. Ну, не зовсім, оскільки функція квадратури на\(f(x) = x^2\) малюнку 2 (а) не проходить тест горизонтальної лінії і не є один-до-одному. Однак якщо обмежити область квадратної функції, то графік на\(f(x) = x^2\) малюнку 2 (b), де\(x \ge 0\), дійсно проходить тест горизонтальної лінії і є один до одного. Отже, графік\(f(x) = x^2\), має зворотну\(x \ge 0\), а графік його зворотного знаходить шляхом відображення графіка\(f(x) = x^2\),\(x \ge 0\), поперек лінії y = x (див. Рис. 2 (в)).
Щоб знайти рівняння зворотного, нагадаємо, що процедура вимагає перемикання ролей x і y, потім вирішуємо отримане рівняння для y. Таким чином, спочатку пишіть\(f(x) = x^2\)\(x \ge 0\), в формі
\[\begin{array}{c} {y = x^2, x \ge 0}\\ \nonumber \end{array}\]
Далі перемикаємо x і y.
\[\begin{array}{c} {x = y^2, y \ge 0}\\ \end{array}\]
Коли ми вирішимо це останнє рівняння для y, ми отримуємо два рішення,
\[\begin{array}{c} {y = \pm\sqrt{x}}\\ \end{array}\]
Однак у рівнянні (2) зверніть увагу, що y повинен бути більше або дорівнює нулю. Отже, ми повинні вибрати невід'ємну відповідь у рівнянні (3), тому зворотне\(f(x) = x^2\)\(x \ge 0\), має рівняння
\[\begin{array}{c} {f^{−1}(x) = \sqrt{x}}\\ \nonumber \end{array}\]
Це рівняння відображення графіка того\(f(x) = x^2\)\(x \ge 0\), що зображено на малюнку 2 (в). Зверніть увагу на точну узгодженість з графіком функції квадратного кореня на малюнку 1 (c).
Послідовність графіків на малюнку 2 також допомагає нам визначити область і діапазон функції квадратного кореня.
- На малюнку 2 (а) парабола відкривається назовні на невизначений термін, як вліво, так і вправо. Отже, домен є\(D_{f} = (−\infty, \infty)\), або всі дійсні числа. Крім того, граф має вершину на початку і відкривається вгору нескінченно довго, тому діапазон є\(R_{f} = [0, \infty)\).
- На малюнку 2 (b) ми обмежили домен. Таким чином, граф\(f(x) = x^2\)\(x \ge 0\), тепер має домен\(D_{f} = [0, \infty)\). Діапазон незмінний і є\(R_{f} = [0, \infty)\).
- На малюнку 2 (c) ми відобразили графік\(f(x) = x^2\)\(x \ge 0\), через лінію y = x, щоб отримати графік\(f^{−1}(x) = \sqrt{x}\). Тому що ми поміняли роль х і у, область квадратного кореневої функції повинен дорівнювати діапазону\(f(x) = x^2\),\(x \ge 0\). Тобто,\(D_{f^{−1}} =[0,\infty)\) .Аналогічно, діапазон функції квадратного кореня повинен дорівнювати області\(f(x) = x^2\),\(x \ge 0\). Отже,\(R_{f^{−1}} = [0,\infty)\).
Звичайно, ми також можемо визначити область і діапазон функції квадратного кореня, проектуючи всі точки на графіку на осі x - і y, як показано на малюнках 3 (a) і (b) відповідно.
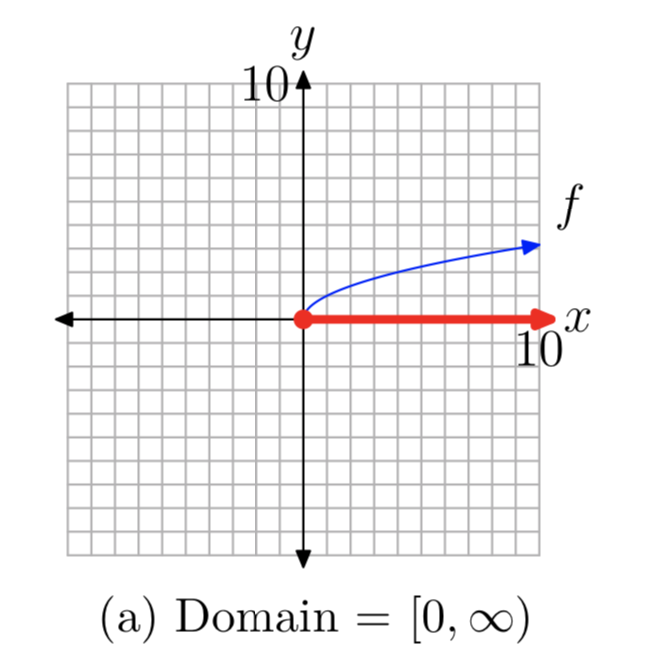
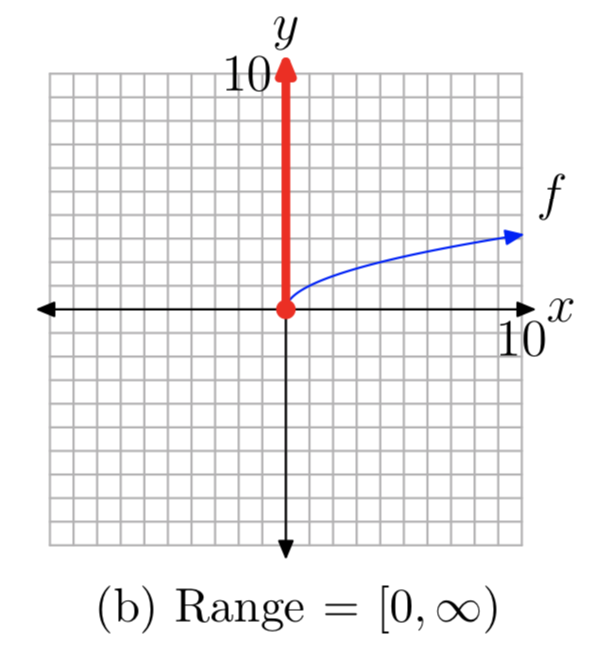
Деякі можуть заперечити проти діапазону, запитуючи «Як ми знаємо, що графік зображення функції квадратного кореня на малюнку 3 (b) піднімається на невизначений термін?» Знову ж таки, відповідь криється в послідовності графіків на малюнку 2. На малюнку 2 (c) зверніть увагу, що графік\(f(x) = x^2\)\(x \ge 0\), відкривається на невизначений час праворуч, коли графік піднімається до нескінченності. Отже, після відображення цього графіка через лінію y = x, отриманий графік повинен нескінченно підніматися вгору, коли він рухається вправо. Таким чином, діапазон функції квадратного кореня дорівнює\([0, \infty)\).
Переклади
Якщо ми зрушуємо графік\(y = \sqrt{x}\) вправо і вліво, або вгору і вниз, область і/або діапазон будуть порушені.
Приклад\(\PageIndex{4}\)
Намалюйте графік\(f(x) = \sqrt{x−2}\). Використовуйте графік для визначення домену та діапазону.
Ми знаємо, що основне рівняння\(y=\sqrt{x}\) має графік, показаний на малюнках 1 (c). Якщо замінити x на x − 2, то базове рівняння\(y=\sqrt{x}\) becomes \(f(x) = \sqrt{x−2}\). З нашої попередньої роботи з геометричними перетвореннями ми знаємо, що це змістить графік на дві одиниці вправо, як показано на малюнках 4 (a) і (b).
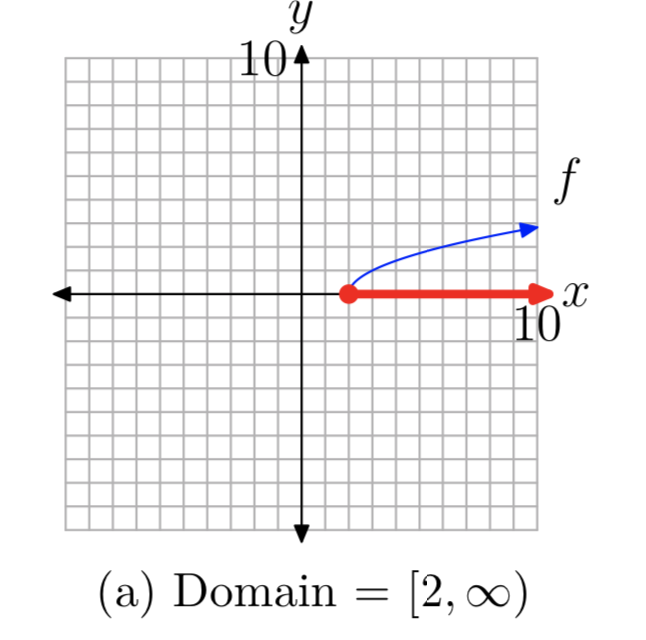
Щоб знайти домен, ми проектуємо кожну точку на графіку f на вісь x, як показано на малюнку 4 (а). Зверніть увагу, що всі точки праворуч від або включаючи 2 затінені на осі x. Отже, доменом f є
Домен\([2, \infty)\) = {x:\(x \ge 0\)}
Оскільки не було зрушення у вертикальному напрямку, діапазон залишається колишнім. Щоб знайти діапазон, ми проектуємо кожну точку на графіку на вісь y, як показано на малюнку 4 (b). Зауважте, що всі точки на нулі і вище нуля затінені на осі y. Таким чином, діапазон f дорівнює
Діапазон\([0,\infty)\) = {y:\(y \ge 0\)}.
Ми можемо знайти область цієї функції алгебраїчно, вивчивши її визначальне рівняння\(f(x) = \sqrt{x−2}\). Ми розуміємо, що не можемо взяти квадратний корінь від'ємного числа. Тому вираз під радикалом має бути невід'ємним (позитивним або нульовим). Тобто,
\(x − 2 \ge 0\).
Розв'язуючи цю нерівність для x,
\(x \ge 2\).
Таким чином, доменом f є Domain =\([2, \infty)\), що відповідає графічному рішенню вище.
Давайте розглянемо інший приклад.
Приклад\(\PageIndex{5}\)
Намалюйте графік\(f (x) = \sqrt{x + 4} + 2\). Використовуйте свій графік для визначення домену та діапазону f.
Знову ж таки, ми знаємо, що\(y=\sqrt{x}\) основне рівняння має графік, показаний на малюнку 1 (c). Якщо замінити x на x +4, основне рівняння\(y=\sqrt{x}\) стане\(y=\sqrt{x+4}\). З нашої попередньої роботи з геометричними перетвореннями ми знаємо, що це змістить графік\(y=\sqrt{x}\) чотирьох одиниць вліво, як показано на малюнку 5 (а).
Якщо ми знаємо, що додати 2\(y=\sqrt{x+4}\) до рівняння для отримання рівняння\(y=\sqrt{x+4} + 2\), це змістить графік\(y=\sqrt{x+4}\) двох одиниць вгору, як показано на малюнку 5 (b).
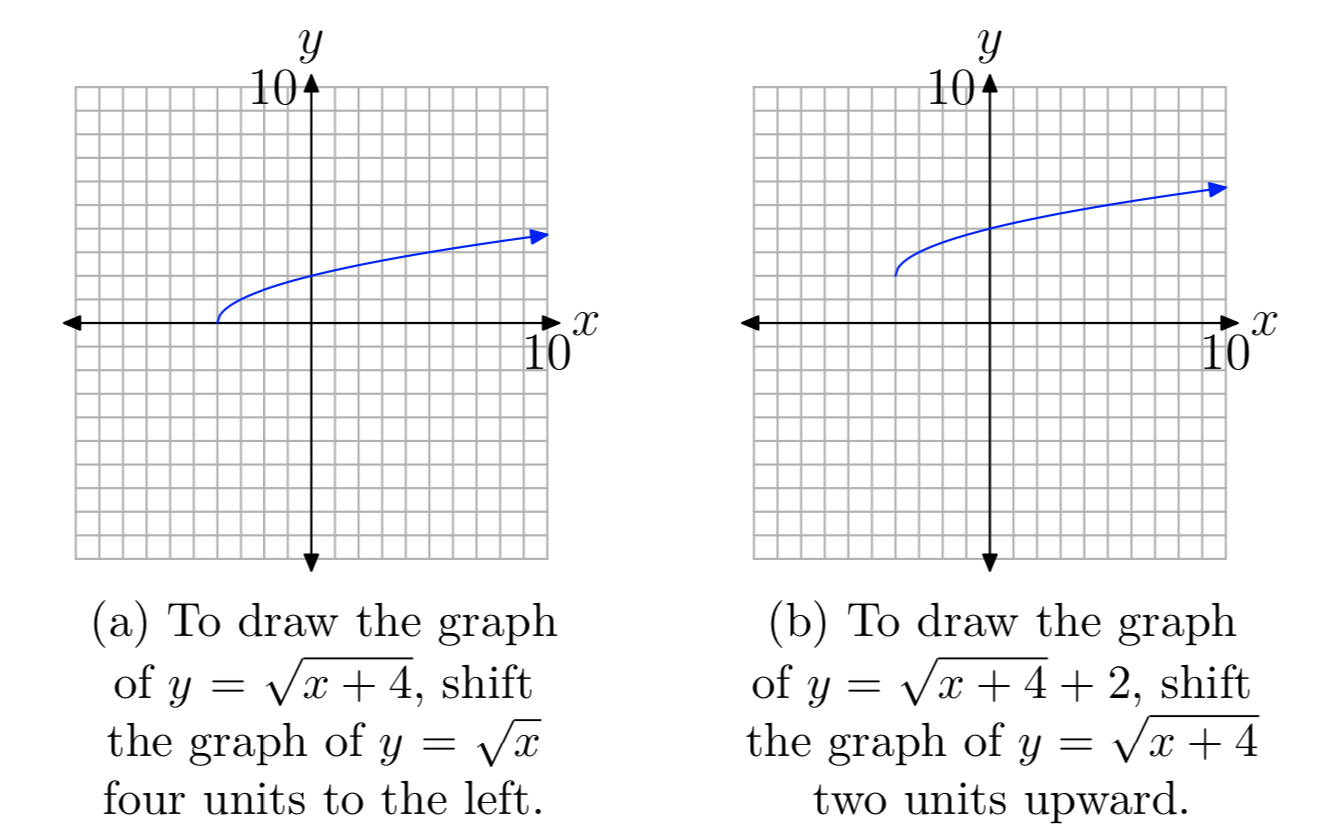
Щоб визначити область\(f (x) = \sqrt{x + 4} + 2\), ми проектуємо всі точки на графіку f на вісь x, як показано на малюнку 6 (а). Зауважте, що всі точки праворуч від або включаючи − 4 затінені на осі x. Таким чином, домен\(f (x) = \sqrt{x + 4} + 2\) є
Домен\([−4, \infty)\) = {x:\(x \ge −4\)}
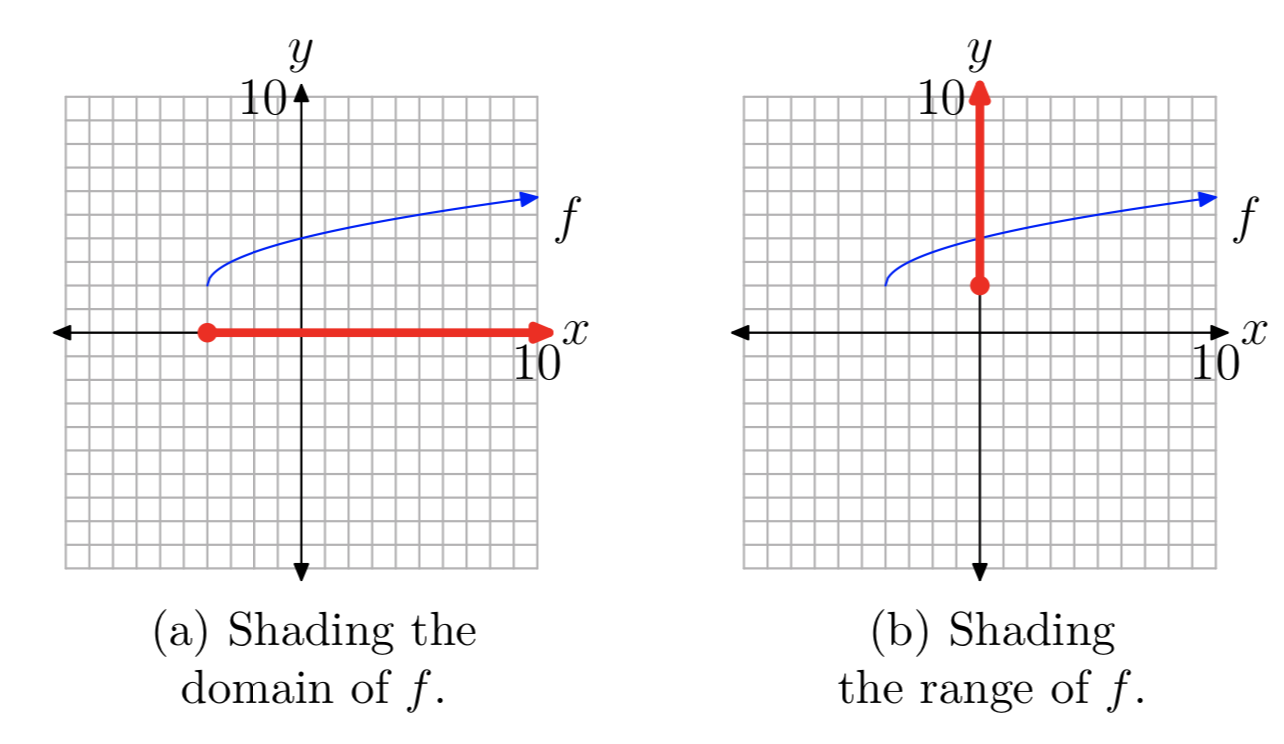
Аналогічно, щоб знайти діапазон f, спроектуйте всі точки на графіку f на вісь y, як показано на малюнку 6 (b). Зауважте, що всі точки на осі y, більші за або включаючи 2, затінені. Отже, діапазон f дорівнює
Діапазон\([2, \infty)\) = {y:\(y \ge 2\)}
Ми також можемо знайти область f алгебраїчно, вивчивши рівняння\(f (x) = \sqrt{x + 4} + 2\). Ми не можемо взяти квадратний корінь від'ємного числа, тому вираз під радикалом має бути невід'ємним (нульовим або позитивним). Отже,
\(x + 4 \ge 0\).
Розв'язуючи цю нерівність для x,
\(x \ge −4\).
Таким чином, доменом f є Domain =\([−4,\infty)\), що відповідає графічному рішенню, представленому вище.
Роздуми
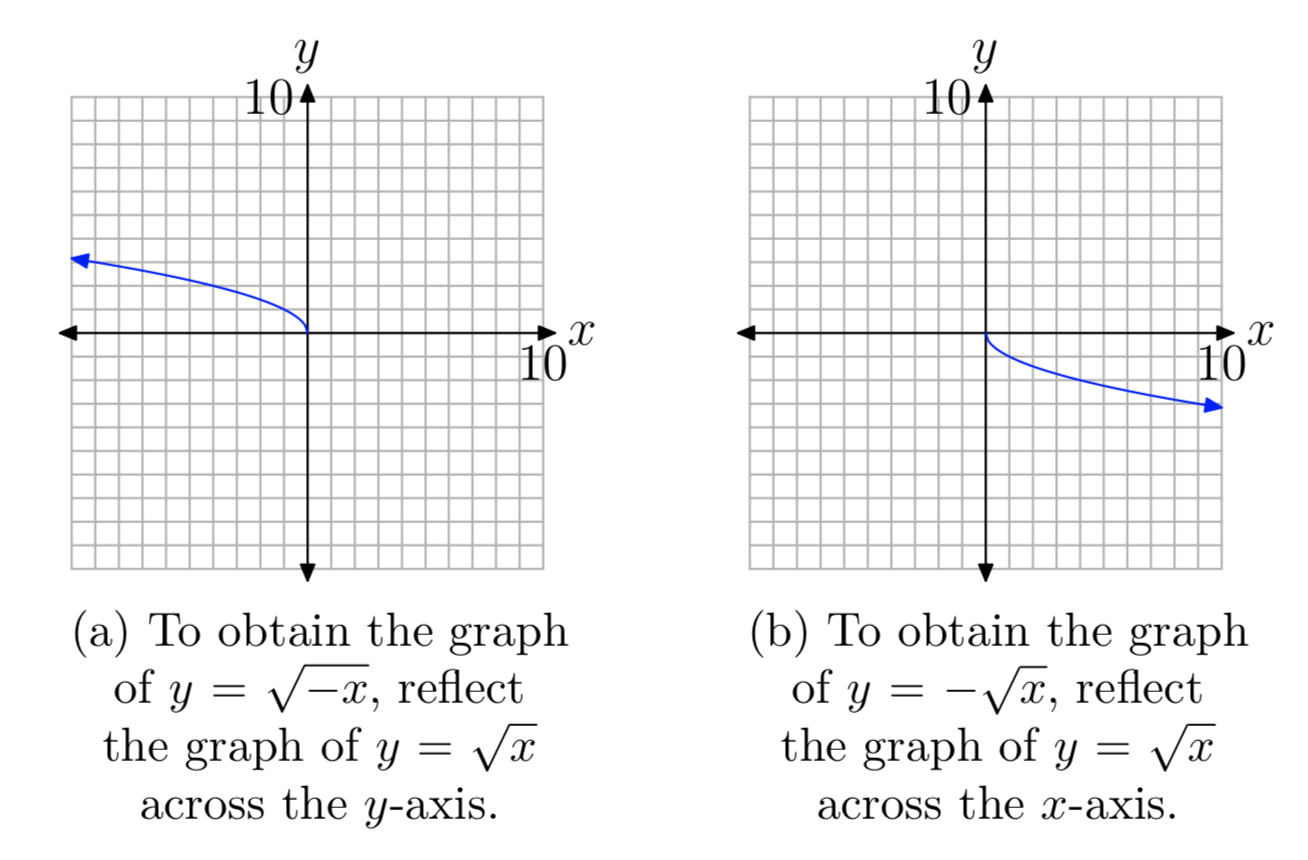
Якщо почати з базового рівняння\(y = \sqrt{x}\), то замінити x на −x, тоді графік отриманого рівняння\(y = \sqrt{−x}\) захоплюється відображенням графіка\(y = \sqrt{x}\) (див. Рис. 1 (c)) по горизонталі по осі y. Графік\(y = \sqrt{−x}\) показаний на малюнку 7 (а).
Аналогічно, графік\(y = −\sqrt{x}\) буде вертикальним відображенням графіка\(y = \sqrt{x}\) поперек осі x, як показано на малюнку 7 (b).
Найчастіше вас попросять виконати рефлексію і переклад.
Приклад\(\PageIndex{6}\)
Намалюйте графік\(f(x) = \sqrt{4− x}\). Використовуйте отриманий графік для визначення області та діапазону f.
Спочатку перепишіть рівняння\(f(x) = \sqrt{4− x}\) наступним чином:
\(f(x) = \sqrt{−(x−4)}\)
Визначення
Перші роздуми. Зазвичай більш інтуїтивно виконувати роздуми перед перекладами.
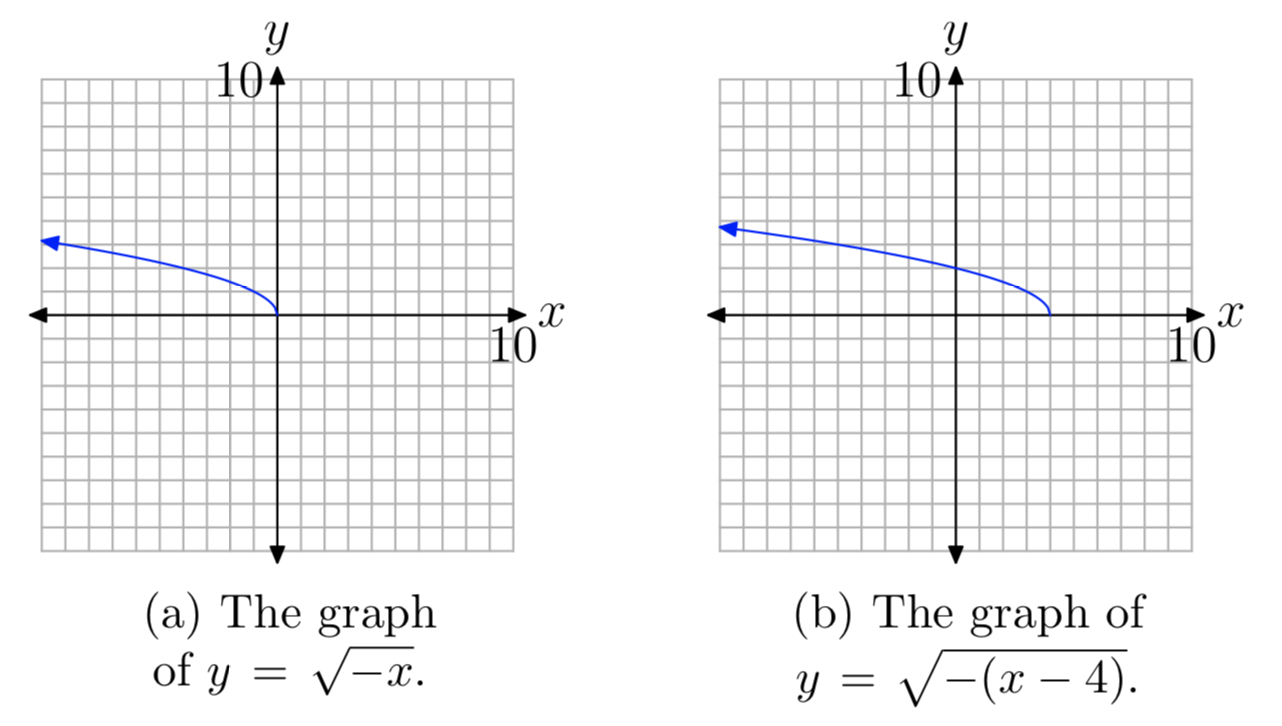
Маючи на увазі цю думку, ми спочатку накидаємо графік\(f(x) = \sqrt{−x}\), який є відображенням графіка\(f(x) = \sqrt{x}\) поперек осі y. Це показано на малюнку 8 (а).
Тепер\(f(x) = \sqrt{−x}\) замініть x на x − 4, щоб отримати\(f(x) = \sqrt{−(x−4)}\). Це зміщує графік\(f(x) = \sqrt{−x}\) чотирьох одиниць вправо, як показано на малюнку 8 (b).
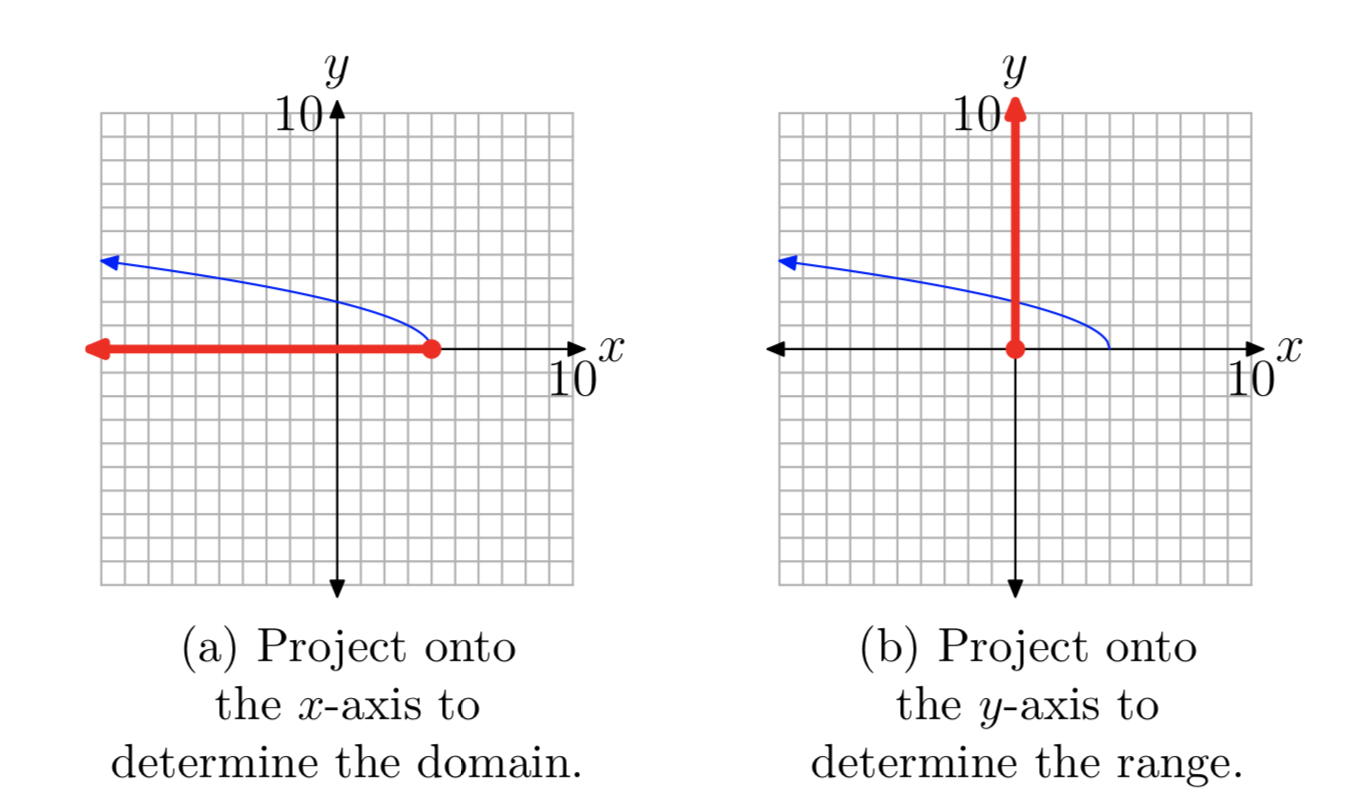
Щоб знайти область функції\(f(x) = \sqrt{−(x−4)}\), або еквівалентно\(f(x) = \sqrt{4−x}\), спроектуйте кожну точку на графіку f на вісь x, як показано на малюнку 9 (a). Зауважте, що всі дійсні числа, менші або рівні 4, затінені на осі x. Отже, доменом f є
Домен\((−\infty, 4]\) = {x:\(x \le 4\)}.
Аналогічно, щоб отримати діапазон f, проектуйте кожну точку на графіку f на їхню вісь, як показано на малюнку 9 (b). Зверніть увагу, що всі дійсні числа, більші або рівні нулю, затінені на осі y. Значить, діапазон f дорівнює
Діапазон\([0,\infty)\) = {x:\(x \ge 0\)}.
Ми також можемо знайти область функції f, вивчивши рівняння\(f(x) = \sqrt{4−x}\). Ми не можемо взяти квадратний корінь від'ємного числа, тому вираз під радикалом має бути невід'ємним (нульовим або позитивним). Отже,
\(4 − x \ge 0\).
Розв'яжіть цю останню нерівність для x. Спочатку відніміть 4 з обох сторін нерівності, потім помножте обидві сторони отриманої нерівності на − 1. Звичайно, множення на негативне число змінює символ нерівності.
\(−x \ge −4\)
\(x \le 4\)
Таким чином, домен f дорівнює {x:\(x \le 4\)}. У інтервальній нотації, Domain =\((−\infty, 4]\). Це добре погоджується з графічним результатом, знайденим вище.
Найчастіше для визначення області функції квадратного кореня знадобиться комбінація графічного калькулятора та невелика алгебраїчна маніпуляція.
Приклад\(\PageIndex{7}\)
Намалюйте графік\(f(x) = \sqrt{5−2x}\) Використовуйте графік та алгебраїчну техніку для визначення області функції.
Завантажте функцію в Y1 в меню Y= вашого калькулятора, як показано на малюнку 10 (a). Виберіть 6: ZStandard з меню ZOOM, щоб створити графік, показаний на малюнку 10 (b).
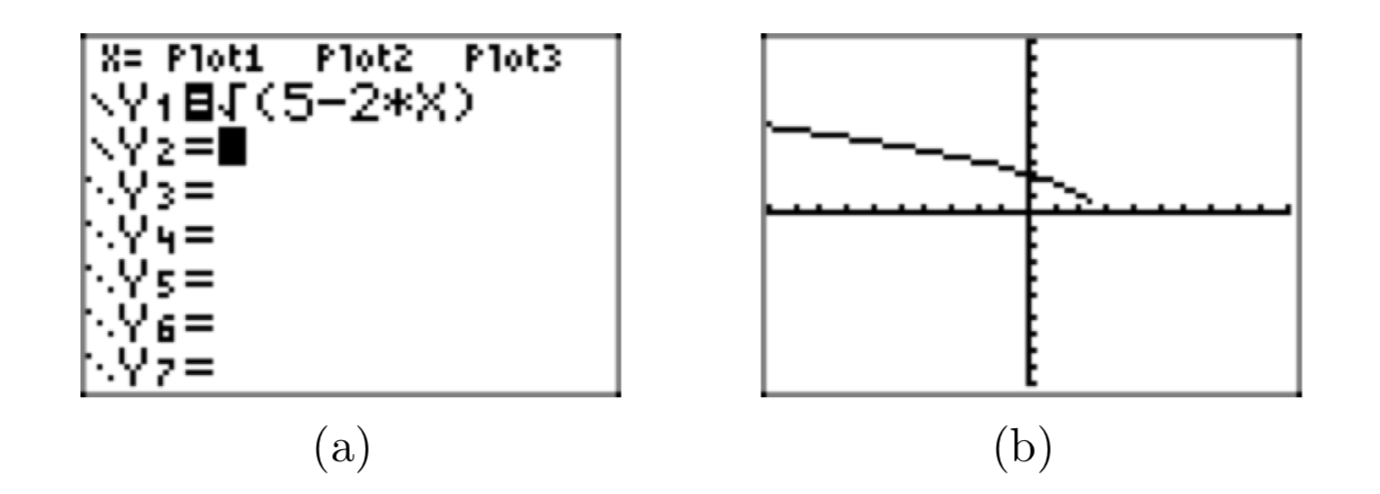
Подивіться уважно на графік на малюнку 10 (b) і зауважте, що важко сказати, чи опускається графік, щоб «торкнутися» осі x поблизу\(x \approx 2.5\). Однак наш попередній досвід роботи з функцією квадратного кореня змушує нас вважати, що це всього лише артефакт недостатньої роздільної здатності на калькуляторі, який заважає графіку «торкнутися» осі x в\(x \approx 2.5\).
Алгебраїчний підхід дозволить вирішити питання. Визначити область f можна, вивчивши рівняння\(f(x) = \sqrt{5 − 2x}\). Отже, Ми не можемо взяти квадратний корінь від'ємного числа, тому вираз під радикалом має бути невід'ємним (нульовим або додатним).
\(5 − 2x \ge 0\).
Розв'яжіть цю останню нерівність для x. Спочатку відніміть 5 з обох сторін нерівності.
\(−2x \ge −5\).
Далі розділіть обидві сторони цієї останньої нерівності на −2. Пам'ятайте, що ми повинні змінити нерівність в той момент, коли ми ділимо на негативне число.
\(\frac{−2x}{−2} \le \frac{−5}{−2}\).
\(x \le \frac{5}{2}\).
Таким чином, домен f дорівнює {x:\(x \le \frac{5}{2}\)}. У інтервальній нотації, Domain =\((−\infty, \frac{5}{2}]\). Це добре погоджується з графічним результатом, знайденим вище.
Подальший самоаналіз показує, що цей аргумент також вирішує питання про те, чи «торкається» графік до осі x\(x= \frac{5}{2}\). Якщо ви залишитеся непереконаними, то підставляйте,\(x=\frac{5}{2}\)\(f(x) = \sqrt{5−2x}\) щоб побачити
\(f(\frac{5}{2})= \sqrt{5−2(\frac{5}{2})} =\sqrt{0} = 0\).
Таким чином, графік f «торкається» осі х в точці\((\frac{5}{2}, 0)\).
У вправі 1-10 виконайте кожне з наступних завдань:
- Налаштуйте систему координат на аркуші графічного паперу. Позначте та масштабуйте кожну вісь.
- Заповніть таблицю балів за заданою функцією. Побудуйте кожну з точок у вашій системі координат, а потім використовуйте їх, щоб допомогти намалювати графік заданої функції.
- Використовуйте різні кольорові олівці, щоб спроектувати всі точки на осі x - і y, щоб визначити область і діапазон. Використовуйте інтервальне позначення для опису do- main заданої функції.
Вправа\(\PageIndex{1}\)
\(f(x) = −\sqrt{x}\)
|
х |
0 |
1 |
4 |
9 |
|
f (х) |
- Відповідь
-
х
0
1
4
9
f (х)
0
− 1
− 2
− 3
Побудуйте точки в таблиці і використовуйте їх, щоб допомогти намалювати графік.
Спроектуйте всі точки на графіку на вісь x, щоб визначити область: Domain =\([0, \infty)\). Спроектуйте всі точки на графіку на вісь y, щоб визначити діапазон: Range =\((−\infty, 0]\).
Вправа\(\PageIndex{2}\)
\(f(x) = \sqrt{−x}\)
|
х |
0 |
− 1 |
− 4 |
− 9 |
|
f (х) |
Вправа\(\PageIndex{3}\)
\(f(x)= \sqrt{x+2}\)
|
х |
− 2 |
− 1 |
2 |
7 |
|
f (х) |
- Відповідь
-
х
− 2
− 1
2
7
f (х)
0
1
2
3
Побудуйте точки в таблиці і використовуйте їх, щоб допомогти намалювати графік.
Спроектуйте всі точки на графіку на вісь x, щоб визначити область: Domain =\([−2, \infty)\). Спроектуйте всі точки на графіку на вісь y, щоб визначити діапазон: Range =\([0, \infty)\).
Вправа\(\PageIndex{4}\)
\(f(x)= \sqrt{5−x}\)
|
х |
− 4 |
1 |
4 |
5 |
|
f (х) |
Вправа\(\PageIndex{5}\)
\(f(x)= \sqrt{x}+2\)
|
х |
0 |
1 |
4 |
9 |
|
f (х) |
- Відповідь
-
х
0
1
4
9
f (х)
2
3
4
5
Покладіть точки в таблиці і використовуйте їх, щоб намалювати графік f.
Спроектуйте всі точки на графіку на вісь x, щоб визначити область: Domain =\([0, \infty)\). Спроектуйте всі точки на графіку на вісь y, щоб визначити діапазон: Range =\([2, \infty)\).
Вправа\(\PageIndex{6}\)
\(f(x)=\sqrt{x}−1\)
|
х |
0 |
1 |
4 |
9 |
|
f (х) |
Вправа\(\PageIndex{7}\)
\(f(x)= \sqrt{x+3}+2\)
|
х |
− 3 |
− 2 |
1 |
6 |
|
f (х) |
- Відповідь
-
х
− 3
− 2
1
6
f (х)
2
3
4
5
Покладіть точки в таблиці і використовуйте їх, щоб намалювати графік f.
- Спроектуйте всі точки на графіку на вісь x, щоб визначити область: Domain =\([−3, \infty)\). Спроектуйте всі точки на графіку на вісь y, щоб визначити діапазон: Range =\([2, \infty)\).
Вправа\(\PageIndex{8}\)
\(f(x)= \sqrt{x−1}+3\)
|
х |
1 |
2 |
5 |
10 |
|
f (х) |
Вправа\(\PageIndex{9}\)
\(f(x)= \sqrt{3−x}\)
|
х |
− 6 |
− 1 |
2 |
3 |
|
f (х) |
- Відповідь
-
х
− 6
− 1
2
3
f (х)
3
2
1
0
Покладіть точки в таблиці і використовуйте їх, щоб намалювати графік f.
Спроектуйте всі точки на графіку на вісь x, щоб визначити область: Domain =\((−\infty, 3]\). Спроектуйте всі точки на графіку на вісь y, щоб визначити діапазон: Range =\([0, \infty)\).
Вправа\(\PageIndex{10}\)
\(f(x)=−\sqrt{x+3}\)
|
х |
− 3 |
− 2 |
1 |
6 |
|
f (х) |
У вправах 11 - 20 виконайте кожне з наступних завдань.
- Налаштуйте систему координат на аркуші графічного паперу. Позначте та масштабуйте кожну вісь. Не забудьте намалювати всі лінії лінійкою.
- Використовуйте геометричні перетворення, щоб намалювати графік заданої функції у вашій системі координат без використання графічного калькулятора. Примітка: Ви можете перевірити своє рішення за допомогою калькулятора, але ви повинні мати можливість створити графік без використання вашого калькулятора.
- Використовуйте різні кольорові олівці, щоб спроектувати точки на графіку функції на осі x - та y. Використовуйте інтервальне позначення для опису області та діапазону функції.
Вправа\(\PageIndex{11}\)
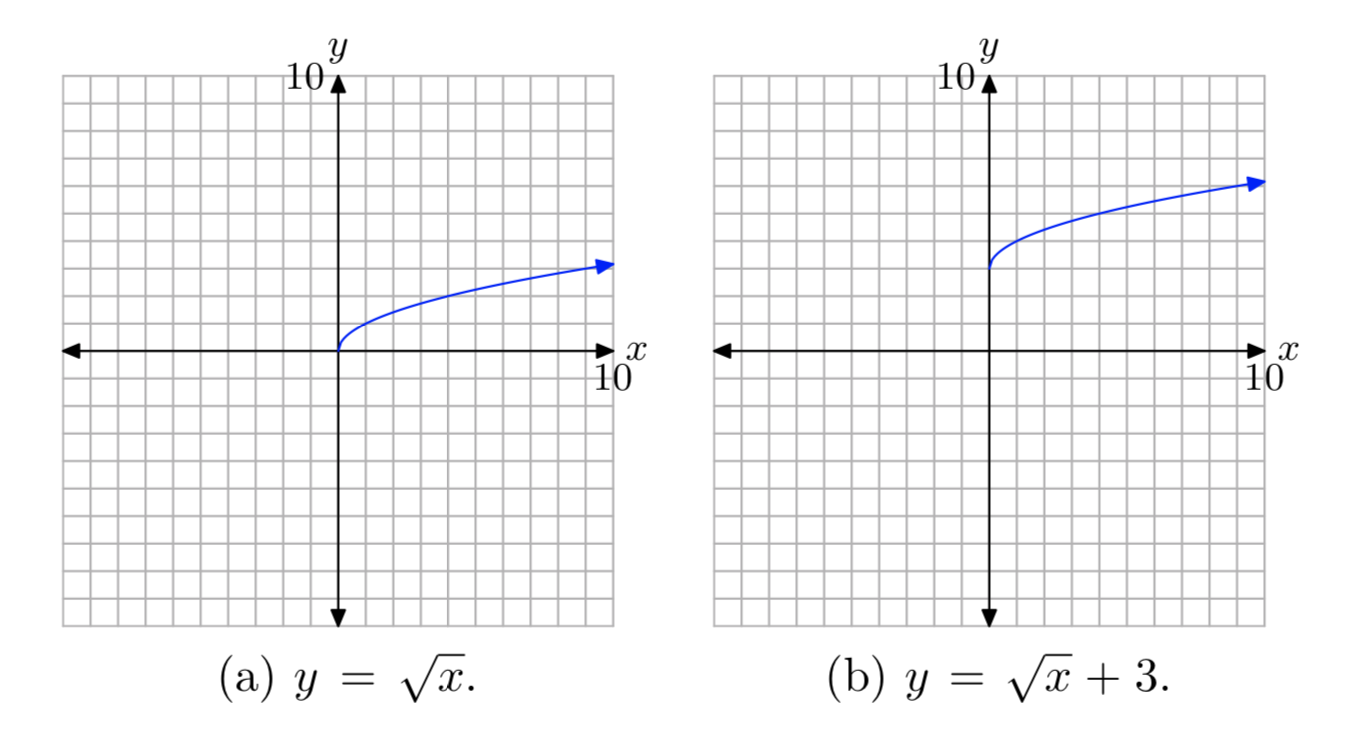
\(f(x)= \sqrt{x}+3\)
- Відповідь
-
Спочатку побудуйте графік\(y = \sqrt{x}\), як показано в (а). Потім додайте 3, щоб отримати рівняння\(y = \sqrt{x} + 3\). Це змістить графік\(y = \sqrt{x}\) вгору на 3 одиниці, як показано в (b).
Спроектуйте всі точки на графіку на вісь x, щоб визначити область: Domain =\([0, \infty)\). Спроектуйте всі точки на графіку на вісь y, щоб визначити діапазон: Range =\([3, \infty)\).
Вправа\(\PageIndex{12}\)
\(f(x)=\sqrt{x+3}\)
Вправа\(\PageIndex{13}\)
\(f(x)=\sqrt{x−2}\)
- Відповідь
-
Спочатку побудуйте графік\(y = \sqrt{x}\), як показано в (а). Потім замініть x на x − 2, щоб отримати рівняння\(y = \sqrt{x−2}\). Це змістить графік\(y = \sqrt{x}\) вправо на 2 одиниці, як показано в (b).
Спроектуйте всі точки на графіку на вісь x, щоб визначити область: Domain =\([2, \infty)\). Спроектуйте всі точки на графіку на вісь y, щоб визначити діапазон: Range =\([0, \infty)\).
Вправа\(\PageIndex{14}\)
\(f(x)=\sqrt{x}−2\)
Вправа\(\PageIndex{15}\)
\(f(x)= \sqrt{x+5}+1\)
- Відповідь
-
Спочатку побудуйте графік\(y = \sqrt{x}\), як показано в (а). Потім замініть x на x + 5, щоб отримати рівняння\(y = \sqrt{x+5}\). Потім додайте 1, щоб отримати рівняння\(f(x)= \sqrt{x+5}+1\). Це змістить графік вліво\(y = \sqrt{x}\) на 5 одиниць, потім вгору на 1 одиницю, як показано в (b).
Спроектуйте всі точки на графіку на вісь x, щоб визначити область: Domain =\([−5, \infty)\). Спроектуйте всі точки на графіку на вісь y, щоб визначити діапазон: Range =\([1, \infty)\).
Вправа\(\PageIndex{16}\)
\(f(x)=\sqrt{x−2}−1\)
Вправа\(\PageIndex{17}\)
\(y = −\sqrt{x + 4}\)
- Відповідь
-
Спочатку побудуйте графік\(y = \sqrt{x}\), як показано в (а). Потім, звести нанівець, щоб виробляти\(y = −\sqrt{x}\). Це буде відображати графік\(y = \sqrt{x}\) поперек осі x, як показано в (b). Нарешті, замініть x на x + 4, щоб отримати рівняння\(y = −\sqrt{x + 4}\). Це змістить графік\(y = −\sqrt{x}\) чотирьох одиниць вліво, як показано в (c).
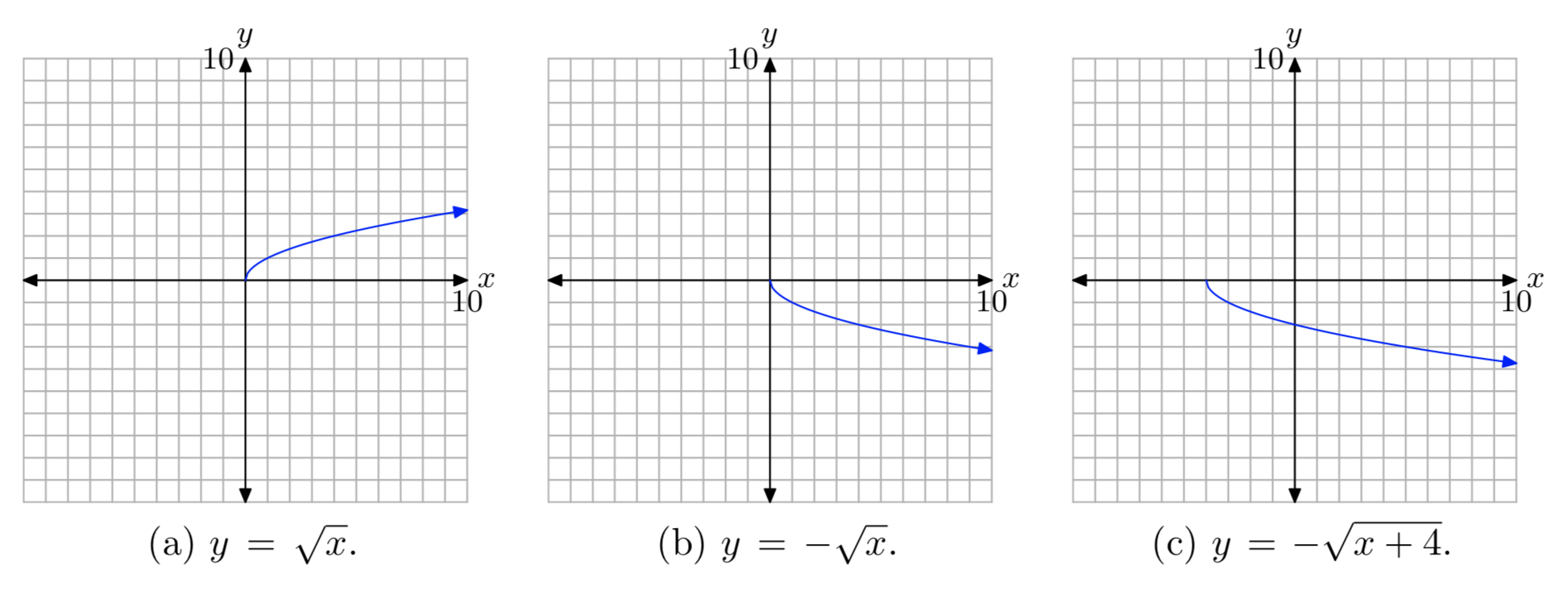
Спроектуйте всі точки на графіку на вісь x, щоб визначити область: Domain =\([−4, \infty)\). Спроектуйте всі точки на графіку на вісь y, щоб визначити діапазон: Range =\((−\infty, 0]\).
Вправа\(\PageIndex{18}\)
\(f(x)=−\sqrt{x}+4\)
Вправа\(\PageIndex{19}\)
\(f(x)=−\sqrt{x}+3\)
- Відповідь
-
Спочатку побудуйте графік\(y = \sqrt{x}\), як показано в (а). Потім, звести нанівець, щоб виробляти\(y = −\sqrt{x}\). Це буде відображати графік\(y = \sqrt{x}\) поперек осі x, як показано в (b). Нарешті, додайте 3, щоб отримати рівняння\(y=−\sqrt{x}+3\). Це змістить графік\(y = −\sqrt{x}\) трьох одиниць вгору, як показано в (c).
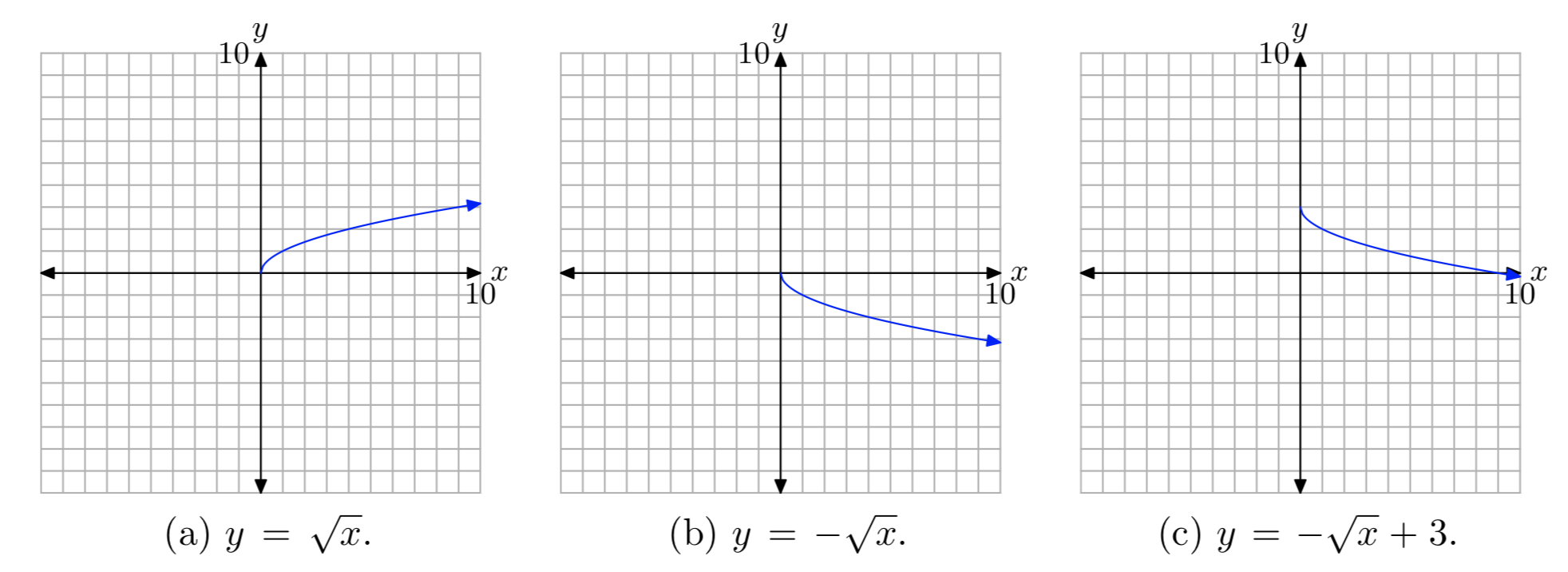
Спроектуйте всі точки на графіку на вісь x, щоб визначити область: Domain =\([0, \infty)\). Спроектуйте всі точки на графіку на вісь y, щоб визначити діапазон: Range =\((−\infty, 3]\).
Вправа\(\PageIndex{20}\)
\(f(x)=−\sqrt{x+3}\)
Вправа\(\PageIndex{21}\)
Щоб намалювати графік функції\(f(x) = \sqrt{3−x}\), виконайте кожен з наступних кроків послідовно без допомоги калькулятора.
- Налаштуйте систему координат і намалюйте графік\(y = \sqrt{x}\). Позначте графік його рівнянням.
- Налаштуйте другу систему координат і намалюйте графік\(y = \sqrt{−x}\). Позначте графік його рівнянням.
- Налаштуйте третю систему координат і намалюйте графік\(y =\sqrt{−(x − 3)}\). Позначте графік його рівнянням. Це графік\(y =\sqrt{3−x}\). Використовуйте інтервальне позначення для визначення домену та діапазону цієї функції.
- Відповідь
-
Спочатку побудуйте графік\(y = \sqrt{x}\), як показано в (а). Потім замініть x на − x, щоб отримати рівняння\(y = \sqrt{−x}\). Це буде відображати графік\(y = \sqrt{x}\) поперек осі y, як показано в (b). Нарешті, замініть x на x − 3, щоб отримати рівняння\(y = \sqrt{−(x − 3)}\). Це змістить графік\(y = \sqrt{−x}\) трьох одиниць вправо, як показано в (c).
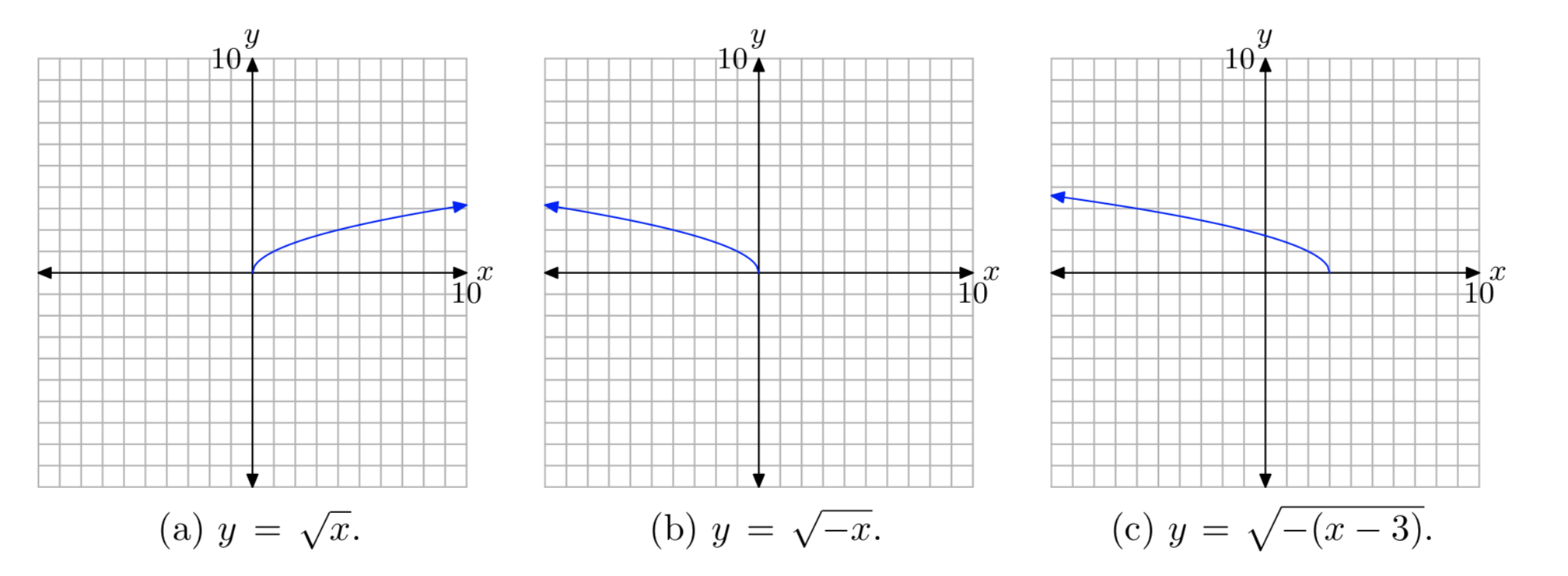
Спроектуйте всі точки на графіку на вісь x, щоб визначити область: Domain =\((−\infty, 3]\). Спроектуйте всі точки на графіку на вісь y, щоб визначити діапазон: Range =\([0, \infty)\).
Вправа\(\PageIndex{22}\)
Щоб намалювати графік функції\(f(x) = \sqrt{−x−3}\), виконайте послідовно кожен з наступних кроків.
- Налаштуйте систему координат і намалюйте графік\(y = \sqrt{x}\). Позначте графік його рівнянням.
- Налаштуйте другу систему координат і намалюйте графік\(y = \sqrt{−x}\). Позначте графік його рівнянням.
- Налаштуйте третю систему координат і намалюйте графік\(y =\sqrt{−(x + 3)}\). Позначте графік його рівнянням. Це графік\(y =\sqrt{−x−3}\). Використовуйте інтервальне позначення для визначення домену та діапазону цієї функції.
Вправа\(\PageIndex{23}\)
Щоб намалювати графік функції\(f(x) = \sqrt{−x−3}\), виконайте кожен з наступних кроків послідовно без допомоги калькулятора.
- Налаштуйте систему координат і намалюйте графік\(y = \sqrt{x}\). Позначте графік його рівнянням.
- Налаштуйте другу систему координат і намалюйте графік\(y = \sqrt{−x}\). Позначте графік його рівнянням.
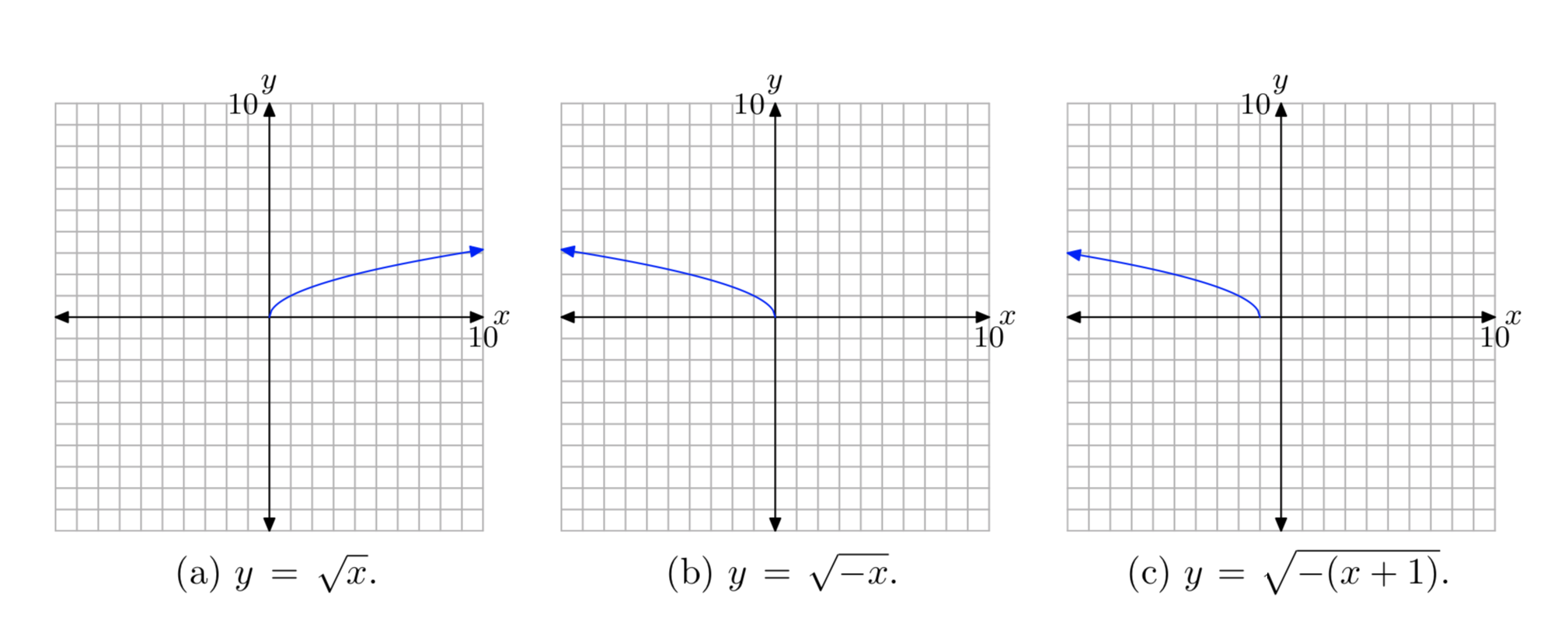
- Налаштуйте третю систему координат і намалюйте графік\(y =\sqrt{−(x + 1)}\). Позначте графік його рівнянням. Це графік\(y =\sqrt{−x−1}\). Використовуйте інтервальне позначення для визначення домену та діапазону цієї функції.
- Відповідь
-
Спочатку побудуйте графік\(y = \sqrt{x}\), як показано в (а). Потім замініть x на −x, щоб отримати рівняння\(y = \sqrt{−x}\). Це буде відображати графік\(y = \sqrt{x}\) поперек осі y, як показано в (b). Нарешті, замініть x на x + 1, щоб отримати рівняння\(y = \sqrt{−(x + 1)}\). Це змістить графік\(y = \sqrt{−x}\) однієї одиниці вліво, як показано в (c).
Спроектуйте всі точки на графіку на вісь x, щоб визначити область: Domain =\((−\infty, −1]\). Спроектуйте всі точки на графіку на вісь y, щоб визначити діапазон: Range =\([0, \infty)\).
Вправа\(\PageIndex{24}\)
Щоб намалювати графік функції\(f(x) = \sqrt{1−x}\), виконайте послідовно кожен з наступних кроків.
- Налаштуйте систему координат і намалюйте графік\(y = \sqrt{x}\). Позначте графік його рівнянням.
- Налаштуйте другу систему координат і намалюйте графік\(y = \sqrt{−x}\). Позначте графік його рівнянням.
- Налаштуйте третю систему координат і намалюйте графік\(y =\sqrt{−(x−1)}\). Позначте графік його рівнянням. Це графік\(y =\sqrt{1−x}\). Використовуйте інтервальне позначення для визначення домену та діапазону цієї функції.
У вправах 25 - 28 виконайте кожне з наступних завдань.
- Намалюйте графік заданої функції за допомогою графічного калькулятора. Скопіюйте зображення у вікні перегляду на домашній папір. Позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax. Позначте свій графік його рівнянням. Використовуйте графік для визначення області функції і опису області з інтервальними позначеннями.
- Використовуйте чисто алгебраїчний підхід для визначення області даної функції. Використовуйте інтервальне позначення, щоб визначити результат. Чи згоден він з графічним результатом з частини 1?
Вправа\(\PageIndex{25}\)
\(f(x)= \sqrt{2x+7}\)
- Відповідь
-
Ми використовуємо графічний калькулятор для отримання наступного графіка\(f(x)= \sqrt{2x+7}\)
Ми оцінюємо, що домен буде складатися з усіх дійсних чисел праворуч приблизно − 3. 5. Щоб знайти алгебраїчне рішення, зверніть увагу, що ви не можете взяти квадратний корінь від'ємного числа. Значить, вираз під радикалом in\(f(x)= \sqrt{2x+7}\) має бути більше або дорівнює нулю.
\(2x + 7 \ge 0\)
\(2x \ge −7\)
\(x \ge −\frac{7}{2}\)
Отже, домен є\([−\frac{7}{2}, \infty)\).
Вправа\(\PageIndex{26}\)
\(f(x)= \sqrt{7−2x}\)
Вправа\(\PageIndex{27}\)
\(f(x)= \sqrt{12−4x}\)
- Відповідь
-
Ми використовуємо графічний калькулятор для отримання наступного графіка\(f(x)= \sqrt{12−4x}\).
Ми вважаємо, що домен буде складатися з усіх дійсних чисел праворуч приблизно 3. Щоб знайти алгебраїчне рішення, зверніть увагу, що ви не можете взяти квадратний корінь від'ємного числа. Значить, вираз під радикалом in\(f(x)= \sqrt{12−4x}\) має бути більше або дорівнює нулю.
\(12−4x \ge 0\)
\(−4x \ge −12\)
\(x \le 3\)
Отже, домен є\((−\infty, 3]\).
Вправа\(\PageIndex{28}\)
\(f(x)= \sqrt{12+2x}\)
У Вправах 29 - 40 знайти область даної функції алгебраїчно.
Вправа\(\PageIndex{29}\)
\(f(x)= \sqrt{2x+9}\)
- Відповідь
-
Парний корінь від'ємного числа не визначається як дійсне число. Таким чином, 2x + 9 повинен бути більше або дорівнює нулю. Оскільки\(2x + 9 \ge 0\) має на увазі\(x \ge −\frac{9}{2}\), що домен є інтервалом\([−\frac{9}{2},\infty)\).
Вправа\(\PageIndex{30}\)
\(f(x)=\sqrt{−3x+3}\)
Вправа\(\PageIndex{31}\)
\(f(x)=\sqrt{−8x−3}\)
- Відповідь
-
Парний корінь від'ємного числа не визначається як дійсне число. Таким чином, −8x−3 має бути більшим або рівним нулю. Оскільки\(−8x−3 \ge 0\) має на увазі\(x \le −\frac{3}{8}\), що домен є інтервалом\((−\infty, −\frac{3}{8}]\).
Вправа\(\PageIndex{32}\)
\(f(x)=\sqrt{−3x+6}\)
Вправа\(\PageIndex{33}\)
\(f(x)=\sqrt{−6x−8}\)
- Відповідь
-
Парний корінь від'ємного числа не визначається як дійсне число. Таким чином, −6x−8 має бути більшим або рівним нулю. Оскільки\(−6x−8 \ge 0\) має на увазі\(x \le −\frac{4}{3}\), що домен є інтервалом\((−\infty, \frac{4}{3}]\).
Вправа\(\PageIndex{34}\)
\(f(x)=\sqrt{8x−6}\)
Вправа\(\PageIndex{35}\)
\(f(x)=\sqrt{−7x+2}\)
- Відповідь
-
Парний корінь від'ємного числа не визначається як дійсне число. Таким чином, −7x+2 має бути більше або дорівнює нулю. Оскільки\(−7x+2 \ge 0\) має на увазі\(x \le \frac{2}{7}\), що домен є інтервалом\((−\infty, \frac{2}{7}]\).
Вправа\(\PageIndex{36}\)
\(f(x)=\sqrt{8x−3}\)
Вправа\(\PageIndex{37}\)
\(f(x)=\sqrt{6x+3}\)
- Відповідь
-
Парний корінь від'ємного числа не визначається як дійсне число. Таким чином, 6х+3 повинен бути більше або дорівнює нулю. Оскільки\(6x+3 \ge 0\) має на увазі\(x \ge −\frac{1}{2}\), що домен є інтервалом\([−\frac{1}{2}, \infty)\).
Вправа\(\PageIndex{38}\)
\(f(x)=\sqrt{x−5}\)
Вправа\(\PageIndex{39}\)
\(f(x)=\sqrt{−7x−8}\)
- Відповідь
-
Парний корінь від'ємного числа не визначається як дійсне число. Таким чином, −7x−8 має бути більшим або рівним нулю. Оскільки\(−7x−8 \ge 0\) має на увазі\(x \le −\frac{8}{7}\), що домен є інтервалом\((−\infty, −\frac{8}{7}]\)
Вправа\(\PageIndex{40}\)
\(f(x)=\sqrt{7x+8}\)