8.5: Логарифмічні функції

Тепер ми можемо застосувати обернену теорію функцій з попереднього розділу до експоненціальної функції. З розділу 8.2 ми знаємо, що функція або$f(x) = b^x$ збільшується (якщо b > 1), або зменшується (якщо 0 < b < 1), і тому є один до одного. Отже, f має обернену функцію$f^{−1}$.

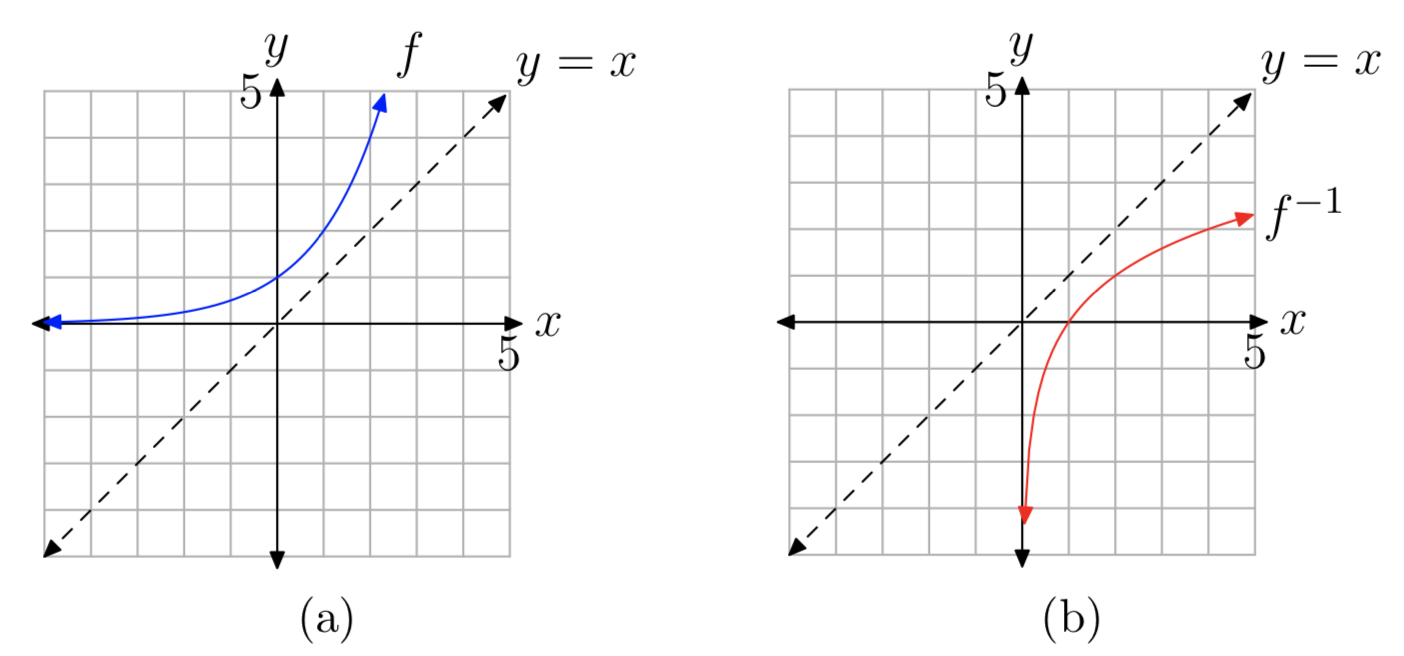
Як приклад розглянемо експоненціальну функцію$f(x) = 2^x$. f збільшується, має домен$D_{f} = (−\infty, \infty)$ і діапазон$R_{f} = (0, \infty)$. Її графік показаний на малюнку 1 (а). Графік оберненої функції$f^{−1}$ є відображенням графіка f поперек лінії y = x, і показаний на малюнку 1 (б). Оскільки домени та діапазони поміняються місцями, область зворотної функції є,$D_{f^{−1}} = (0, \infty)$ а діапазон є$R_{f^{−1}} = (−\infty, \infty)$.

Малюнок 1. Графіки$f(x) = 2^x$ та його$f^{−1}(x)$ зворотні є відображеннями по лінії y = x.

На жаль, коли ми намагаємося використовувати процедуру, наведену в розділі 8.4, щоб знайти формулу для$f^{−1}$, ми стикаємося з проблемою. Починаючи з$y = 2^x$, ми потім обмінюємося х і у, щоб отримати$x = 2^y$. Але тепер у нас немає алгебраїчного методу для вирішення цього останнього рівняння для y. Звідси випливає, що обернене не$f(x) = 2^x$ має формули, що включає звичайні арифметичні операції та функції, з якими ми знайомі. Таким чином, обернена функція є новою функцією. Ім'я цієї нової функції - логарифм від х до основи 2, і це позначається$f^{−1}(x) = log_{2}(x)$.

Нагадаємо, що визначальний зв'язок між функцією та її оберненою (Властивість 14 в розділі 8.4) просто говорить про те, що входи та виходи двох функцій взаємозамінні. Таким чином, зв'язок між$2^x$ і його зворотним$log_{2}(x)$ набуває такого вигляду:

$v = log_{2}(u) \longleftrightarrow u = 2^v$

Більш загально, для кожної експоненціальної функції$f(x) = b^x$ (b > 0,$b \ne 1$) обернена функція$f^{−1}(x)$ називається логарифмом від x до основи b, і позначається символом$log_{b}(x)$. Визначальне співвідношення дано в наступному визначенні.

Визначення$\PageIndex{1}$

Якщо b > 0 і$b \ne 1$, то логарифм від u до основи b визначається співвідношенням

$v = log_{b}(u) \longleftrightarrow u = b^v$. (2)

Для того щоб краще зрозуміти функцію логарифма, давайте попрацюємо кілька простих прикладів.

Приклад$\PageIndex{3}$

Обчислити$log_{2}(8)$.

Відповідь

Позначте необхідне значення по v, так$v = log_{2}(8)$. Потім по (2), використовуючи b = 2 і u = 8, випливає$2^v = 8$, що, а значить v = 3 (рішення шляхом огляду).

В останньому прикладі зверніть увагу, що$log_{2}(8) = 3$ is the exponent v такий, що$2^v = 8$. Таким чином, загалом, одним із способів інтерпретації визначення логарифма в (2)$log_{b}(u)$ є те, що$b^v = u$. показник v такий, що Іншими словами, значення логарифма є показником!

Приклад$\PageIndex{4}$

Обчислити$log_{10}(10000)$.

Відповідь

Знову ж таки, позначте потрібне значення по v, так$v = log_{10}(10000)$. За (2) випливає$10^v = 10 000$, що, а значить v = 4. Зауважте, що тут ми знову знайшли показник v = 4, який потрібен для бази 10, щоб отримати$10^v = 10 000$.

Приклад$\PageIndex{5}$

Обчислити$log_{3}(\frac{1}{9})$.

Відповідь

$v = log_{3}(\frac{1}{9})$

$\rightarrow 3^v = \frac{1}{9}$по (2)

$\rightarrow v = −2$так як$3^{−2} = \frac{1}{9}$

Приклад$\PageIndex{6}$

Вирішити рівняння$log_{5}(x) = 1$.

Відповідь

$log_{5}(x) = 1$

$\rightarrow 5^1 = x$по (2)

$\rightarrow x = 5$

Приклад$\PageIndex{7}$

Розв'яжіть рівняння$log_{b}(64) = 3$ для b.

Відповідь

$log_{b}(64) = 3$

$\rightarrow b^3 = 64$по (2)

$\rightarrow b = \sqrt[3]{64} = 4$

Приклад$\PageIndex{8}$

Вирішити рівняння$log_{\frac{1}{2}}(x) = −2$.

Відповідь

$log_{\frac{1}{2}}(x) = −2$

$\rightarrow (\frac{1}{2})^{−2} = x$по (2)

$\rightarrow \frac{1}{(\frac{1}{2})^2} = \frac{1}{\frac{1}{4}} = 4$

Співвідношення складу у власності 15 розділу 8.4, застосовані до$b^x$ і$log_{b}(x)$, стають

НЕРУХОМІСТЬ$\PageIndex{9}$

$$log_{b}(b^x) = x \label{10}$$

і

$$b^{log_{b}(x)} = x \label{11}.$$

Обидва рівняння важливі. Зауважте, що Equatio n\ ref {11} ag ain показує, що показник v такий, що$b^v = x$. Equatio n\ ref {10} буде часто використовуватися в цьому та пізніших розділах, щоб допомогти нам розв'язати експоненціальні рівняння.$log_{b}(x)$

Логарифмічні функції використовуються в багатьох областях науки і техніки. Наприклад, вони використовуються для визначення шкали Ріхтера для величин землетрусів, децибел шкали гучності звуку та астрономічної шкали для зоряної яскравості. Вони також є важливими інструментами для використання в обчисленні (як ми побачимо в розділі 8.8). Наше основне використання логарифмів у цьому підручнику полягатиме у вирішенні експоненціальних рівнянь, і тим самим допоможе нам вивчити фізичні явища, які описуються експоненціальними функціями (як у розділі 8.7).

Обчислення логарифмів

У прикладах 3 - 8 вище, ми змогли обчислити логарифми шляхом перетворення в експоненціальні рівняння, які можуть бути вирішені шляхом перевірки. Але легко помітити, що більшу частину часу це не спрацює. Наприклад, як би ми обчислили значення$log_{2}(7)$?

На щастя, математики знайшли інші методи обчислення логарифмів з високою точністю, і тепер їх можна легко наблизити за допомогою калькулятора або комп'ютера.

Ваш калькулятор має вбудовані кнопки для обчислення двох різних логарифмів,$log_{10}(x)$ і$log_{e}(x)$. $log_{10}(x)$називається загальним логарифмом, і$log_{e}(x)$ називається натуральним логарифмом.

Загальний логарифм: Загальний логарифм$log_{10}(x)$ обчислюється за допомогою LogButton на калькуляторі. Зверніть також увагу, що його зворотна функція$10^x$, може бути обчислена за допомогою тієї ж кнопки в поєднанні з 2-й кнопкою. Загальний логарифм, як правило, найзручніший для використання для обчислень, що включають наукові позначення (тому що ми використовуємо базову систему числення 10), і тому є логарифмом, який найчастіше використовується у фізичних науках. Через це, це часто просто скорочено log (x), і ми будемо робити це, а в решті частини тексту.

ЗАГАЛЬНИЙ ЛОГАРИФМ

log (x) і$log_{10}(x)$ є еквівалентними позначеннями. Таким чином, ми маємо визначальні відносини

$v = log(u) \longleftrightarrow u = 10^v$.

Властивості складу для загального логарифма

$log(10^x) = x$(12)

і

$10^{log(x)} = x$.

Природний логарифм: Натуральний логарифм\(log_{e}(x)\) is computed using the LNbutton on your calculator. Its inverse function, $e^x$ обчислюється за допомогою тієї ж кнопки у поєднанні з 2-ю кнопкою. Натуральний логарифм виявляється найзручнішим для використання в математиці, тому що безліч формул, особливо в численні, набагато простіше, коли використовується натуральний логарифм. Натуральний логарифм скорочено ln (x).

НАТУРАЛЬНИЙ ЛОГАРИФМ

ln (x) і$log_{e}(x)$ є еквівалентними позначеннями. Таким чином, ми маємо визначальні відносини

$v = ln(u) \longleftrightarrow u = e^v$.

Властивості складу для загального логарифма

$$ln(e^x) = x \label{13}$$

і

$$e^{\ln(x)} = x \lable{14}$$

Зверніть увагу, що при використанні калькулятора для обчислення журналу (x) та ln (x) ви зазвичай отримуєте лише приблизні значення, оскільки ці значення часто є ірраціональними числами.

А як щодо інших баз? Ви також можете обчислити їх на своєму калькуляторі, але спочатку нам потрібно буде розробити Змінити базову формулу в наступному розділі. Однак на цьому етапі ми можемо принаймні вирішити експоненціальні рівняння за участю основ 10 і e, як показано в наступних двох прикладах.

Приклад$\PageIndex{14}$

Вирішити рівняння$704 = 2(10)^{x}$.

Відповідь

Першим кроком є виділення експоненціальної з правого боку, розділивши обидві сторони на 2:

$352 = 10^x$

Потім просто застосуйте$log_{10}(x)$ функцію до обох сторін рівняння:

$log_{10}(352) = log_{10}(10^x)$

Але (10) означає, що$log_{10}(10^x) = x$. Тому$x = log_{10}(352) = log(352)$ є точним рішенням. Орієнтовна величина, за допомогою калькулятора, дорівнює 2.546542663 (див. Рис. Крім того, замість того, щоб взяти логарифм обох сторін на другому кроці, ви можете застосувати (2) до рівняння,$352 = 10^x$ щоб отримати$x = log_{10}(352)$.

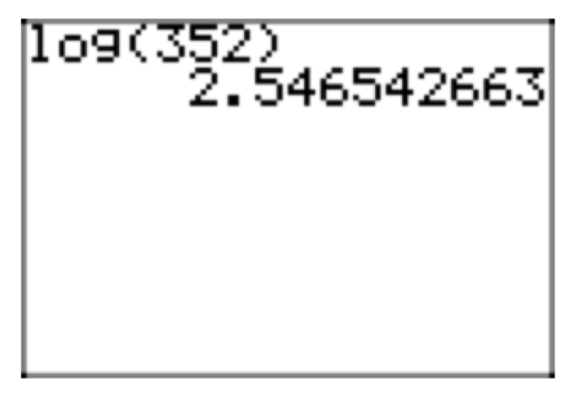
Малюнок 2. Наближення$log(352) = log_{10}(352)$.

Цей останній приклад показує, як логарифми можна використовувати для розв'язання експоненціальних рівнянь. Основна стратегія полягає в тому, щоб спочатку виділити експоненціальну з одного боку рівняння, а потім прийняти відповідні логарифми обох сторін. Ось ще один приклад на даний момент, а потім ми повернемося до цього процесу повторно в інших розділах, особливо коли ми працюємо з проблемами додатків.

Приклад$\PageIndex{15}$

Вирішити рівняння$30 = 20e^x$.

Відповідь

Спочатку виділіть експоненціальну з правого боку, розділивши обидві сторони на 20:

$1.5 = e^x$

Цього разу, оскільки основою експоненціальної функції є e, застосуйте функцію натурального логарифма до обох сторін:

$log_{e}(1.5) = log_{e}(e^x)$

Спростити праву сторону, так як$log_{e}(e^x) = x$ по (10):

$log_{e}(1.5) = x$

Тому$x = log_{e}(1.5) = ln(1.5)$ є точним рішенням. Приблизне значення, за допомогою калькулятора, становить 0,4054651081 (див. Рис.

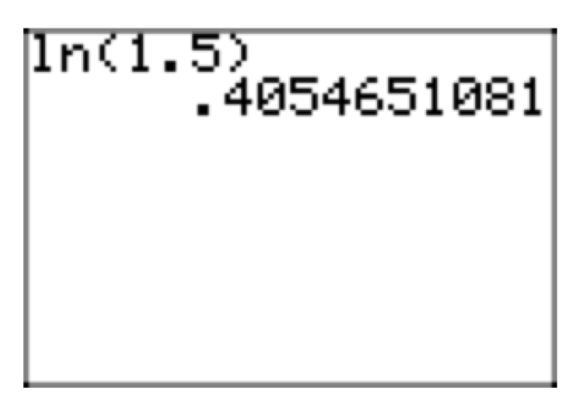
Малюнок 3. Наближення$ln1.5 = log_{e}(1.5)$.

У наступному розділі ми дізнаємося, як розв'язувати експоненціальні рівняння за участю інших основ.

Графіки логарифмічних функцій

На початку цього розділу ми розглянули графіки$f(x) = 2^x$ і його обернену функцію$f^{−1}(x) = log_{2}(x)$. Більш загально графік експоненціальної функції$f(x) = b^x$ для b > 1 показаний на малюнку 4 (а) разом з її оберненою логарифмічною функцією$f^{−1}(x) = log_{b}(x)$. Відповідно до розділу 8.4, два графіки є відображеннями через лінію y = x, аналогічно графіку для 0 < b < 1 показано на малюнку 4 (b).

Малюнок 4. Графіки$f(x) = b^x$ і$f^{−1}(x) = log_{b}(x)$ є відображеннями по лінії y = x.

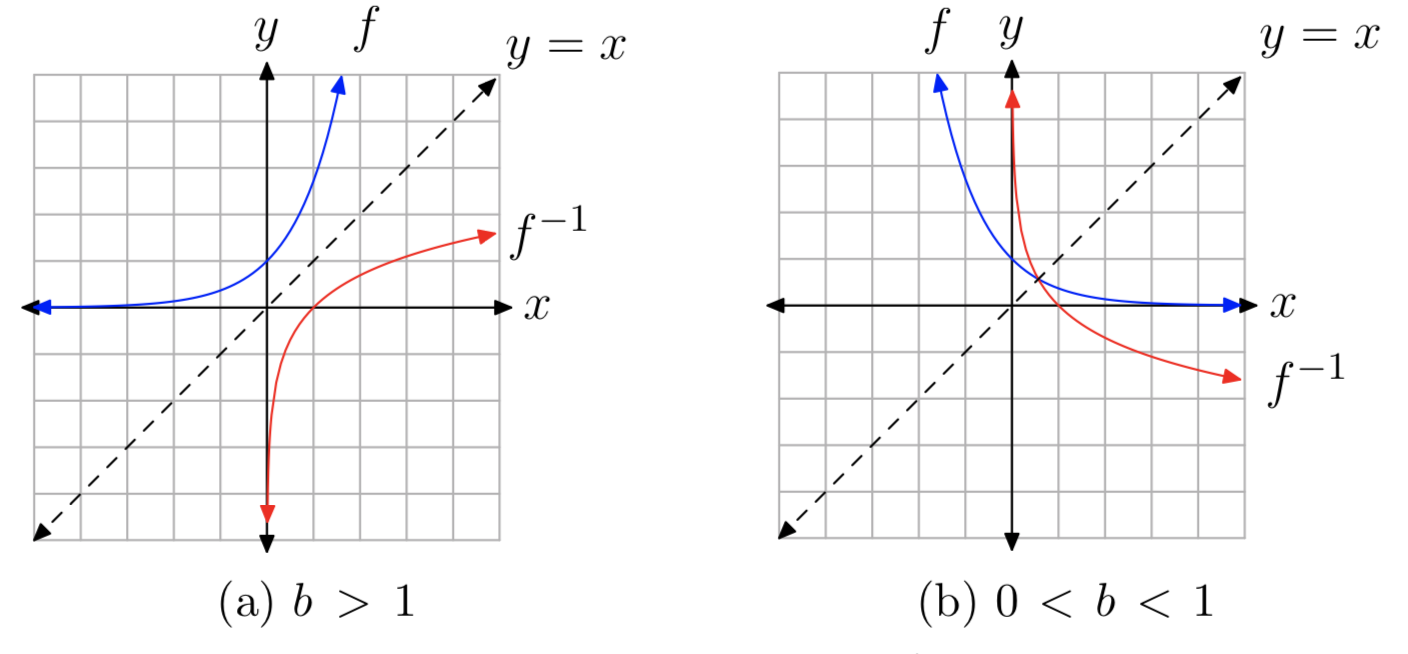
Оскільки домени та діапазони обернених функцій змінюються місцями, випливає, що

НЕРУХОМІСТЬ$\PageIndex{16}$

$Domain(log_{b}(x)) = (0, \infty)$

і

$Range(log_{b}(x)) = (−\infty, \infty)$.

Зокрема, зверніть увагу, що логарифм від'ємного числа, а також логарифм 0 не визначені.

Заслуговують на увагу дві конкретні точки на графіку логарифма. Так як$b^0 = 1$, випливає$log_{b}(1) = 0$, що, а значить і х -перехоплення графа$log_{b}(x)$ є (1, 0). Аналогічно$b^1 = b$, оскільки, випливає$log_{b}(b) = 1$, що, а значить (б, 1) знаходиться на графіку.

НЕРУХОМІСТЬ$\PageIndex{17}$

$log_{b}(1) = 0$

і

$log_{b}(b) = 1$

Нарешті, оскільки графік$b^x$ має горизонтальну асимптоту y = 0, графік$log_{b}(x)$ повинен мати вертикальну асимптоту x = 0. Така поведінка є наслідком того, що входи і виходи обернених функцій змінюються місцями, і може спостерігатися на малюнку 4.

У останньому прикладі нижче ми застосуємо перетворення до логарифму і подивимося, як це впливає на графік.

Приклад$\PageIndex{18}$

Побудуйте графік функції$f(x) = log_{2}(x+1)$.

Відповідь

Графік$f(x) = log_{2}(x+1)$ буде таким же, як і графік$g(x) = log_{2}(x)$ зрушеного на одну одиницю вліво. Графік g показаний на малюнку 1 (б). X-перехоплення (1, 0) на графіку g буде зміщено на одну одиницю вліво до (0,0) на графіку f Аналогічно вертикальна асимптота x = 0 на графіку g буде зрушена на одну одиницю вліво до лінії x = −1 на графіку f. Остаточний графік f показаний на малюнку 5.

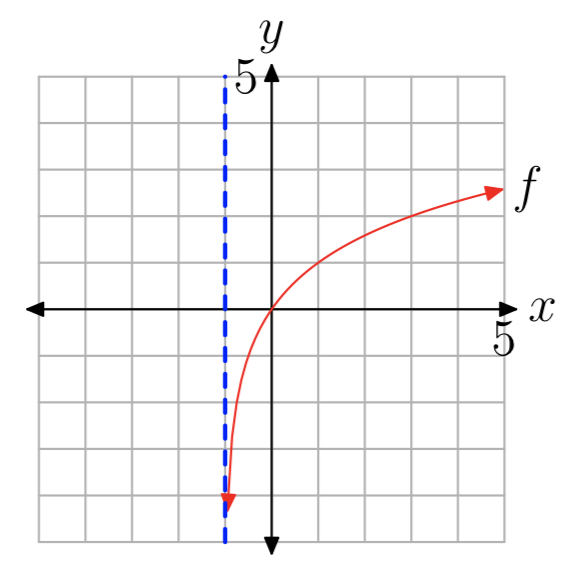
Малюнок 5. Графік$f(x) = log_{2}(x+1)$.

Вправа

У вправах 1 - 18 знайти точне значення функції при заданому значенні b.

Вправа$\PageIndex{1}$

$f(x) = log_{3}(x)$;$b = \sqrt[5]{3}$.

Відповідь

$\frac{1}{5}$

Вправа$\PageIndex{2}$

$f(x) = log_{5}(x)$; б = 3125.

Вправа$\PageIndex{3}$

$f(x) = log_{2}(x)$;$b = \frac{1}{16}$.

Відповідь

−4

Вправа$\PageIndex{4}$

$f(x) = log_{2}(x)$; б = 4.

Вправа$\PageIndex{5}$

$f(x) = log_{5}(x)$; б = 5.

Відповідь

1

Вправа$\PageIndex{6}$

$f(x) = log_{2}(x)$; б = 8.

Вправа$\PageIndex{7}$

$f(x) = log_{2}(x)$; б = 32.

Відповідь

5

Вправа$\PageIndex{8}$

$f(x) = log_{4}(x)$;$b = \frac{1}{16}$.

Вправа$\PageIndex{9}$

$f(x) = log_{5}(x)$;$b = \frac{1}{3125}$.

Відповідь

−5

Вправа$\PageIndex{10}$

$f(x) = log_{5}(x)$;$b = \frac{1}{25}$.

Вправа$\PageIndex{11}$

$f(x) = log_{5}(x)$;$b = \sqrt[6]{5}$.

Відповідь

$\frac{1}{6}$

Вправа$\PageIndex{12}$

$f(x) = log_{3}(x)$;$b = \sqrt[3]{3}$.

Вправа$\PageIndex{13}$

$f(x) = log_{6}(x)$;$b = \sqrt[6]{6}$.

Відповідь

$\frac{1}{6}$

Вправа$\PageIndex{14}$

$f(x) = log_{5}(x)$;$b = \sqrt[5]{5}$.

Вправа$\PageIndex{15}$

$f(x) = log_{2}(x)$;$b = \sqrt[6]{2}$.

Відповідь

$\frac{1}{6}$

Вправа$\PageIndex{16}$

$f(x) = log_{4}(x)$;$b = \frac{1}{4}$.

Вправа$\PageIndex{17}$

$f(x) = log_{3}(x)$;$b = \frac{1}{9}$.

Відповідь

−2

Вправа$\PageIndex{18}$

$f(x) = log_{4}(x)$; б = 64.

У вправах 19 - 26 скористайтеся калькулятором для оцінки функції при заданому значенні p Округліть відповідь до найближчої сотої.

Вправа$\PageIndex{19}$

ф (х) = лн (х); р = 10,06.

Відповідь

2. 31

Вправа$\PageIndex{20}$

ф (х) = лн (х); р = 9,87.

Вправа$\PageIndex{21}$

ф (х) = лн (х); р = 2,40.

Відповідь

0,88

Вправа$\PageIndex{22}$

ф (х) = лн (х); р = 9,30.

Вправа$\PageIndex{23}$

ф (х) = журнал (х); р = 7,68.

Відповідь

0,89

Вправа$\PageIndex{24}$

ф (х) = журнал (х); р = 652,22.

Вправа$\PageIndex{25}$

f (x) = журнал (х); р = 6,47.

Відповідь

0,81

Вправа$\PageIndex{26}$

ф (х) = журнал (х); р = 86,19.

У вправах 27 - 34 розв'яжіть задане рівняння, і округляйте свою відповідь до найближчих сотих.

Вправа$\PageIndex{27}$

$13 = e^{8x}$

Відповідь

0,32

Вправа$\PageIndex{28}$

$2 = 8e^{x}$

Вправа$\PageIndex{29}$

$19 = 10^{8x}$

Відповідь

0,16

Вправа$\PageIndex{30}$

$17 = 10^{2x}$

Вправа$\PageIndex{31}$

$7 = 6(10)^{x}$

Відповідь

0,07

Вправа$\PageIndex{32}$

$7 = e^{9x}$

Вправа$\PageIndex{33}$

$13 = 8e^{x}$

Відповідь

0,49

Вправа$\PageIndex{34}$

$5 = 7(10)^{x}$

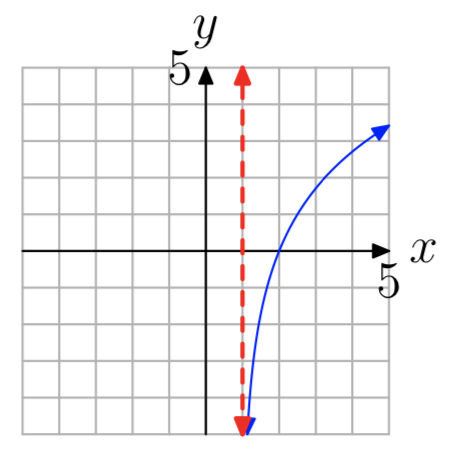
У вправах 35 - 42 показаний графік логарифмічної функції виду.$f(x) = log_{b}(x−a)$ Пропунктирна червона лінія являє собою вертикальну асимптоту. Визначте область функції. Висловіть свою відповідь в інтервальних позначеннях.

Вправа$\PageIndex{35}$

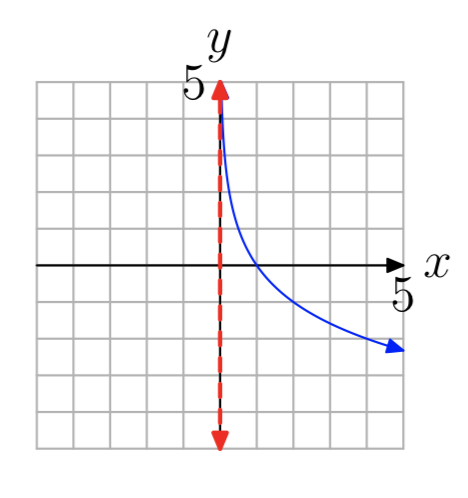
Відповідь

$(0, \infty)$

Вправа$\PageIndex{36}$

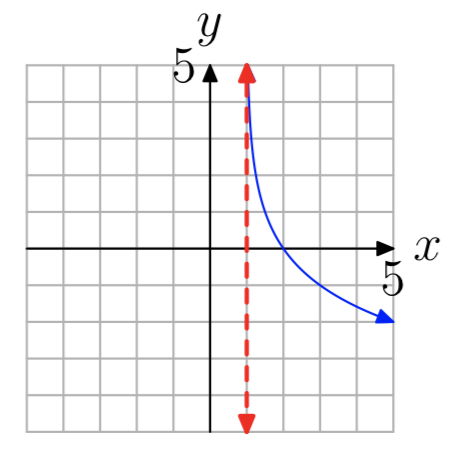
Вправа$\PageIndex{37}$

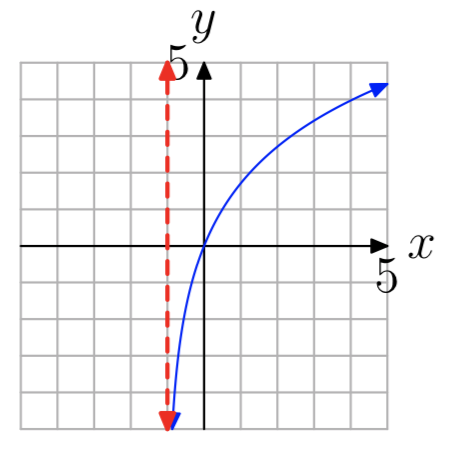
Відповідь

$(−1, \infty)$

Вправа$\PageIndex{38}$

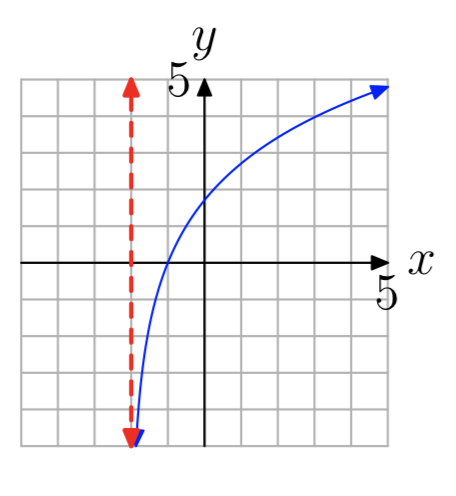
Вправа$\PageIndex{39}$

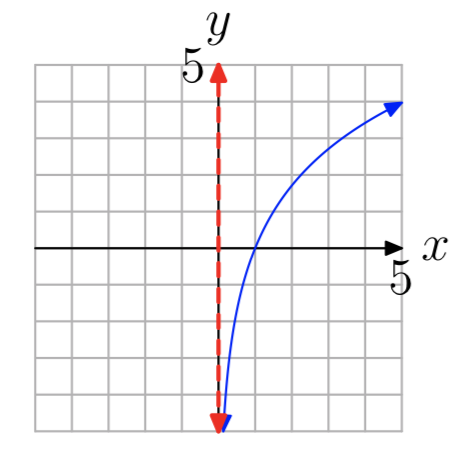
Відповідь

$(0, \infty)$

Вправа$\PageIndex{40}$

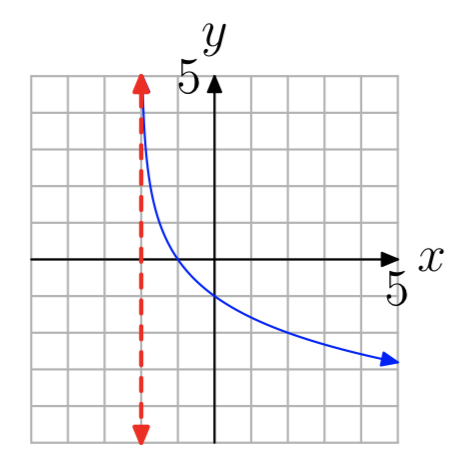
Вправа$\PageIndex{41}$

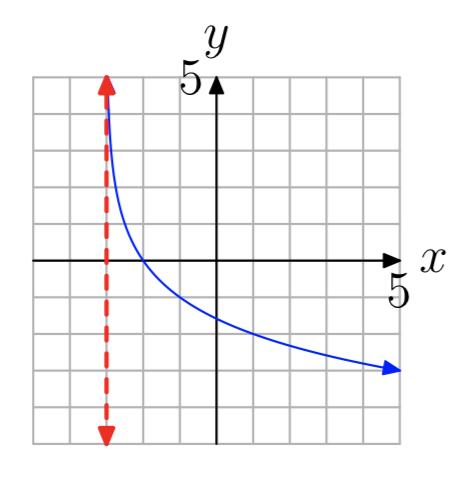
Відповідь

$(−3, \infty)$

Вправа$\PageIndex{42}$