8.3: Застосування експоненціальних функцій

Last updated
Save as PDF

Page ID: 58034

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У попередньому розділі ми розглянули проблему зростання населення, в якій населення щорічно зростало на фіксований відсоток. У такому випадку ми виявили, що популяція може бути описана експоненціальною функцією. Подібний аналіз покаже, що будь-який процес, в якому кількість зростає на фіксований відсоток щороку (або кожен день, годину тощо), може бути змодельований експоненціальною функцією. Складні відсотки - хороший приклад такого процесу.

Дискретні складні відсотки

Якщо ви поклали гроші на ощадний рахунок, то банк буде виплачувати вам відсотки (відсоток від залишку вашого рахунку) наприкінці кожного періоду часу, як правило, один місяць або один день. Наприклад, якщо часовий проміжок становить один місяць, цей процес називається щомісячним складанням. Термін складання відноситься до того, що відсотки додаються на ваш рахунок щомісяця, а потім в наступні місяці ви отримуєте відсотки на відсотки. Якщо часовий період становить один день, це називається щоденним складанням.

Давайте розглянемо щомісячне складання більш докладно. Припустимо, що ви вносите 100 доларів на свій рахунок, а банк виплачує відсотки за річною ставкою 5%. Нехай функція P (t) представляє суму грошей, яка у вас є на рахунку в момент t, де ми вимірюємо t в роках. Ми почнемо час при t = 0, коли початкова сума, яка називається основною, становить 100 доларів. Іншими словами, Р (0) = 100.

Під час наступного обговорення ми обчислимо залишок на рахунку наприкінці кожного місяця. Оскільки один місяць становить$\frac{1}{12}$ рік,$P(\frac{1}{12})$ являє собою залишок на кінець першого місяця,$P(\frac{2}{12})$ являє собою залишок на кінець другого місяця тощо.

В кінці першого місяця на залишок рахунку додаються відсотки. Так як річна процентна ставка 5%, то щомісячна процентна ставка становить$\frac{5%}{12}$, або$\frac{.05}{12}$ в десятковій формі. Хоча ми могли б$\frac{.05}{12}$ наблизити десятковим, корисніше, а також точніше буде залишити його в такому вигляді. Тому в кінці першого місяця зароблені відсотки будуть$100(\frac{.05}{12})$, тому загальна сума буде

$P(\frac{1}{12}) = 100+100(\frac{.05}{12}) =100(1+\frac{.05}{12})$. (1)

Тепер наприкінці другого місяця у вас буде сума, з якої ви розпочали цей місяць, а саме$P(\frac{1}{12})$, плюс ще місяць відсотків на цю суму. Тому загальна сума буде

$P(\frac{2}{12}) = P(\frac{1}{12})+P(\frac{1}{12})(\frac{.05}{12}) = P(\frac{1}{12})(1+\frac{.05}{12})$. (2)

Якщо замінити$P(\frac{1}{12})$ в рівнянні (2) на результат, знайдений в рівнянні (1), то

$P(\frac{2}{12})=100(1+\frac{.05}{12})(1+\frac{.05}{12}) = 100(1+ \frac{.05}{12})^2$. (3)

Давайте повторюємо ще один місяць. Наприкінці третього місяця у вас буде сума, з якої ви розпочали цей місяць$P(\frac{2}{12})$, а саме, плюс ще місяць відсотків на цю суму. Тому загальна сума буде

$P(\frac{3}{12}) = P(\frac{2}{12}) + P(\frac{2}{12})(\frac{.05}{12}) = P(\frac{2}{12})(1+\frac{.05}{12})$. (4)

Однак якщо замінити$P(\frac{2}{12})$ в рівнянні (4) на результат, знайдений в рівнянні (3), то

$P(\frac{3}{12}) = 100(1+\frac{.05}{12})^2(1+\frac{.05}{12}) = 100(1+\frac{.05}{12})^3$. (5)

Візерунок тепер повинен бути чітким. Сума грошей, яку ви будете мати на рахунку в кінці m місяців, задається функцією

$P(\frac{m}{12}) = 100(1+\frac{.05}{12})^m$.

Ми можемо переписати цю формулу через роки t,$\frac{m}{12}$ замінивши на t. тоді m = 12t, таким чином формула стає

$P(t) = 100(1+\frac{.05}{12})^{12t}$. (6)

Що було б інакше, якби ви почали з принципала 200? Простежуючи наші попередні кроки, повинно бути легко побачити, що нова формула буде

$P(t) = 200(1+\frac{.05}{12})^{12t}$.

Аналогічно, якби процентна ставка становила 4% на рік замість 5%, то ми б закінчили з формулою

$P(t) = 100(1+\frac{.04}{12})^{12t}$.

Таким чином, якщо ми дозволимо$P_{0}$ представляти основний, а r представляємо річну процентну ставку (в десятковій формі), то ми можемо узагальнити формулу до

$P(t) = P_{0}(1+\frac{r}{12})^{12t}$. (7)

Приклад$\PageIndex{8}$

Якщо основна сума становить 100 доларів, річна процентна ставка становить 5%, а відсотки збільшуються щомісяця, скільки грошей у вас буде через десять років?

У формулі (7), let$P_{0} = 100$, r = .05, а t = 10:

$P(10) = 100(1+\frac{.05}{12})^{12 \cdot 10}$

Ми можемо використовувати наш графічний калькулятор, щоб наблизити це рішення, як показано на малюнку 1.

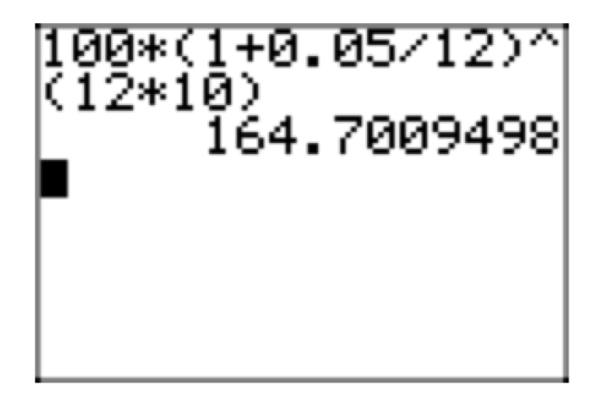
Знімок екрана 2019-07-26 в 4.43.50 PM.png — Малюнок 1. Обчислення суми після складання щомісяця протягом 10 років.

Таким чином, ви матимете $164.70 через десять років.

Приклад$\PageIndex{9}$

Якщо основна сума становить 10000 доларів, річна процентна ставка становить 5%, а відсотки збільшуються щомісяця, скільки грошей у вас буде через сорок років?

У формулі (7) нехай$P_{0} = 10000$, r =. 05, а т = 40:

$P(40) = 10000(1+\frac{.05}{12})^{12 \cdot 40} \approx 73584.17$

Таким чином, ви матимете $73 584,17 через сорок років.

Ці приклади ілюструють «чудо складного інтересу». В останньому прикладі ваш рахунок більше ніж у сім разів більший за оригінал, а загальний «прибуток» (сума отриманих відсотків) становить $63584,17. Порівняйте це з сумою, яку ви б отримали, якби ви знімали відсотки щомісяця (тобто без складання). У такому випадку ваша «прибуток» становила б лише 20000 доларів:

$years \cdot \frac{months}{year} \cdot \frac{interest}{month} = 40 \cdot 12 \cdot [(10000)(\frac{.05}{12})] =20000$

Велику різницю можна віднести до форми графіка функції P (t). Нагадаємо з попереднього розділу, що це експоненціальна функція зростання, так як вона стає більшою, графік в кінцевому підсумку буде круто підніматися. Таким чином, якщо ви зможете залишити свої гроші в банку досить довго, вони з часом різко зростуть.

А як щодо щоденного компаундування? Давайте знову проаналізуємо ситуацію, при якій основна сума становить 100 доларів, а річна процентна ставка - 5%. При цьому часовий проміжок, протягом якого виплачуються відсотки, становить один день, або$\frac{1}{365}$ рік, а денна процентна ставка дорівнює$\frac{5%}{365}$, або$\frac{.05}{365}$ в десятковій формі. Оскільки ми вимірюємо час у роках,$P(\frac{1}{365})$ представляє баланс на кінець першого дня,$P(\frac{2}{365})$ являє собою баланс на кінець другого дня і т.д. ми будемо виконувати ті ж дії, що і в попередньому аналізі для щомісячного складання.

В кінці першого дня у вас буде

$P(\frac{1}{365}) = 100+100(\frac{.05}{365}) = 100(1+\frac{.05}{365})$. (10)

Наприкінці другого дня у вас буде сума, з якої ви розпочали цей день$P(\frac{1}{365})$, а саме, плюс інший день на цю суму. Тому загальна сума буде

$P(\frac{2}{365}) = P(\frac{1}{365})+P(\frac{1}{365})(\frac{.05}{365}) = P(\frac{1}{365})(1+\frac{.05}{365})$. (11)

Якщо замінити$P(\frac{1}{365})$ в рівнянні (11) на результат, знайдений в рівнянні (10), то

$P(\frac{2}{365})=100(1+\frac{.05}{365})(1+\frac{.05}{365}) = 100(1+\frac{.05}{365}^2$. (12)

Наприкінці третього дня у вас буде сума, з якої ви почали цей день$P(\frac{2}{365})$, а саме, плюс інший день на цю суму. Тому загальна сума буде

$P(\frac{3}{365}) = P(\frac{2}{365})+P(\frac{2}{365})(\frac{.05}{365}) = P(\frac{2}{365})(1+\frac{.05}{365})$. (13)

Знову ж таки, заміна$P(\frac{2}{365})$ в рівнянні (13) результатом, знайденим у рівнянні (12), дає

$P(\frac{3}{365})=100(1+\frac{.05}{365})^{2}(1+\frac{.05}{365}) = 100(1+\frac{.05}{365})^3$. (14)

Продовження цієї закономірності показує, що сума грошей, яку ви будете мати на рахунку в кінці d днів, задається функцією.

$P(\frac{d}{365}) = 100(1+\frac{.05}{365})^d$.

Ми можемо переписати цю формулу через роки t,$\frac{d}{365}$ замінивши на t. тоді d = 365t, тому формула стає

$P(t) = 100(1+\frac{.05}{365})^{365t}$. (15)

Більш загально, якщо ви почали з основної суми$P_{0}$ та річної процентної ставки r (у десятковій формі), то формула буде

$P(t) = P_{0}(1+\frac{r}{365})^{365t}$. (16)

Порівнюючи формули (7) і (16) для щомісячного та щоденного складання, повинно бути очевидним, що єдина різниця полягає в тому, що в щомісячній формулі компаундирования використовується число 12, а число 365 використовується в щоденній формулі складання. Дивлячись на відповідний аналіз, показує, що це число виникає з частини року, за яку сплачуються відсотки ($\frac{1}{12}$у випадку щомісячного складання та$\frac{1}{365}$ у випадку щоденного складання). Таким чином, в кожному випадку це число (12 або 365) також дорівнює кількості разів, коли відсотки посилюються на рік. Звідси випливає, що якщо відсотки збільшуються щоквартально (кожні три місяці, або 4 рази на рік), формула буде такою

$P(t)=P_{0}(1+\frac{r}{4})^{4t}$.

Аналогічно, якщо відсотки посилюються щогодини (8760 разів на рік), формула буде

$P(t) = P_{0}(1+\frac{r}{8760})^{8760t}$.

Підводячи підсумки, маємо одне остаточне узагальнення:

ДИСКРЕТНИЙ СКЛАДНИЙ ІНТЕРЕС

Якщо$P_{0}$ основна сума, r - річна процентна ставка, а n - кількість разів, коли відсотки складаються на рік, то залишок на час t років дорівнює

$P(t) = P_{0}(1+\frac{r}{n})^{nt}$. (17)

Приклад$\PageIndex{18}$

Якщо основна сума становить 100 доларів, річна процентна ставка становить 5%, а відсотки складаються щодня, яким буде залишок через десять років?

У формулі (17) let$P_{0} = 100$, r = .05, n = 365, а t = 10:

$P(10) = 100(1+\frac{.05}{365})^{365 \cdot 10} \approx 164.87$

Таким чином, ви матимете $164.87 через десять років.

Приклад$\PageIndex{19}$

Якщо основна сума становить 10000 доларів, річна процентна ставка становить 5%, а відсотки складаються щодня, яким буде залишок через сорок років?

У формулі (17) нехай$P_{0} = 10000$, r = .05, n = 365, and t = 40:

$P(40) = 10000(1+\frac{.05}{365})^{365 \cdot 40} \approx 73880.44$

Таким чином, ви б мати $73880.44 через сорок років.

Як видно з порівняння прикладів 8 і 18 та прикладів 9 та 19, різниця між щомісячним та щоденним складанням, як правило, невелика. Однак різниця може бути суттєвою для великих принципалів та/або великих часових періодів.

Приклад$\PageIndex{20}$

Якщо основна сума становить 500 доларів, річна процентна ставка становить 8%, а відсотки збільшуються щоквартально, яким буде залишок через 42 місяці?

42 місяці це 3,5 року, так нехай$P_{0} = 500$, r =. 08, n = 4, а t = 3. 5 у формулі (17):

$P(3.5) = 500(1+\frac{.08}{4})^{4 \cdot 3.5} \approx 659.74$

Таким чином, ви матимете $659,74 через 42 місяці.

Безперервний складний відсоток і число e

Використовуючи формулу (17), просто розрахувати загальну суму для будь-якого типу компаундування. Хоча більшість банків складні відсотки або щодня, або щомісяця, це можна робити щогодини, або кожну хвилину, або кожну секунду тощо Що відбувається із загальною сумою, коли часовий період скорочується? Аналогічно, що відбувається, коли n збільшується у формулі (17)? У таблиці 1 наведена сума через рік з основною величиною$P_{0} = 100$, r = 0,05, і різними значеннями n:

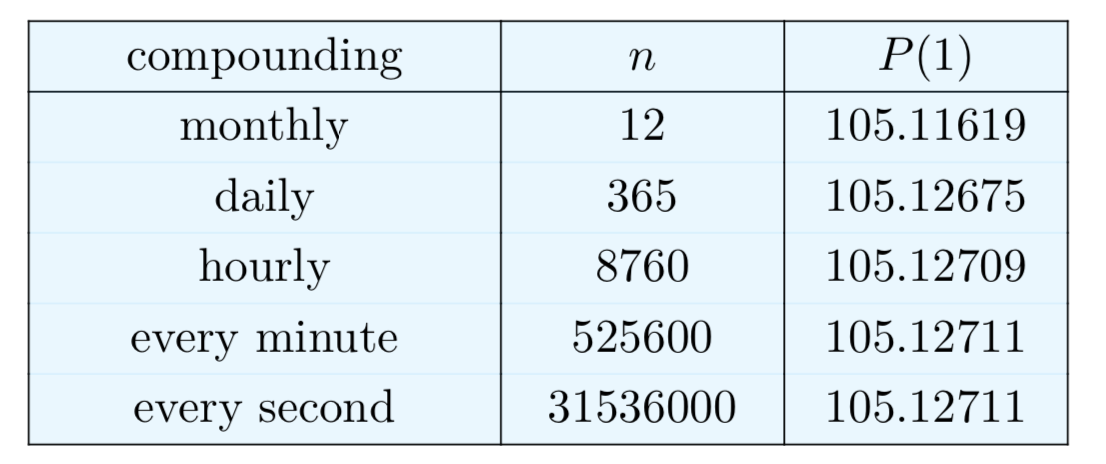
$Знімок екрана 2019-07-28 о 11.03.45 PM.png$

Таблиця 1. Порівняння дискретного компаундування з$P_{0} = 100$, r = .05, і t = 1 рік.

Навіть якщо ми проведемо наші обчислення до восьми цифр, виявляється, що суми в правій колонці таблиці 1 стабілізуються. Насправді, використовуючи обчислення, можна показати, що ці суми дійсно стають все ближче і ближче до конкретного числа, і ми можемо обчислити це число.

Починаючи з формули (17), ми дозволимо n підійти$\infty$. Іншими словами, ми дозволимо п отримати більше і більше без прив'язки, як ми почали робити в таблиці 1. Перший крок - використовувати Закони експонентів для написання

$P_{0}(1+\frac{r}{n})^{nt} = P_{0}[(1+\frac{r}{n})^{\frac{n}{r}}]^{rt}$

На наступному етапі замінюємо$frac{n}{r}$ на м. з того$\frac{n}{r} = m$, що випливає$\frac{r}{n} = \frac{1}{m}$, і у нас є

$P_{0}[(1+\frac{r}{n})^{\frac{n}{r}}]^{rt} = P_{0}[(1+\frac{1}{m})^{m}]^{rt}$

Тепер давайте підходимо$\infty$. Так як$m = \frac{n}{r}$ і r закріплена, то випливає, що m теж підходить$\infty$. Ми можемо використовувати функцію TABLE графічного калькулятора для дослідження збіжності виразу в дужках, коли m наближається до нескінченності.

Завантажте$(1+\frac{1}{m})^m$ в меню Y= графічного калькулятора, як показано на малюнку 2 (a). Звичайно, ви повинні використовувати x замість m і ввести (1+1/X) ^X.
Використовуйте TBLSET і встановіть Indepnt на Запитати, виберіть ТАБЛИЦЯ, а потім введіть цифри 10, 100,1000, 10000, 100000 та 100000, щоб отримати результат, показаний на малюнку 2 (b). Зверніть увагу, що (1+1/X) ^X схоже на число 2.7183. Якщо навести курсор на останній результат у стовпці Y1, ви можете побачити більш точність, 2.71828046932.

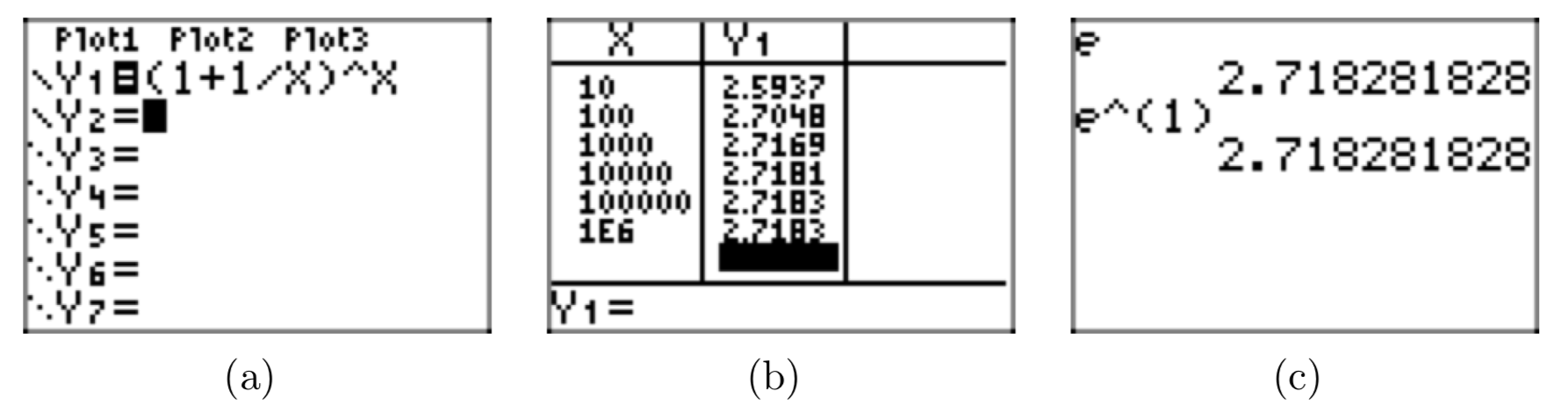
Знімок екрана 2019-08-06 в 2.31.04 PM.png — Малюнок 2. Ілюстрація зближення$(1 + \frac{1}{m})^m$ до е при збільшенні m до нескінченності

Зверніть увагу, що цифри у другому стовпці на малюнку 2 (b) здаються стабілізованими. Дійсно, за допомогою числення можна показати, що вираз в дужках вище стає все ближче і ближче до єдиного числа, яке називається e. Щоб уявити цю конвергенцію, пишемо

$1+\frac{1}{m})^m \rightarrow e$

e - ірраціональне число, приблизно 2.7183, як показано розрахунками на малюнку 2 (б). Звідси випливає, що

$P_{0}[(1+\frac{1}{m})^{m}]^{rt} \rightarrow P_{0}e^{rt}$

БЕЗПЕРЕРВНІ СКЛАДНІ ВІДСОТКИ

Якщо$P_{0}$ основна сума, r - річна процентна ставка, а відсотки складаються безперервно, то залишок на час t років дорівнює

$P(t) = P_{0}e^{rt}$

Перш ніж працювати з наступними прикладами, знайдіть на калькуляторі кнопки для числа e та для експоненціальної функції$e^x$. Набравши e або e^ (1) (за допомогою$e^x$ кнопки) дасть наближення до числа e, як показано на малюнку 2 (c). Порівняйте це наближення з тим, яке ви отримали раніше на малюнку 2 (б).

Приклад$\PageIndex{23}$

Якщо основна сума становить 100 доларів, річна процентна ставка становить 5%, а відсотки постійно посилюються, яким буде залишок через десять років？

У формулі (22) нехай$P_{0} = 100$, r = 0,05, а t = 10:

$P (10) = 100e^{(0.05)(10)}$

Скористайтеся калькулятором, щоб приблизити цей результат, як показано на малюнку 3.

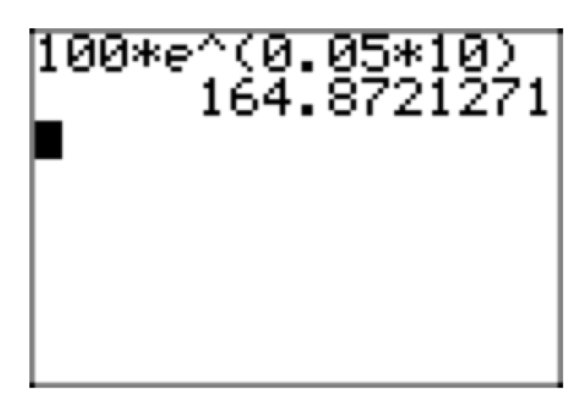
Знімок екрана 2019-08-06 в 2.42.49 PM.png — Малюнок 3. Обчислення суми після компаундирования безперервно протягом 10 років.

Таким чином, ви матимете $164.87 через десять років.

Приклад$\PageIndex{24}$

Якщо основна сума становить 10 000 доларів, річна процентна ставка становить 5%, а відсотки посилюються постійно, яким буде залишок через сорок років?

У формулі (22) нехай$P_{0} = 10000$, r = 0,05, а t = 40:

$P (10) = 10000e^{(0.05)(40)} \approx 73 890.56$

Таким чином, ви б мати $73 890.56 після сорока років.

Зверніть увагу, що формула безперервного компаундування (22) набагато простіша, ніж формула дискретного компаундування (17). Якщо принципал не дуже великий або період часу дуже довгий, попередні приклади показують, що безперервне складання також є близьким наближенням до щоденного складання. У прикладі 23 сума $164.87 така ж (округлена до найближчого цента), як сума для щоденного складання, знайдена в прикладі 18. При більшому основному та більш тривалому періоді часу сума $73 890.56 у прикладі 24 з використанням безперервного компаундування все ще лише приблизно на $10 більше, ніж сума $73 880.44 для щоденного складання, знайденого в прикладі 19.

ЗАУВАЖЕННЯ$\PageIndex{25}$

Число e може вразити вас як просто цікавість. Якщо так, то це було б великою помилкою. Число е насправді є одним з найважливіших чисел у математиці (це, мабуть, друге найвідоміше число, наступне π), і воно виникає природно як межа, описана в (21) вище. Використовуючи позначення з числення, пишемо

$lim_{m \rightarrow \infty} (1 +\frac{1}{m})^m = e \approx 2.71828$. (26)

Хоча в нашій дискусії вище цієї межі виникла в техногенному процесі, складному інтересі, він проявляється подібним чином у дослідженнях багатьох природних явищ. Деякі з цих додатків ми розглянемо пізніше в цьому розділі.

2. Так само експоненціальна функція ex є однією з найважливіших функцій, що використовуються в математиці, статистиці та багатьох галузях науки. З різних причин база e виявляється найбільш природною базою для використання для експоненціальної функції. Отже, функція$f(x) = e^x$ відома як природна експоненціальна функція.

Майбутня вартість і теперішня вартість

У цьому розділі ми вивели дві формули, одну для дискретних складних відсотків, а іншу для безперервних складних відсотків. Однак у прикладах, представлених до цих пір, ми використовували лише ці формули для обчислення майбутньої вартості: враховуючи основний P0 та процентну ставку r, скільки ви матимете на своєму рахунку за t років?

Інший тип питання, яке ми можемо вирішити, відомий як проблема поточної вартості: скільки грошей вам доведеться інвестувати під відсотки r, щоб мати Q доларів за t років? Ось кілька прикладів:

Приклад$\PageIndex{26}$

Скільки грошей вам доведеться інвестувати під 4% відсотків, що складаються щодня, щоб мати 8000 доларів за 6 років?

В даному випадку принципал$P_{0}$ невідомий, і підставляємо r = 0. 04, n = 365, а t = 6, в дискретну формулу компаундування (17). Оскільки P (6) = 8000, ми маємо рівняння

$8000 = P(6) = P_{0}(1+\frac{0.04}{365})^{(365)(5)}$

Це рівняння можна вирішити діленням:

$\frac{8000}{1+\frac{0.04}{365}} = P_{0}$

На малюнку 4 показано наближення калькулятора для цього результату.

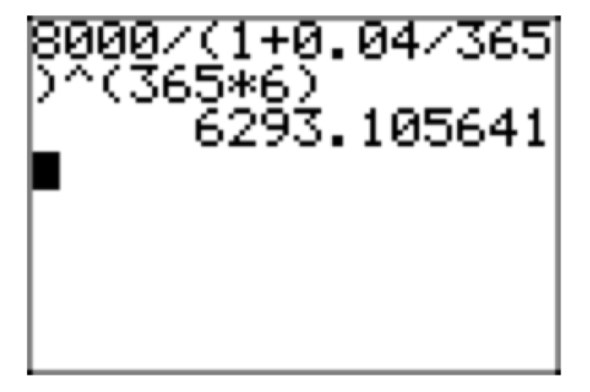
Знімок екрана 2019-08-06 в 2.54.34 PM.png — Малюнок 4. Нинішня вартість $8000, що складається щодня протягом шести років.

Таким чином, теперішнє значення приблизно$P_{0} \approx $6293.11$. Якщо ця сума інвестується зараз на 4% в сукупності щодня, то її майбутня вартість через 6 років складе $8000.

Приклад$\PageIndex{27}$

Скільки грошей вам доведеться інвестувати під 7% відсотків, що постійно посилюються, щоб мати $5000 доларів за 4 роки?

Як і в останньому прикладі, принципал$P_{0}$ невідомий, і на цей раз r = 0,07 і t = 4 у формулі безперервного складання (22). Тоді P (4) = 5000 дає рівняння

$5000 = P(4) = P_{0}e^{(0.07)(4)}$.

Як і в останньому прикладі, це рівняння також можна вирішити діленням:

$\frac{5000}{e^{(0.07)(4)}} = P_{0}$

Калькуляторне наближення для цього результату наведено на малюнку 5.

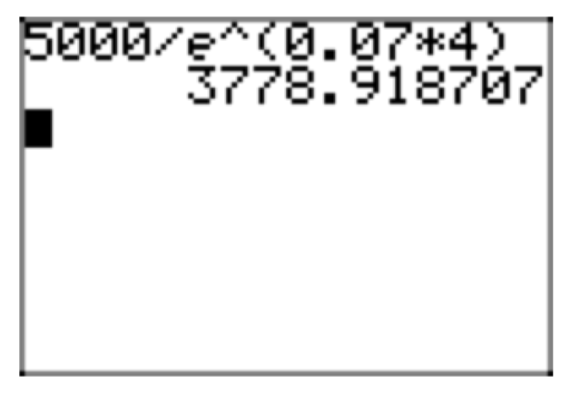
Знімок екрана 2019-08-06 в 2.58.30 PM.png — Малюнок 5. Нинішня вартість $5000, сумується безперервно протягом чотирьох років.

Таким чином, теперішнє значення приблизно$P_{0} \approx $3778.92$. Якщо ця сума інвестується зараз на 7%, що збільшується безперервно, то її майбутня вартість через 4 роки складе $5000.

Додаткові питання

Що стосується практичного застосування, існують також інші типи питань, які було б цікаво розглянути. Ось два приклади:

Якщо ви вносите 1000 доларів на рахунок, який сплачує 6% постійно, скільки часу вам знадобиться, щоб у вас на рахунку було 1500 доларів?
Якщо ви вносите 1000 доларів на рахунок, який сплачує 5% щомісяця, скільки часу знадобиться, щоб ваші гроші подвоїлися?

Давайте розглянемо перше питання (друге схоже). В даному випадку$P_{0} = 1000$ і r = 0,06. Вставивши ці значення в формулу безперервного компаундирования (22), отримаємо

$P(t) = 1000e^{0.06t}$.

Тепер ми хочемо, щоб майбутнє значення P (t) рахунку в якийсь час t дорівнювало $1500.

Тому ми повинні вирішити рівняння

$1500 = 1000e^{0.06t}$.

Однак тепер у нас є проблема, тому що змінна t знаходиться в експоненті виразу в правій частині рівняння. Хоча ми могли б наблизити рішення графічно, в даний час у нас немає алгебраїчного методу для вирішення такого рівняння, як це, де змінна знаходиться в експоненті (ці типи рівнянь називаються експоненціальними рівняннями). Протягом наступних кількох розділів ми визначимо інший тип функції, функцію логарифму, яка, в свою чергу, надасть нам метод розв'язання експоненціальних рівнянь. Потім ми повернемося до цих питань, а також обговоримо додаткові заявки.

Вправа

Вправа$\PageIndex{1}$

Припустимо, що ви інвестуєте 15 000 доларів під 7% відсотків, що складаються щомісяця. Скільки грошей буде на вашому рахунку через 4 роки? Округлите відповідь до найближчого цента.

Відповідь: $19830. 81

Вправа$\PageIndex{2}$

Припустимо, що ви інвестуєте 14 000 доларів під 3% відсотків, що складаються щомісяця. Скільки грошей буде на вашому рахунку через 7 років? Округлите відповідь до найближчого цента.

Вправа$\PageIndex{3}$

Припустимо, що ви інвестуєте 14 000 доларів під 4% відсотків, що складаються щодня. Скільки грошей буде на вашому рахунку через 6 років? Округлите відповідь до найближчого цента.

Відповідь: $17797. 25

Вправа$\PageIndex{4}$

Припустимо, що ви інвестуєте 15 000 доларів під 8% відсотків, що складаються щомісяця. Скільки грошей буде на вашому рахунку через 8 років? Округлите відповідь до найближчого цента.

Вправа$\PageIndex{5}$

Припустимо, що ви інвестуєте $4,000 під 3% відсотків, що складаються щомісяця. Скільки грошей буде на вашому рахунку через 7 років? Округлите відповідь до найближчого цента.

Відповідь: $4933. 42

Вправа$\PageIndex{6}$

Припустимо, що ви інвестуєте 3,000 доларів під 5% відсотків, що складаються щомісяця. Скільки грошей буде на вашому рахунку через 4 роки? Округлите відповідь до найближчого цента.

Вправа$\PageIndex{7}$

Припустимо, що ви інвестуєте 1,000 доларів під 3% відсотків, що складаються щомісяця. Скільки грошей буде на вашому рахунку через 4 роки? Округлите відповідь до найближчого цента.

Відповідь: $1127. 33

ФІЗИЧНІ ВПРАВИ$\PageIndex{8}$

Припустимо, що ви інвестуєте 19 000 доларів під 2% відсотків, що складаються щодня. Скільки грошей буде на вашому рахунку через 9 років? Округлите відповідь до найближчого цента.

Вправа$\PageIndex{9}$

Припустимо, що ви можете вкладати гроші під 4% відсотків, що складаються щомісяця. Скільки потрібно інвестувати, щоб мати 20 000 доларів за 2 роки? Округлите відповідь до найближчого цента.

Відповідь: $18464. 78

Вправа$\PageIndex{10}$

Припустимо, що ви можете вкладати гроші під 6% відсотків, що складаються щодня. Скільки потрібно інвестувати, щоб мати 1,000 доларів за 2 роки? Округлите відповідь до найближчого цента.

Вправа$\PageIndex{11}$

Припустимо, що ви можете вкладати гроші під 3% відсотків, що складаються щодня. Скільки потрібно інвестувати, щоб мати 20 000 доларів за 3 роки? Округлите відповідь до найближчого цента.

Відповідь: $18278. 69

Вправа$\PageIndex{12}$

Припустимо, що ви можете вкладати гроші під 3% відсотків, що складаються щомісяця. Скільки потрібно інвестувати, щоб мати 10 000 доларів за 7 років? Округлите відповідь до найближчого цента.

Вправа$\PageIndex{13}$

Припустимо, що ви можете вкладати гроші під 9% відсотків, що складаються щодня. Скільки потрібно інвестувати, щоб мати 4,000 доларів за 9 років? Округлите відповідь до найближчого цента.

Відповідь: $1779. 61

Вправа$\PageIndex{14}$

Припустимо, що ви можете вкладати гроші під 8% відсотків, що складаються щодня. Скільки потрібно інвестувати, щоб мати 18 000 доларів за 6 років? Округлите відповідь до найближчого цента.

Вправа$\PageIndex{15}$

Припустимо, що ви можете вкладати гроші під 8% відсотків, що складаються щодня. Скільки потрібно інвестувати, щоб мати 17 000 доларів за 6 років? Округлите відповідь до найближчого цента.

Відповідь: $10519. 87

Вправа$\PageIndex{16}$

Припустимо, що ви можете вкладати гроші під 9% відсотків, що складаються щодня. Скільки потрібно інвестувати, щоб мати $5,000 за 7 років? Округлите відповідь до найближчого цента.

У вправах 17 - 24 оцінюють функцію при заданому значенні p. Округлите відповідь до найближчої сотої.

Вправа$\PageIndex{17}$

$f(x) = e^x$; р = 1,57.

Відповідь: 4. 81

Вправа$\PageIndex{18}$

$f(x) = e^x$; р = 2,61.

Вправа$\PageIndex{19}$

$f(x) = e^x$; р = 3,07.

Відповідь: 21. 54

Вправа$\PageIndex{20}$

$f(x) = e^x$; р = −4,33.

Вправа$\PageIndex{21}$

$f(x) = e^x$; р = 1,42.

Відповідь: 4. 14

Вправа$\PageIndex{22}$

$f(x) = e^x$; р = −0,8.

Вправа$\PageIndex{23}$

$f(x) = e^x$; р = 4,75

Відповідь: 115. 58

Вправа$\PageIndex{24}$

$f(x) = e^x$; р = 3,60.

Вправа$\PageIndex{25}$

Припустимо, що ви інвестуєте 3,000 доларів під 4% відсотків, що постійно посилюються. Скільки грошей буде на вашому рахунку через 9 років? Округлите відповідь до найближчого цента.

Відповідь: $4299. 99

Вправа$\PageIndex{26}$

Припустимо, що ви інвестуєте 8,000 доларів під 8% відсотків, що постійно посилюються. Скільки грошей буде на вашому рахунку через 7 років? Округлите відповідь до найближчого цента.

Вправа$\PageIndex{27}$

Припустимо, що ви інвестуєте 1,000 доларів під 2% відсотків, що постійно посилюються. Скільки грошей буде на вашому рахунку через 3 роки? Округлите відповідь до найближчого цента.

Відповідь: $1061. 84

Вправа$\PageIndex{28}$

Припустимо, що ви інвестуєте 3,000 доларів під 8% відсотків, що постійно посилюються. Скільки грошей буде на вашому рахунку через 4 роки? Округлите відповідь до найближчого цента.

Вправа$\PageIndex{29}$

Припустимо, що ви інвестуєте 15 000 доларів під 2% відсотків, що постійно посилюються. Скільки грошей буде на вашому рахунку через 4 роки? Округлите відповідь до найближчого цента.

Відповідь: $16249. 31

Вправа$\PageIndex{30}$

Припустимо, що ви інвестуєте 8,000 доларів під 2% відсотків, що постійно посилюються. Скільки грошей буде на вашому рахунку через 6 років? Округлите відповідь до найближчого цента.

Вправа$\PageIndex{31}$

Припустимо, що ви інвестуєте 13 000 доларів під 9% відсотків, що постійно посилюються. Скільки грошей буде на вашому рахунку через 8 років? Округлите відповідь до найближчого цента.

Відповідь: $26707. 63

Вправа$\PageIndex{32}$

Припустимо, що ви інвестуєте 16 000 доларів під 4% відсотків, що постійно посилюються. Скільки грошей буде на вашому рахунку через 6 років? Округлите відповідь до найближчого цента.

Вправа$\PageIndex{33}$

Припустимо, що ви можете інвестувати гроші під 6% відсотків, що посилюються безперервно. Скільки потрібно інвестувати, щоб мати 17 000 доларів за 9 років? Округлите відповідь до найближчого цента.

Відповідь: $9906. 72

Вправа$\PageIndex{34}$

Припустимо, що ви можете інвестувати гроші під 8% відсотків, що посилюються безперервно. Скільки потрібно інвестувати, щоб мати $5,000 за 6 років? Округлите відповідь до найближчого цента.

Вправа$\PageIndex{35}$

Припустимо, що ви можете інвестувати гроші під 8% відсотків, що посилюються безперервно. Скільки потрібно інвестувати, щоб мати 10 000 доларів за 6 років? Округлите відповідь до найближчого цента.

Відповідь: $6187. 83

Вправа$\PageIndex{36}$

Припустимо, що ви можете інвестувати гроші під 6% відсотків, що посилюються безперервно. Скільки потрібно інвестувати, щоб мати 17 000 доларів за 13 років? Округлите відповідь до найближчого цента.

Вправа$\PageIndex{37}$

Припустимо, що ви можете інвестувати гроші під 2% відсотків, що посилюються безперервно. Скільки потрібно інвестувати, щоб мати 13 000 доларів за 8 років? Округлите відповідь до найближчого цента.

Відповідь: $11077. 87

Вправа$\PageIndex{38}$

Припустимо, що ви можете вкладати гроші під 9% відсотків, що посилюються безперервно. Скільки потрібно інвестувати, щоб мати 10 000 доларів за 15 років? Округлите відповідь до найближчого цента.

Вправа$\PageIndex{39}$

Припустимо, що ви можете інвестувати гроші під 7% відсотків, що посилюються безперервно. Скільки потрібно інвестувати, щоб мати 18 000 доларів за 10 років? Округлите відповідь до найближчого цента.

Відповідь: $8938. 54

Вправа$\PageIndex{40}$

Припустимо, що ви можете вкладати гроші під 9% відсотків, що посилюються безперервно. Скільки потрібно інвестувати, щоб мати 14 000 доларів за 12 років? Округлите відповідь до найближчого цента.