8.4: Зворотна функція
- Page ID
- 58048
Як ми бачили в останньому розділі, для вирішення прикладних задач, що включають експоненціальні функції, нам потрібно буде вміти вирішувати експоненціальні рівняння, такі як
\(1500 = 1000e^{0.06t}\)або\(300 = 2^x\).
Однак в даний час у нас немає жодних математичних інструментів для вирішення змінної, яка з'являється як показник, як у цих рівняннях. У цьому розділі ми розробимо поняття зворотної функції, яка, в свою чергу, буде використовуватися для визначення інструменту, який нам потрібен, логарифм, в розділі 8.5.
Функції «один-на-один»
Визначення\(\PageIndex{1}\)
Задана функція f вважається один до одного, якщо для кожного значення y в діапазоні f існує лише одне значення x в області f таке, що y = f (x). Іншими словами, f є один до одного, якщо кожен вихід y f відповідає точно одному входу x.
Найпростіше зрозуміти це визначення, подивившись на діаграми відображення і графіки деяких прикладів функцій.
Приклад\(\PageIndex{2}\)
Розглянемо дві функції h і k, визначені відповідно до діаграм відображення на малюнку 1. На малюнку 1 (a) є два значення в області, які обидва відображені на 3 в діапазоні. Значить, функція h не один до одного. З іншого боку, на малюнку 1 (b) для кожного виходу в діапазоні k є лише один вхід у домені, який відображається на ньому. Тому k - функція один-на-один.
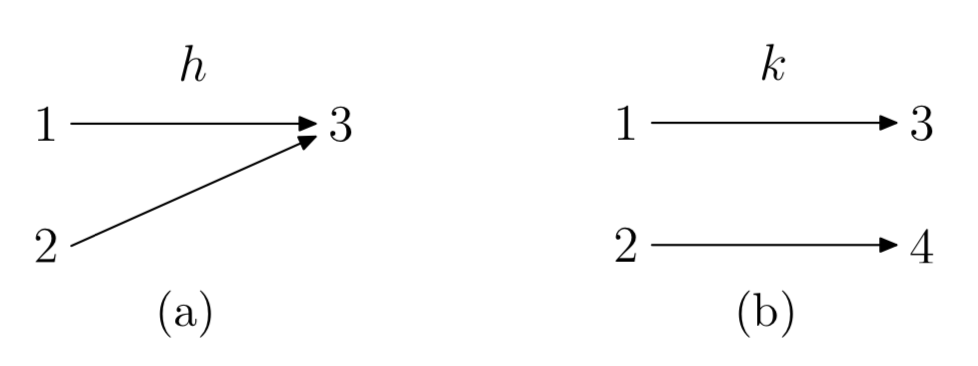
Приклад\(\PageIndex{3}\)
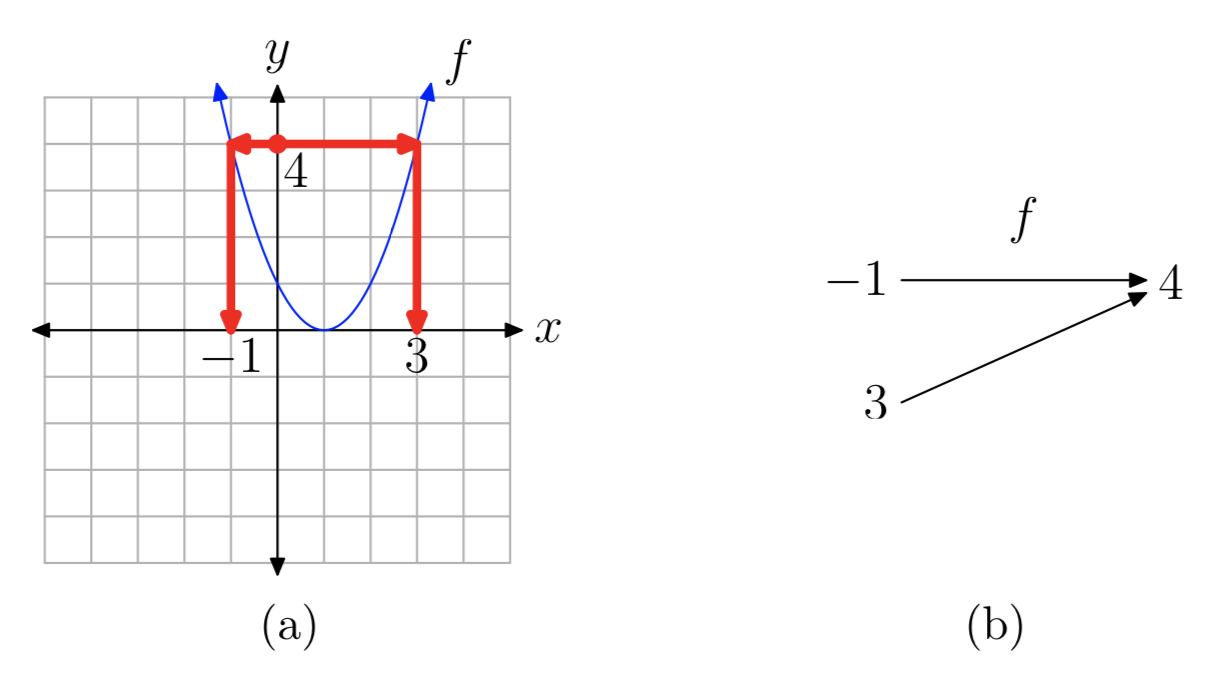
Графік функції показаний на малюнку 2 (а). Для цієї функції f значення y 4 є виходом, відповідним двом вхідним значенням, x = −1 і x = 3 (див. відповідну діаграму відображення на рис. 2 (b)). Тому f не один на один.
Графічно це видно шляхом малювання горизонтальних відрізків від точки (0, 4) на осі y до відповідних точок на графіку, а потім малювання вертикальних відрізків до осі x. Ці відрізки відповідають осі x на − 1 і 3.
Вправа\(\PageIndex{4}\)
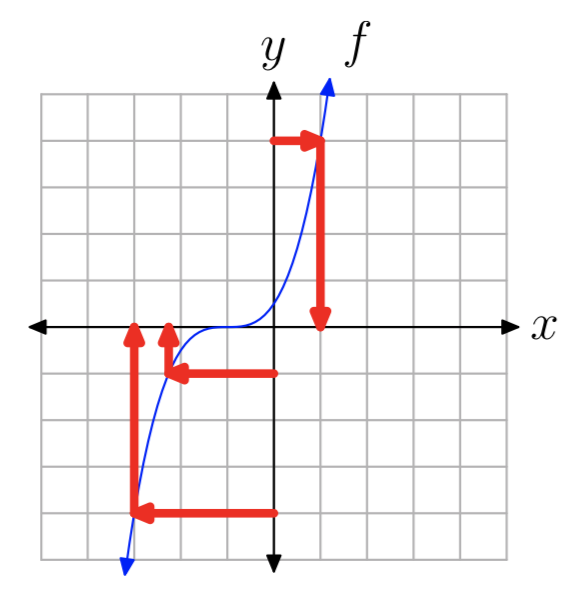
На малюнку 3 кожне значення y в діапазоні f відповідає лише одному вхідному значенню x, тому ця функція є один до одного.
Графічно це можна побачити, подумки намалювавши горизонтальний відрізок від кожної точки на осі Y до відповідної точки на графіку, а потім намалювавши вертикальний відрізок до осі x. Кілька прикладів наведено на малюнку 3. Очевидно, що ця процедура завжди призведе лише до однієї відповідної точки на осі x, оскільки кожне значення y відповідає лише одній точці на графіку. Насправді найпростіше просто відзначити, що оскільки кожна горизонтальна лінія перетинає графік лише один раз, то на кожен вихід може бути тільки один відповідний вхід.
Графічний процес, описаний у попередньому прикладі, відомий як тест горизонтальної лінії, забезпечує простий візуальний засіб визначення того, чи є функція один до одного.
ГОРИЗОНТАЛЬНА ЛІНІЯ ТЕСТ
Якщо кожна горизонтальна лінія перетинає графік f не більше одного разу, то f - один до одного. З іншого боку, якщо якась горизонтальна лінія перетинає графік f більше одного разу, то f не один до одного.
Зауваження 5. З тесту горизонтальної лінії випливає, що якщо f є строго зростаючою функцією, то f - один до одного. Так само кожна суворо зменшується функція також один до одного.
Обернені функції
Якщо f один до одного, то ми можемо визначити пов'язану функцію g, звану оберненою функцією f Ми дамо формальне визначення нижче, але основна ідея полягає в тому, що обернена функція g просто посилає виходи f назад на відповідні входи. Іншими словами, діаграма відображення для g виходить шляхом повороту стрілок на діаграмі відображення для f.
Приклад\(\PageIndex{6}\)
Функція f на рис. 4 (a) відображає 1 до 5 і 2 на −3. Отже, обернена функція g на рис. 4 (b) відображає виходи f назад на відповідні входи: від 5 до 1 та −3 до 2. Зауважте, що поворот стрілок на діаграмі відображення для f дає діаграму відображення для g.
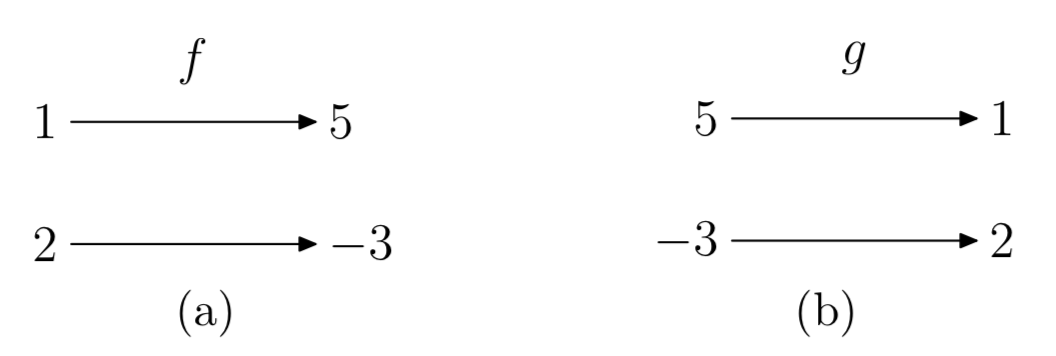
Оскільки зворотна функція g посилає виходи f назад на відповідні їм входи, то випливає, що входи g є виходами f, і навпаки. Таким чином, функції g і f пов'язані простим зміною між собою їх входів і виходів.
Початкова функція повинна бути один-на-один, щоб мати зворотну. Наприклад, розглянемо функцію h в прикладі 2. h не один до одного. Якщо ми повернемо стрілки на діаграмі відображення для h (див. Рис. 1 (а)), то отримане відношення не буде функцією, тому що 3 буде відображатися як 1, так і 2.
Перш ніж дати формальне визначення оберненої функції, корисно переглянути опис функції, наведену в розділі 2.1. Хоча функції часто визначаються за допомогою формули, пам'ятайте, що загалом функція - це лише правило, яке диктує, як пов'язати унікальне вихідне значення з кожним вхідним значенням.
Визначення\(\PageIndex{7}\)
Припустимо, що f є заданою функцією один до одного. Зворотна функція g визначається наступним чином: для кожного y в діапазоні f визначте g (y), щоб бути унікальним значенням x таким, що y = f (x).
Щоб зрозуміти це визначення, корисно подивитися на діаграму:
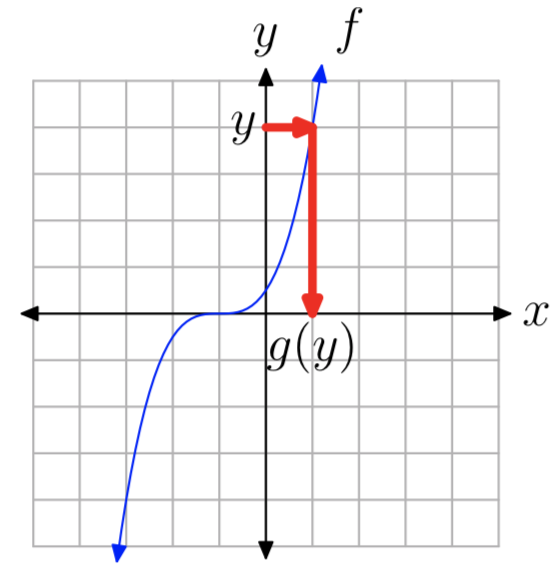
Вхідними даними для g є будь-яке значення y в діапазоні f, таким чином, вхідні дані на наведеній вище схемі є значенням на осі y. Вихід g - відповідне значення на осі x, яке задовольняє умові y = f (x). Зверніть увагу, зокрема, що значення x є унікальним, оскільки f є один до одного.
Зв'язок між початковою функцією f і її оберненою функцією g можна описати:
НЕРУХОМІСТЬ\(\PageIndex{8}\)
Якщо g - обернена функція f, то
\(x = g(y) \longleftrightarrow y = f(x)\).
Насправді це дійсно визначальна залежність для оберненої функції. Простий спосіб зрозуміти цей зв'язок (і всю концепцію зворотної функції) - це усвідомити, що він стверджує, що входи та виходи змінюються. Входи g - це виходи f, і навпаки. Звідси випливає, що домен і діапазон f і g змінюються місцями:
НЕРУХОМІСТЬ\(\PageIndex{9}\)
Якщо g - обернена функція f, то
Домен (g) = Діапазон (f) і Діапазон (g) = Домен (f).
Визначальний зв'язок у Property 8 також еквівалентний наступним двом ідентичностям, тому вони забезпечують альтернативну характеристику обернених функцій:
НЕРУХОМІСТЬ\(\PageIndex{10}\)
Якщо g - обернена функція f, то
g (f (x)) = x для кожного x у домені (f)
і
f (g (y)) = y для кожного y в Домені (g).
Зауважте, що перший оператор у Property 10 говорить, що g відображає висновок f (x) назад до вхідного x. Друге твердження говорить те ж саме з ролями f і g зворотного. Тому f і g повинні бути зворотними.
Властивість 10 також можна інтерпретувати так, щоб сказати, що функції g і f «скасовують» один одного. Якщо ми спочатку застосувати F до входу х, а потім застосувати г, ми отримаємо х назад знову. Так само, якщо ми застосуємо g до входу у, а потім застосувати f, ми отримуємо y назад знову. Таким чином, яку б дію не виконував, g змінює його, і навпаки.
Приклад\(\PageIndex{11}\)
Припустимо\(f(x) = x^3\). Таким чином, f - функція «кубірування». Яка операція призведе до зворотного процесу кубізації? Взяття кубового кореня. Таким чином, оберненою f повинна бути функція\(g(y) = \sqrt[3]{y}\).
Давайте перевіримо майно 10:
\(g(f(x))=g(x^3)= \sqrt[3]{x^3} = x\)
і
\(f(g(y)) = f(\sqrt[3]{y}) = (\sqrt[3]{y})^3 = y\)
Приклад\(\PageIndex{12}\)
Припустимо, f (x) = 4x−1. f діє на вхідний x, спочатку множивши на 4, а потім віднімаючи 1. Зворотна функція повинна перевернути процес: спочатку додати 1, а потім розділити на 4. Таким чином, зворотна функція повинна бути\(g(y) = \frac{y+1}{4}\).
Знову ж таки, давайте перевіримо властивість 10:
\(g(f(x)) = g(4x−1) = \frac{(4x−1)+1}{4} = \frac{4x}{4} = x\)
і
\(f(g(y)) = f(\frac{y+1}{4}) = 4(\frac{y+1}{4})−1 = (y+1)−1 = y\)
Зауваження 13.
- Обчислення g (f (x)), при якому вихід однієї функції використовується як вхід іншої, називається складом g з f Таким чином, обернені функції «скасовують» один одного в сенсі композиції. Склад функцій є важливим поняттям у багатьох областях математики, тому у вправах передбачено більше практики зі складом функцій.
- Якщо g є оберненою функцією f, то f також є оберненою g, що випливає з властивості 8 або Property 10. (Зверніть увагу, що мітки x і y для змінних не важливі. Ключова ідея полягає в тому, що дві функції є зворотними, якщо їх входи та виходи взаємозамінені.)
Позначення: Для того, щоб вказати, що дві функції f і g є зворотними, ми\(f^{−1}\) зазвичай використовуємо позначення\(f^{−1}\) для g. Крім того, щоб уникнути плутанини з типовими ролями x і y, часто корисно використовувати різні мітки для змінних. Переписуючи властивість 8 з\(f^{−1}\) позначеннями, і використовуючи нові мітки для змінних, ми маємо визначальну залежність:
НЕРУХОМІСТЬ\(\PageIndex{14}\)
\(v = f^{−1}(u) \longleftrightarrow u = f(v)\)
Аналогічно, переписуючи Property 10, ми маємо складові відносини:
НЕРУХОМІСТЬ\(\PageIndex{15}\)
\(f^{−1}(f(z))\)= z для кожного z в домені (f)
і
\(f(f^{−1}(z)) = z\)для кожного z в Домені (\(f^{−1}\))
Однак нове позначення має важливе попередження:
ПОПЕРЕДЖЕННЯ\(\PageIndex{16}\)
\(f^{−1}\)не означає\(\frac{1}{f}\)
Показник −1 є лише позначенням у цьому контексті. Застосовуючи до функції, вона означає зворотну функцію, а не зворотну функції.
Графік оберненої функції
Як складаються графіки f і\(f^{−1}\) пов'язані? Припустимо, що точка (a, b) знаходиться на графіку f Це означає, що b = f (a). Оскільки входи і виходи змінюються місцями для зворотної функції, то випливає\(a = f^{−1}(b)\), що, так (b, a) знаходиться на графіку\(f^{−1}\). Тепер (a, b) і (b, a) - це просто відображення один одного через лінію y = x (див. обговорення нижче для детального пояснення), тому випливає, що те ж саме вірно і з графами f і\(f^{−1}\) якщо ми графуємо обидві функції на одній системі координат (тобто як функції х).
Для прикладу розглянемо функції з Прикладу 11. Функції\(f(x) = x^3\) і\(f^{−1}(x) = \sqrt[3]{x}\) зображені на малюнку 6 разом з лінією y = x. кілька відображених пар точок також показані на графіку.
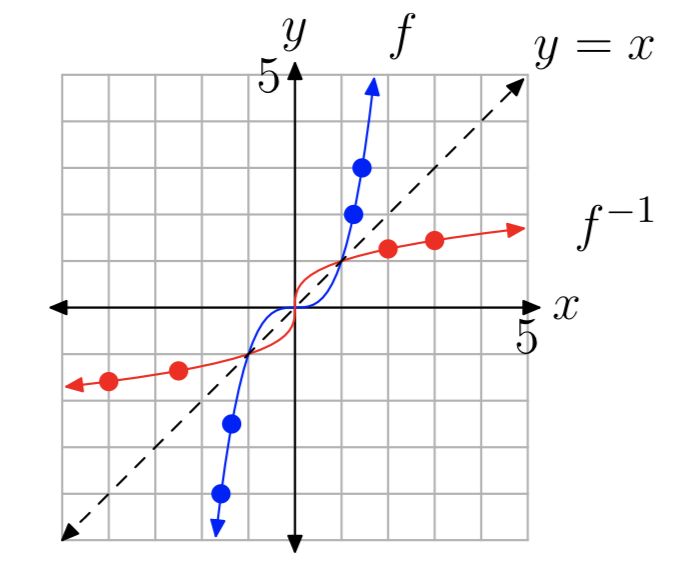
Щоб зрозуміти, чому точки (a, b) і (b, a) є лише відображеннями один одного через лінію y = x, розглянемо відрізок S між цими двома точками (див. Рис. Досить буде показати: (1) що S перпендикулярна прямій y = x, і (2) що точка перетину P відрізка S і лінії y = x рівновіддалена від кожного з (a, b) і (b, a).
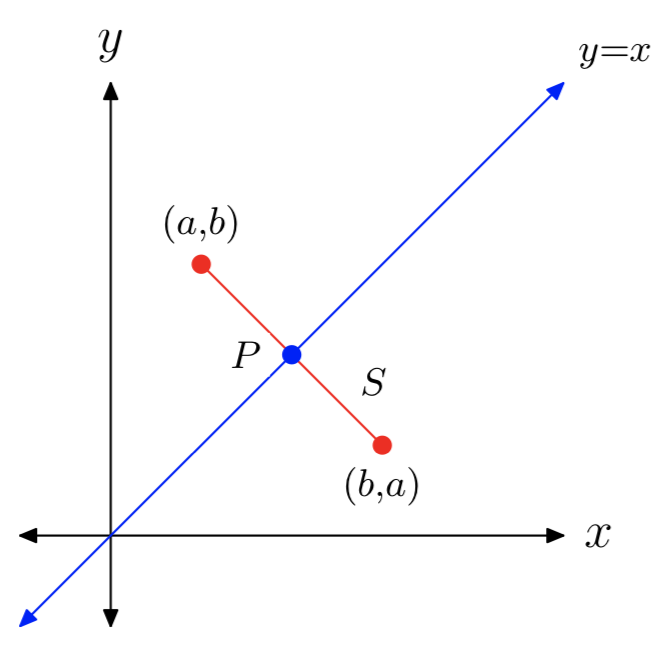
- Ухил S дорівнює
\(\frac{a−b}{b−a} = −1\),
а нахил лінії y = х дорівнює 1, тому вони перпендикулярні.
2. Рядок, що містить S, має рівняння y−b = − (x−a), або еквівалентно y = −x+ (a+b). Щоб знайти перетин S і прямої y = x, встановіть x = −x+ (a+b) і розв'яжіть для x, щоб отримати
\(x = \frac{a+b}{2}\).
Оскільки y = x, то випливає, що точка перетину
\(P = (\frac{a+b}{2}, \frac{a+b}{2})\)
Нарешті, ми можемо використовувати формулу відстані, представлену в розділі 9.6, для обчислення відстані від P до (a, b) та відстані від P до (b, a). В обох випадках обчислюється відстань виявляється
\(\frac{|a−b|}{\sqrt{2}}\)
Обчислення формули оберненої функції
Як знайти формулу оберненої функції? У прикладі 11 було легко побачити, що оберненою функцією «cubing» повинна бути функція кореня куба. Але як була отримана формула для зворотного в прикладі 12?
Власне, існує проста процедура знаходження формули для оберненої функції (за умови, що така формула існує; пам'ятайте, що не всі функції можна описати простою формулою, тому процедура для таких функцій не підійде). Наступна процедура працює, оскільки входи та виходи (змінні x та y) перемикаються на кроці 3.
ОБЧИСЛЕННЯ ФОРМУЛИ ОБЕРНЕНОЇ ФУНКЦІЇ
- Перевірте графік вихідної функції f (x), щоб побачити, чи проходить вона тест горизонтальної лінії. Якщо так, то f один-на-один і можна приступати.
- Запишіть формулу у вигляді xy-рівняння, як y = f (x).
- Обмін змінними x та y.
- Розв'яжіть нове рівняння для y, якщо це можливо. Результатом буде формула для\(f^{−1}(x)\).
Приклад\(\PageIndex{17}\)
Почнемо з пошуку зворотної функції f (x) = 4x−1 з прикладу 12.
Крок 1: Перевірка графіка показує, що f один до одного (див. Рис.
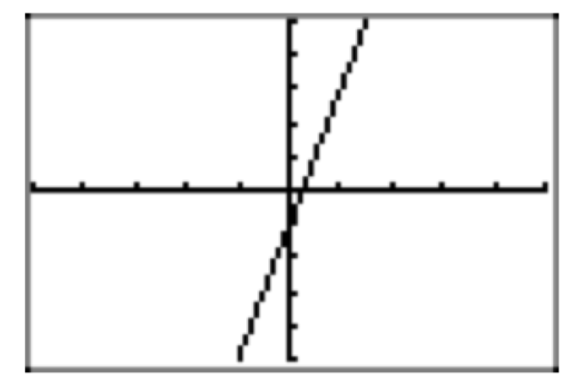
КРОК 2: Запишіть формулу у вигляді xy-рівняння: y = 4x − 1
КРОК 3: Обмін x та y: x = 4y − 1
КРОК 4: Вирішіть для y:
x = 4y − 1
\(\rightarrow x+1=4y\)
\(\rightarrow \frac{x+1}{4} = y\)
Таким чином,\(f^{−1}(x) = \frac{x+1}{4}\).
На малюнку 9 показано, що графік\(f^{−1}(x) = \frac{x+1}{4}\) є відображенням графіка f (x) = 4x−1 у рядку y = x. На цьому малюнку команда zSquare у меню ZOOM була використана для кращої ілюстрації відображення (команда zSquare вирівнює масштаби на обох осях).
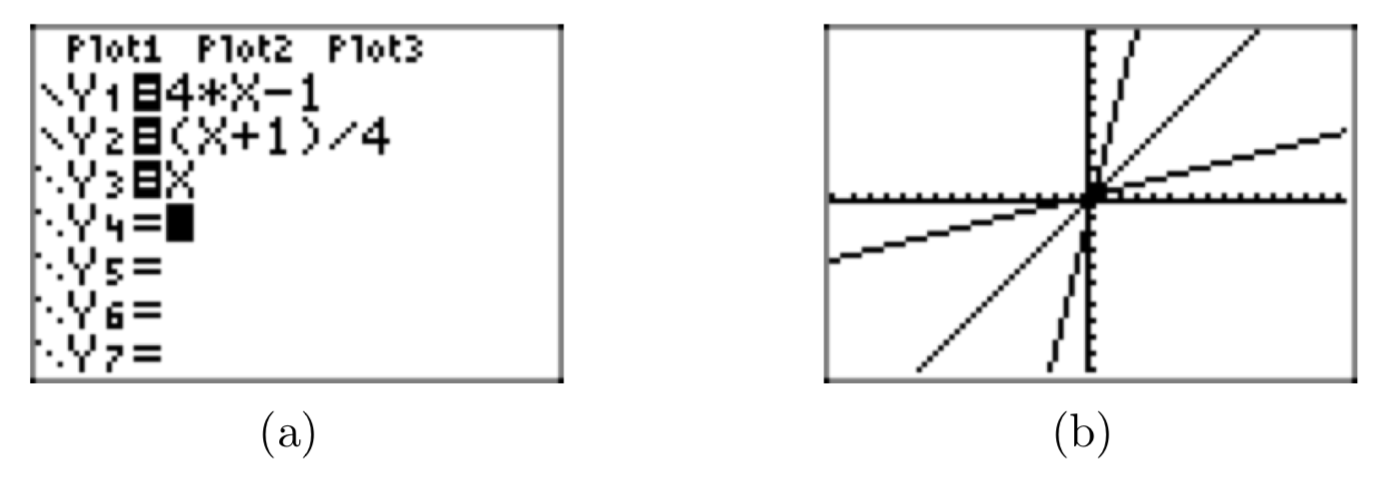
Приклад\(\PageIndex{18}\)
Цього разу ми знайдемо зворотне\(f(x) = 2x^5+3\).
Крок 1: Перевірка графіка показує, що f є один-на-один (це залишається для перевірки читача).
КРОК 2: Запишіть формулу у вигляді xy-рівняння:\(y = 2x^5+3\).
КРОК 3: Обмін x і y:\(x = 2y^5+3\).
КРОК 4: Вирішіть для y:
\(x = 2y^5+3\).
\(\rightarrow x−3 = 2y^5\)
\(\rightarrow \frac{x−3}{2} = y^5\)
\(\rightarrow \sqrt[5]{\frac{x−3}{2}} = y\)
Таким чином,\(f^{−1}(x) = \sqrt[5]{\frac{x−3}{2}}\)
Знову зверніть увагу, що графік\(f^{−1}(x) = \sqrt[5]{\frac{x−3}{2}}\) є відображенням графіка\(f(x) = 2x^5+3\) поперек лінії y = x (див. Рис.
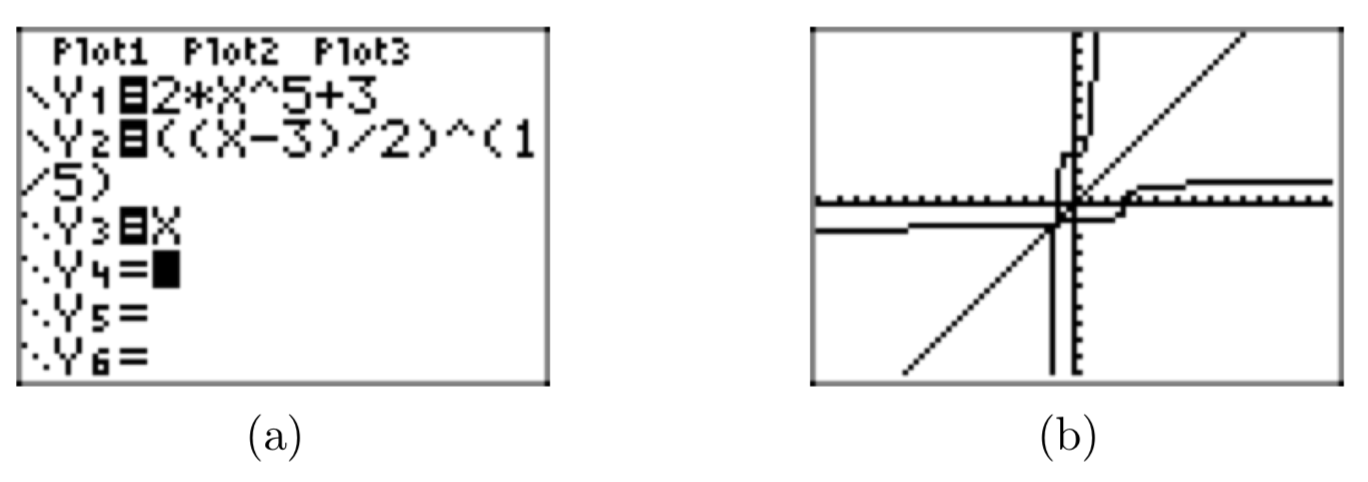
Приклад\(\PageIndex{19}\)
Знайдіть зворотне\(f(x) = \frac{5}{7+x}\).
Крок 1: Перевірка графіка показує, що f є один-на-один (це залишається для перевірки читача).
КРОК 2: Запишіть формулу у вигляді xy-рівняння:\(y = \frac{5}{7+x}\).
КРОК 3: Обмін x і y:\(x = \frac{5}{7+y}\).
КРОК 4: Вирішіть для y:
\(x = \frac{5}{7+y}\)
\(\rightarrow x(7+y) = 5\)
\(\rightarrow 7+y = \frac{5}{x}\)
\(y = \frac{5}{x}−7 = \frac{5 − 7x}{x}\)
Таким чином,\(f^{−1}(x) = \frac{5 − 7x}{x}\)
Приклад\(\PageIndex{20}\)
Цей приклад трохи складніший: знайдіть зворотну функцію\(f(x) = \frac{5x+2}{x−3}\).
Крок 1: Перевірка графіка показує, що f є один-на-один (це залишається для перевірки читача).
КРОК 2: Запишіть формулу у вигляді xy-рівняння:\(y = \frac{5x+2}{x−3}\).
КРОК 3: Обмін x і y:\(x = \frac{5y+2}{y−3}\).
КРОК 4: Вирішіть для y:
\(x = \frac{5y+2}{y−3}\)
\(\rightarrow x(y−3) = 5y+2\)
\(\rightarrow xy−3x = 5y+2\)
Це рівняння є лінійним у Виділяють члени, що містять змінну y з одного боку рівняння, коефіцієнт, потім ділять на коефіцієнт y.
\(xy−3x = 5y+2\)
\(xy−5y = 3x+2\)
\(y(x−5) = 3x+2\)
\(y = \frac{3x+2}{x−5}\)
Таким чином,\(f^{−1}(x) = \frac{3x+2}{x−5}\).
Приклад\(\PageIndex{21}\)
Відповідно до тесту горизонтальної лінії, функція\(h(x) = x^2\), звичайно, не один до одного. Однак, якщо ми розглядаємо лише праву половину або ліву половину функції (тобто обмежити домен\([0, \infty)\) або інтервалом або\((−\infty,0]\)), то функція буде один-на-один, і тому матиме зворотну (рис. 11 (а) показує ліву половину). Наприклад, припустимо, f є функцією\(f(x) = x^2\),\(x \le 0\)
У цьому випадку процедура все ще працює, за умови, що ми проводимо уздовж умови домену у всіх кроках, наступним чином:
Крок 1: Графік на малюнку 11 (а) проходить тест горизонтальної лінії, тому f є один до одного.
Крок 2: Запишіть формулу у формі xy-рівняння:\(y = x^2\),\(x \le 0\)
Крок 3: Обмін x і y:\(x = y^2\),\(y \le 0\)
Зверніть увагу, як x і y також повинні бути замінені в умовах домену.
Крок 4: Вирішіть для y:\(y = \pm \sqrt{x}\),\(y \le 0\)
Тепер є два варіанти для y, один позитивний і один негативний, але умова\(y \le 0\) говорить нам, що негативний вибір є правильним. Таким чином, останнє твердження рівнозначне
\(y = −\sqrt{x}\).
Таким чином,\(f^{−1}(x) = −\sqrt{x}\). Графік\(f^{−1}\) показаний на малюнку 11 (б), а графіки обох f і\(f^{−1}\) показані на малюнку 11 (c) у вигляді відображень по лінії y = x.
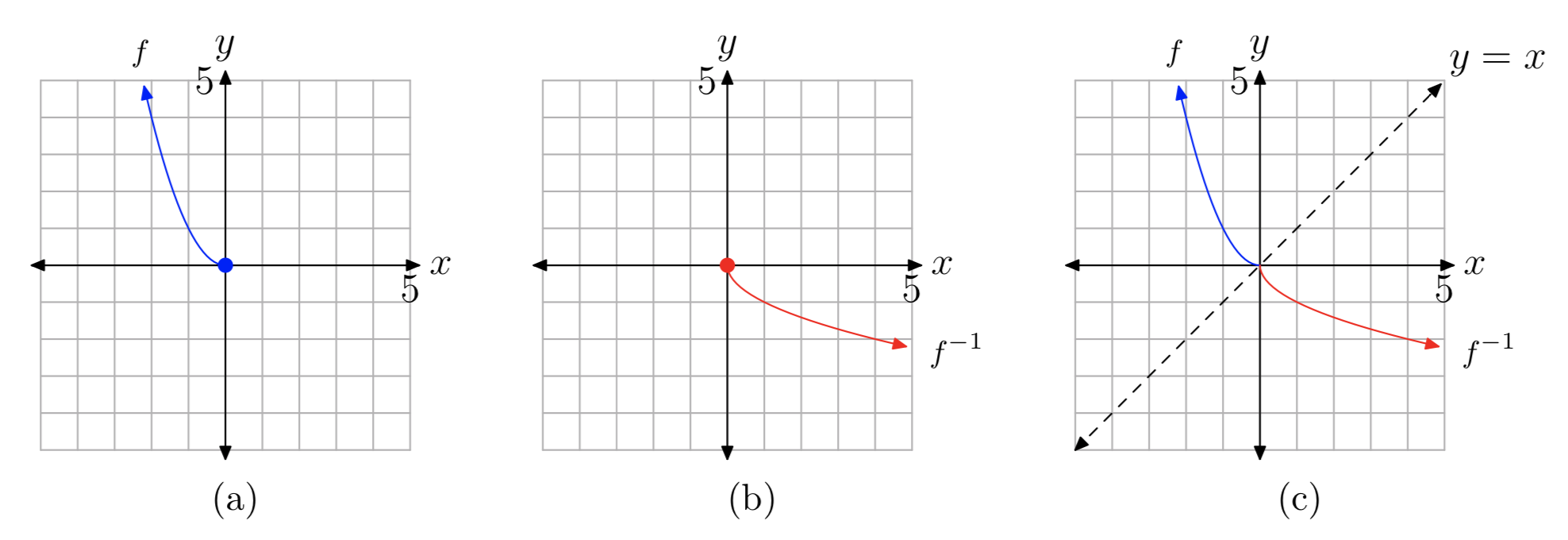
Вправа
У вправах 1 - 12 використовуйте графік, щоб визначити, чи є функція один-на-один.
Вправа\(\PageIndex{1}\)
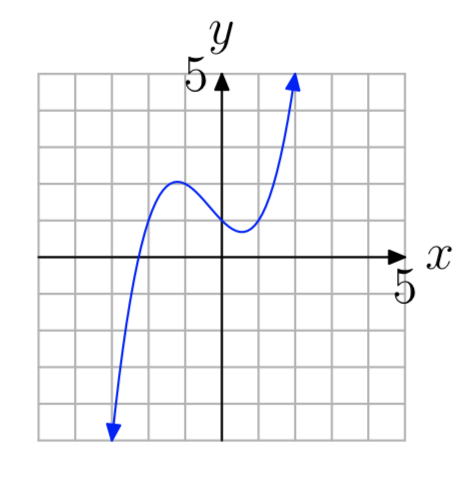
- Відповідь
-
не один на один
Вправа\(\PageIndex{2}\)
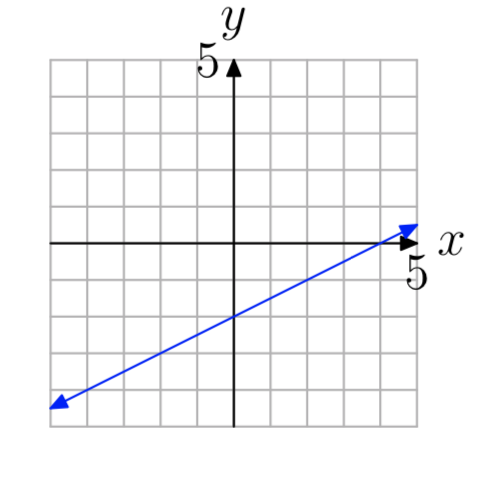
Вправа\(\PageIndex{3}\)
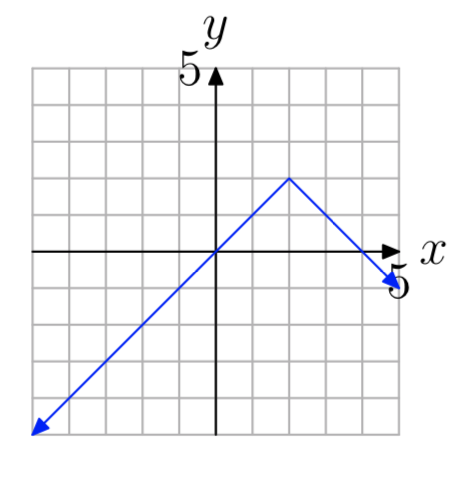
- Відповідь
-
не один на один
Вправа\(\PageIndex{4}\)
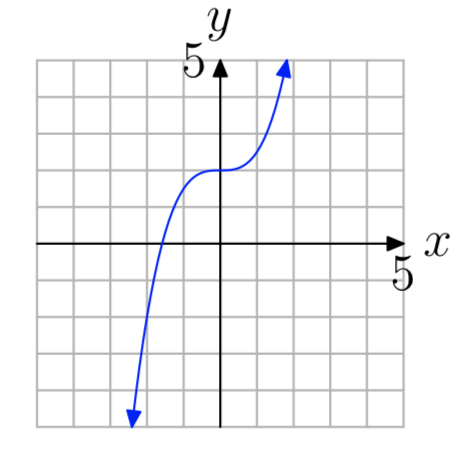
Вправа\(\PageIndex{5}\)
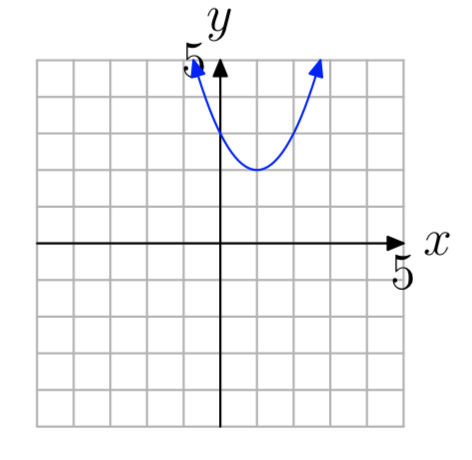
- Відповідь
-
не один на один
Вправа\(\PageIndex{6}\)
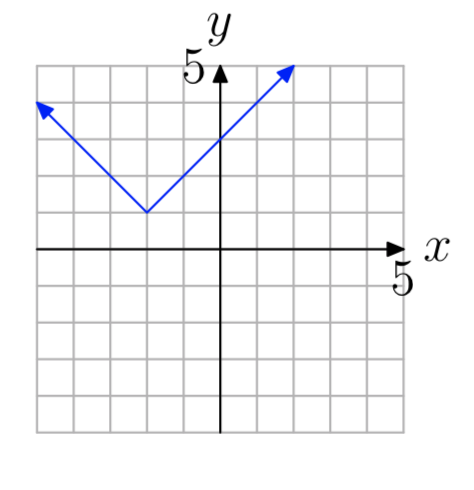
Вправа\(\PageIndex{7}\)
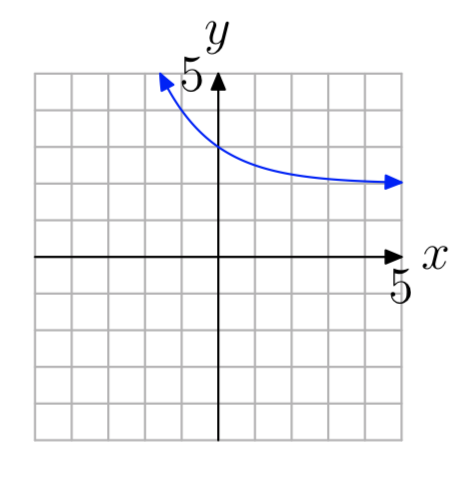
- Відповідь
-
один-на-один
Вправа\(\PageIndex{8}\)
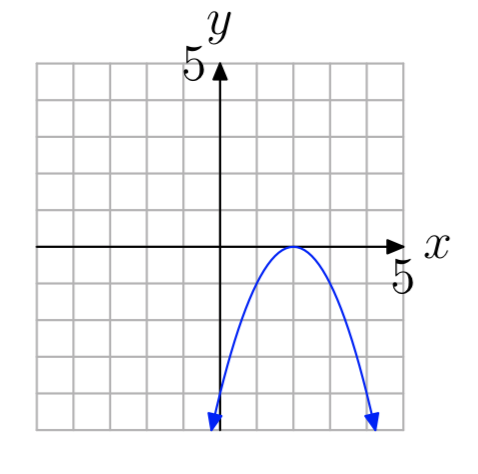
Вправа\(\PageIndex{9}\)
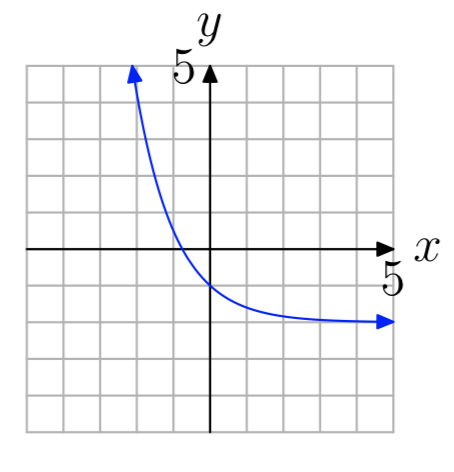
- Відповідь
-
один-на-один
Вправа\(\PageIndex{10}\)
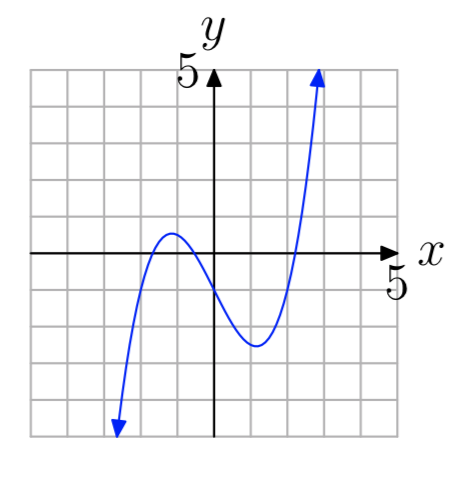
Вправа\(\PageIndex{11}\)
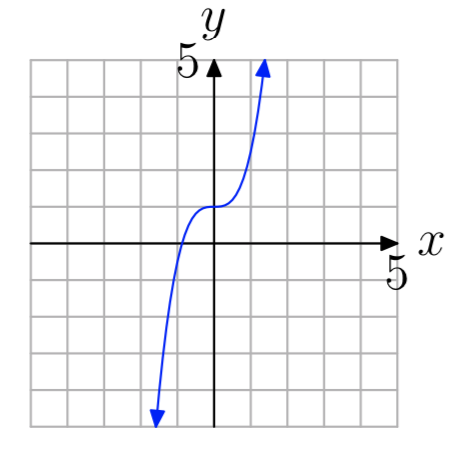
- Відповідь
-
один-на-один
Вправа\(\PageIndex{12}\)
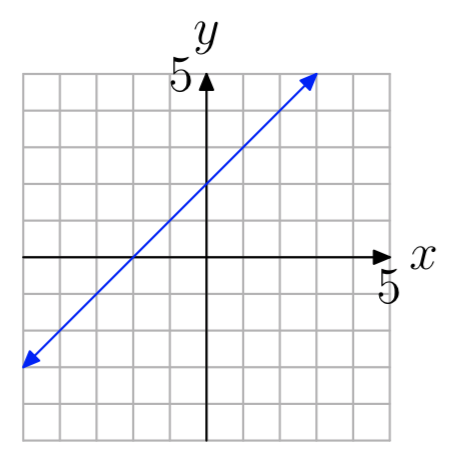
У вправах 13 - 28 оцініть склад g (f (x)) і спростіть свою відповідь.
Вправа\(\PageIndex{13}\)
\(g(x) = \frac{9}{x}\),\(f(x) = −2x^2+5x−2\)
- Відповідь
-
\(\frac{−9}{2x^2−5x+2}\)
Вправа\(\PageIndex{14}\)
\(f(x) = −\frac{5}{x}\),\(g(x) = −4x^2+x−1\)
Вправа\(\PageIndex{15}\)
\(g(x) = 2\sqrt{x}\),\(f(x)=−x−3\)
- Відповідь
-
\(2\sqrt{−x−3}\)
Вправа\(\PageIndex{16}\)
\(f(x) = 3x^2−3x−5\),\(g(x) = \frac{6}{x}\)
Вправа\(\PageIndex{17}\)
\(g(x) = 3\sqrt{x}\),\(f(x) = 4x+1\)
- Відповідь
-
\(3\sqrt{4x+1}\)
Вправа\(\PageIndex{18}\)
f (x) = −3х−5, г (х) =−х−2
Вправа\(\PageIndex{19}\)
\(g(x) = −5x^2+3x−4\),\(f(x) = \frac{5}{x}\)
- Відповідь
-
\(−\frac{125}{x^2}+\frac{15}{x}−4\)
Вправа\(\PageIndex{20}\)
г (х) = 3х+3,\(f(x) = 4x^2 −2x−2\)
Вправа\(\PageIndex{21}\)
\(g(x) = 6\sqrt{x}\), f (х) = −4х+4
- Відповідь
-
\(6\sqrt{−4x+4}\)
Вправа\(\PageIndex{22}\)
g (x) = 5x−3, f (x) =−2x−4
Вправа\(\PageIndex{23}\)
\(g(x) = 3\sqrt{x}\), f (х) = −2x+1
- Відповідь
-
\(3\sqrt{−2x+1}\)
Вправа\(\PageIndex{24}\)
\(g(x) = \frac{3}{x}\),\(f(x)=−5x^2−5x−4\)
Вправа\(\PageIndex{25}\)
\(f(x)=\frac{5}{x}\), g (x) =−х+1
- Відповідь
-
\(−\frac{5}{x}+1\)
Вправа\(\PageIndex{26}\)
\(f(x) = 4x^2+3x−4\),\(g(x) = \frac{2}{x}\)
Вправа\(\PageIndex{27}\)
г (х) = −5x+1, f (x) = −3х−2
- Відповідь
-
15х+11
Вправа\(\PageIndex{28}\)
\(g(x) = 3x^2 +4x−3\),\(f(x)=\frac{8}{x}\)
У вправах 29 - 36 спочатку скопіюйте заданий графік функції один до одного f (x) на свій графічний папір. Потім на тій же системі координат накидайте графік зворотної функції\(f^{−1}(x)\).
Вправа\(\PageIndex{29}\)
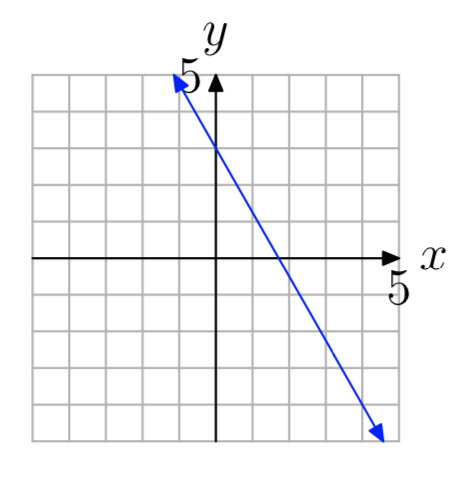
- Відповідь
-
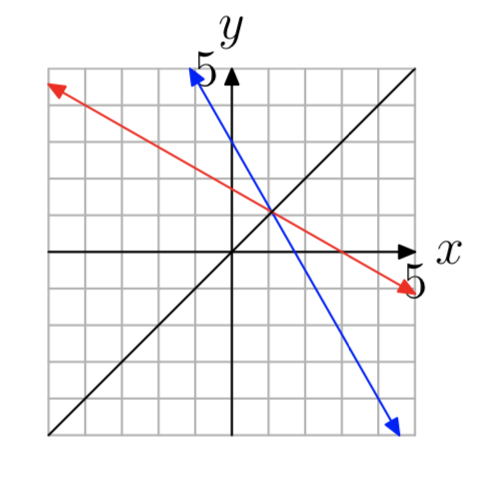
Вправа\(\PageIndex{30}\)
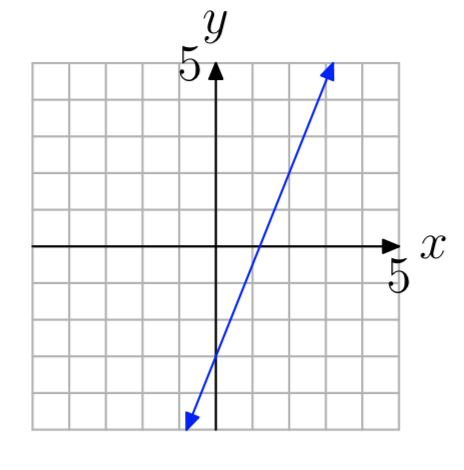
Вправа\(\PageIndex{31}\)
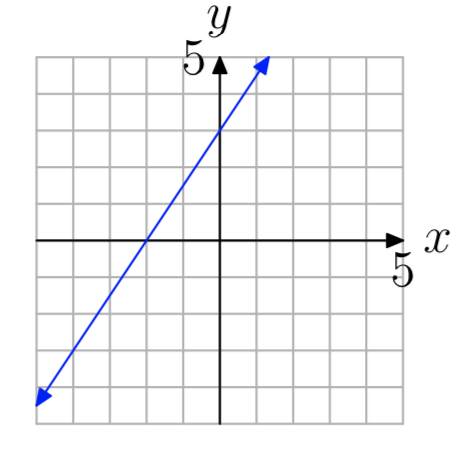
- Відповідь
-
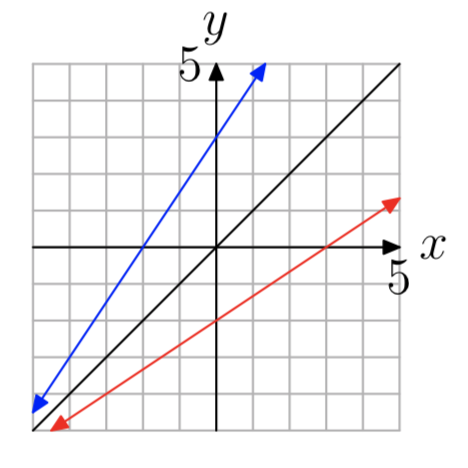
Вправа\(\PageIndex{32}\)
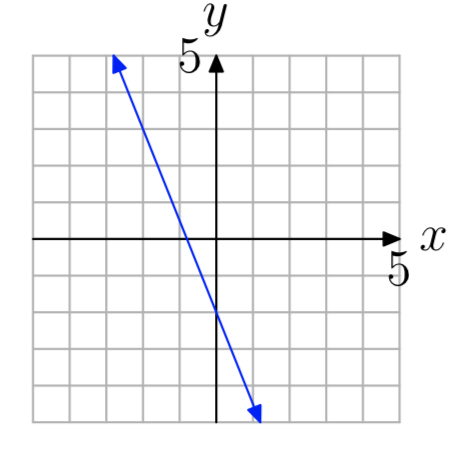
Вправа\(\PageIndex{33}\)
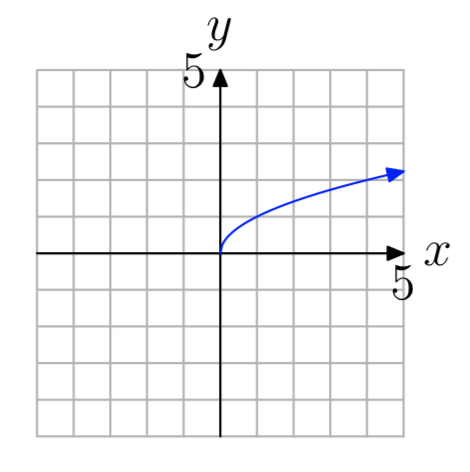
- Відповідь
-
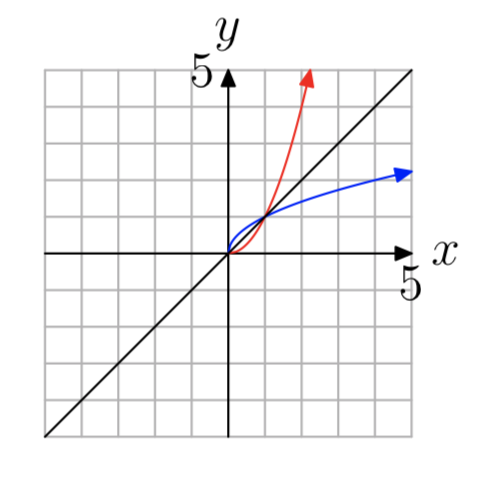
Вправа\(\PageIndex{34}\)
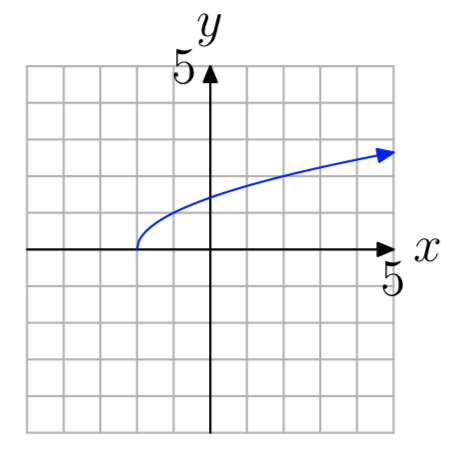
Вправа\(\PageIndex{35}\)
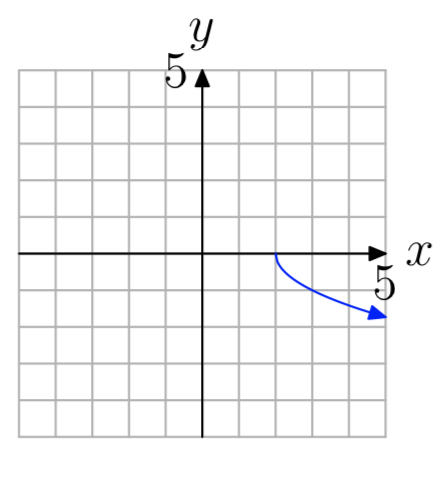
- Відповідь
-
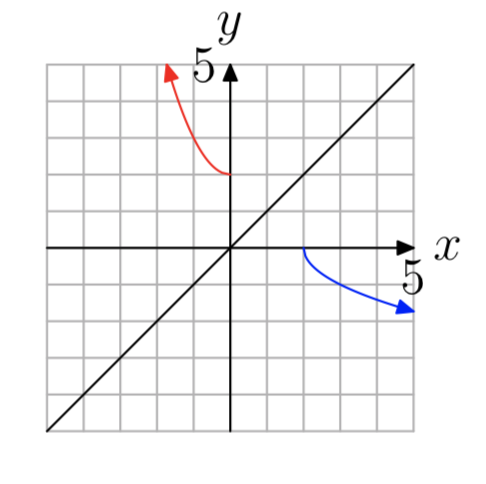
Вправа\(\PageIndex{36}\)
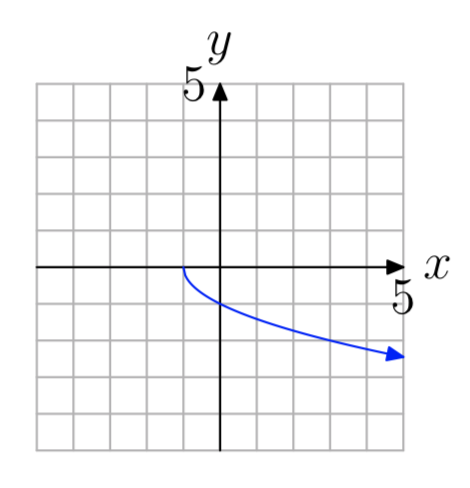
У вправах 37 - 68 знайдіть формулу для оберненої функції\(f^{−1}(x)\).
Вправа\(\PageIndex{37}\)
\(f(x) = 5x^3−5\)
- Відповідь
-
\(\sqrt[3]{\frac{x+5}{5}}\)
Вправа\(\PageIndex{38}\)
\(f(x) = 4x^7−3\)
Вправа\(\PageIndex{39}\)
\(f(x)=−\frac{9x−3}{7x+6}\)
- Відповідь
-
\(−\frac{6x−3}{7x+9}\)
Вправа\(\PageIndex{40}\)
f (х) = 6х−4
Вправа\(\PageIndex{41}\)
f (х) = 7х−9
- Відповідь
-
\(\frac{x+9}{7}\)
Вправа\(\PageIndex{42}\)
ф (х) = 7х+4
Вправа\(\PageIndex{43}\)
\(f(x) = 3x^5−9\)
- Відповідь
-
\(\sqrt[5]{\frac{x+9}{3}}\)
Вправа\(\PageIndex{44}\)
ф (х) = 6х+7
Вправа\(\PageIndex{45}\)
\(f(x) = \frac{4x+2}{4x+3}\)
- Відповідь
-
\(−\frac{3x−2}{4x−4}\)
Вправа\(\PageIndex{46}\)
\(f(x) = 5x^7+4\)
Вправа\(\PageIndex{47}\)
\(f(x) = \frac{4x−1}{2x+2}\)
- Відповідь
-
\(−\frac{2x+1}{2x−4}\)
Вправа\(\PageIndex{48}\)
\(f(x) = \sqrt[7]{8x−3}\)
Вправа\(\PageIndex{49}\)
\(f(x) = \sqrt[3]{−6x−4}\)
- Відповідь
-
\(−\frac{x^3+4}{6}\)
Вправа\(\PageIndex{50}\)
\(f(x) = \frac{8x−7}{3x−6}\)
Вправа\(\PageIndex{51}\)
\(f(x) = \sqrt[7]{−3x−5}\)
- Відповідь
-
\(−\frac{x^7+5}{3}\)
Вправа\(\PageIndex{52}\)
\(f(x) = \sqrt[9]{8x+2}\)
Вправа\(\PageIndex{53}\)
\(f(x) = \sqrt[3]{6x+7}\)
- Відповідь
-
\(\frac{x^3−7}{6}\)
Вправа\(\PageIndex{54}\)
\(f(x) = \frac{3x+7}{2x+8}\)
Вправа\(\PageIndex{55}\)
f (x) = −5x+2
- Відповідь
-
\(−\frac{x−2}{5}\)
Вправа\(\PageIndex{56}\)
ф (х) = 6х+8
Вправа\(\PageIndex{57}\)
\(f(x) = 9x^9+5\)
- Відповідь
-
\(\sqrt[9]{\frac{x−5}{9}}\)
Вправа\(\PageIndex{58}\)
\(f(x) = 4x^5−9\)
Вправа\(\PageIndex{59}\)
\(f(x) = \frac{9x−3}{9x+7}\)
- Відповідь
-
\(−\frac{7x+3}{9x−9}\)
Вправа\(\PageIndex{60}\)
\(f(x) = \sqrt[3]{9x−7}\)
Вправа\(\PageIndex{61}\)
\(f(x) = x^4\),\(x \le 0\)
- Відповідь
-
\(−\sqrt[4]{x}\)
Вправа\(\PageIndex{62}\)
\(f(x) = x^4\),\(x \ge 0\)
Вправа\(\PageIndex{63}\)
\(f(x) = x^2−1\),\(x \le 0\)
- Відповідь
-
\(−\sqrt{x+1}\)
Вправа\(\PageIndex{64}\)
\(f(x) = x^2+2\),\(x \ge 0\)
Вправа\(\PageIndex{65}\)
\(f(x) = x^4+3\),\(x \le 0\)
- Відповідь
-
\(−\sqrt[4]{x−3}\)
Вправа\(\PageIndex{66}\)
\(f(x) = x^4−5\),\(x \ge 0\)
Вправа\(\PageIndex{67}\)
\(f(x) = (x−1)^2\),\(x \le 1\)
- Відповідь
-
\(−\sqrt{x}+1\)
Вправа\(\PageIndex{68}\)
\(f(x) = (x+2)^2\),\(x \ge −2\)
