5.3: Нулі квадратичного

Ми бачили, як форма вершини та інтелектуальне використання осі симетрії можуть допомогти намалювати точний графік квадратичної функції, визначеної рівнянням$f(x) = ax^2+bx+c$. При малюванні графіка параболи корисно знати, де графік параболи перетинає вісь x. Тобто основна мета цього розділу, знайти нульові переходи або х-перехоплення параболи.

Перш ніж ми почнемо, вам потрібно буде переглянути методи, які дозволять вам зарахувати квадратичний вираз$ax^2 + bx + c$.

Факторинг$ax^2 + bx + c$ при a = 1

Наша мета в цьому розділі полягає в тому, щоб забезпечити швидкий огляд методів, що використовуються для фактора квадратичних триноміалів. Почнемо з показу, як множити триноми$ax^2 + bx + c$, що мають вигляд, де провідним коефіцієнтом є a = 1; тобто триноми, що мають форму$x^2+bx+c$. У наступному розділі ми розглянемо техніку, яка використовується для врахування,$ax^2+bx+c$ коли$a \neq 1$.

Почнемо з прикладу.

Приклад$\PageIndex{1}$

Фактор$x^{2}+16 x-36$

Рішення

Зверніть увагу, що провідний коефіцієнт$x^2$, коефіцієнт, дорівнює 1. Це важливе спостереження, адже методика, представлена тут, не спрацює, коли провідний коефіцієнт не дорівнює 1.

Зауважте, що постійний термін триноміалу$x^2 + 16x − 36$ дорівнює −36. Перелічити всі цілі пари, добуток яких дорівнює −36.

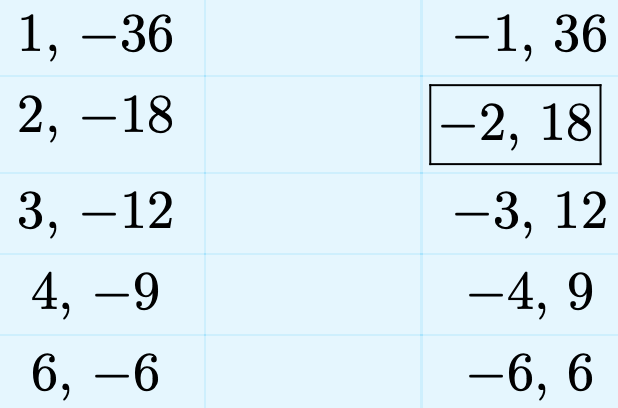
Зауважте, що ми обрамляли пару −2, 18. Ми зробили це тому, що сума цієї пари цілих чисел дорівнює коефіцієнту х в триноміальному виразі$x^2 + 16x − 36$. Використовуйте цю рамку пари для фактора тріноміалу.

$$x^{2}+16 x-36=(x-2)(x+18)$$

Важливо, щоб ви перевіряли свій результат. Використовуйте розподільну властивість для множення.

$$\begin{aligned}(x-2)(x+18) &=x(x+18)-2(x+18) \\ &=x^{2}+18 x-2 x-36 \\ &=x^{2}+16 x-36 \end{aligned}$$

Таким чином, наша факторизація правильна.

Підіб'ємо підсумки методики.

Алгоритм

Для фактора квадратичного$x^2 + bx + c$, дійте наступним чином:

1. Перерахуйте всі цілі пари, добуток яких дорівнює c.
2. Обведіть або обрамте пару, сума якої дорівнює коефіцієнту x, а саме b. Скористайтеся цією парою для множення триноміалу.

Давайте розглянемо інший приклад.

Приклад$\PageIndex{2}$

Фактор триноміалу$x^{2}-25 x-84$

Рішення

Перерахуйте всі цілі пари, добуток яких дорівнює −84.

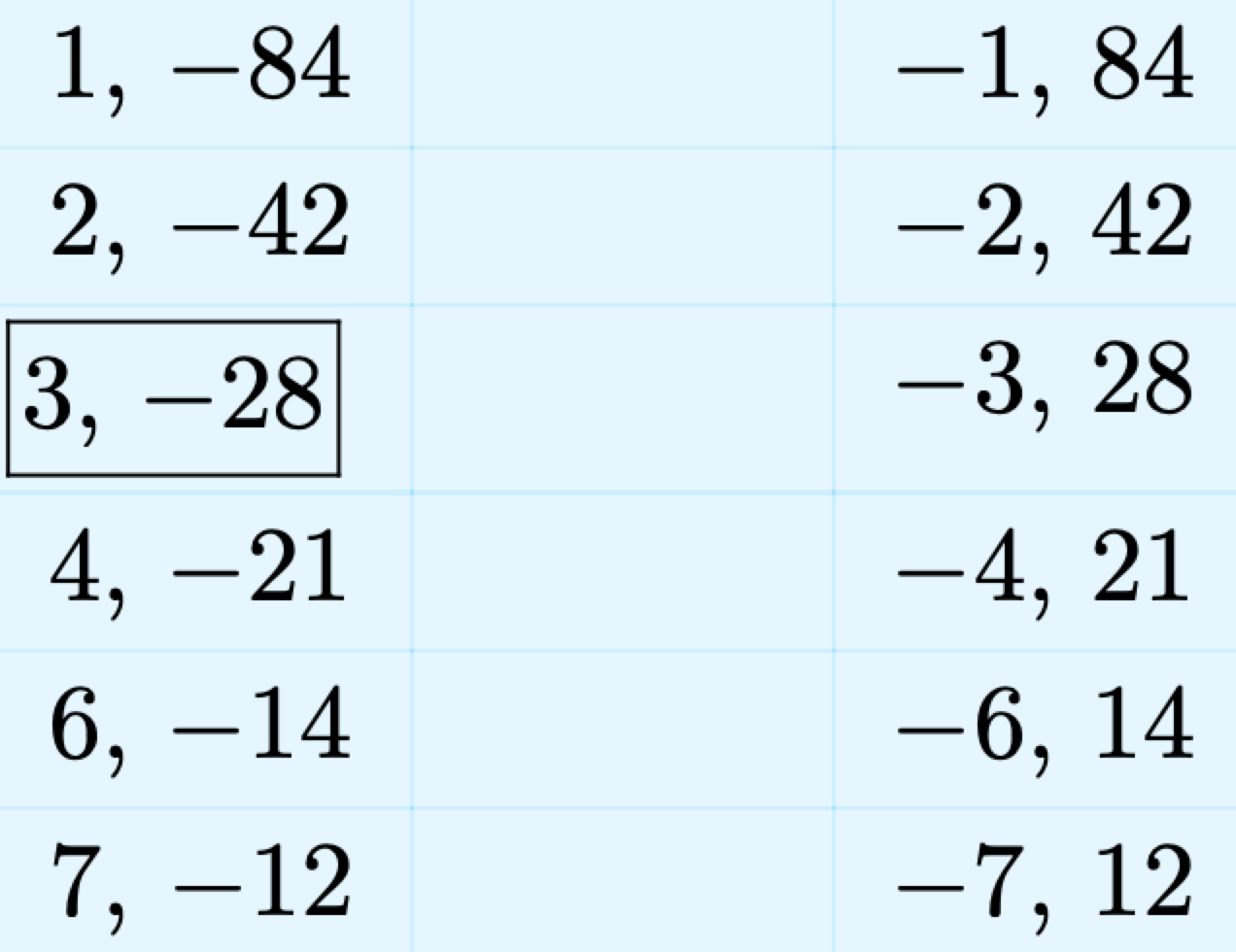
Ми обрамляли пару, сума якої дорівнює коефіцієнту x, а саме −25. Використовуйте цю пару для фактора триноміалу.

$$x^{2}-25 x-84=(x+3)(x-28) \nonumber$$

Перевірити

$$\begin{aligned}(x+3)(x-28) &=x(x-28)+3(x-28) \\ &=x^{2}-28 x+3 x-84 \\ &=x^{2}-25 x-84 \end{aligned}$$

Маючи досвід, є ряд ідей, які прискорюють процес.

• Коли ви перераховуєте цілочисельні пари, якщо ви зауважите, що поточна пара має відповідну суму, немає необхідності перераховувати решту цілих пар. Просто зупиніть процес перерахування цілих пар і використовуйте поточну пару для множника триноміала.
• Деякі студенти цілком щасливі, коли їх запитують: «Чи можете ви придумати цілу пару, добуток якої дорівнює c, а сума якої дорівнює b (де b і c посилаються на коефіцієнти$x^2 +bx+c$)?» Якщо ви можете підібрати пару «з повітря» так, все добре і добре.

Використовуйте цілу пару для множника триноміалу і не турбуйтеся про перерахування будь-яких цілих пар.

Тепер давайте розберемо, як діяти, коли провідний коефіцієнт не дорівнює 1.

Факторинг$a x^{2}+b x+c$ при$a \neq 1$

Коли$a \neq 1$, ми використовуємо техніку під назвою ac-test для фактора триноміала$ax^2 + bx + c$. Процес найкраще пояснити на прикладі.

Приклад$\PageIndex{3}$

Фактор$2x^2 + 13x − 24$.

Рішення

Зверніть увагу, що провідний коефіцієнт не дорівнює 1. Дійсно, коефіцієнт$x^2$ в даному прикладі дорівнює 2. Тому техніка попередніх прикладів не підійде. Таким чином, перейдемо до подібної методики під назвою ac-test.

По-перше, порівняйте $$2 x^{2}+13 x-24 \qquad \text { and } \qquad a x^{2}+b x+c$$

і зверніть увагу, що a = 2, b = 13, а c = −24. Обчислити добуток a і c Ось так техніка заробляє свою назву «ac-test».

$$a c=(2)(-24)=-48 \nonumber$$

Перерахуйте всі цілі пари, добуток яких дорівнює ac = −48.

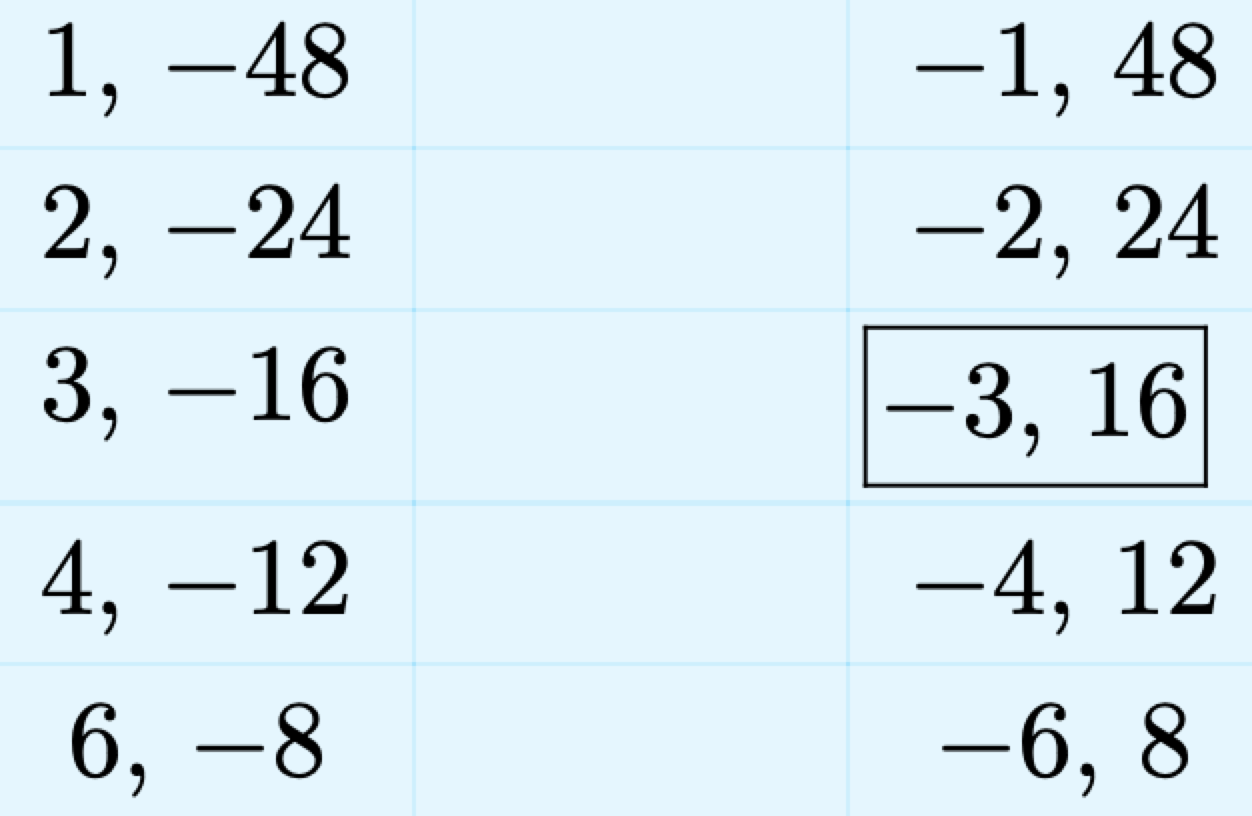
Ми обрамляли пару, сума якої b = 13. Наступний крок - переписати триноміал$2x^2 + 13x − 24$, розділивши середній член на суму, використовуючи нашу обрамлену цілу пару.

$$2 x^{2}+13 x-24=2 x^{2}-3 x+16 x-24 \nonumber$$

Ми множимо х з перших двох членів, а потім 8 з останніх двох термінів. Цей процес називається факторингом шляхом групування.

$$2 x^{2}-3 x+16 x-24=x(2 x-3)+8(2 x-3) \nonumber$$

Тепер ми враховуємо загальний коефіцієнт 2x − 3.

$$x(2 x-3)+8(2 x-3)=(x+8)(2 x-3) \nonumber$$

Корисно бачити повний процес як цілісну одиницю.

$$\begin{aligned} 2 x^{2}+13 x-24 &=2 x^{2}-3 x+16 x-24 \\ &=x(2 x-3)+8(2 x-3) \\ &=(x+8)(2 x-3) \end{aligned}$$

Перевірити

Знову ж таки, важливо перевірити відповідь множенням.

$$\begin{aligned}(x+8)(2 x-3) &=x(2 x-3)+8(2 x-3) \\ &=2 x^{2}-3 x+16 x-24 \\ &=2 x^{2}+13 x-24 \end{aligned}$$

Оскільки це оригінальний триноміал, наше рішення перевіряє.

Підіб'ємо підсумок цього процесу.

Алгоритм: AC-тест

Для фактора квадратичного$ax^2 + bx + c$, дійте наступним чином:

1. Перерахуйте всі цілі пари, твір яких дорівнює ac.
2. Обведіть або обрамляйте пару, сума якої дорівнює коефіцієнту x, а саме b.
3. Використовуйте обведену колом пару, щоб висловити середній член bx як суму.
4. Фактор за «групуванням».

Давайте розглянемо інший приклад.

Приклад$\PageIndex{4}$

Фактор$3 x^{2}+34 x-24$

Рішення

Порівняти

$$3 x^{2}+34 x-24 \quad \text { and } \quad a x^{2}+b x+c \nonumber$$

і зверніть увагу, що a = 3, b = 34 і c = −24. Перелічити всі цілі пари, добуток яких дорівнює ac = (3) (−24) = −72.

Ми обрамляли пару, сума якої така ж, як b = 34, коефіцієнт х в$3x^2 + 34x − 24$. Знову ж таки, можливі ярлики. Якщо ви можете «думати» про пару, добуток якої дорівнює ac = −72 і сума якої дорівнює b = 34, то не потрібно перераховувати будь-які цілочисельні пари. Крім того, якщо ви зіткнетеся з потрібною парою, коли ви їх перераховуєте, то ви можете зупинити процес. Немає необхідності перераховувати інші пари, якщо у вас є та, яка вам потрібна.

Використовуйте обрамлену пару, щоб висловити середній член як суму, а потім коефіцієнт шляхом групування.

$$\begin{aligned} 3 x^{2}+34 x-24 &=3 x^{2}-2 x+36 x-24 \\ &=x(3 x-2)+12(3 x-2) \\ &=(x+12)(3 x-2) \end{aligned}$$

Ми залишаємо це читачеві, щоб перевірити цей результат.

Перехоплює

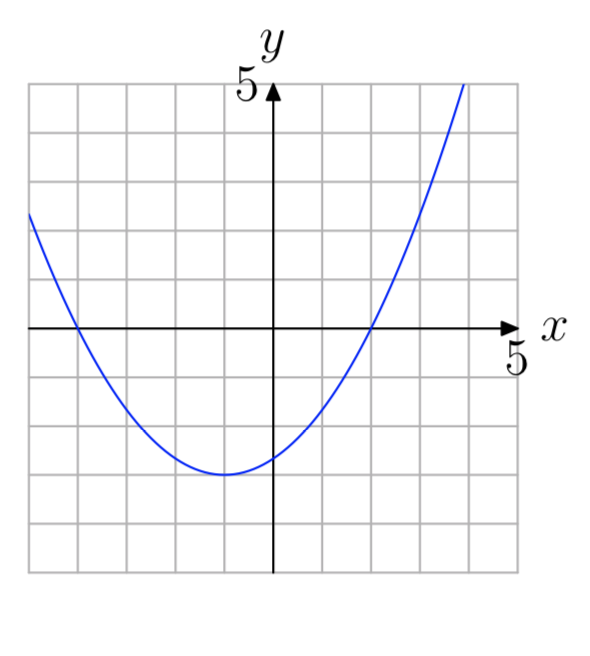
Точки, де графік функції перетинає вісь x, називаються x-перехопленнями графіка функції. Розглянемо графік квадратичної функції f на рис$\PageIndex{1}$.

Малюнок$\PageIndex{1}$: X- і y-перехоплення є ключовими ознаками будь-якого графіка.

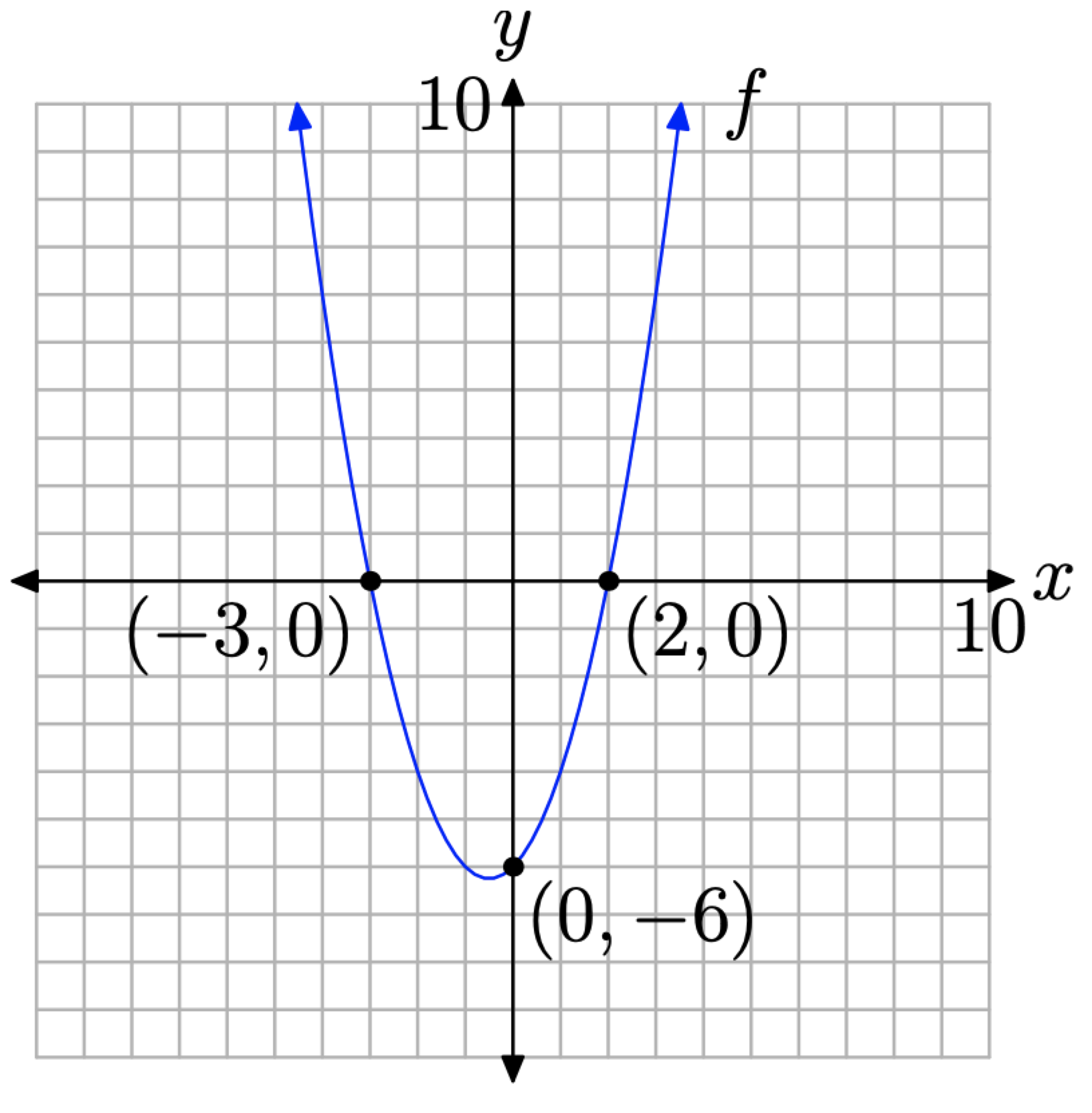
Зауважте, що графік f перетинає вісь x в (−3, 0) та (2, 0). Це X-перехоплення параболи. Зверніть увагу, що y-координата кожного перехоплення x дорівнює нулю.

У позначеннях функцій розв'язки f (x) = 0 (зверніть увагу на схожість з y = 0) є x-координатами точок, де графік f перетинає вісь x. Аналізуючи графік f на малюнку$\PageIndex{1}$, ми бачимо, що і −3, і 2 є розв'язками f (x) = 0.

Таким чином, процес знаходження х-перехоплень зрозумілий.

Пошук х-перехоплень

Щоб знайти x-перехоплення графа будь-якої функції, встановіть y = 0 і вирішіть для x. Або ж, якщо використовується позначення функції, встановіть f (x) = 0 і вирішіть для x.

Давайте розглянемо приклад.

Приклад$\PageIndex{5}$

Знайти x-перехоплення графа квадратичної функції, визначеної$y = x^2 + 2x − 48$.

Рішення

Щоб знайти x-перехоплення, спочатку встановіть y = 0.

$$0=x^{2}+2 x-48$$

Далі вважте тріноміал праворуч. Зверніть увагу, що коефіцієнт$x^2$ дорівнює 1. Нам потрібно думати лише про два цілих числа, добуток яких дорівнює постійному терміну −48, а сума яких дорівнює коефіцієнту x, а саме 2. Числа 8 і −6 приходять на розум, тому триноміальні фактори виглядають наступним чином (читачі повинні перевірити цей результат).

$$0=(x+8)(x-6)$$

Для завершення рішення нам потрібно використовувати важливу властивість дійсних чисел, яке називається властивістю нульового добутку.

Нульова властивість продукту

Якщо a і b - будь-які дійсні числа такі $$ab = 0$$ , що, то або a = 0, або b = 0.

У нашому випадку ми маємо 0 = (x + 8) (x − 6). Тому повинно бути так, що або

$$x+8=0 \qquad \text { or } \qquad x-6=0$$

Ці рівняння можуть бути вирішені самостійно для отримання

$$x=-8 \quad \text { or } \quad x=6$$

Таким чином, x-перехоплення графа$y = x^2 + 2x−48$ розташовані за адресами (−8, 0) та (6, 0).

Давайте розглянемо інший приклад.

Приклад$\PageIndex{6}$

Знайти x-перехоплення графа квадратичної функції$f(x) = 2x^2 − 7x − 15$.

Рішення

Щоб знайти x-перехоплення графа квадратичної функції f, починаємо з установки

$$f(x)=0\nonumber$$

Звичайно$f(x) = 2x^2 − 7x − 15$, тому ми можемо замінити, щоб отримати

$$2 x^{2}-7 x-15=0 \nonumber$$

Тепер ми будемо використовувати ac-тест для фактора тріноміала зліва. Зауважте, що ac = (2) (−15) = −30. Перерахуйте цілочисельні пари, добуток яких дорівнює −30.

Зверніть увагу, що обрамлена пара дорівнює коефіцієнту x in$2x^2 − 7x − 15$. Використовуйте обрамлену пару, щоб висловити середній член як суму, а потім коефіцієнт шляхом групування

$$\begin{aligned} 2 x^{2}-7 x-15 &=0 \\ 2 x^{2}+3 x-10 x-15 &=0 \\ x(2 x+3)-5(2 x+3) &=0 \\(x-5)(2 x+3) &=0 \end{aligned}$$

Тепер ми можемо використовувати властивість нульового продукту. Або

$$x-5=0 \qquad \text { or } \qquad 2 x+3=0 \nonumber$$

Кожне з них можна вирішити самостійно, щоб отримати

$$x=5 \qquad \text { or } \qquad x=-3 / 2 \nonumber$$

Таким чином, x-перехоплення графа квадратичної функції$f(x) = 2x^2 − 7x − 15$ розташовані за адресами (−3/2, 0) та (5, 0).

Ще одне визначення по порядку.

Визначення 7: Нулі функції

Розв'язки f (x) = 0 називаються нулями функції f.

Таким чином, в останньому прикладі обидва −3/2 і 5 є нулями квадратичної функції$f(x) = 2x^2−7x−15$. Зверніть увагу на інтимний зв'язок між нулями квадратичної функції і x-перехопленнями графіка. Зауважте, що −3/2 є нулем і (−3/2, 0) є перехопленням x. Аналогічно 5 - це нуль і (5, 0) - перехоплення х.

Калькулятор графіків може бути використаний для пошуку нулів функції.

Приклад$\PageIndex{7}$

Використовуйте графічний калькулятор, щоб знайти нулі функції$f(x) = 2x^2 − 7x − 15$.

Рішення

Введіть функцію$f(x) = 2x^2 − 7x − 15\_ into Y1 in the Y= menu; then adjust the window parameters as shown in Figure \(\PageIndex{2}$ (b). Натисніть кнопку GRAPH, щоб створити параболу, показану на малюнку$\PageIndex{2}$ (c).

Щоб знайти нуль функції, дійте наступним чином:

Малюнок$\PageIndex{2}$. Побудова квадратичної функції$f(x) = 2x^2 − 7x − 15$.

• Натисніть 2nd TRACE, щоб відкрити вікно РОЗРАХУВАТИ, показане на малюнку$\PageIndex{3}$ (а). У цьому меню виберіть 2:нуль.
• Калькулятор відповідає, запитуючи «Ліва межа». За допомогою клавіш зі стрілками перемістіть курсор трохи лівіше крайнього лівого перехоплення x, як показано на малюнку$\PageIndex{3}$ (b). Натисніть клавішу ENTER.
• Калькулятор відповідає, запитуючи «Праворуч прив'язаний». За допомогою клавіш зі стрілками перемістіть курсор трохи праворуч від крайнього лівого перехоплення x, як показано на малюнку$\PageIndex{3}$ (c). Натисніть клавішу ENTER.
• Калькулятор відповідає, запитуючи «Вгадай». Ви можете використовувати клавіші зі стрілками, щоб вибрати початкове значення x у будь-якому місці між вибраними лівою та правою межею (зауважте, що калькулятор позначає їх на екрані на малюнку$\PageIndex{3}$ (d)). Однак курсор вже лежить між цими позначками, тому ми зазвичай просто натискаємо ENTER в цей момент. Ми пропонуємо вам зробити це також.

Малюнок$\PageIndex{3}$. За допомогою нульової утиліти знайти x-перехоплення.

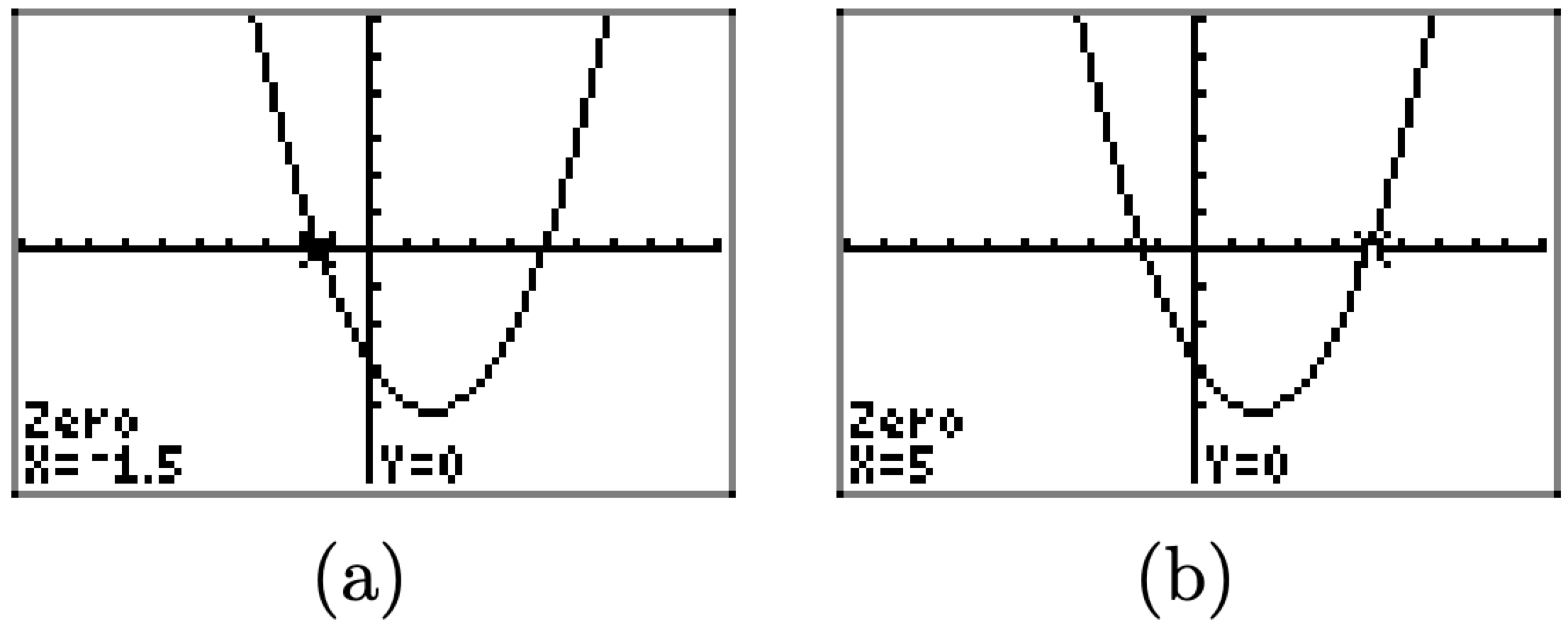
Калькулятор реагує позначенням x-перехоплення та повідомленням про його значення x внизу екрана, як показано на малюнку$\PageIndex{4}$ (а). Це один з нулів функції. Зауважте, що це значення −1.5 добре узгоджується з нашим розрахунковим результатом −3/2 у прикладі$\PageIndex{6}$. Ми дотримувалися точно тієї ж процедури, описаної вище, щоб знайти другий x-перехоплення, показаний на малюнку$\PageIndex{4}$ (b). Зверніть увагу, що він також узгоджується з розрахунком руки рішення Приклад$\PageIndex{6}$.

У подібному ключі точка, де графік функції перетинає вісь y, називається y-перехопленням графіка функції. На$\PageIndex{1}$ малюнку y-перехоплення параболи дорівнює (0, −6). Зверніть увагу, що координата x цього y-перехоплення дорівнює нулю.

Таким чином, процес знаходження y-перехоплень повинен бути зрозумілим.

Малюнок$\PageIndex{4}$: Нулі$f(x) − 2x^2 − 7x − 15$.

Пошук Y-перехоплень

Щоб знайти y-перехоплення графіка будь-якої функції, задаємо$x = 0$ і вирішуємо для$y$. Крім того, якщо використовується позначення функції, просто оцініть f (0).

Приклад$\PageIndex{8}$

Знайти y-перехоплення квадратичної функції, визначеної$f(x) = x^2 − 3x − 11$.

Рішення

Оцініть функцію при x = 0.

$$f(0)=(0)^{2}-3(0)-11=-11$$

Координати перехоплення y мають значення (0, −11).

Збираємо все разом

Ми знайдемо як x-, так і y-перехоплення надзвичайно корисними при малюванні графіка квадратичної функції.

Приклад$\PageIndex{9}$

Помістіть квадратичну функцію$y = x^2 + 2x − 24$ у вигляді вершини. Побудуйте вершину і вісь симетрії та позначте їх координатами та рівнянням відповідно. Знайдіть і побудуйте x- і y-перехоплення параболи і позначте їх координатами.

Рішення

Візьміть половину коефіцієнта х, квадрат, потім складіть і відніміть цю суму, щоб збалансувати рівняння. Коефіцієнти множника і комбінувати.

$$\begin{array}{l}{y=x^{2}+2 x+1-1-24} \\ {y=(x+1)^{2}-25}\end{array}$$

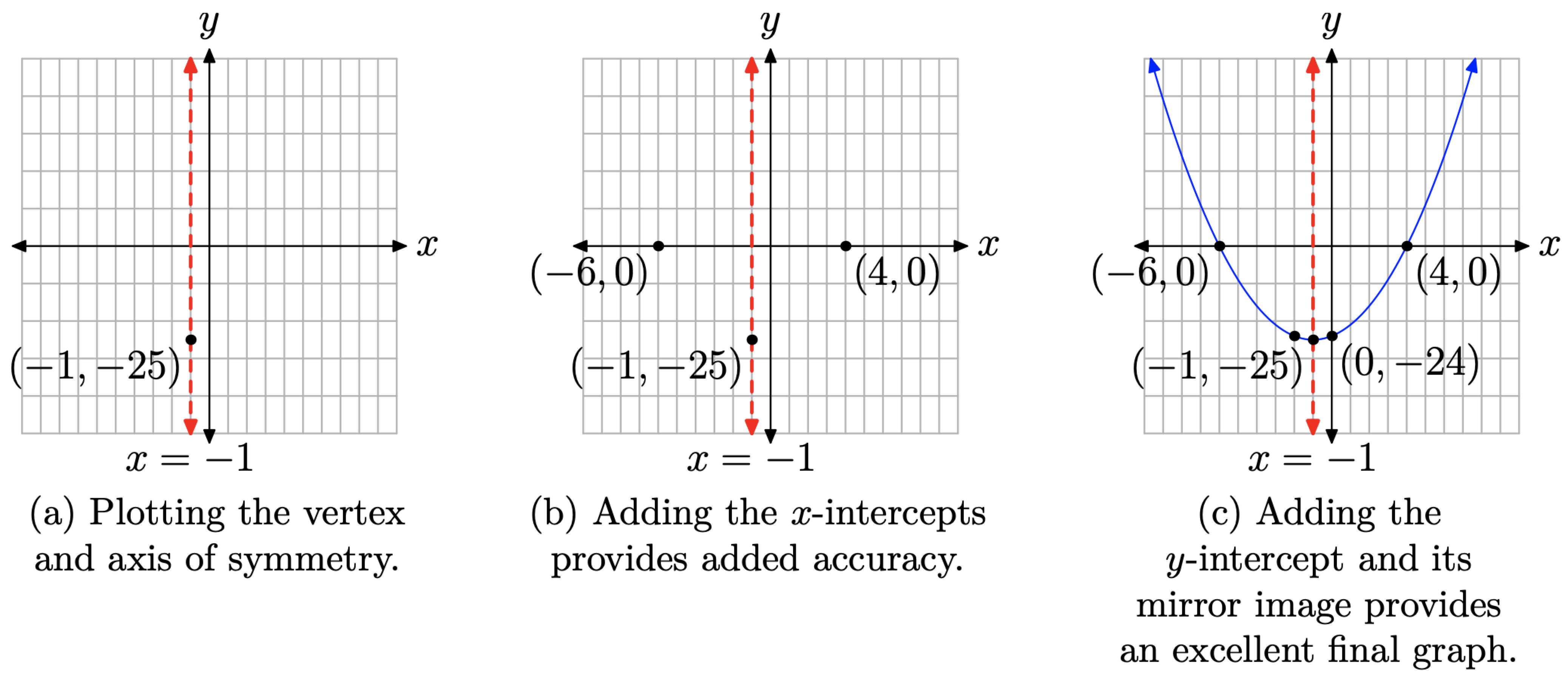
Графік являє собою параболу, яка відкривається вгору; вона зрушена на 1 одиницю вліво і на 25 одиниць вниз. Цієї інформації достатньо для побудови та позначення вершини, а потім побудови та маркування осі симетрії, як показано на малюнку$\PageIndex{5}$ (а).

Щоб знайти x-перехоплення, нехай y = 0 in$y = x^2 + 2x − 24$.

$$0=x^{2}+2 x-24 \nonumber$$

Провідний коефіцієнт дорівнює 1. Пара цілих чисел −4 та 6 має добуток −24 та суму 2. Таким чином, права сторона чинників наступним чином.

$$0=(x+6)(x-4) \nonumber$$

Для того, щоб цей продукт дорівнював нулю, або

$$x+6=0 \qquad \text { or } \qquad x-4=0 \nonumber$$

Вирішіть кожне з цих лінійних рівнянь незалежно.

$$x=-6 \qquad \text { or } \qquad x=4 \nonumber$$

Нагадаємо, що ми дозволяємо y = 0. Ми знайшли два розв'язки: x = −6 і x = 4. Таким чином, ми маємо x-перехоплення на (−6, 0) та (4, 0), як показано на малюнку$\PageIndex{5}$ (b).

Нарешті, щоб знайти y-перехоплення, нехай x = 0 in$y = x^2+2x−24$. При цій підстановці y = −24. Таким чином, y-перехоплення дорівнює (0, −24), як показано на малюнку$\PageIndex{5}$ (c). Зауважте, що ми також включили дзеркальне зображення перехоплення y-перехоплення по осі симетрії.

Малюнок$\PageIndex{5}$

Давайте розглянемо один остаточний приклад.

Приклад$\PageIndex{10}$

Побудуйте параболу, представлену рівнянням$f(x) = −2x^2−7x+15$. Побудуйте та позначте вершину, вісь симетрії та x- та y-перехоплення.

Рішення

По-перше, виведіть значення −2.

$$f(x)=-2\left[x^{2}+\frac{7}{2} x-\frac{15}{2}\right] \nonumber$$

Половина 7/2 становить 7/4. У квадраті це становить 49/16. Додайте і відніміть цю останню суму, щоб рівняння було збалансованим.

$$f(x)=-2\left[x^{2}+\frac{7}{2} x+\frac{49}{16}-\frac{49}{16}-\frac{15}{2}\right]$$

Перші три члени всередині дужок утворюють ідеальний квадратний триноміал. Останні дві константи об'єднані загальним знаменником.

$$\begin{array}{l}{f(x)=-2\left[\left(x^{2}+\frac{7}{2} x+\frac{49}{16}\right)-\frac{49}{16}-\frac{120}{16}\right]} \\ {f(x)=-2\left[\left(x+\frac{7}{4}\right)^{2}-\frac{169}{16}\right]}\end{array}$$

Нарешті, перерозподіліть −2.

$$f(x)=-2\left(x+\frac{7}{4}\right)^{2}+\frac{169}{8}$$

Графік цього останнього рівняння являє собою параболу, яка відкривається вниз, перекладена 7/4 одиниць вліво і 169/8 одиниць вгору. Цієї інформації достатньо для побудови та позначення вершини та осі симетрії, як показано на малюнку$\PageIndex{6}$ (а).

Щоб знайти y-перехоплення, встановіть f (x) = 0 in$f(x) = −2x^2 − 7x + 15$. Ми також помножимо обидві сторони отриманого рівняння на −1.

$$\begin{array}{l}{0=-2 x^{2}-7 x+15} \\ {0=2 x^{2}+7 x-15}\end{array}$$

Після порівняння$2x^2 + 7x − 15$ з$ax^2 + bx + c$, відзначимо, що цілі пари −3 і 10 мають добуток, рівний ac = −30 і суму, рівну b = 7. Використовуйте цю пару, щоб висловити середній член$2x^2 + 7x − 15$ як суму, а потім множник шляхом групування.

$$\begin{array}{l}{0=2 x^{2}-3 x+10 x-15} \\ {0=x(2 x-3)+5(2 x-3)} \\ {0=(x+5)(2 x-3)}\end{array}$$

За властивістю нульового продукту, або $$x+5=0 \qquad \text { or } \qquad 2 x-3=0$$

Вирішити ці лінійні рівняння самостійно. $$x=-5 \qquad \text { or } \qquad x=\frac{3}{2}$$

Ці значення x є нулями f (вони роблять f (x) = 0), тому ми маємо x-перехоплення в (−5, 0) і (3/2, 0), як показано на малюнку$\PageIndex{6}$ (b).

Малюнок$\PageIndex{6}$

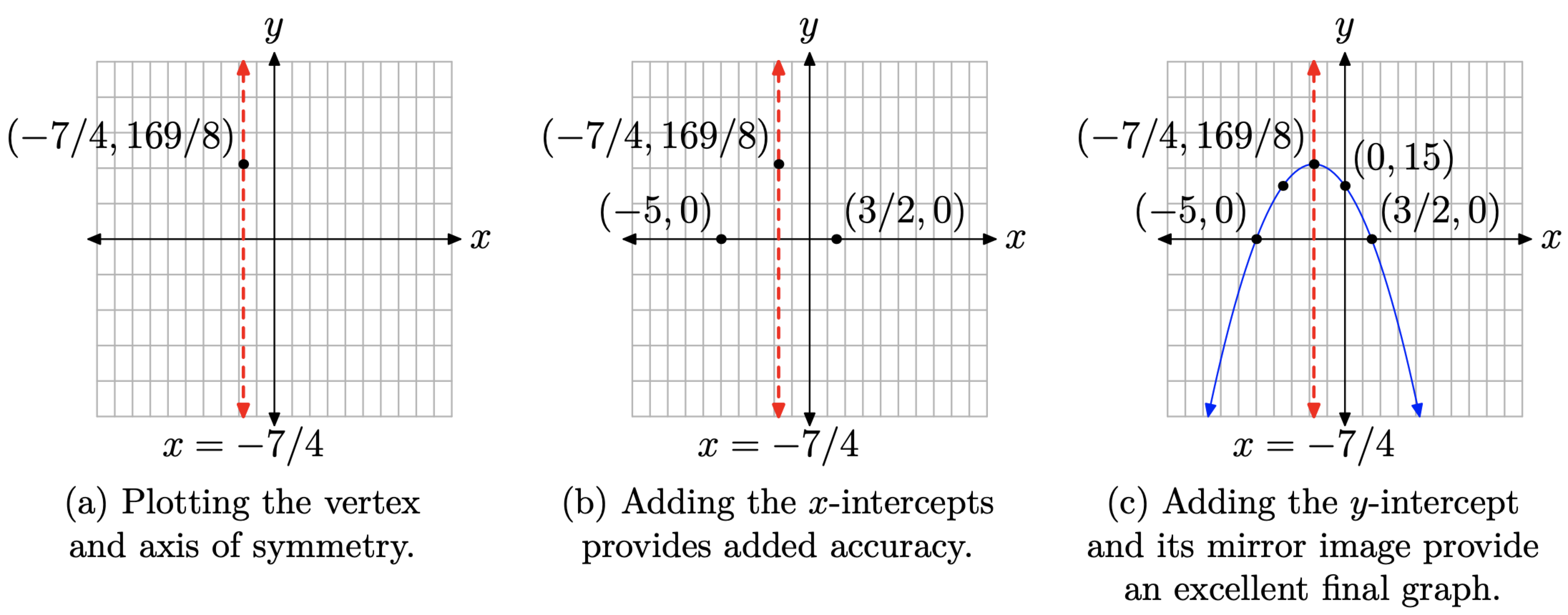
Нарешті, щоб знайти y-перехоплення, встановіть x = 0 in,$f(x) = −2x^2 − 7x + 15$ щоб отримати f (0) = 15. Зверніть увагу на позиціонування y-перехоплення (0, 15) та його дзеркальне відображення поперек осі симетрії на малюнку$\PageIndex{6}$ (c).

Вправа

У вправах 1 - 8 множник заданого квадратичного многочлена.

Вправа$\PageIndex{1}$

$x^2+9x+14$

Відповідь

(х+2) (х+7)

Вправа$\PageIndex{2}$

$x^2+6x+5$

Вправа$\PageIndex{3}$

$x^2+10x+9$

Відповідь

(х+9) (х+1)

Вправа$\PageIndex{4}$

$x^2+4x−21$

Вправа$\PageIndex{5}$

$x^2−4x−5$

Відповідь

(х−5) (х+1)

Вправа$\PageIndex{6}$

$x^2+7x−8$

Вправа$\PageIndex{7}$

$x^2−7x+12$

Відповідь

(x−4) (x−3)

Вправа$\PageIndex{8}$

$x^2+5x−24$

У вправах 9 - 16 знайдіть нулі заданої квадратичної функції.

Вправа$\PageIndex{9}$

$f(x) = x^2−2x−15$

Відповідь

Нулі: x = −3, x = 5

Вправа$\PageIndex{10}$

$f(x) = x^2+4x−32$

Вправа$\PageIndex{11}$

$f(x) = x^2+10x−39$

Відповідь

Нулі: x = −13, x = 3

Вправа$\PageIndex{12}$

$f(x) = x^2+4x−45$

Вправа$\PageIndex{13}$

$f(x) = x^2−14x+40$

Відповідь

Нулі: х = 4, х = 10

Вправа$\PageIndex{14}$

$f(x) = x^2−5x−14$

Вправа$\PageIndex{15}$

$f(x) = x^2+9x−36$

Відповідь

Нулі: x = −12, x = 3

Вправа$\PageIndex{16}$

$f(x) = x^2+11x−26$

У Вправах 17 - 22 виконайте кожне з наступних завдань для квадратичних функцій.

1. Завантажте функцію в Y1 Y= вашого графічного калькулятора. Налаштуйте параметри вікна так, щоб вершина була видна у вікні перегляду.
2. Налаштуйте систему координат на домашньому папері. Позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax. Зробіть розумну копію зображення у вікні перегляду вашого калькулятора на цій системі координат і позначте її рівнянням.
3. Використовуйте нульову утиліту на графічному калькуляторі, щоб знайти нулі функції. Використовуйте ці результати для побудови x-перехоплень у вашій системі координат та позначення їх координатами.
4. Використовуйте суворо алгебраїчну техніку (без калькулятора), щоб знайти нулі заданої квадратичної функції. Покажіть свою роботу поруч із вашою системою координат. Будьте вперті! Працюйте над проблемою, поки ваші алгебраїчні та графічно нулі не будуть розумним збігом.

Вправа$\PageIndex{17}$

$f(x) = x^2+5x−14$

Відповідь

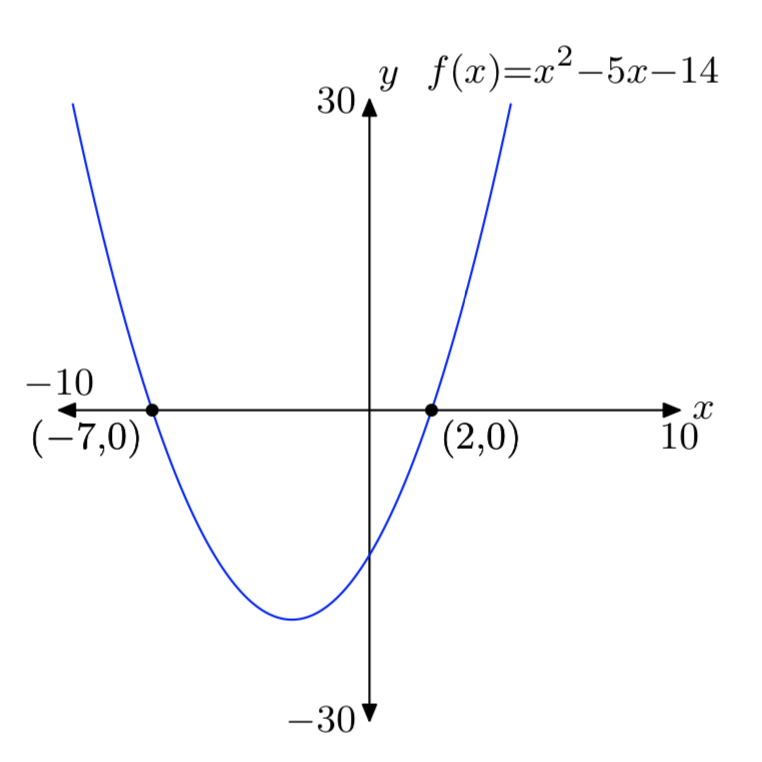
Вправа$\PageIndex{18}$

$f(x) = x^2+x−20$

Вправа$\PageIndex{19}$

$f(x) = −x^2+3x+18$

Відповідь

Вправа$\PageIndex{20}$

$f(x) = −x^2+3x+40$

Вправа$\PageIndex{21}$

$f(x) = x^2−16x−36$

Відповідь

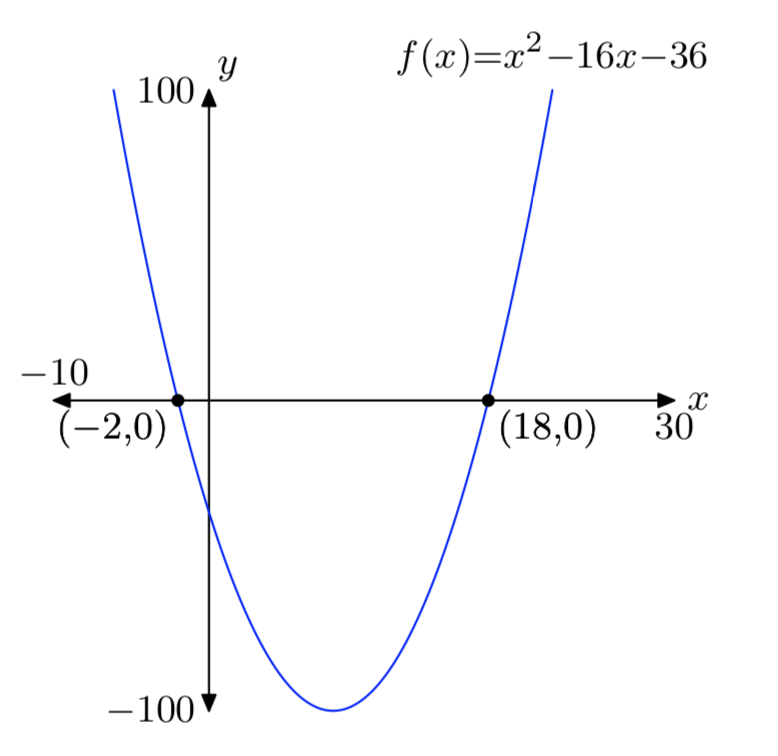
Вправа$\PageIndex{22}$

$f(x) = x^2+4x−96$

У Вправах 23 - 30 виконайте кожне з наступних завдань для заданої квадратичної функції.

1. Налаштуйте систему координат на графічному папері. Позначте та масштабуйте кожну вісь. Не забудьте намалювати всі лінії лінійкою.
2. Використовуйте техніку завершення квадрата, щоб розмістити квадратичну функцію у вигляді вершини. Покладіть вершину на вашій системі координат і позначте її координатами. Намалюйте вісь симетрії на вашій системі координат і позначте її рівнянням.
3. Використовуйте суворо алгебраїчну техніку (без калькуляторів), щоб знайти х-перехоплення графа заданої квадратичної функції. Покладіть їх на вашій системі координат і позначте їх координатами.
4. Знайти y-перехоплення графа квадратичної функції. Покладіть y-перехоплення на вашій системі координат та його дзеркальне відображення поперек осі симетрії, а потім позначте ці точки їх координатами.
5. Використовуючи всю побудовану інформацію, намалюйте графік квадратичної функції і позначте його вершинної формою її рівняння. Використовуйте інтервальне позначення для опису області та діапазону квадратичної функції.

Вправа$\PageIndex{23}$

$f(x) = x^2+2x−8$

Відповідь

Домен = ($−\infty, \infty$), Діапазон = [−9,$\infty$)

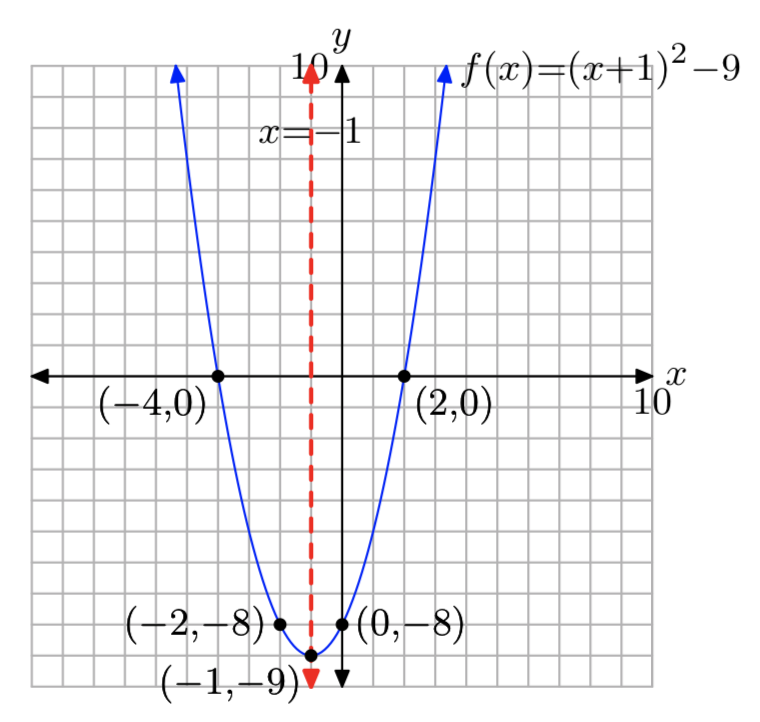
Вправа$\PageIndex{24}$

$f(x) = x^2−6x+8$

Вправа$\PageIndex{25}$

$f(x) = x^2+4x−12$

Відповідь

Домен = ($−\infty, \infty$), Діапазон = [−16,$\infty$)

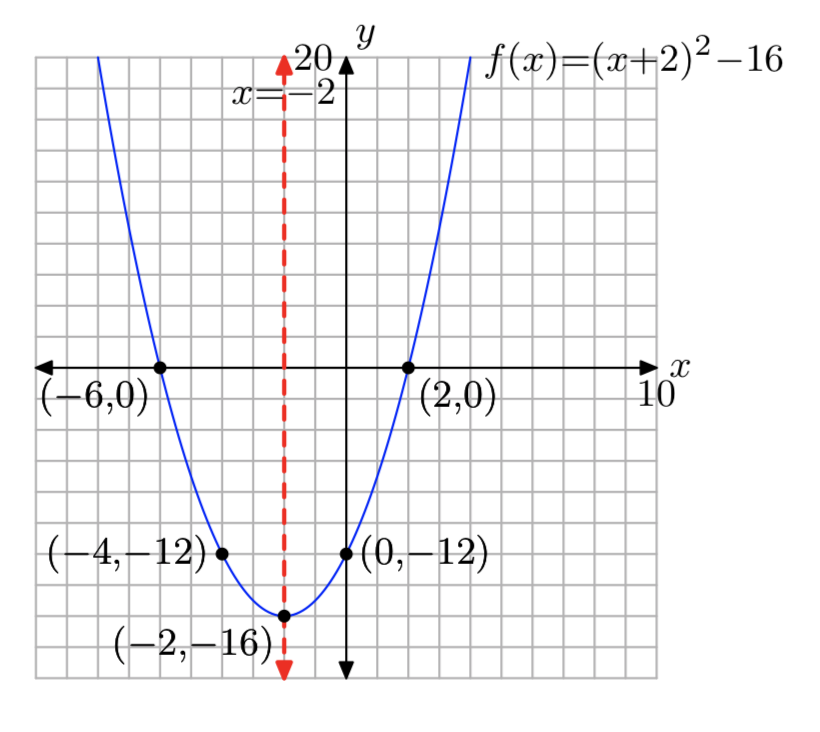
Вправа$\PageIndex{26}$

$f(x) = x^2+8x+12$

Вправа$\PageIndex{27}$

$f(x) = −x^2−2x+8$

Відповідь

Домен = ($−\infty, \infty$), Діапазон = ($−\infty$, 9]

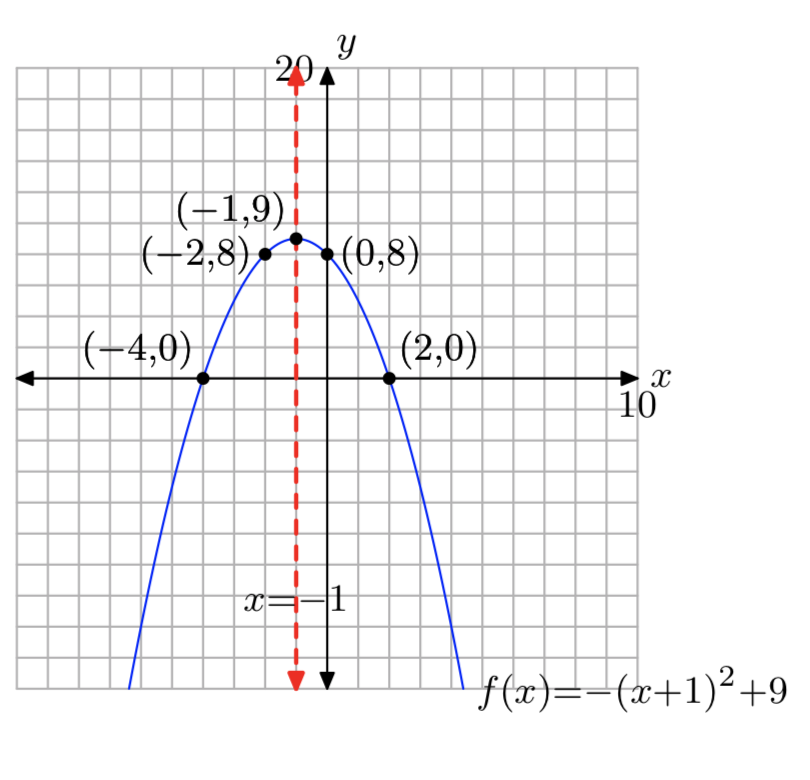
Вправа$\PageIndex{28}$

$f(x) = −x^2−2x+24$

Вправа$\PageIndex{29}$

$f(x) = −x^2−8x+48$

Відповідь

Домен = ($−\infty, \infty$), Діапазон = ($−\infty$, 64]

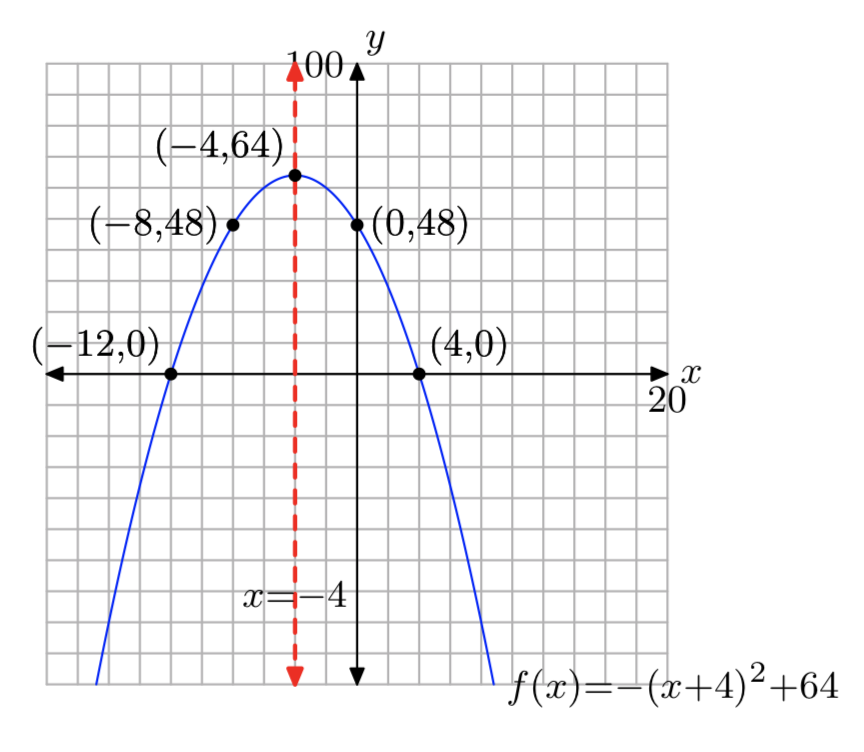
Вправа$\PageIndex{30}$

$f(x) = −x^2−8x+20$

У вправах 31 - 38 множник заданий квадратичний многочлен.

Вправа$\PageIndex{31}$

$42x^2+5x−2$

Відповідь

(7х+2) (6х−1)

Вправа$\PageIndex{32}$

$3x^2+7x−20$

Вправа$\PageIndex{33}$

$5x^2−19x+12$

Відповідь

(x−3) (5x−4)

Вправа$\PageIndex{34}$

$54x^2−3x−1$

Вправа$\PageIndex{35}$

$−4x^2+9x−5$

Відповідь

(4х−5) (−x+1)

Вправа$\PageIndex{36}$

$3x^2−5x−12$

Вправа$\PageIndex{37}$

$2x^2−3x−35$

Відповідь

(2х+7) (х−5)

Вправа$\PageIndex{38}$

$−6x^2+25x+9$

У вправах 39 - 46 знайти нулі заданих квадратичних функцій.

Вправа$\PageIndex{39}$

$f(x) = 2x^2−3x−20$

Відповідь

Нулі:$x = −\frac{5}{2}$, x = 4

Вправа$\PageIndex{40}$

$f(x) = 2x^2−7x−30$

Вправа$\PageIndex{41}$

$f(x) = −2x^2+x+28$

Відповідь

Нулі:$x = −\frac{7}{2}$, x = 4

Вправа$\PageIndex{42}$

$f(x) = −2x^2+15x−22$

Вправа$\PageIndex{43}$

$f(x) = 3x^2−20x+12$

Відповідь

Нулі:$x = \frac{2}{3}$, x = 6

Вправа$\PageIndex{44}$

$f(x) = 4x^2+11x−20$

Вправа$\PageIndex{45}$

$f(x) = −4x^2+4x+15$

Відповідь

Нулі:$x = −\frac{3}{2}$,$x = \frac{5}{2}$

Вправа$\PageIndex{46}$

$f(x) = −6x^2−x+12$

У Вправах 47 - 52 виконайте кожне з наступних завдань для заданих квадратичних функцій.

1. Завантажте функцію в Y1 Y= вашого графічного калькулятора. Налаштуйте параметри вікна так, щоб вершина була видна у вікні перегляду.
2. Налаштуйте систему координат на домашньому папері. Позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax. Зробіть розумну копію зображення у вікні перегляду вашого калькулятора на цій системі координат і позначте її рівнянням.
3. Використовуйте нульову утиліту на графічному калькуляторі, щоб знайти нулі функції. Використовуйте ці результати для побудови X-перехоплень у вашій системі координат та позначення їх координатами.
4. Використовуйте суворо алгебраїчну техніку (без калькулятора), щоб знайти нулі заданої квадратичної функції. Покажіть свою роботу поруч із вашою системою координат. Будьте вперті! Працюйте над проблемою, поки ваші алгебраїчні та графічно нулі не будуть розумним збігом.

Вправа$\PageIndex{47}$

$f(x) = 2x^2+3x−35$

Відповідь

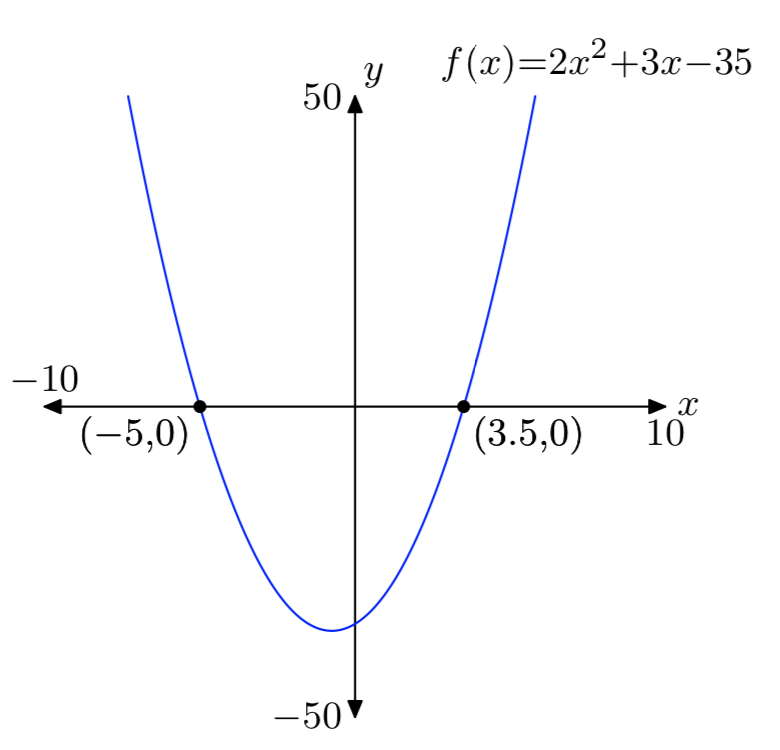
Вправа$\PageIndex{48}$

$f(x) = 2x^2−5x−42$

Вправа$\PageIndex{49}$

$f(x) = −2x^2+5x+33$

Відповідь

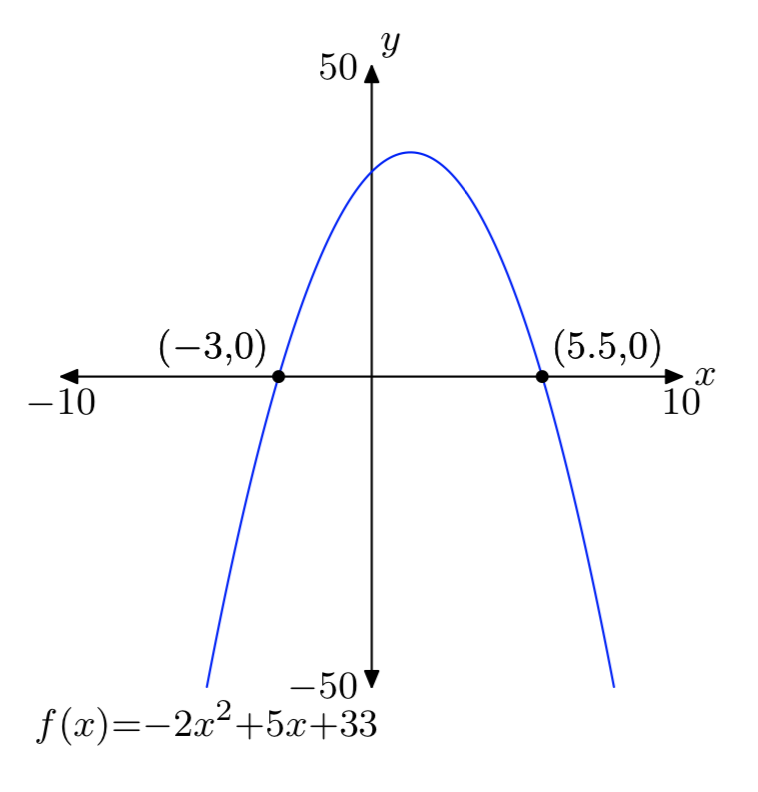
Вправа$\PageIndex{50}$

$f(x) = −2x^2−5x+52$

Вправа$\PageIndex{51}$

$f(x) = 4x^2−24x−13$

Відповідь

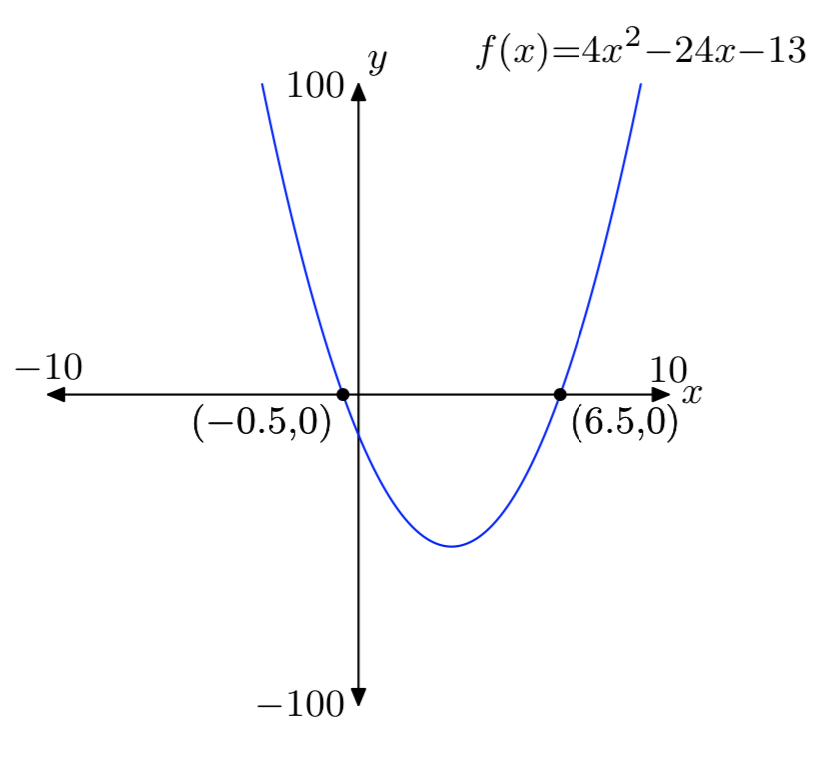
Вправа$\PageIndex{52}$

$f(x) = 4x^2+24x−45$

У Вправах 53 - 60 виконайте кожне з наступних завдань для заданих квадратичних функцій.

1. Налаштуйте систему координат на графічному папері. Позначте та масштабуйте кожну вісь. Не забудьте намалювати всі лінії лінійкою.
2. Використовуйте техніку завершення квадрата, щоб розмістити квадратичну функцію у вигляді вершини. Покладіть вершину на вашій системі координат і позначте її координатами. Намалюйте вісь симетрії на вашій системі координат і позначте її рівнянням.
3. Використовуйте строго алгебраїчний метод (без калькуляторів), щоб знайти x-перехоплення графа квадратичної функції. Покладіть їх на вашій системі координат і позначте їх координатами.
4. Знайти y-перехоплення графа квадратичної функції. Покладіть y-перехоплення на вашій системі координат та його дзеркальне відображення поперек осі симетрії, а потім позначте ці точки їх координатами.
5. Використовуючи всю побудовану інформацію, намалюйте графік квадратичної функції і позначте його вершинної формою її рівняння. Використовуйте інтервальне позначення для опису області та діапазону квадратичної функції.

Вправа$\PageIndex{53}$

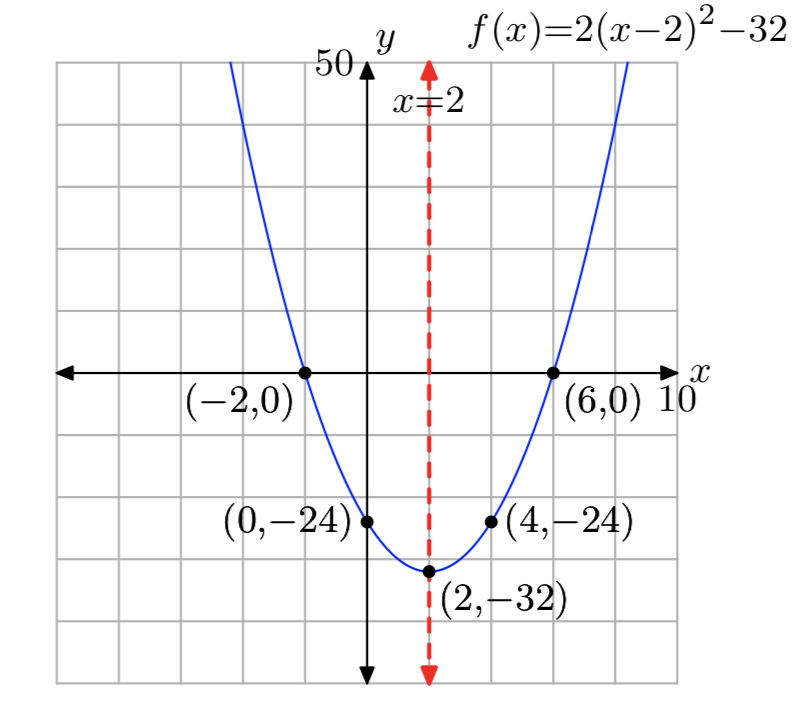
$f(x) = 2x^2−8x−24$

Відповідь

Домен = ($−\infty, \infty$), Діапазон = [−32,$\infty$)

Вправа$\PageIndex{54}$

$f(x) = 2x^2−4x−6$

Вправа$\PageIndex{55}$

$f(x) = −2x^2−4x+16$

Відповідь

Домен = ($−\infty, \infty$), Діапазон = ($−\infty$, 18]

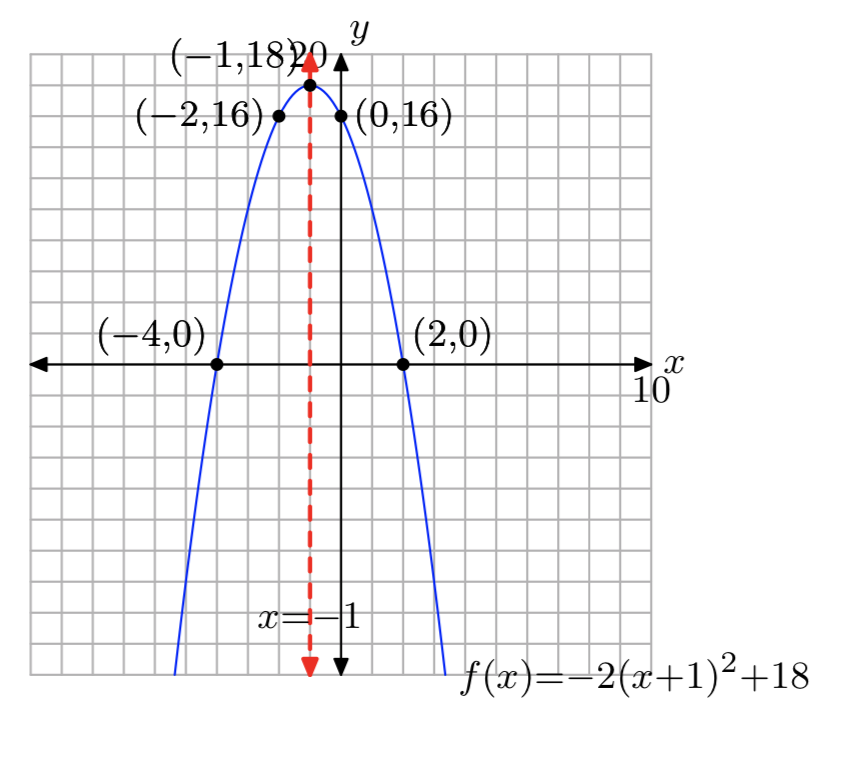
Вправа$\PageIndex{56}$

$f(x) = −2x^2−16x+40$

Вправа$\PageIndex{57}$

$f(x) = 3x^2+18x−48$

Відповідь

Домен = ($−\infty, \infty$), Діапазон = [−75,$\infty$)

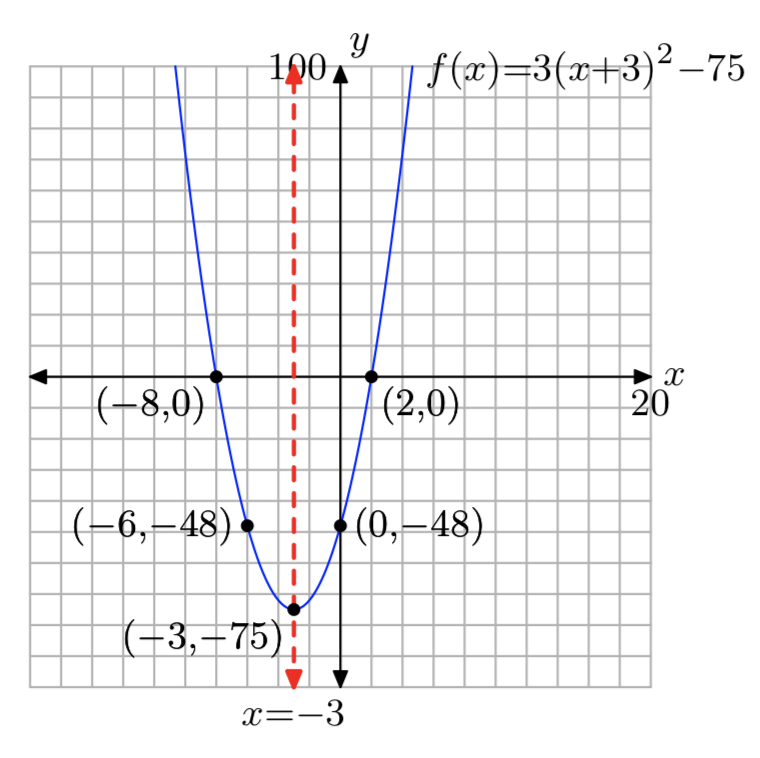
Вправа$\PageIndex{58}$

$f(x) = 3x^2+18x−216$

Вправа$\PageIndex{59}$

$f(x) = 2x^2+10x−48$

Відповідь

Домен = ($−\infty, \infty$), Діапазон = [−$\frac{121}{2}$,$\infty$)

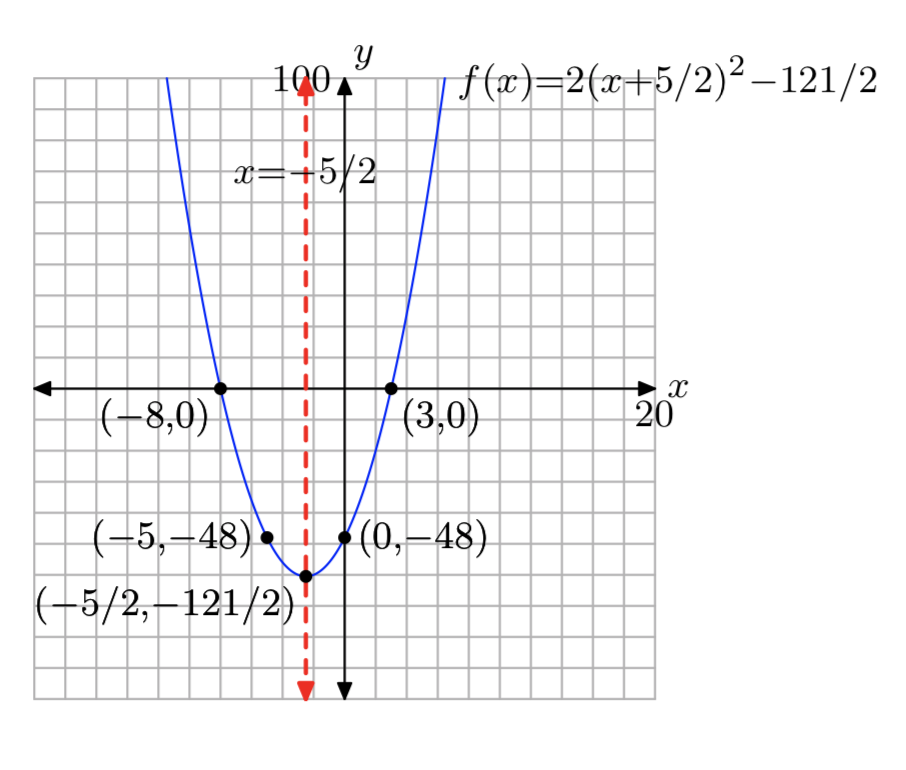
Вправа$\PageIndex{60}$

$f(x) = 2x^2−10x−100$

У вправах 61 - 66, Використовуйте графік$f(x) = ax^2+bx+c$ показаного, щоб знайти всі розв'язки рівняння f (x) = 0. (Примітка: кожне рішення є цілим числом.)

Вправа$\PageIndex{61}$

Відповідь

−2, 3

Вправа$\PageIndex{62}$

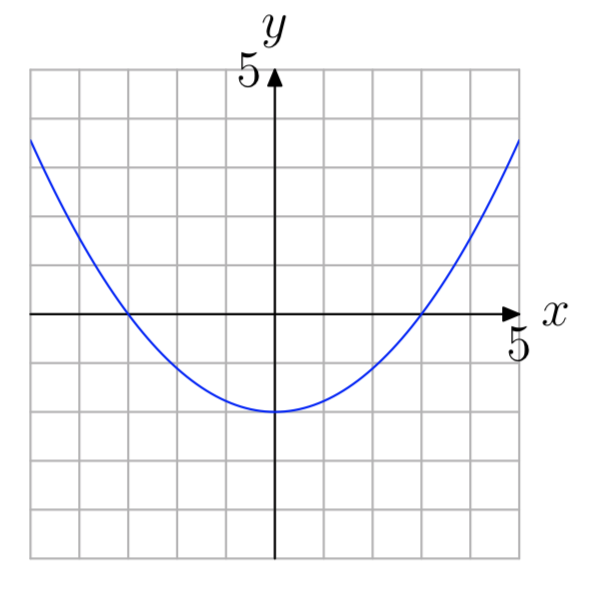
Вправа$\PageIndex{63}$

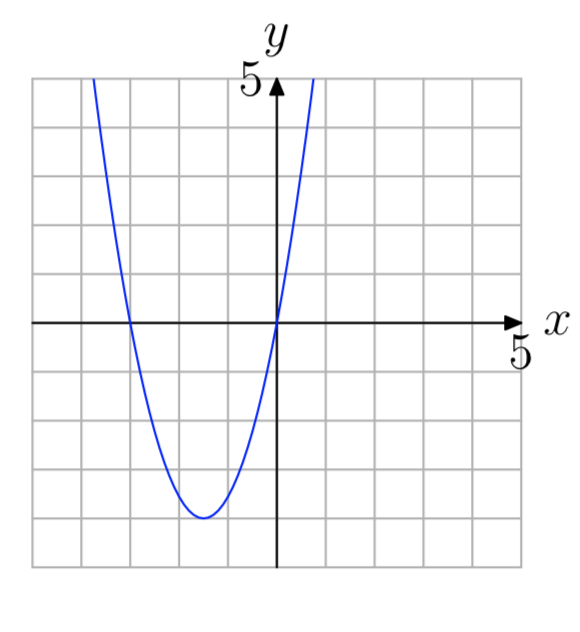
Відповідь

−3, 0

Вправа$\PageIndex{64}$

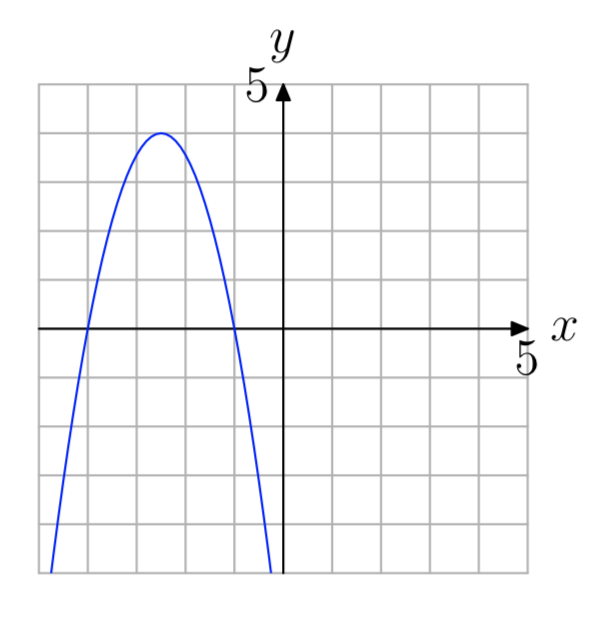
Вправа$\PageIndex{65}$

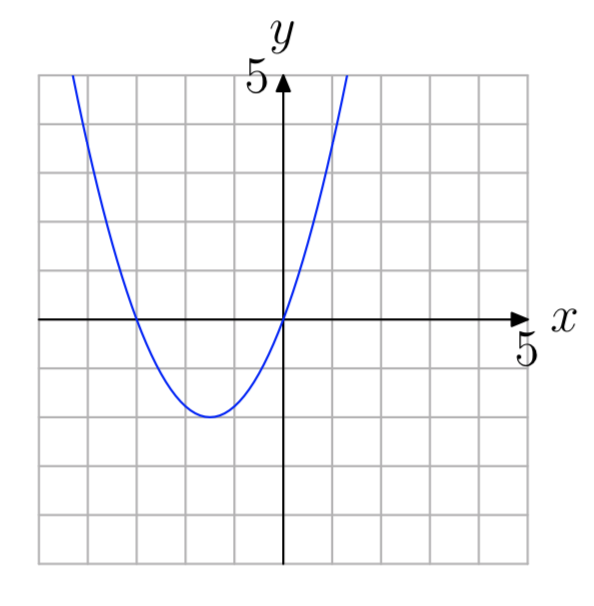
Відповідь

−3, 0

Вправа$\PageIndex{66}$