5.2: Вершинна форма
- Page ID
- 58067
У попередньому розділі ви дізналися, що ескіз графіка квадратичної функції є простим завданням, якщо він представлений у вигляді вершин.
\[f(x)=a(x-h)^{2}+k \nonumber \]
Мета поточного розділу - почати з найбільш загальної форми квадратичної функції, а саме
\[f(x)=a x^{2}+b x+c \nonumber \]
і маніпулювати рівнянням у формі вершини. Після того, як у вас є квадратична функція у формі вершини, техніка попереднього розділу повинна дозволити вам побудувати графік квадратичної функції. Однак перш ніж звернути увагу на завдання перетворення загальної квадратики в вершинну форму, нам потрібно переглянути необхідні алгебраїчні основи. Почнемо з огляду важливого алгебраїчного ярлика під назвою квадрат біном.
Квадратне біноміальне
Мономіал - це єдиний алгебраїчний термін, зазвичай побудований у вигляді добутку числа (званого коефіцієнтом) та однієї або декількох змінних, піднятих до невід'ємних інтегральних степеней, таких як\(-3 x^{2}\) або 14\(y^{3} z^{5}\). Ключова фраза тут - «єдиний термін». Біноміал - це алгебраїчна сума або різниця двох мономов (або членів), таких як\(x+2 y\) або\(3 a b^{2}-2 c^{3}\). Ключова фраза тут - «два терміни».
Щоб «квадрат біном», почніть з довільного біноміала, такого як a+b, потім помножте його на себе, щоб отримати його квадрат (a + b) (a + b), або, більш компактно,\((a+b)^{2}\). Ми можемо використовувати розподільну властивість, щоб розширити квадрат двочлена a + b.
\[\begin{aligned}(a+b)^{2} &=(a+b)(a+b) \\ &=a(a+b)+b(a+b) \\ &=a^{2}+a b+b a+b^{2} \end{aligned}\]
Оскільки ab = ba, ми можемо додати два середні умови, щоб прийти до наступного властивості.
Нерухомість 3
Квадрат двочлена a + b розширюється наступним чином.
\[(a+b)^{2}=a^{2}+2 a b+b^{2}\]
Приклад\(\PageIndex{1}\)
Розгорнути\((x+4)^{2}\)
Рішення
Ми могли б діяти наступним чином.
\[\begin{align*}(x+4)^{2} &=(x+4)(x+4) \\ &=x(x+4)+4(x+4) \\ &=x^{2}+4 x+4 x+16 \\ &=x^{2}+8 x+16 \end{align*}\]
Хоча і правильна, ця методика не допоможе нам з нашою майбутньою задачею. Що нам потрібно зробити, це слідувати алгоритму, запропонованому Property 3.
Алгоритм квадратизації біноміалу
Щоб зробити квадрат двочлена a + b, дійте наступним чином:
- Квадратний перший термін, щоб отримати\(a^2\).
- Перше і друге члени помножте разом, а потім помножте результат на два, щоб отримати 2ab.
- Квадратний другий член, щоб отримати\(b^2\).
Таким чином, щоб розширити\((x + 4)^2\), слід поступити наступним чином.
- Квадратний перший термін, щоб отримати\(x^2\)
- Помножте перший і другий члени разом, а потім помножте на два, щоб отримати 8x.
- Квадратний другий член, щоб вийшло 16.
Продовження таким чином дозволяє виконати розширення подумки і просто записати рішення.
\[(x+4)^{2}=x^{2}+2(x)(4)+4^{2}=x^{2}+8 x+16 \nonumber\]
Ось ще кілька прикладів. У кожному ми написали додатковий крок, який допоможе уточнити процедуру. На практиці слід просто записати рішення без будь-яких проміжних кроків.
\[\begin{array}{l}{(x+3)^{2}=x^{2}+2(x)(3)+3^{2}=x^{2}+6 x+9} \\ {(x-5)^{2}=x^{2}+2(x)(-5)+(-5)^{2}=x^{2}-10 x+25} \\ {\left(x-\frac{1}{2}\right)^{2}=x^{2}+2(x)\left(-\frac{1}{2}\right)+\left(-\frac{1}{2}\right)^{2}=x^{2}-x+\frac{1}{4}}\end{array}\]
Обов'язково ви освоїте цей ярлик, перш ніж перейти до решти матеріалу в цьому розділі.
Ідеальні квадратні триноміали
Після того, як ви освоїли квадрат біноміального, як в
\[(a+b)^{2}=a^{2}+2 a b+b^{2} \nonumber\]
це проста справа, щоб визначити і фактор триноми (три терміни), що мають форму\(a^{2}+2 a b+b^{2}\). Ви просто «скасуєте» множення. Всякий раз, коли ви помічаєте тріноміал, перший і третій члени якого є ідеальними квадратами, ви повинні підозрювати, що це впливає наступним чином.
\[a^{2}+2 a b+b^{2}=(a+b)^{2} \nonumber\]
Триноміал, який впливає відповідно до цього правила або шаблону, називається ідеальним квадратним тріноміалом.
Наприклад, перший і останній члени наступного триноміала - ідеальні квадрати.
\[x^{2}+16 x+64 \nonumber\]
Квадратні коріння першого і останнього членів - х і 8 відповідно. Значить, має сенс спробувати наступне.
\[x^{2}+16 x+64=(x+8)^{2} \nonumber\]
Важливо, щоб ви перевіряли свій результат за допомогою множення. Отже, слідуючи триступінчастому алгоритму квадратизації біноміального:
- Квадрат х, щоб отримати\(x^2\).
- Помножте x і 8, щоб отримати 8x, потім помножте цей результат на 2, щоб отримати 16x.
- Квадрат 8, щоб отримати 64.
Отже,\(x^2 + 16x + 64\) це ідеальний квадратний триноміал і фактори як\((x + 8)^2\).
Як ще один приклад розглянемо\(x^2 − 10x + 25\). Квадратні коріння першого і останнього членів - х і 5 відповідно. Значить, має сенс спробувати
\[x^{2}-10 x+25=(x-5)^{2} \nonumber\]
Знову ж таки, слід перевірити цей результат. Зверніть увагу, що подвоєний добуток x та −5 дорівнює середньому члену ліворуч, а саме −10x.
Завершення площі
Якщо квадратична функція задана у формі вершини, це проста справа, щоб намалювати параболу, представлену рівнянням. Для прикладу розглянемо квадратичну функцію
\[f(x)=(x+2)^{2}+3\]
який знаходиться у формі вершини. Графік цього рівняння являє собою параболу, яка відкривається вгору. Він перекладається 2 одиниці вліво і 3 одиниці вгору. У цьому і полягає перевага вершинної форми. Перетворення, необхідні для малювання графіка функції, легко помітити, коли рівняння записано у формі вершини.
Це проста справа, щоб\(f(x) = (x + 2)^2 + 3\) перетворити рівняння в загальну форму квадратичної функції,\(f(x) = ax^2 + bx + c\). Ми просто використовуємо триступінчастий алгоритм для квадратного біноміального; потім ми об'єднуємо як терміни.
\[\begin{array}{l}{f(x)=(x+2)^{2}+3} \\ {f(x)=x^{2}+4 x+4+3} \\ {f(x)=x^{2}+4 x+7}\end{array}\]
Однак зауважте, що результат цієї маніпуляції не настільки корисний\(f(x) = x^2 + 4x+ 7\), як вершинна форма, оскільки важко визначити перетворення, необхідні для малювання параболи, представленої рівнянням\(f(x) = x^2 + 4x + 7\).
Це дійсно зворотне маніпуляції вище, що потрібно. Якщо нам представлено рівняння у формі\(f(x) = ax^2 + bx + c\), наприклад\(f(x) = x^2 + 4x + 7\), то для перетворення цього рівняння у форму вершини потрібен алгебраїчний метод\(f(x) = a(x−h)^2+k\); або в цьому випадку назад до початкової форми вершини\(f(x) = (x + 2)^2 + 3\).
Процедура, яку ми шукаємо, називається завершенням квадрата. Назва походить від того, що нам потрібно «завершити» тріноміал з правого боку,\(y = x^2 + 4x + 7\) щоб він став ідеальним квадратним триноміалом.
Алгоритм завершення квадрата
Процедура виконання каре передбачає три ключових етапи.
- Візьміть половину коефіцієнта х і квадратний результат.
- Складіть і відніміть величину з першого кроку, щоб права частина рівняння не змінилася.
- Порахуйте отриманий квадрат ідеальним триноміалом і комбінуйте постійні терміни.
Простежимо за цією процедурою і розмістимо\(f(x) = x^2 + 4x + 7\) у вигляді вершини.
- Візьміть половину коефіцієнта х. таким чином, (1/2) (4) = 2. Квадратний цей результат. Таким чином,\(2^2 = 4\).
- Додайте і відніміть 4 у правій частині рівняння\(f(x) = x^2 + 4x + 7\)\[f(x)=x^{2}+4 x+4-4+7\]
- Згрупуйте перші три члени праворуч. Вони утворюють ідеальний квадратний тріноміал.
\[f(x)=\left(x^{2}+4 x+4\right)-4+7 \nonumber\]
Тепер вважайте ідеальний квадратний триноміал і об'єднайте константи в кінці, щоб отримати
\[f(x)=(x+2)^{2}+3 \nonumber\]
Ось і все, ми закінчили! Ми повернули загальну квадратичну\(f(x) = x^2 + 4x + 7\) назад до вершинної форми\(f(x) = (x + 2)^2 + 3\).
Спробуємо ще раз.
Приклад\(\PageIndex{2}\)
Помістіть квадратичну функцію\(f(x) = x^2 − 8x − 9\) у вигляді вершини.
Рішення
Слідуємо триетапному алгоритму виконання квадрата.
- Візьмемо половину коефіцієнта х і квадрат: т. Е.\[[(1 / 2)(-8)]^{2}=[-4]^{2}=16 \nonumber\]
- Додайте і відніміть цю суму в праву частину функції. \[f(x)=x^{2}-8 x+16-16-9 \nonumber\]
- Згрупуйте перші три члени праворуч. Вони утворюють ідеальний квадратний тріноміал. \[f(x)=\left(x^{2}-8 x+16\right)-16-9 \nonumber\]
Порахуйте ідеальний квадратний триноміал і об'єднайте коефіцієнти в кінці.
\[f(x)=(x-4)^{2}-25 \nonumber\]
Тепер давайте подивимося, як ми можемо використовувати техніку завершення квадрата, щоб допомогти у малюванні графіків загальних квадратичних функцій.
Робота з\(f(x) = x^2 + bx + c\)
Приклади в цьому розділі матимуть вигляд\(f(x) = x^2 + bx + c\). Зверніть увагу, що коефіцієнт\(x^2\) дорівнює 1. У наступному розділі ми будемо працювати з більш жорсткою формою\(f(x) = ax^2 + bx + c\), де\(a \neq 1\).
Приклад\(\PageIndex{3}\)
Заповніть квадрат, щоб розмістити\(f(x) = x^2 + 6x + 2\) у формі вершини та намалюйте його графік.
Рішення
Спочатку візьміть половину коефіцієнта х і квадрат; т\([(1/2)(6)]^2 = 9\). Е. У правій частині рівняння складіть і відніміть цю величину, щоб не змінювати рівняння.
\[f(x)=x^{2}+6 x+9-9+2 \nonumber\]
Згрупуйте перші три члени праворуч.
\[f(x)=\left(x^{2}+6 x+9\right)-9+2 \nonumber\]
Перші три терміни з правого боку утворюють ідеальний квадратний триноміал, який легко враховується. Також з'єднайте константи в кінці.
\[f(x)=(x+3)^{2}-7 \nonumber\]
Це парабола, яка відкривається вгору. Нам потрібно зрушити параболу на 3 одиниці вліво, а потім на 7 одиниць вниз, розмістивши вершину в (−3, −7), як показано на малюнку\(\PageIndex{1}\) (a). Віссю симетрії є вертикальною лінією x = −3. Таблиця на малюнку\(\PageIndex{1}\) (б) обчислює дві точки праворуч від осі симетрії, а дзеркальні точки зліва від осі симетрії роблять для точної ділянки параболи.
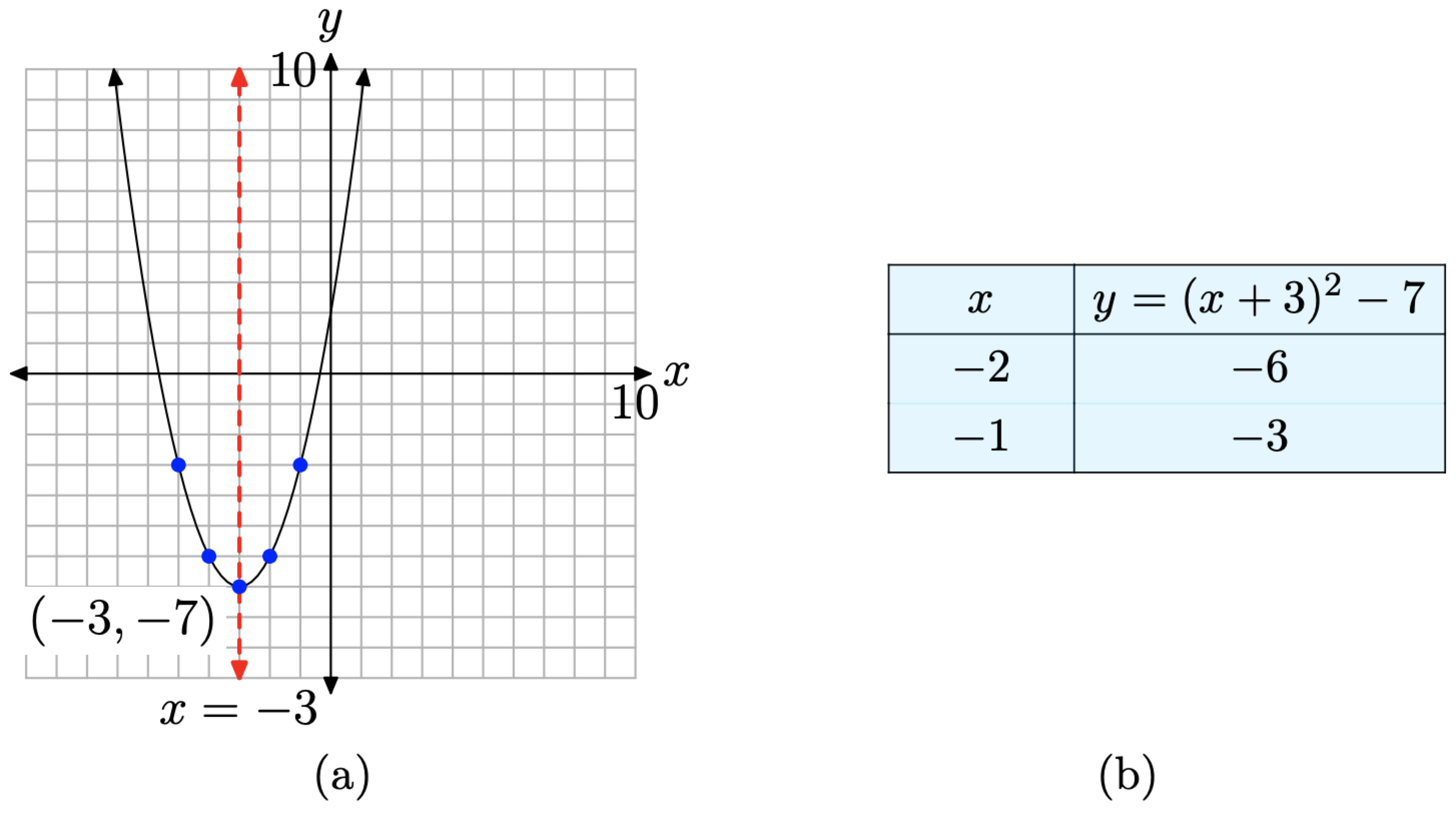
Давайте розглянемо інший приклад.
Приклад\(\PageIndex{4}\)
Заповніть квадрат, щоб розмістити\(f(x) = x^2 − 8x + 21\) у формі вершини та намалюйте його графік.
Рішення
Спочатку візьміть половину коефіцієнта х і квадрат; т\([(1/2)(−8)]^2 = 16\). Е. У правій частині рівняння складіть і відніміть цю величину, щоб не змінювати рівняння.
\[f(x)=x^{2}-8 x+16-16+21 \nonumber\]
Згрупуйте перші три члени в правій частині рівняння.
\[f(x)=\left(x^{2}-8 x+16\right)-16+21 \nonumber\]
Перші три терміни утворюють ідеальний квадратний триноміал, який легко враховується. Також комбінуйте константи в кінці.
\[f(x)=(x-4)^{2}+5 \nonumber\]
Це парабола, яка відкривається вгору. Нам потрібно зрушити параболу 4 одиниці вправо, а потім 5 одиниць вгору, розмістивши вершину на (4, 5), як показано на малюнку\(\PageIndex{2}\) (а). Таблиця на малюнку\(\PageIndex{2}\) (б) обчислює дві точки праворуч від осі симетрії, а дзеркальні точки зліва від осі симетрії роблять для точної ділянки параболи.
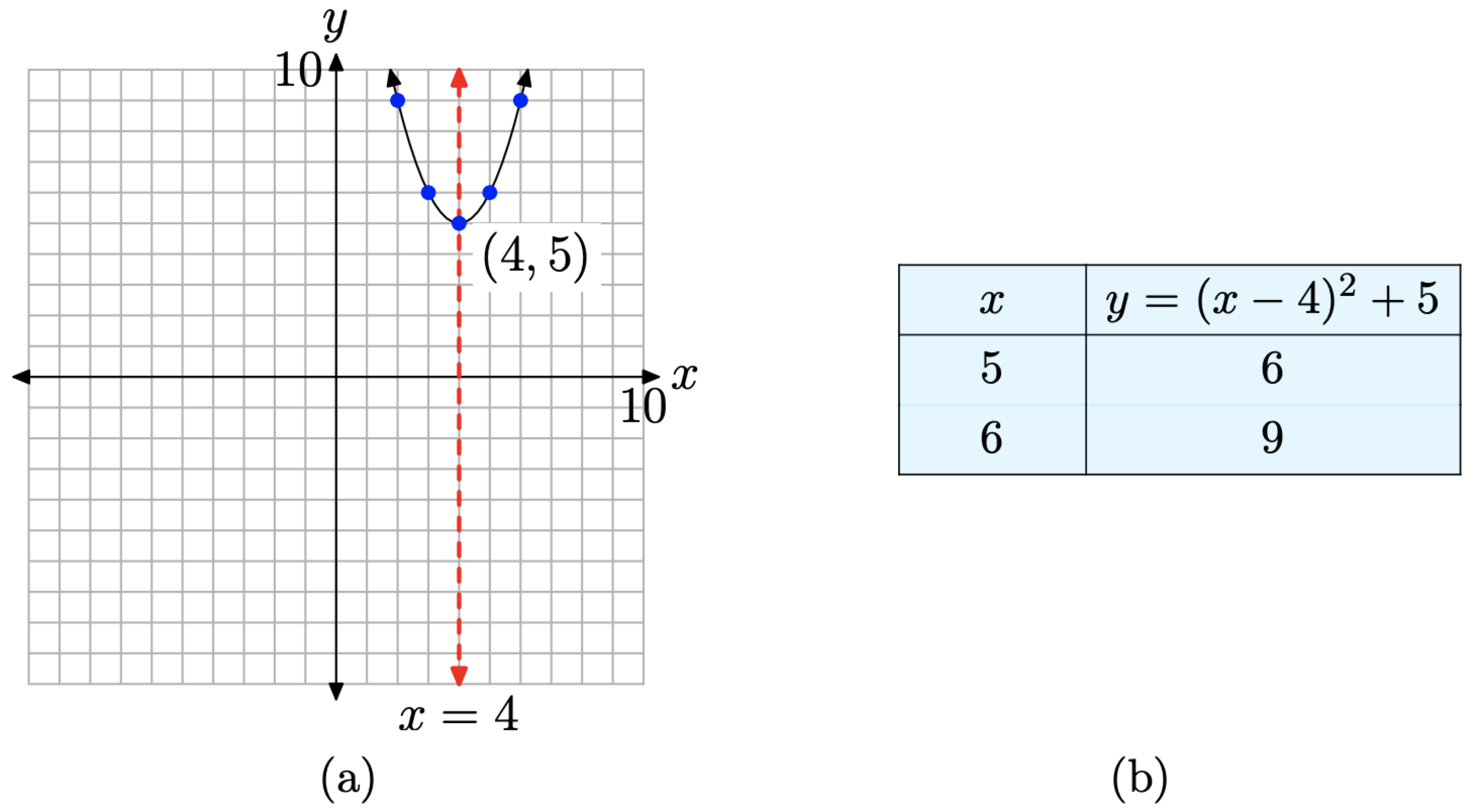
Робота з\(f(x) = ax^2 + bx + c\)
В останніх двох прикладах коефіцієнт\(x^2\) дорівнював 1. У цьому розділі ми дізнаємося, як завершити квадрат, коли коефіцієнт\(x^2\) дорівнює деякому числу, відмінному від 1.
Приклад\(\PageIndex{5}\)
Заповніть квадрат, щоб розмістити\(f(x)=2 x^{2}+4 x-4\) у формі вершини та намалюйте його графік.
Рішення
В останніх двох прикладах ми отримали деяку міру успіху, коли коефіцієнт\(x^2\) становив 1. Ми просто освоювалися з цією ситуацією, і ми хотіли б продовжувати бути зручними, так що давайте почнемо з факторингу 2 з кожного члена на правій стороні рівняння.
\[f(x)=2\left[x^{2}+2 x-2\right] \nonumber\]
Якщо ми ігноруємо множник 2 поза спереду, коефіцієнт\(x^2\) в триноміальному виразі всередині дужок дорівнює 1. Ах, знайома земля! Ми будемо діяти так, як ми робили раніше, але ми будемо нести коефіцієнт 2 поза дужками на кожному кроці. Почніть з взяття половини коефіцієнта х і зведення результату в квадрат; т\([(1/2)(2)]^2 = 1\). Е.
Додайте і відніміть цю суму всередині дужок, щоб не змінювати рівняння.
\[f(x)=2\left[x^{2}+2 x+1-1-2\right] \nonumber\]
Згрупуйте перші три члени всередині дужок і об'єднайте константи.
\[f(x)=2\left[\left(x^{2}+2 x+1\right)-3\right] \nonumber\]
Згруповані терміни всередині дужок утворюють ідеальний квадратний триноміал, який легко враховується.
\[f(x)=2\left[(x+1)^{2}-3\right] \nonumber\]
Нарешті, перерозподіліть 2.
\[f(x)=2(x+1)^{2}-6 \nonumber\]
Це парабола, яка відкривається вгору. Крім того, він розтягується в 2 рази, тому буде дещо вужче, ніж наші попередні приклади. Параболу також зміщують на 1 одиницю вліво, потім на 6 одиниць вниз, розміщуючи вершину в (−1, −6), як показано на малюнку\(\PageIndex{3}\) (а). Таблиця на малюнку\(\PageIndex{3}\) (б) обчислює дві точки праворуч від осі симетрії, а дзеркальні точки зліва від осі симетрії роблять для точної ділянки параболи.
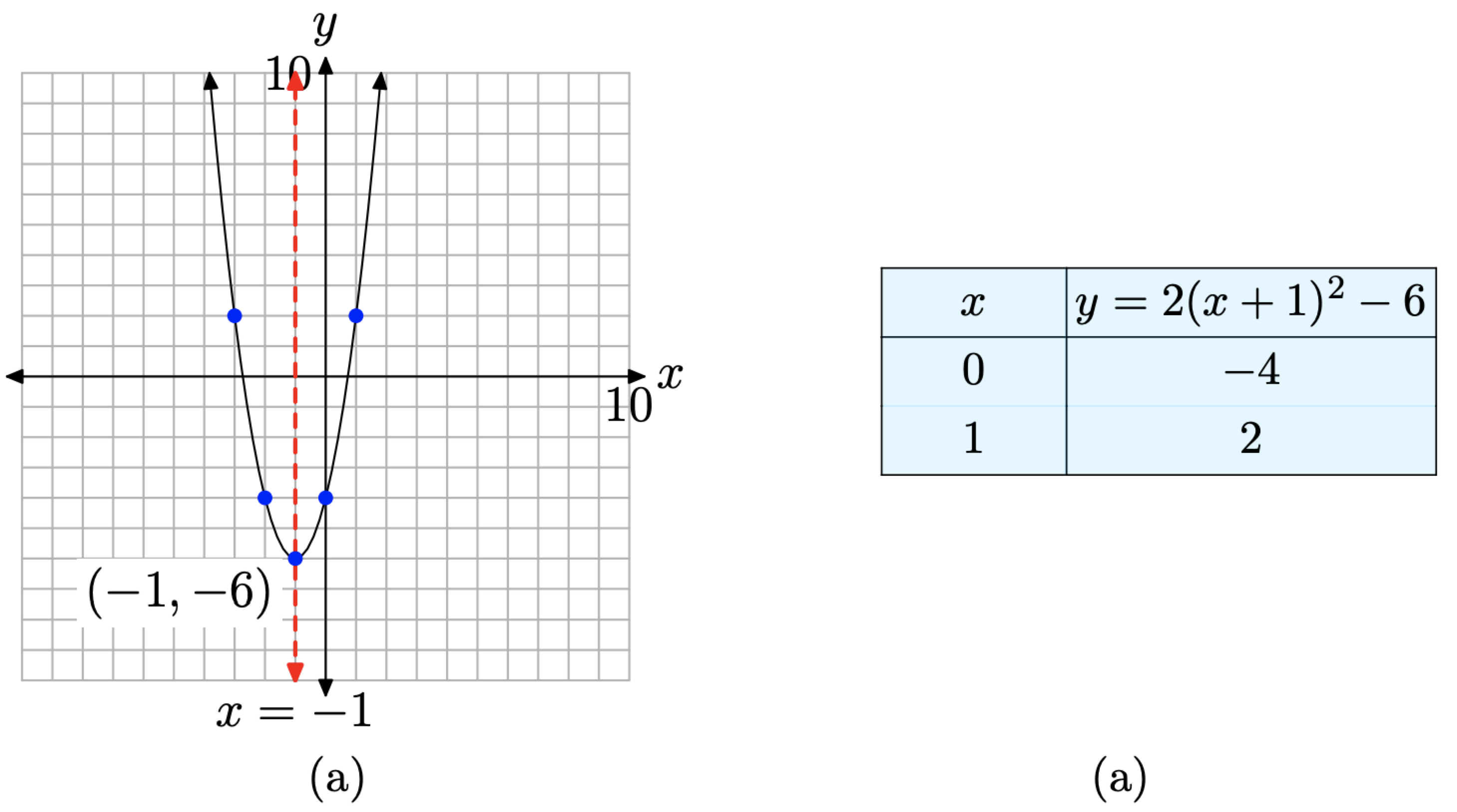
Давайте розглянемо приклад, де коефіцієнт від\(x^2\) негативний.
Приклад\(\PageIndex{6}\)
Заповніть квадрат, щоб розмістити\(f(x) = −x^2 + 6x − 2\) у формі вершини та намалюйте його графік.
Рішення
В останньому прикладі ми врахували коефіцієнт\(x^2\). Це залишило нам триноміал, який має провідний коефіцієнт 1, який дозволив нам діяти так само, як ми робили раніше: вдвічі зменшити середній коефіцієнт і квадрат, додати і відняти цю суму, коефіцієнт отриманого ідеального квадратного триноміала. Оскільки ми досягли успіху з цією методикою в останньому прикладі, давайте почнемо знову з факторингу провідного коефіцієнта, в даному випадку a −1.
\[f(x)=-1\left[x^{2}-6 x+2\right] \nonumber\]
Якщо проігнорувати коефіцієнт −1 поза фронтом, коефіцієнт\(x^2\) у триноміальному виразі всередині дужок дорівнює 1. Знову знайома земля! Ми будемо діяти так, як ми робили раніше, але ми будемо переносити коефіцієнт −1 поза дужками на кожному кроці. Почніть з взяття половини коефіцієнта х і зведення результату в квадрат; т\([(1/2)(−6)]^2 = 9\). Е.
Додайте і відніміть цю суму всередині дужок, щоб не змінювати рівняння.
\[f(x)=-1\left[x^{2}-6 x+9-9+2\right] \nonumber\]
Згрупуйте перші три члени всередині дужок і об'єднайте константи.
\[f(x)=-1\left[\left(x^{2}-6 x+9\right)-7\right] \nonumber\]
Згруповані терміни всередині дужок утворюють ідеальний квадратний триноміал, який легко враховується.
\[f(x)=-1\left[(x-3)^{2}-7\right] \nonumber\]
Нарешті, перерозподіліть −1.
\[f(x)=-(x-3)^{2}+7 \nonumber\]
Це парабола, яка відкривається вниз. Параболу також зміщують на 3 одиниці вправо, потім на 7 одиниць вгору, розміщуючи вершину на (3, 7), як показано на малюнку\(\PageIndex{4}\) (а). Таблиця на малюнку\(\PageIndex{4}\) (б) обчислює дві точки праворуч від осі симетрії, а дзеркальні точки зліва від осі симетрії роблять для точної ділянки параболи.
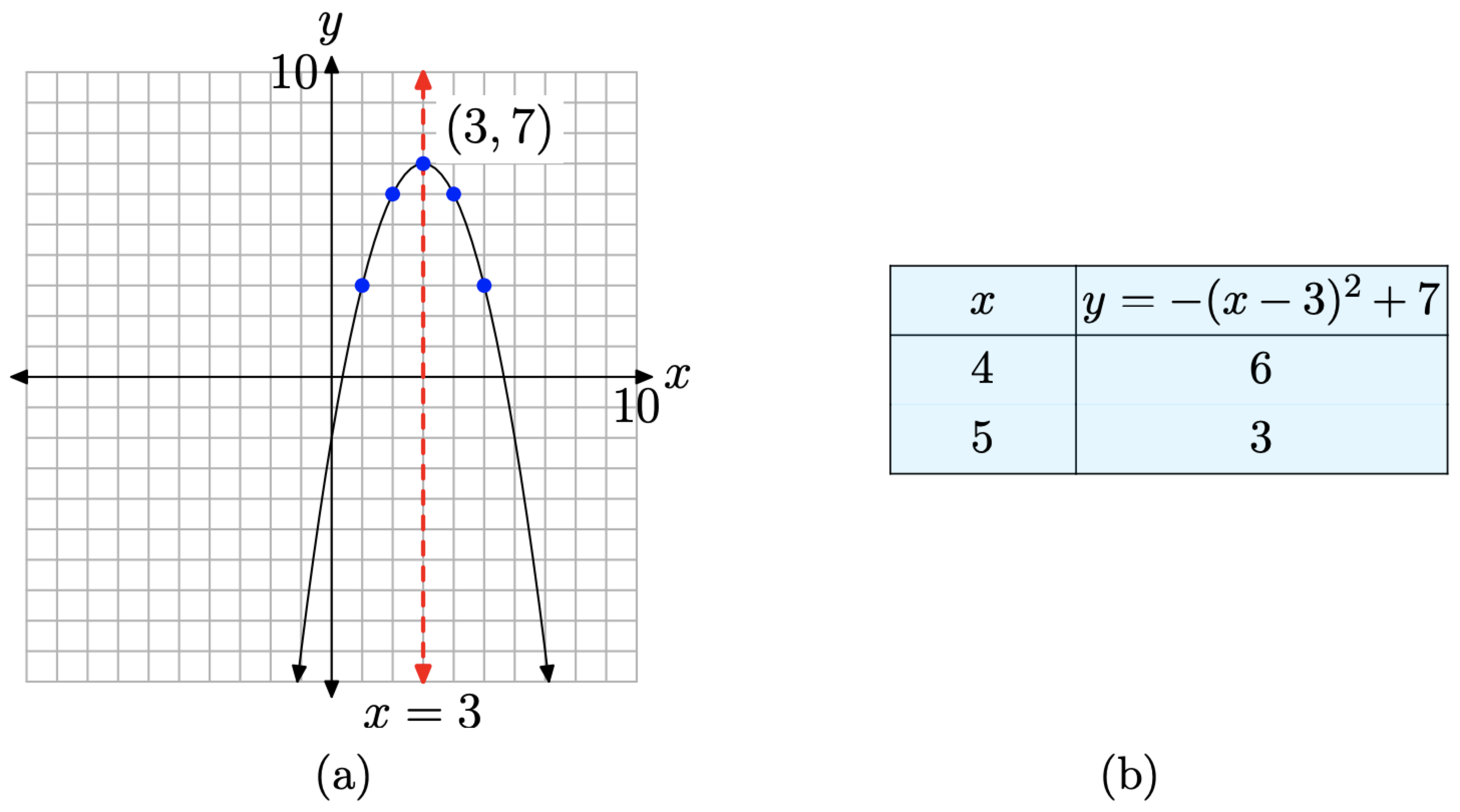
Спробуємо ще один приклад.
Приклад\(\PageIndex{7}\)
Заповніть квадрат, щоб розмістити\(f(x) = 3x^2 + 4x − 8\) у формі вершини та намалюйте його графік.
Рішення
Почнемо знову з факторингу провідного коефіцієнта, в даному випадку a 3.
\[f(x)=3\left[x^{2}+\frac{4}{3} x-\frac{8}{3}\right] \nonumber\]
Дроби додають ступінь складності, але, якщо ви будете дотримуватися тієї ж процедури, що і в попередніх прикладах, ви повинні мати можливість отримати необхідний результат. Візьміть половину коефіцієнта х і квадратний результат; т\([(1/2)(4/3)]^2 = [2/3]^2 = 4/9\). Е.
Додайте і відніміть цю суму всередині дужок, щоб не змінювати рівняння.
\[f(x)=3\left[x^{2}+\frac{4}{3} x+\frac{4}{9}-\frac{4}{9}-\frac{8}{3}\right] \nonumber\]
Групуйте перші три члени всередині дужок. Вам знадобиться спільний знаменник, щоб об'єднати константи.
\[f(x)=3\left[\left(x^{2}+\frac{4}{3} x+\frac{4}{9}\right)-\frac{4}{9}-\frac{24}{9}\right] \nonumber\]
Згруповані терміни всередині дужок утворюють ідеальний квадратний триноміал, який легко враховується.
\[f(x)=3\left[\left(x+\frac{2}{3}\right)^{2}-\frac{28}{9}\right] \nonumber\]
Нарешті, перерозподіліть 3.
\[f(x)=3\left(x+\frac{2}{3}\right)^{2}-\frac{28}{3} \nonumber\]
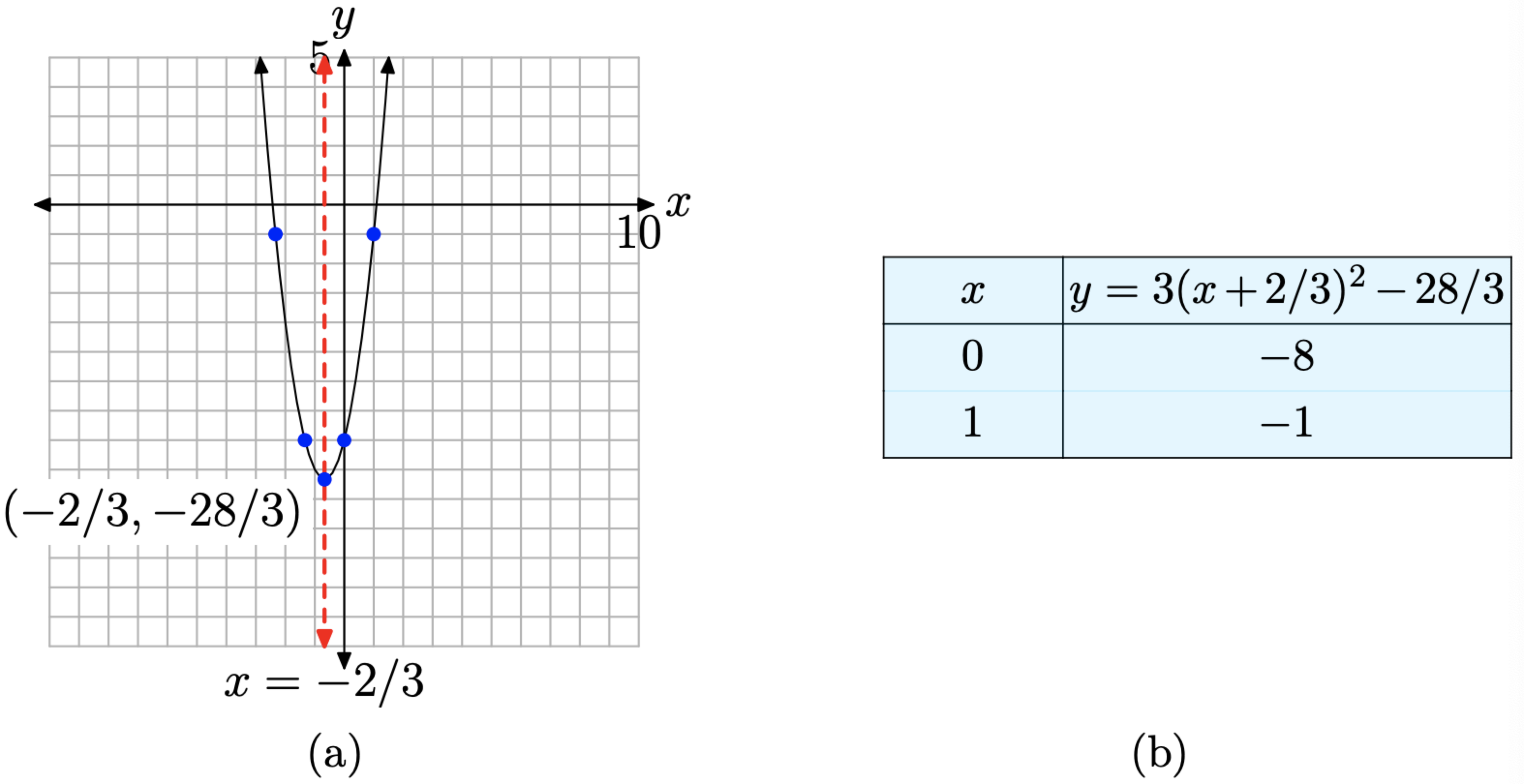
Це парабола, яка відкривається вгору. Вона також розтягується в 3 рази, тому буде вужче, ніж всі наші попередні приклади. Параболу також зміщують на 2/3 одиниць вліво, потім на 28/3 одиниці вниз, розміщуючи вершину в (−2/3, −28/3), як показано на малюнку\(\PageIndex{5}\) (а). Таблиця на малюнку\(\PageIndex{5}\) (б) обчислює дві точки праворуч від осі симетрії, а дзеркальні точки зліва від осі симетрії роблять для точної ділянки параболи.
Вправа
У вправах 1 - 8 розширити біном.
Вправа\(\PageIndex{1}\)
\((x+\frac{4}{5})^2\)
- Відповідь
-
\(x^2+\frac{8}{5}x+\frac{16}{25}\)
Вправа\(\PageIndex{2}\)
\((x−\frac{4}{5})^2\)
Вправа\(\PageIndex{3}\)
\((x+3)^2\)
- Відповідь
-
\(x^2+6x+9\)
Вправа\(\PageIndex{4}\)
\((x+5)^2\)
Вправа\(\PageIndex{5}\)
\((x−7)^2\)
- Відповідь
-
\(x^2−14x+49\)
Вправа\(\PageIndex{6}\)
\((x−\frac{2}{5})^2\)
Вправа\(\PageIndex{7}\)
\((x−6)^2\)
- Відповідь
-
\(x^2−12x+36\)
Вправа\(\PageIndex{8}\)
\((x−\frac{5}{2})^2\)
У вправах 9 - 16, фактор ідеальний квадратний триноміал.
Вправа\(\PageIndex{9}\)
\(x^2−\frac{6}{5}x+\frac{9}{25}\)
- Відповідь
-
\((x−\frac{3}{5})^2\)
Вправа\(\PageIndex{10}\)
\(x^2+5x+\frac{25}{4}\)
Вправа\(\PageIndex{11}\)
\(x^2−12x+36\)
- Відповідь
-
\((x−6)^2\)
Вправа\(\PageIndex{12}\)
\(x^2+3x+\frac{9}{4}\)
Вправа\(\PageIndex{13}\)
\(x^2+12x+36\)
- Відповідь
-
\((x+6)^2\)
Вправа\(\PageIndex{14}\)
\(x^2−\frac{3}{2}x+\frac{9}{16}\)
Вправа\(\PageIndex{15}\)
\(x^2+18x+81\)
- Відповідь
-
\((x+9)^2\)
Вправа\(\PageIndex{16}\)
\(x^2+10x+25\)
У Вправах 17 - 24 перетворіть задану квадратичну функцію у форму вершини,\(f(x) = (x−h)^2+k\) заповнивши квадрат.
Вправа\(\PageIndex{17}\)
\(f(x) = x^2−x+8\)
- Відповідь
-
\((x−\frac{1}{2})^2+\frac{31}{4}\)
Вправа\(\PageIndex{18}\)
\(f(x) = x^2+x−7\)
Вправа\(\PageIndex{19}\)
\(f(x) = x^2−5x−4\)
- Відповідь
-
\((x−\frac{5}{2})^2−\frac{41}{4}\)
Вправа\(\PageIndex{20}\)
\(f(x) = x^2+7x−1\)
Вправа\(\PageIndex{21}\)
\(f(x) = x^2+2x−6\)
- Відповідь
-
\((x+1)^2−7\)
Вправа\(\PageIndex{22}\)
\(f(x) = x^2+4x+8\)
Вправа\(\PageIndex{23}\)
\(f(x) = x^2−9x+3\)
- Відповідь
-
\((x−\frac{9}{2})−\frac{69}{4}\)
Вправа\(\PageIndex{24}\)
\(f(x) = x^2−7x+8\)
У Вправах 25 - 32 перетворіть задану квадратичну функцію у форму вершини,\(f(x) = a(x−h)^2+k\) заповнивши квадрат.
Вправа\(\PageIndex{25}\)
\(f(x) = −2x^2−9x−3\)
- Відповідь
-
\(−2(x+\frac{9}{4})^2+\frac{57}{8}\)
Вправа\(\PageIndex{26}\)
\(f(x) = −4x^2−6x+1\)
Вправа\(\PageIndex{27}\)
\(f(x) = 5x^2+5x+5\)
- Відповідь
-
\(5(x+\frac{1}{2})^2+\frac{15}{4}\)
Вправа\(\PageIndex{28}\)
\(f(x) = 3x^2−4x−6\)
Вправа\(\PageIndex{29}\)
\(f(x) = 5x^2+7x−3\)
- Відповідь
-
\(5(x+\frac{7}{10})^2−\frac{109}{20}\)
Вправа\(\PageIndex{30}\)
\(f(x) = 5x^2+6x+4\)
Вправа\(\PageIndex{31}\)
\(f(x) = −x^2−x+4\)
- Відповідь
-
\(−1(x+\frac{1}{2})^2+\frac{17}{4}\)
Вправа\(\PageIndex{32}\)
\(f(x) = −3x^2−6x+4\)
У вправах 33 - 38 знайти вершину графа заданої квадратичної функції.
Вправа\(\PageIndex{33}\)
\(f(x) = −2x^2+5x+3\)
- Відповідь
-
\((\frac{5}{4}, \frac{49}{8})\)
Вправа\(\PageIndex{34}\)
\(f(x) = x^2+5x+8\)
Вправа\(\PageIndex{35}\)
\(f(x) = −4x^2−4x+1\)
- Відповідь
-
\((−\frac{1}{2}, 2)\)
Вправа\(\PageIndex{36}\)
\(f(x) = 5x^2+7x+8\)
Вправа\(\PageIndex{37}\)
\(f(x) = 4x^2+2x+8\)
- Відповідь
-
\((−\frac{1}{4}, \frac{31}{4})\)
Вправа\(\PageIndex{38}\)
\(f(x) = x^2+x−7\)
У вправах 39 - 44 знайти вісь симетрії графіка заданої квадратичної функції.
Вправа\(\PageIndex{39}\)
\(f(x) = −5x^2−7x−8\)
- Відповідь
-
\(x = −\frac{7}{10}\)
Вправа\(\PageIndex{40}\)
\(f(x) = x^2+6x+3\)
Вправа\(\PageIndex{41}\)
\(f(x) = −2x^2−5x−8\)
- Відповідь
-
\(x = −\frac{5}{4}\)
Вправа\(\PageIndex{42}\)
\(f(x) = −x^2−6x+2\)
Вправа\(\PageIndex{43}\)
\(f(x) = −5x^2+x+6\)
- Відповідь
-
\(x = \frac{1}{10}\)
Вправа\(\PageIndex{44}\)
\(f(x) = x^2−9x−6\)
Для кожної з квадратичних функцій у Вправах 45 - 66 виконайте кожне з наступних завдань.
- Використовуйте техніку завершення квадрата, щоб розмістити задану квадратичну функцію у вигляді вершини.
- Налаштуйте систему координат на аркуші графічного паперу. Позначте та масштабуйте кожну вісь.
- Намалюйте вісь симетрії і позначте її рівнянням. Покладіть вершину і позначте її координатами.
- Налаштуйте таблицю біля вашої системи координат, яка обчислює координати двох точок по обидві сторони від осі симетрії. Помістіть ці точки і їх дзеркальне відображення поперек осі симетрії. Намалюйте параболу і позначте її рівнянням
- Використовуйте графік параболи для визначення області та діапазону квадратичної функції. Опишіть домен і діапазон за допомогою інтервальних позначень.
Вправа\(\PageIndex{45}\)
\(f(x) = x^2−8x+12\)
- Відповідь
-
\(f(x) = (x−4)^2−4\)
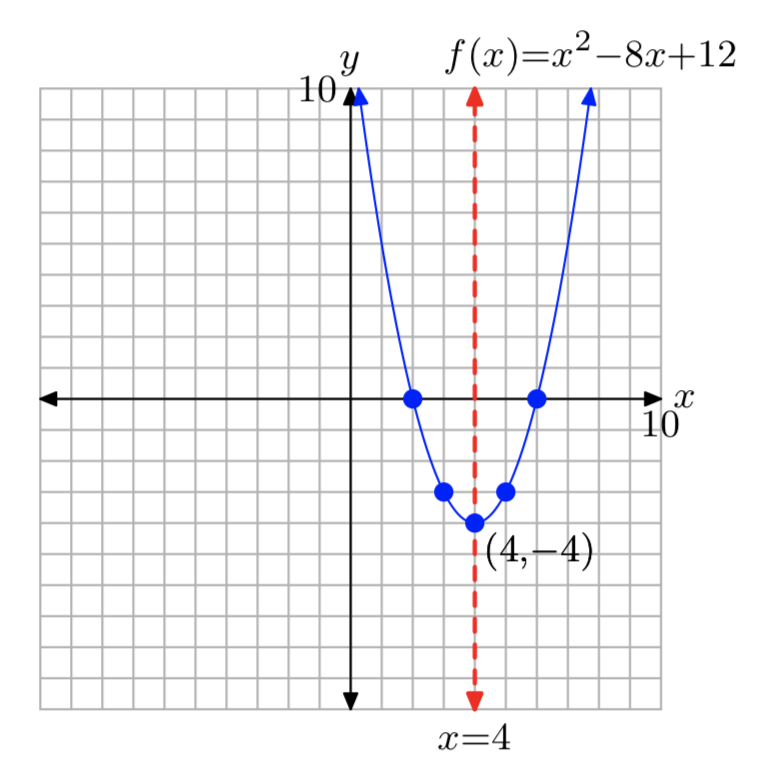
Домен =\(\mathbb{R}\), Діапазон = [−4,\(\infty\))
Вправа\(\PageIndex{46}\)
\(f(x) = x^2+4x−1\)
Вправа\(\PageIndex{47}\)
\(f(x) = x^2+6x+3\)
- Відповідь
-
\(f(x) = (x+3)^2−6\)
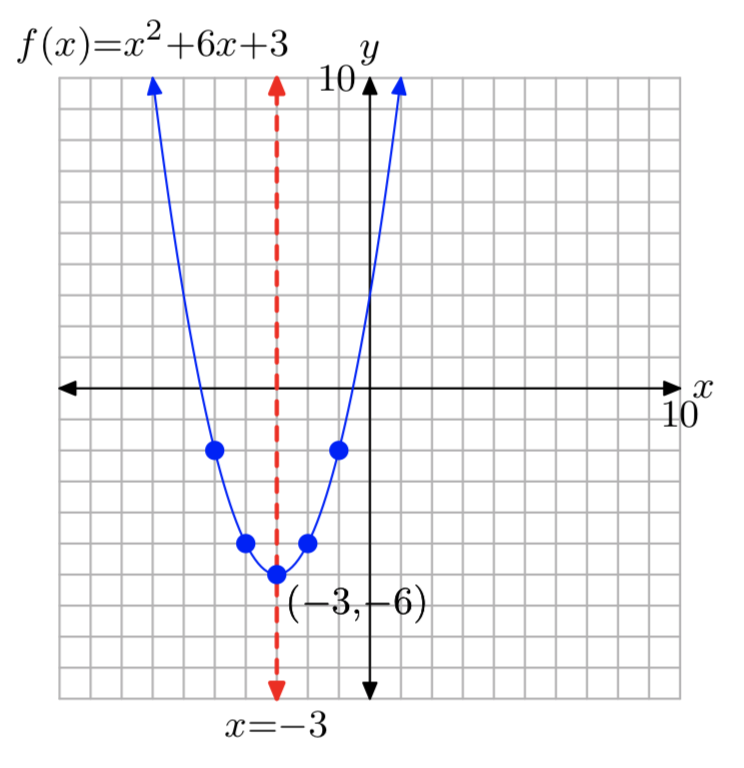
Домен =\(\mathbb{R}\), Діапазон = [−6,\(\infty\))
Вправа\(\PageIndex{48}\)
\(f(x)=x^2−4x+1\)
Вправа\(\PageIndex{49}\)
\(f(x) = x^2−2x−6\)
- Відповідь
-
\(f(x) = (x−1)^2−7\)
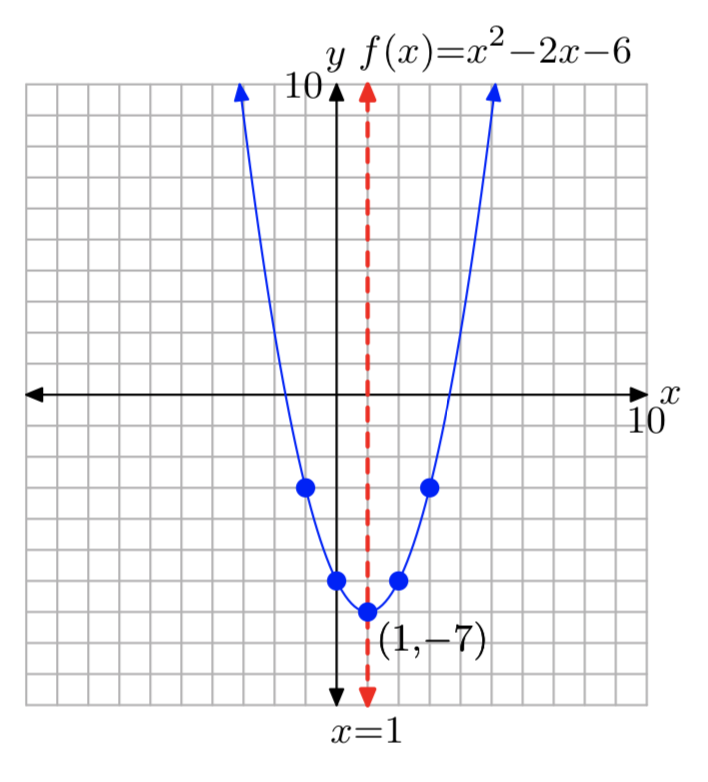
Домен =\(\mathbb{R}\), Діапазон = [−7,\(\infty\))
Вправа\(\PageIndex{50}\)
\(f(x) = x^2+10x+23\)
Вправа\(\PageIndex{51}\)
\(f(x) = −x^2+6x−4\)
- Відповідь
-
\(f(x) = −(x−3)^2+5\)
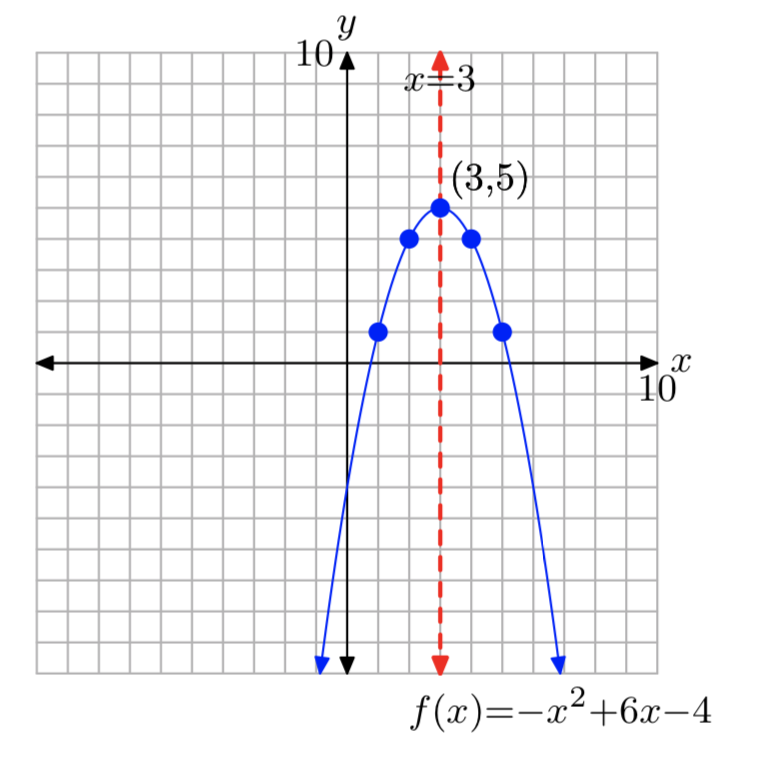
Домен =\(\mathbb{R}\), Діапазон = (−\(\infty\), 5]
Вправа\(\PageIndex{52}\)
\(f(x) = −x^2−6x−3\)
Вправа\(\PageIndex{53}\)
\(f(x) = −x^2−10x−21\)
- Відповідь
-
\(f(x) = −(x+5)^2+4\)
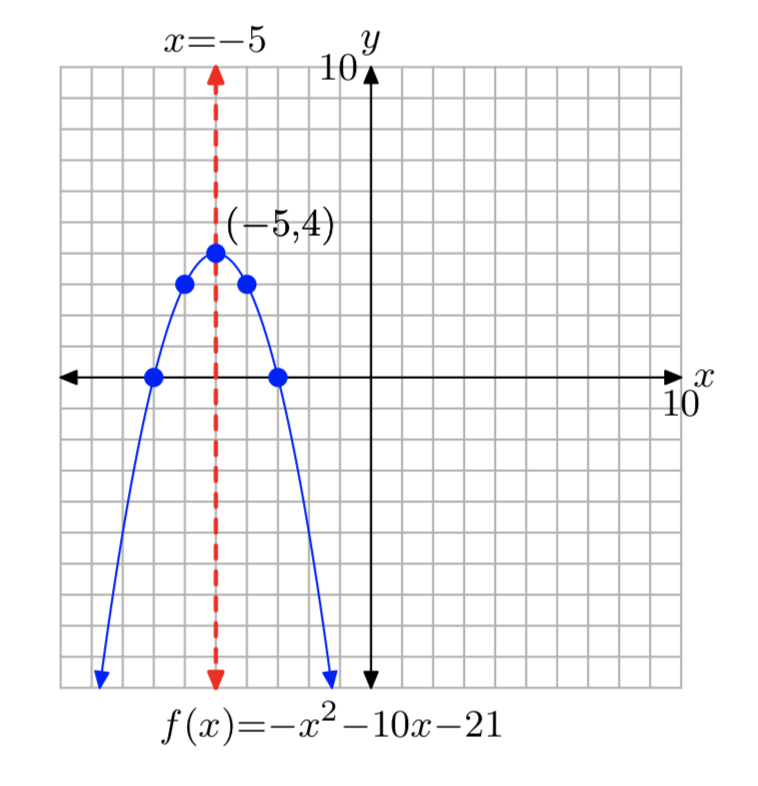
Домен =\(\mathbb{R}\), Діапазон = (−\(\infty\), 4]
Вправа\(\PageIndex{54}\)
\(f(x) = −x^2+12x−33\)
Вправа\(\PageIndex{55}\)
\(f(x) = 2x^2−8x+3\)
- Відповідь
-
\(f(x) = 2(x−2)^2−5\)
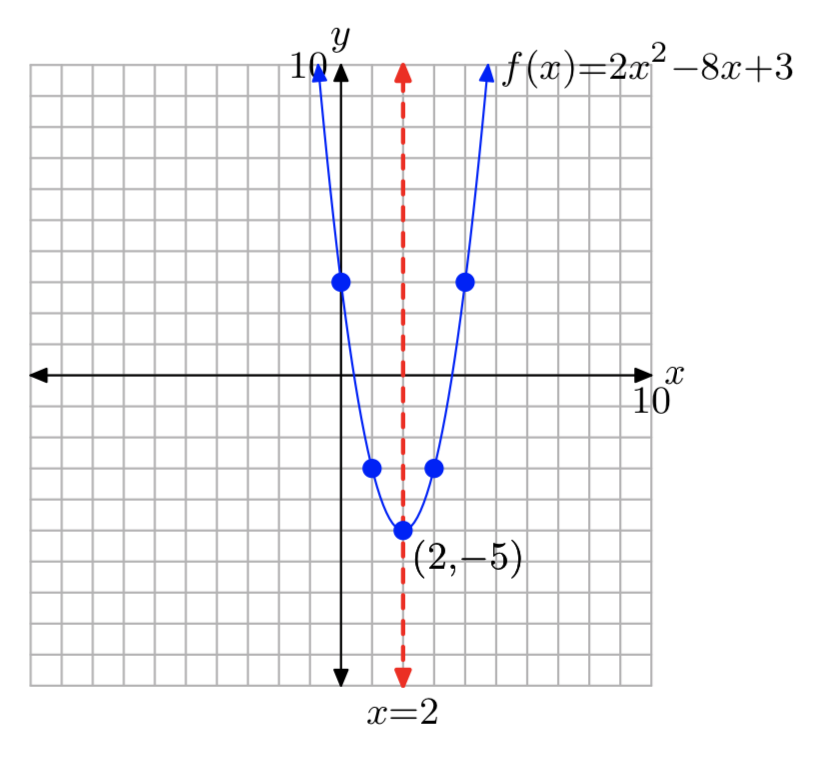
Домен =\(\mathbb{R}\), Діапазон = [−5,\(\infty\))
Вправа\(\PageIndex{56}\)
\(f(x) = 2x^2+8x+4\)
Вправа\(\PageIndex{57}\)
\(f(x) = −2x^2−12x−13\)
- Відповідь
-
\(f(x) = −2(x+3)^2+5\)
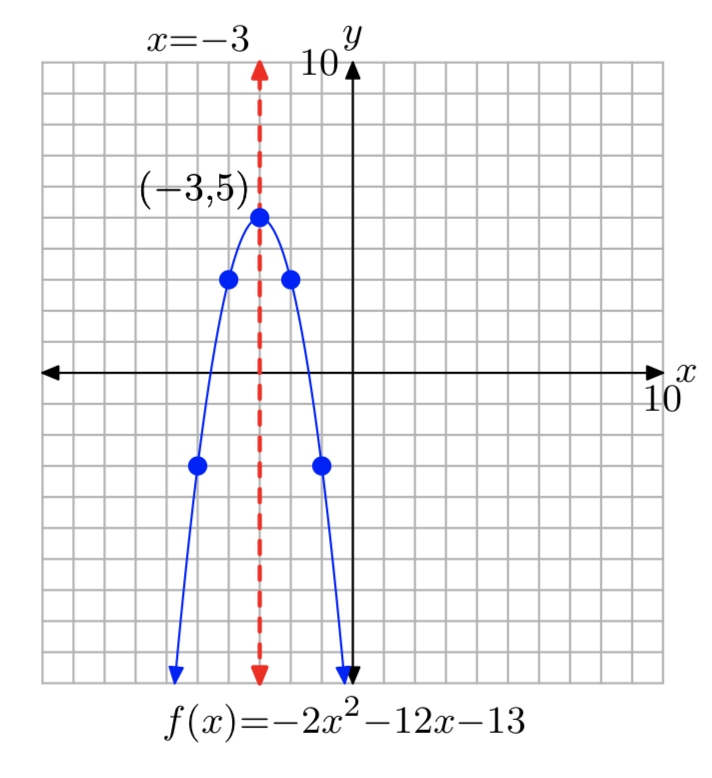
Домен =\(\mathbb{R}\), Діапазон = (−\(\infty\), 5]
Вправа\(\PageIndex{58}\)
\(f(x) = −2x^2+24x−70\)
Вправа\(\PageIndex{59}\)
\(f(x) = \frac{1}{2}x^2−4x+5\)
- Відповідь
-
\(f(x) = \frac{1}{2}(x−4)^2−3\)
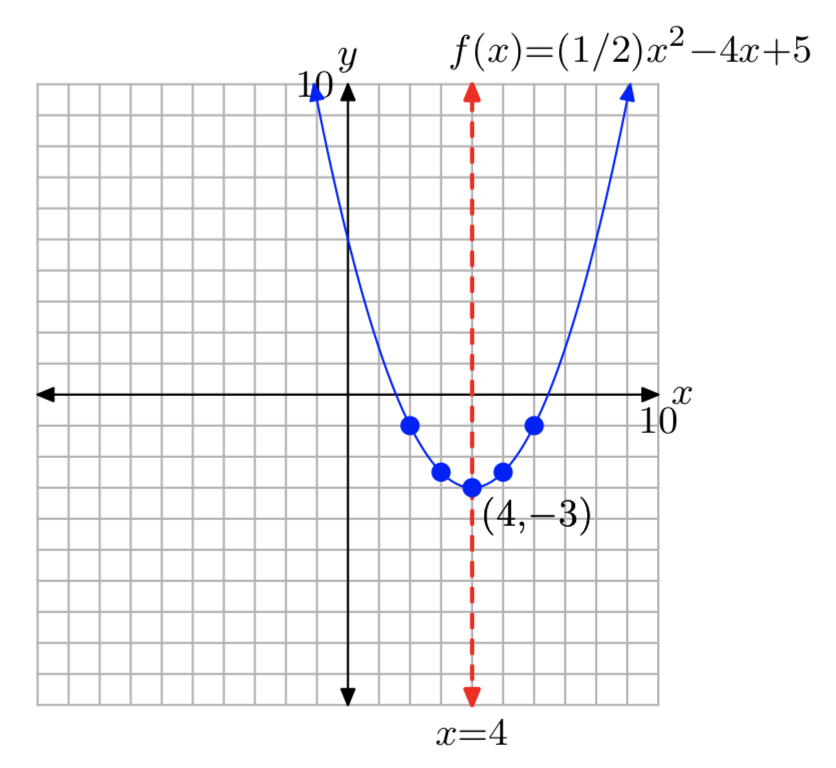
Домен =\(\mathbb{R}\), Діапазон = [−3,\(\infty\))
Вправа\(\PageIndex{60}\)
\(f(x) = \frac{1}{2}x^2+4x+6\)
Вправа\(\PageIndex{61}\)
\(f(x) = −\frac{1}{2}x^2−3x+\frac{1}{2}\)
- Відповідь
-
\(f(x) = −\frac{1}{2}(x+3)^2+5\)
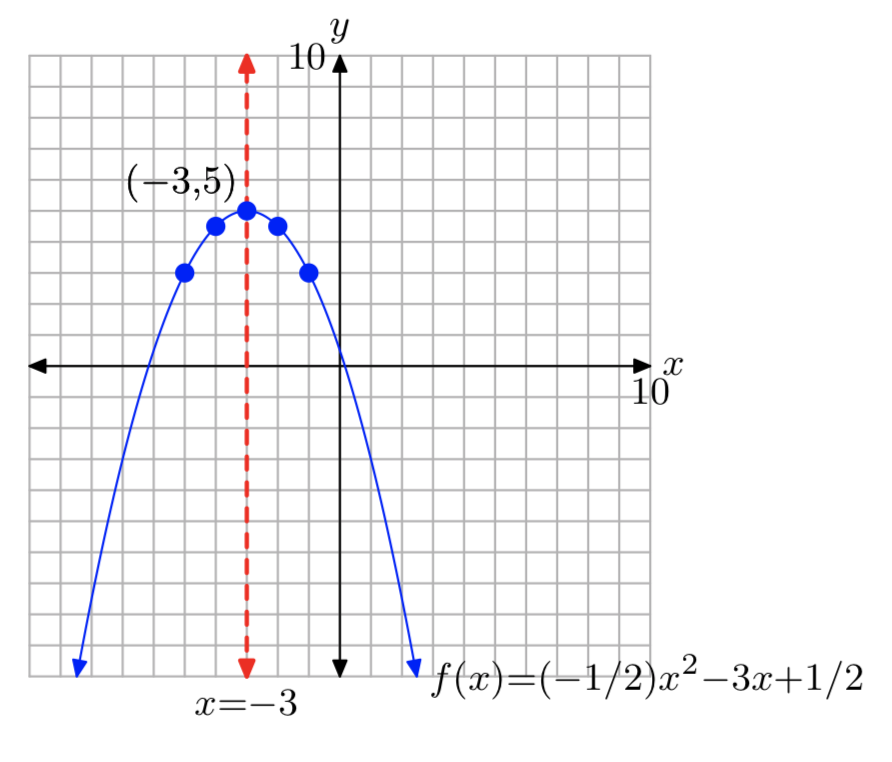
Домен =\(\mathbb{R}\), Діапазон = (−\(\infty\), 5]
Вправа\(\PageIndex{62}\)
\(f(x) = −\frac{1}{2}x^2+4x−2\)
Вправа\(\PageIndex{63}\)
\(f(x) = 2x^2+7x−2\)
- Відповідь
-
\(f(x) = 2(x+\frac{7}{4})^2− \frac{65}{8}\)
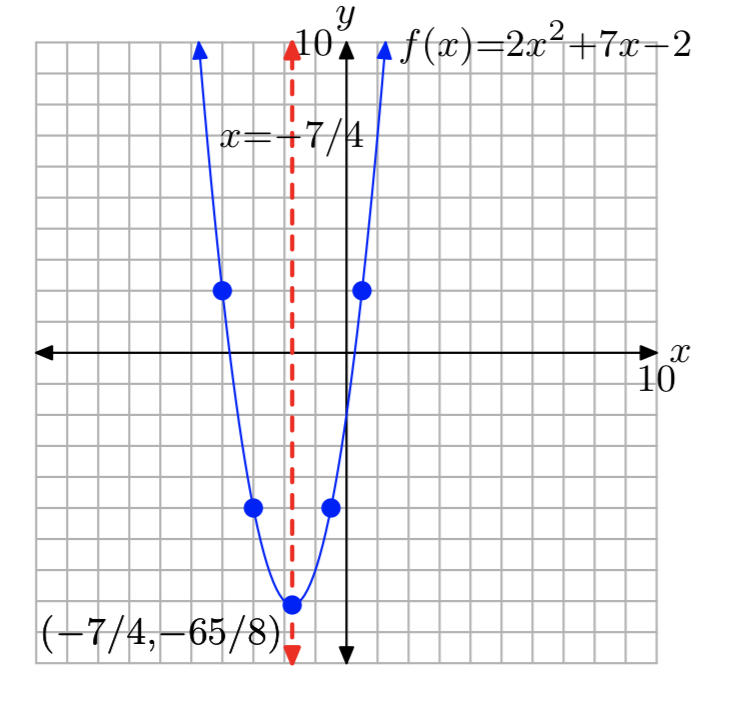
Домен =\(\mathbb{R}\), Діапазон = [\(−\frac{65}{8}\),\(\infty\))
Вправа\(\PageIndex{64}\)
\(f(x) = −2x^2−5x−4\)
Вправа\(\PageIndex{65}\)
\(f(x) = −3x^2+8x−3\)
- Відповідь
-
\(f(x) = −3(x−\frac{4}{3})^2+\frac{7}{3}\)
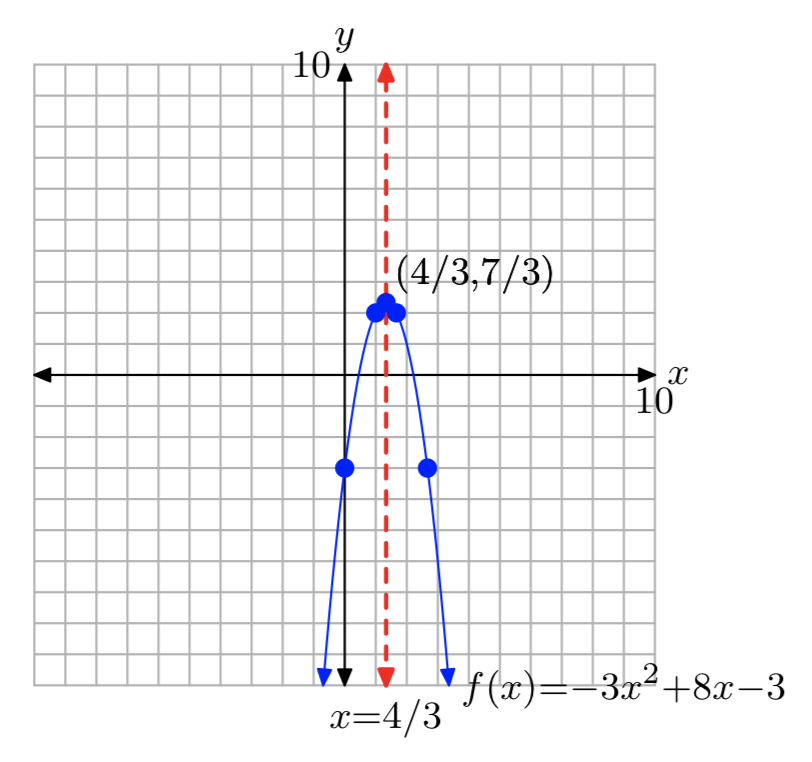
Домен =\(\mathbb{R}\), Діапазон = (−\(\infty\),\(\frac{7}{3}\)]
Вправа\(\PageIndex{66}\)
\(f(x) = 3x^2+4x−6\)
У Вправах 67 - 72 знайти діапазон заданої квадратичної функції. Висловлюйте свою відповідь в обох інтервалах і встановлених позначеннях.
Вправа\(\PageIndex{67}\)
\(f(x) = −2x^2+4x+3\)
- Відповідь
-
(\(−\infty\), 5] = {x|\(x \le 5\)}
Вправа\(\PageIndex{68}\)
\(f(x) = x^2+4x+8\)
Вправа\(\PageIndex{69}\)
\(f(x) = 5x^2+4x+4\)
- Відповідь
-
[\(\frac{16}{5}\),\(\infty\)) = {x|\(x \ge 5\)}
Вправа\(\PageIndex{70}\)
\(f(x) = 3x^2−8x+3\)
Вправа\(\PageIndex{71}\)
\(f(x) = −x^2−2x−7\)
- Відповідь
-
(\(−\infty\), −6] = {x|\(x \le −6\)}
Вправа\(\PageIndex{72}\)
\(f(x) = x^2+x+9\)
Дриль для майстерності. У вправах 73 - 76 оцініть функцію при заданому значенні b.
Вправа\(\PageIndex{73}\)
\(f(x) = 9x^2−9x+4\); б = −6
- Відповідь
-
382
Вправа\(\PageIndex{74}\)
\(f(x) = −12x^2+5x+2\); б = −3
Вправа\(\PageIndex{75}\)
\(f(x) = 4x^2−6x−4\); б = 11
- Відповідь
-
414
Вправа\(\PageIndex{76}\)
\(f(x) = −2x^2−11x−10\); б = −12
Дриль для майстерності. У вправах 77 - 80 оцініть функцію за заданим виразом.
Вправа\(\PageIndex{77}\)
Оцініть f (x+4) якщо\(f(x) = −5x^2+4x+2\).
- Відповідь
-
\(−5x^2−36x−62\)
Вправа\(\PageIndex{78}\)
Оцінити f (−4x−5), якщо\(f(x) = 4x^2+x+1\).
Вправа\(\PageIndex{79}\)
Оцінити f (4x−1), якщо\(f(x) = 4x^2+3x−3\).
- Відповідь
-
\(64x^2−20x−2\)
Вправа\(\PageIndex{80}\)
Оцінити f (−5x−3), якщо\(f(x) = −4x^2+x+4\).
