5.4: Квадратична формула

Розглянемо загальну квадратичну функцію $$f(x)=a x^{2}+b x+c$$

У попередньому розділі ми дізналися, що можна знайти нулі цієї функції, вирішивши рівняння $$f(x)=0$$

Якщо підставити$f(x) = ax^2 + bx + c$, то отримане рівняння $$a x^{2}+b x+c=0$$

називається квадратичним рівнянням. У попередньому розділі ми вирішували рівняння цього типу шляхом факторингу та використання властивості нульового добутку.

Однак не завжди можна розрахувати триноміал з лівого боку квадратного рівняння (1) як добуток множників з цілими коефіцієнтами. Для прикладу розглянемо квадратне рівняння $$2 x^{2}+7 x-3=0$$

Порівнюючи$2x^2 + 7x − 3$ з$ax^2 + bx + c$, давайте перерахуємо всі цілочисельні пари, добуток яких дорівнює ac = (2) (−3) = −6.

Жодна з цих цілих пар не додає до b = 7. Таким чином, квадратний триноміал$2x^2 + 7x − 3$ не врахує над цілими числами. Отже, нам знадобиться інший метод для розв'язання квадратного рівняння (2).

Метою цього розділу є розробка формули, яка послідовно надасть розв'язки загального квадратного рівняння (1). Однак, перш ніж ми зможемо розробити «Квадратичну формулу», нам потрібно закласти певну основу за участю квадратних коренів чисел.

Квадратні коріння

Ми починаємо наше обговорення квадратних коренів з дослідження розв'язків рівняння$x^2 = a$. Розглянемо досить просте рівняння.

$$x^{2}=25$$

Тому що$(−5)^2 = 25$ і$(5)^2 = 25$, рівняння (3) має два розв'язки, x = −5 або x = 5. Ми зазвичай позначаємо ці рішення одночасно, використовуючи знак «плюс або мінус»:

$$x=\pm 5$$

Ці розчини називаються квадратними корінцями з 25. Оскільки є два рішення, нам потрібні різні позначення для кожного. Позначимо позитивний квадратний корінь 25 з позначеннями$\sqrt{25}$ і негативний квадратний корінь 25 з позначеннями$-\sqrt{25}$. Таким чином,

$$\sqrt{25}=5 \qquad \text { and } \qquad-\sqrt{25}=-5$$

У подібному ключі рівняння$x^{2}=36$ має два рішення$x=\pm \sqrt{36}$, або альтернативно,$x=\pm 6$. Позначення$\sqrt{36}$ вимагає позитивного квадратного кореня, тоді як позначення$-\sqrt{36}$ вимагає негативного квадратного кореня. Тобто, $$\sqrt{36}=6 \qquad \text { and } \qquad-\sqrt{36}=-6$$

Не обов'язково, щоб права частина$x^2 = a$ рівняння була «ідеальним квадратом». Наприклад, рівняння

$$x^{2}=7 \quad \text { has solutions } \quad x=\pm \sqrt{7}$$

Немає раціонального квадратного кореня 7. Тобто немає можливості висловити квадратний корінь 7 у вигляді p/q, де p і q - цілі числа. Тому$\sqrt{7}$ є прикладом ірраціонального числа. Тим не менш,$\sqrt{7}$ це цілком дійсне дійсне число, і ми цілком комфортно залишаємо нашу відповідь у формі, показаній у рівнянні (4).

Однак, якщо для квадратного кореня 7 потрібно наближення, ми можемо міркувати, що оскільки 7 лежить між 4 і 9, квадратний корінь 7 буде лежати між 2 і 3. Оскільки 7 ближче до 9, ніж 4, розумним наближенням може бути

$$\sqrt{7} \approx 2.6$$

Калькулятор може забезпечити ще краще наближення. Наприклад, наші звіти TI83

$$\sqrt{7} \approx 2.645751311$$

Є два вироджені випадки, пов'язані з рівнянням$x^2 = a$, які вимагають нашої уваги.

1. Рівняння$x^{2}=0$ має тільки одне рішення, а саме х = 0. Таким чином,$\sqrt{0} = 0$.
2. Рівняння не$x^{2}=-4$ має дійсних розв'язків.4 Неможливо зробити квадрат дійсного числа і отримати −4. У цій ситуації ми просто констатуємо, що «рівняння не$x^{2}=-4$ має реальних розв'язків (немає розв'язків, які є дійсними числами)».

Приклад$\PageIndex{1}$

Знайти всі реальні розв'язки рівнянь$x^2 = 30, x^2 = 0, and x^2 = −14$.

Рішення

Рішення слідують.

• Рівняння$x^2 = 30$ має два реальних рішення, а саме$x=\pm \sqrt{30}$.
• Рівняння$x^2 = 0$ має одне дійсне рішення, а саме x = 0.
• Рівняння не$x^2 = -14$ має реальних розв'язків.

Спробуємо додаткові приклади.

Приклад$\PageIndex{2}$

Знайти всі реальні розв'язки рівняння$(x + 2)^2 = 43$.

Рішення

Є дві можливості для x + 2, а саме $$x+2=\pm \sqrt{43}$$

Щоб розв'язати для x, відніміть 2 з обох сторін цього останнього рівняння. $$x=-2 \pm \sqrt{43}$$

Хоча ця остання відповідь, як правило, є кращою формою відповіді, бувають випадки, коли потрібне наближення. Отже, наш TI83 дає наступні наближення.

$$-2-\sqrt{43} \approx-8.557438524 \qquad \text { and } \qquad-2+\sqrt{43} \approx 4.557438524$$

Приклад$\PageIndex{3}$

Знайти всі реальні розв'язки рівняння$(x − 4)^2 = −15$.

Рішення

Якщо x є дійсним числом, то так само є x − 4. Неможливо зробити квадрат дійсного числа x − 4 і отримати −15. Таким чином, дана проблема не має реальних рішень.

Розробка квадратичної формули

Тепер у нас є всі основи для розв'язання загального квадратного рівняння.

$$a x^{2}+b x+c=0$$

Ми будемо використовувати форму «завершення квадрата», щоб вирішити це рівняння для х. Давайте почнемо з віднімання c з обох сторін рівняння.

$$a x^{2}+b x=-c$$

Далі розділіть обидві сторони рівняння на a. $$x^{2}+\frac{b}{a} x=-\frac{c}{a}$$

Візьміть половину коефіцієнта х, як в (1/2) (b/a) = b/ (2a). Квадратуйте цей результат, щоб отримати$b^{2} /\left(4 a^{2}\right)$. Додайте цю суму до обох сторін рівняння.

$$x^{2}+\frac{b}{a} x+\frac{b^{2}}{4 a^{2}}=-\frac{c}{a}+\frac{b^{2}}{4 a^{2}}$$

Ліворуч ми фактуємо ідеальний квадратний триноміал. Справа отримуємо загальний знаменник і складаємо отримані еквівалентні дроби.

$$\begin{array}{l}{\left(x+\frac{b}{2 a}\right)^{2}=-\frac{4 a c}{4 a^{2}}+\frac{b^{2}}{4 a^{2}}} \\ {\left(x+\frac{b}{2 a}\right)^{2}=\frac{b^{2}-4 a c}{4 a^{2}}}\end{array}$$

За умови, що права частина цього останнього рівняння є позитивною, ми маємо два реальних розв'язки.

$$x+\frac{b}{2 a}=\pm \sqrt{\frac{b^{2}-4 a c}{4 a^{2}}}$$

Праворуч беремо квадратний корінь верхньої і нижньої частини дробу.

$$x+\frac{b}{2 a}=\pm \frac{\sqrt{b^{2}-4 a c}}{2 a}$$

Для завершення розв'язку нам потрібно лише відняти b/ (2a) з обох сторін рівняння.

$$x=-\frac{b}{2 a} \pm \frac{\sqrt{b^{2}-4 a c}}{2 a}$$

Хоча ця остання відповідь є цілком хорошим рішенням, ми зазвичай переписуємо рішення єдиним спільним знаменником.

$$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$$

Цей останній результат дає розв'язку загального квадратного рівняння (8). Розчин (9) називається квадратичною формулою.

Квадратична формула

Розв'язки квадратного рівняння $$a x^{2}+b x+c=0$$ задаються квадратичною формулою $$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$$

Хоча розробка квадратичної формули може залякати, на практиці її застосування досить просте. Давайте розглянемо кілька прикладів.

Приклад$\PageIndex{4}$

Використовуйте квадратичну формулу для вирішення рівняння $$x^{2}=27-6 x$$

Рішення

Першим кроком є розміщення рівняння у формі,$ax^2 + bx + c = 0$ перемістивши кожен член в одну сторону рівняння7, розташувавши члени у спадних ступенях x.

$$x^{2}+6 x-27=0$$

Далі$x^2 + 6x − 27 = 0$ порівняємо із загальним видом квадратного рівняння$ax^2 + bx + c = 0$ і відзначаємо, що a = 1, b = 6, а c = −27. Скопіюйте квадратичну формулу вниз.

$$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$$

Підставляємо a = 1, b = 6, а c = −27 і спрощуємо.

$$\begin{aligned} x &=\frac{-(6) \pm \sqrt{(6)^{2}-4(1)(-27)}}{2(1)} \\ x &=\frac{-6 \pm \sqrt{36+108}}{2} \\ x &=\frac{-6 \pm \sqrt{144}}{2} \end{aligned}$$

В даному випадку 144 - ідеальний квадрат. Тобто$\sqrt{144} = 12$, щоб ми могли продовжувати спрощувати $$x=\frac{-6 \pm 12}{2}$$

Важливо відзначити, що є дві реальні відповіді, а саме

$$x=\frac{-6-12}{2} \quad \text { or } \qquad x=\frac{-6+12}{2}$$

Спрощення, $$x=-9 \qquad \text { or } \qquad x=3$$

Цікаво відзначити, що цю проблему можна було б вирішити факторингом. Дійсно,

$$\begin{aligned} x^{2}+6 x-27 &=0 \\(x-3)(x+9) &=0 \end{aligned}$$

отже, властивість нульового добутку вимагає, щоб або x − 3 = 0 або x + 9 = 0, що призводить до x = 3 або x = −9, відповідей ідентичних тим, які знайдені квадратичною формулою.

Ми будемо мати більше сказати про «дискримінант» найближчим часом, але це не випадково, що квадратичний$x^2 + 6x − 27$ фактор. Ось відповідний факт.

Коли дискримінант - ідеальний квадрат

У квадратичній формулі $$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$$ число під радикалом$b^2 − 4ac$, називається дискримінантним. Коли дискримінант є ідеальним квадратом, квадратична функція завжди буде фактором.

Однак не завжди так, що ми можемо враховувати задану квадратику. Давайте розглянемо інший приклад.

Приклад$\PageIndex{5}$

За даними квадратичної функції$f(x) = x^2 − 2x$ знайти всі дійсні розв'язки f (x) = 2.

Рішення

$f(x) = x^2 − 2x$Тому що рівняння f (x) = 2 стає

$$x^{2}-2 x=2$$

Встановіть одну сторону рівняння, рівну нулю, віднімаючи 2 з обох сторін рівняння.

$$x^{2}-2 x-2=0$$

Порівняйте$x^2 − 2x − 2 = 0$ із загальним квадратним рівнянням$ax^2 + bx + c = 0$ і зверніть увагу, що a = 1, b = −2 і c = −2. Запишіть квадратичну формулу.

$$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$$

Далі підставляємо a = 1, b = −2, а c = −2. Зверніть увагу на обережне використання дужок.

$$x=\frac{-(-2) \pm \sqrt{(-2)^{2}-4(1)(-2)}}{2(1)}$$

Спростити. $$\begin{array}{l}{x=\frac{2 \pm \sqrt{4+8}}{2}} \\ {x=\frac{2 \pm \sqrt{12}}{2}}\end{array}$$

У цьому випадку 12 не є ідеальним квадратом, тому ми максимально спростили на даний час.10 Однак ми можемо наблизити ці рішення за допомогою калькулятора.

$$x=\frac{2-\sqrt{12}}{2} \approx-0.7320508076 \qquad x=\frac{2+\sqrt{12}}{2} \approx 2.732050808$$

Ми знайдемо ці наближення корисними в наступному.

Рівняння в прикладах$\PageIndex{4}$ і$\PageIndex{5}$ являють собою фундаментальний зрушення в нашій звичайній техніці розв'язання рівнянь. У минулому ми намагалися «ізолювати» терміни, що містять x (або щось невідоме, для якого ми розв'язуємо) на одній стороні рівняння, а всі інші члени на іншій стороні рівняння. Тепер, у Прикладах$\PageIndex{4}$ і$\PageIndex{5}$, ми виявляємо, що рухаємо все в одну сторону рівняння, роблячи одну сторону рівняння рівняння рівною нулю. Це несе деяке пояснення.

Лінійний або нелінійний

Припустимо, що невідоме, для якого ми розв'язуємо, є x.

• Якщо найвища потужність х, присутня в рівнянні, дорівнює x до першої степені, то рівняння лінійне. Так, наприклад, кожне з $$2 x+3=7, \quad 3-4 x=5 x+9, \quad \text { and } \qquad a x+b=c x+d$$ рівнянь лінійне.
• Якщо в рівнянні є степені x вище, ніж x до першого ступеня, то рівняння нелінійне. Так, наприклад, кожне з рівнянь $$x^{2}-4 x=9, \qquad x^{3}=2 x+3, \quad \text { and } \quad a x^{2}+b x=c x+d$$ нелінійне.

Стратегія вирішення рівняння буде зміщуватися в залежності від того, лінійне чи нелінійне рівняння.

Стратегія розв'язку — лінійна та нелінійна

При вирішенні рівнянь потрібно спочатку запитати, лінійне чи нелінійне рівняння. Знову ж таки, припустимо, що невідоме ми хочемо вирішити для є х.

• Якщо рівняння лінійне, перемістіть всі члени, що містять x, в одну сторону рівняння, всі інші члени - на іншу сторону рівняння.
• Якщо рівняння нелінійне, перемістіть всі члени в одну сторону рівняння, зробивши іншу сторону рівняння нулем.

Таким чином, оскільки ax + b = cx + d є лінійним у x, першим кроком у вирішенні рівняння було б переміщення всіх членів, що містять x, в одну сторону рівняння, всі інші терміни на іншу сторону рівняння, як у

$$a x-c x=d-b$$

З іншого боку, рівняння$ax^2 + bx = cx + d$ є нелінійним у x, тому першим кроком буде переміщення всіх членів в одну сторону рівняння, зробивши іншу сторону рівняння рівняння рівнянням рівняння рівнянням, як у $$a x^{2}+b x-c x-d=0$$

У$\PageIndex{5}$ прикладі$x^2−2x = 2$ рівняння нелінійне в х, тому ми перемістили все в ліву частину рівняння, зробивши праву частину рівняння рівняння рівним нулю, як в$x^2 −2x−2 = 0$. Однак не має значення, яку сторону ви робите рівним нулю. Припустимо, що ви переміщаєте кожен член в праву частину рівняння, як у $$0=-x^{2}+2 x+2$$

Порівнюючи$0 = −x^2 + 2x + 2$ із загальним квадратним рівнянням$0 = ax^2 + bx + c$, зверніть увагу, що a = −1, b = 2, а c = 2. Запишіть квадратичну формулу.

$$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$$

Далі підставляємо a = −1, b = 2, а c = 2. Знову ж таки, зверніть увагу на обережне використання дужок.

$$x=\frac{-(2) \pm \sqrt{(2)^{2}-4(-1)(2)}}{2(-1)}$$

Це призводить до двох рішень, $$x=\frac{-2 \pm \sqrt{4+8}}{-2}=\frac{-2 \pm \sqrt{12}}{-2}$$

У прикладі$\PageIndex{5}$ ми знайшли такі розв'язки та їх наближення.

$$x=\frac{2-\sqrt{12}}{2} \approx-0.7320508076 \qquad x=\frac{2+\sqrt{12}}{2} \approx 2.732050808$$

Це справедливе питання, щоб запитати, чи наші рішення$x=(-2 \pm \sqrt{12}) /(-2)$ однакові. Один із способів дізнатися це - знайти десяткові наближення кожного на нашому калькуляторі.

$$x=\frac{-2-\sqrt{12}}{-2} \approx 2.732050808 \qquad x=\frac{-2+\sqrt{12}}{-2} \approx-0.7320508076$$

Той факт, що ми отримуємо однакові десяткові наближення, повинен викликати впевненість у тому, що ми маємо однакові рішення. Однак ми також можемо маніпулювати точними формами наших рішень, щоб показати, що вони відповідають попереднім формам, знайденим у прикладі$\PageIndex{5}$.

Візьміть два розв'язки і помножте обидва чисельника і знаменника на мінус одиницю.

$$\frac{-2-\sqrt{12}}{-2}=\frac{2+\sqrt{12}}{2} \qquad \text { and } \quad \frac{-2+\sqrt{12}}{-2}=\frac{2-\sqrt{12}}{2}$$

Це показує, що наші рішення ідентичні тим, що знайдені в прикладі$\PageIndex{5}$.

Ми можемо зробити те ж заперечення чисельника і знаменника в компактній формі.

$$\frac{-2 \pm \sqrt{12}}{-2}=\frac{2 \mp \sqrt{12}}{2}$$

Зверніть увагу, що це призводить до однакових двох відповідей,$(2-\sqrt{12}) / 2$ і$(2+\sqrt{12}) / 2$.

З двох методів (перемістити всі терміни вліво або всі терміни вправо) ми віддаємо перевагу підходу Example$\PageIndex{5}$. Переміщаючи терміни в ліву частину рівняння, як і в$x^2 − 2x − 2 = 0$, коефіцієнт$x^2$ позитивний (a = 1) і ми уникаємо знака мінуса в знаменнику, виробленого квадратичною формулою.

Перехоплює

У прикладі$\PageIndex{5}$ ми використовували квадратичну формулу для пошуку розв'язків$x^2 − 2x − 2 = 0$. Ці розв'язки та їх наближення наведені в рівнянні (14). Важливо зробити зв'язок, що розв'язки в рівнянні (14) є нулями квадратичної функції$g(x) = x^2 − 2x − 2$. Нулі також забезпечують х-координати x-перехоплень графа g (параболи). Щоб підкреслити цей момент, давайте намалюємо графік параболи, що має рівняння$g(x) = x^2 − 2x − 2$.

Спочатку заповніть квадрат, щоб помістити квадратичну функцію у формі вершини. Візьміть половину середнього коефіцієнта та квадрат, як у$[(1/2)(−2)]^2 = 1$; потім додайте та відніміть цей термін, щоб рівняння залишалося збалансованим.

$$\begin{array}{l}{g(x)=x^{2}-2 x-2} \\ {g(x)=x^{2}-2 x+1-1-2}\end{array}$$

Фактор ідеальний квадратний триноміал, а потім об'єднати константи в кінці. $$g(x)=(x-1)^{2}-3$$

Це парабола, яка відкривається вгору. Вона зрушена вправо на 1 одиницю і вниз на 3 одиниці. Це дозволяє легко визначити вершину і намалювати вісь симетрії, як показано на малюнку$\PageIndex{1}$ (а).

Тепер буде очевидно, чому ми використовували наш калькулятор для наближення рішень в (14). Це x-координати x-перехоплювачів. Один x-перехоплення знаходиться приблизно за адресою (−0,73, 0), інший - приблизно (2,73, 0). Ці наближення використовуються для побудови розташування перехоплень, як показано на малюнку$\PageIndex{1}$ (b). Однак фактичними значеннями перехоплень є$((2-\sqrt{12}) / 2,0)$ і$((2+\sqrt{12}) / 2,0)$, і ці точні значення слід використовувати для анотування перехоплень, як показано на малюнку$\PageIndex{1}$ (b).

Нарешті, щоб знайти y-перехоплення, нехай x = 0 in$g(x) = x^2 − 2x − 2$. Таким чином, g (0) = −2, а y-перехоплення дорівнює (0, −2). Y-перехоплення та його дзеркальне відображення поперек осі симетрії побудовані на малюнку$\PageIndex{1}$ (c), де також показаний остаточний графік параболи.

Малюнок$\PageIndex{1}$

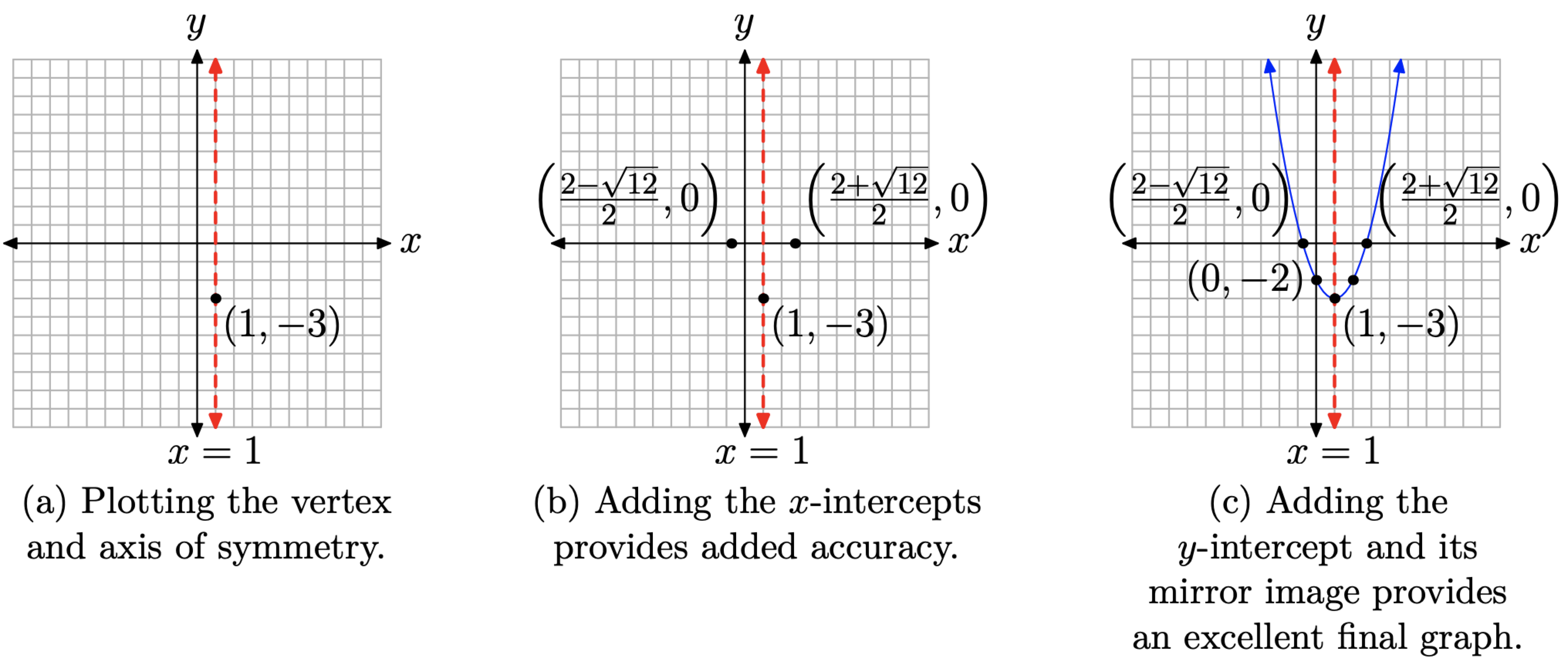
Ми зробили важливий момент і робимо паузу, щоб надати акцент.

Нулі та перехоплення

Всякий раз, коли ви використовуєте квадратну формулу для вирішення квадратного рівняння $$a x^{2}+b x+c=0$$

рішення $$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$$

нулі квадратичної функції $$f(x)=a x^{2}+b x+c$$

Розв'язки також забезпечують x-координати x-перехоплень графа f.

Потрібно обговорити одну остаточну концепцію.

Дискримінант

Розглянемо знову квадратне рівняння$ax^2 + bx + c = 0$ і розв'язки (нулі), надані квадратичною формулою

$$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$$

Вираз під радикалом$b^2 − 4ac$, називається дискримінантом, який ми позначимо буквою D. Тобто формула дискримінанта дається

$$D=b^{2}-4 a c$$

Дискримінант використовується для визначення характеру і кількості розв'язків квадратного рівняння$ax^2+bx+c = 0$. Робиться це без фактичного розрахунку рішень.

Давайте розглянемо три ключових приклади.

Приклад$\PageIndex{6}$

Розглянемо квадратне рівняння $$x^{2}-4 x-4=0$$ Обчисліть дискримінант і використовуйте його для визначення характеру і кількості розв'язків.

Рішення

Порівняйте$x^2 − 4x − 4 = 0$ з$ax^2 + bx + c = 0$ і зверніть увагу, що a = 1, b = −4, а c = −4. Дискримінант задається розрахунком

$$D=b^{2}-4 a c=(-4)^{2}-4(1)(-4)=32$$

Зауважте, що дискримінантний D є позитивним; тобто D > 0.

Розглянемо квадратичну функцію$f(x) = x^2 − 4x − 4$, яку можна записати у вигляді вершини

$$f(x)=(x-2)^{2}-8$$

Це парабола, яка відкривається вгору. Зсувається вправо на 2 одиниці, потім вниз на 8 одиниць. Тому він буде перетинати вісь x у двох місцях. Отже, можна було б очікувати, що квадратична формула забезпечить два реальних рішення (x-перехоплення). Дійсно,

$$x=\frac{-(-4) \pm \sqrt{(-4)^{2}-4(1)(-4)}}{2(1)}=\frac{4 \pm \sqrt{32}}{2}$$

Зверніть увагу, що дискримінант, D = 32, як обчислено вище, є числом під квадратним коренем. Ці розв'язки мають наближення

$$x=\frac{4-\sqrt{32}}{2} \approx-0.8284271247 \qquad \text { and } \qquad x=\frac{4+\sqrt{32}}{2} \approx 4.828427125$$

які допомагають у побудові точного графіка$f(x) = (x − 2)^2 − 8$, як показано на малюнку$\PageIndex{2}$.

Малюнок$\PageIndex{2}$. Якщо дискримінант позитивний, є два реальних x-перехоплення.

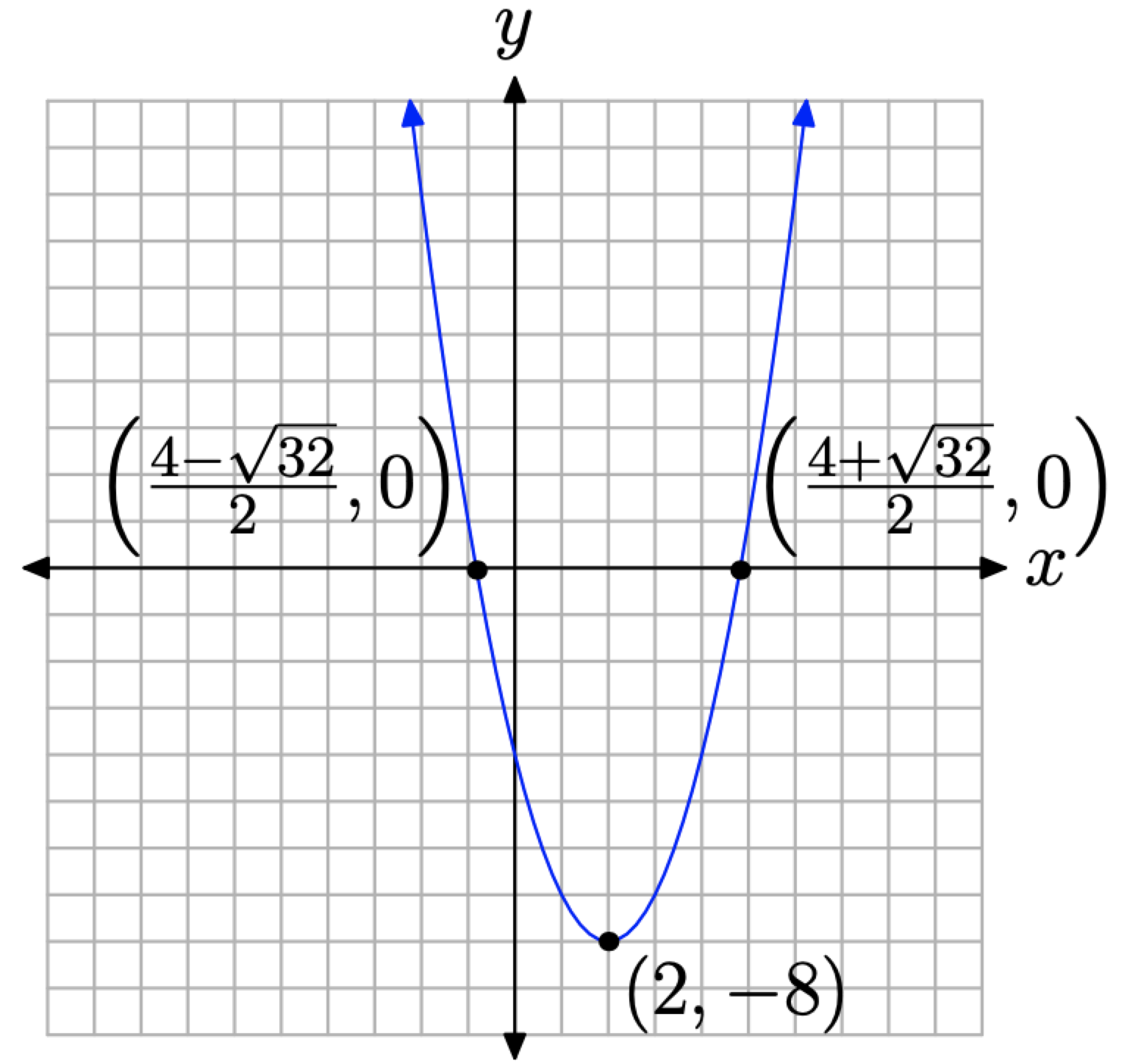
Таким чином, якщо дискримінант позитивний, парабола матиме два реальних x-перехоплення.

Далі розглянемо приклад, де дискримінант дорівнює нулю.

Приклад$\PageIndex{7}$

Розглянемо знову квадратне рівняння$ax^2 + bx + c = 0$ і розв'язки (нулі), надані квадратичною формулою

$$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$$ Вираз під радикалом$b^2 − 4ac$, називається дискримінантом, який ми позначимо буквою D. Тобто формула дискримінанта дається $$D=b^{2}-4 a c$$

Дискримінант використовується для визначення характеру і кількості розв'язків квадратного рівняння$ax^2+bx+c = 0$. Робиться це без фактичного розрахунку рішень. Розглянемо квадратне рівняння $$x^{2}-4 x+4=0$$

Обчисліть дискримінант і використовуйте його для визначення характеру і кількості розв'язків.

Рішення

Порівняйте$x^2 − 4x + 4 = 0$ з$ax^2 + bx + c = 0$ і зверніть увагу, що a = 1, b = −4, а c = 4. Дискримінант задається розрахунком

$$D=b^{2}-4 a c=(-4)^{2}-4(1)(4)=0$$

Зверніть увагу, що дискримінант дорівнює нулю.

Розглянемо квадратичну функцію$f(x) = x^2 − 4x + 4$, яку можна записати у вигляді вершини

$$f(x)=(x-2)^{2}$$

Це парабола, яка відкривається вгору і зміщується на 2 одиниці вправо. Зверніть увагу, що вертикального зсуву немає, тому вершина параболи буде спиратися на вісь x, як показано на малюнку$\PageIndex{3}$. В цьому випадку ми вважали за необхідне відкласти дві точки праворуч від осі симетрії, потім віддзеркалити їх поперек осі симетрії, щоб отримати точний сюжет параболи.

Малюнок$\PageIndex{3}$. Праворуч знаходиться таблиця балів, що задовольняють$f(x) = (x−2)^2$. Ці точки та їх дзеркальні зображення розглядаються як суцільні точки, накладені$f(x) = (x − 2)^2$ на графік зліва.

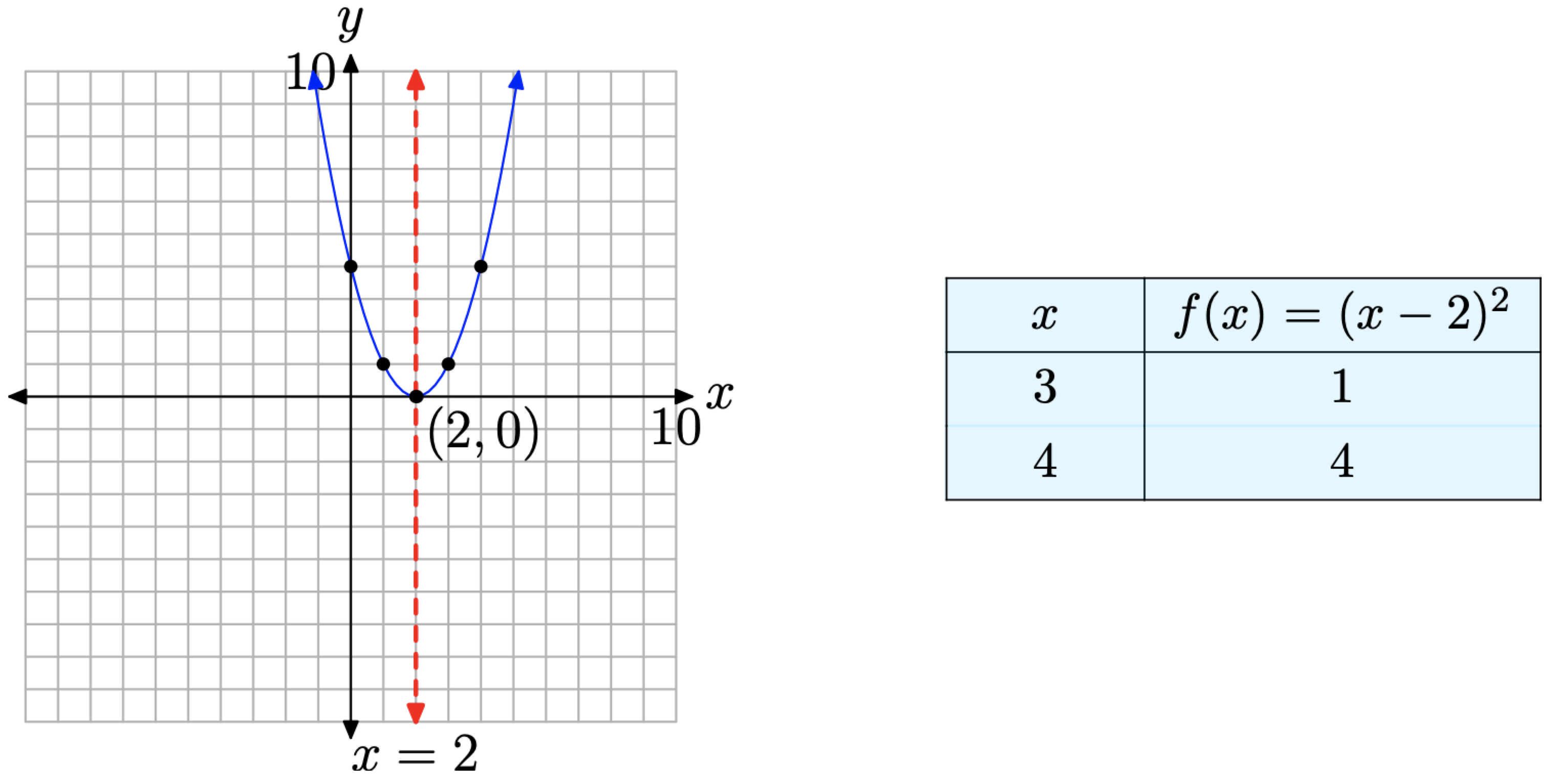
Придивіться до рівняння (17). Якщо встановити f (x) = 0 в цьому рівнянні, то отримаємо$0 = (x − 2)^2$. Це може бути записано 0 = (x − 2) (x − 2), і ми можемо сказати, що рішення є 2 і 2 знову. Однак математики вважають за краще говорити, що «2 - це рішення кратності 2» або «2 - подвійне рішення». 11 Зверніть увагу, як парабола дотична до осі х в місці розташування «подвійного рішення». Тобто парабола спускається з позитивної нескінченності, торкається (але не перетинає) вісь х при х = 2, потім знову піднімається до позитивної нескінченності. Звичайно, ситуація була б зворотна в параболі, відкритій вниз, як в$g(x) = −(x − 2)^2$, але графік все одно буде «цілувати» вісь x в місці розташування «подвійного рішення».

Тим не менш, ключовим моментом, який слід зазначити, є той факт, що дискримінантний D = 0 і парабола має лише один перехоплення x. Тобто рівняння$x^2 − 4x + 4 = 0$ має єдине дійсне рішення.

Далі розглянемо, що відбувається, коли дискримінант негативний.

Приклад$\PageIndex{8}$

Розглянемо квадратне рівняння $$x^{2}-4 x+8=0$$

Обчисліть дискримінант і використовуйте його для визначення характеру і кількості розв'язків.

Рішення

Порівняйте$x^2 − 4x + 8 = 0$ з$ax^2 + bx + c = 0$ і зверніть увагу, що a = 1, b = −4, а c = 8. Дискримінант задається розрахунком

$$D=b^{2}-4 a c=(-4)^{2}-4(1)(8)=-16$$

Зверніть увагу, що дискримінант негативний.

Розглянемо квадратичну функцію$f(x) = x^2 − 4x + 8$, яку можна записати у вигляді вершини

$$f(x)=(x-2)^{2}+4$$

Це парабола, яка відкривається вгору. Більш того, він повинен бути зміщений на 2 одиниці вправо і 4 одиниці вгору, так що не може бути х-перехоплень, як показано на малюнку$\PageIndex{4}$. Знову ж таки, ми вважали за необхідне в цьому прикладі намітити дві точки праворуч від осі симетрії, потім віддзеркалити їх, щоб отримати точний сюжет параболи.

Малюнок$\PageIndex{4}$. Праворуч знаходиться таблиця балів, що задовольняють$f(x)=(x-2)^{2}+4$. Ці точки та їх дзеркальні зображення розглядаються як суцільні точки, накладені$f(x)=(x-2)^{2}+4$ на графік зліва.

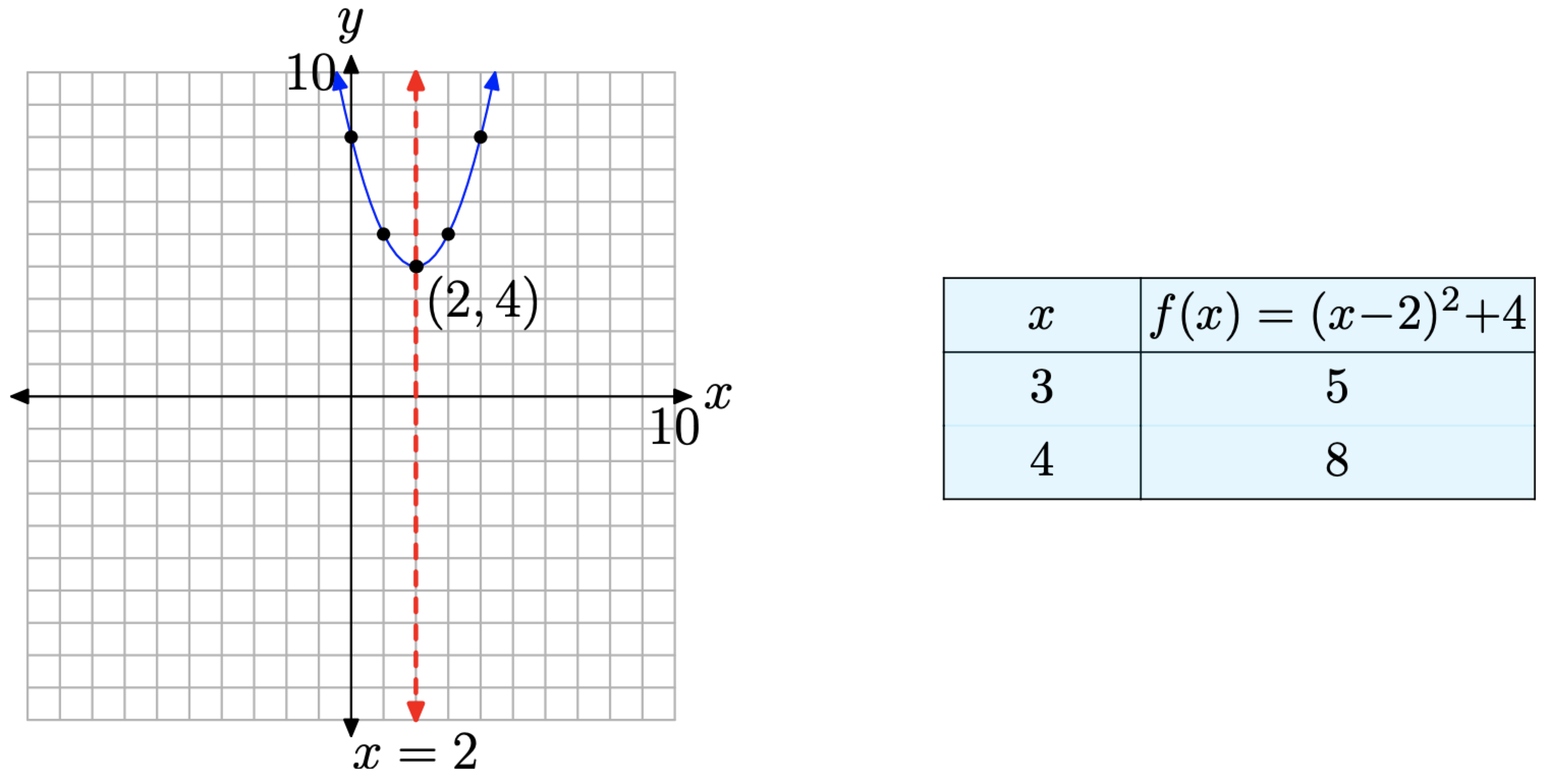
Ще раз ключовим моментом в даному прикладі є той факт, що дискримінант негативний і немає реальних розв'язків квадратного рівняння (еквівалентно, немає х-перехоплень). Давайте подивимося, що станеться, якщо ми насправді спробуємо знайти рішення$x^2 − 4x + 8 = 0$ використання квадратичної формули. Знову ж таки, a = 1, b = −4, а c = 8, тому $$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}=\frac{-(-4) \pm \sqrt{(-4)^{2}-4(1)(8)}}{2(1)}$$ спрощуючи, $$x=\frac{4 \pm \sqrt{-16}}{2}$$

Знову ж таки, пам'ятайте, що число під квадратним коренем є дискримінантом. У цьому випадку дискримінантом є −16. Неможливо зробити квадрат дійсного числа і отримати −16. Таким чином, квадратне рівняння не$x^2 − 4x + 8 = 0$ має реальних розв'язків, як передбачалося.

Давайте підсумуємо висновки в наших останніх трьох прикладах.

Резюме

Розглянемо квадратне рівняння $$a x^{2}+b x+c=0$$ . Дискримінант визначається як $$D=b^{2}-4 a c$$ .

Є три можливості:

1. Якщо D > 0, то квадратне рівняння має два дійсних розв'язку.
2. Якщо D = 0, то квадратне рівняння має одне дійсне рішення.
3. Якщо D < 0, то квадратне рівняння не має дійсних розв'язків.

Цей ключовий результат відбивається на графіку квадратичної функції.

Резюме

Розглянемо квадратичну функцію $$f(x)=a x^{2}+b x+c$$ .

Графік цієї функції є параболою. Три можливості існують залежно від значення дискримінанту$D = b^2 − 4ac$.

1. Якщо D > 0, парабола має два x-перехоплення.
2. Якщо D = 0, парабола має рівно один x-перехоплення.
3. Якщо D < 0, парабола не має x-перехоплень.

Вправа

У вправах 1 - 8 знайти всі реальні розв'язки заданого рівняння. Використовуйте калькулятор для наближення відповідей, поправте до найближчих сотих (два знака після коми).

Вправа$\PageIndex{1}$

$x^2 = 36$

Відповідь

$x = \pm 6$

Вправа$\PageIndex{2}$

$x^2 = 81$

Вправа$\PageIndex{3}$

$x^2 = 17$

Відповідь

$x = \pm \sqrt{17} \approx \pm 4.12$

Вправа$\PageIndex{4}$

$x^2 = 13$

Вправа$\PageIndex{5}$

$x^2 = 0$

Відповідь

х = 0

Вправа$\PageIndex{6}$

$x^2 = −18$

Вправа$\PageIndex{7}$

$x^2 = −12$

Відповідь

Немає реального рішення

Вправа$\PageIndex{8}$

$x^2 = 3$

У вправах 9 - 16 знайти всі реальні розв'язки даного рівняння. Скористайтеся калькулятором, щоб приблизити свої відповіді до найближчих сотих.

Вправа$\PageIndex{9}$

$(x−1)^2 = 25$

Відповідь

х = −4 або х = 6

Вправа$\PageIndex{10}$

$(x+3)^2 = 9$

Вправа$\PageIndex{11}$

$(x+2)^2 = 0$

Відповідь

х = −2

Вправа$\PageIndex{12}$

$(x−3)^2 = −9$

Вправа$\PageIndex{13}$

$(x+6)^2 = −81$

Відповідь

Немає реального рішення

Вправа$\PageIndex{14}$

$(x+7)^2 = 10$

Вправа$\PageIndex{15}$

$(x−8)^2 = 15$

Відповідь

$x = 8 \pm \sqrt{15} \approx 4.13, 11.87$

Вправа$\PageIndex{16}$

$(x+10)^2 = 37$

У Вправах 17 - 28 виконайте кожне з наступних завдань для заданої квадратичної функції.

1. Налаштуйте систему координат на аркуші графічного паперу. Позначте та масштабуйте кожну вісь. Не забудьте намалювати всі лінії лінійкою.
2. Помістіть квадратичну функцію у вигляді вершини. Покладіть вершину на вашій системі координат і позначте її координатами. Намалюйте вісь симетрії на вашій системі координат і позначте її рівнянням.
3. Використовуйте квадратичну формулу, щоб знайти х-перехоплення параболи. Використовуйте калькулятор для наближення кожного перехоплення, виправте до найближчого десятого, і використовуйте ці наближення для побудови x-перехоплень у вашій системі координат. Однак, позначити кожен x-перехоплення з його точними координатами.
4. Покладіть y-перехоплення на вашій системі координат та його дзеркальному відображенні по осі симетрії та позначте кожен своїми координатами.
5. Використовуючи всю інформацію у вашій системі координат, намалюйте графік параболи, а потім позначте його формою вершини функції. Використовуйте інтервальне позначення для визначення області та діапазону квадратичної функції.

Вправа$\PageIndex{17}$

$f(x) = x^2−4x−8$

Відповідь

Домен =$(−\infty, \infty)$,

Діапазон = [−12,$\infty$)

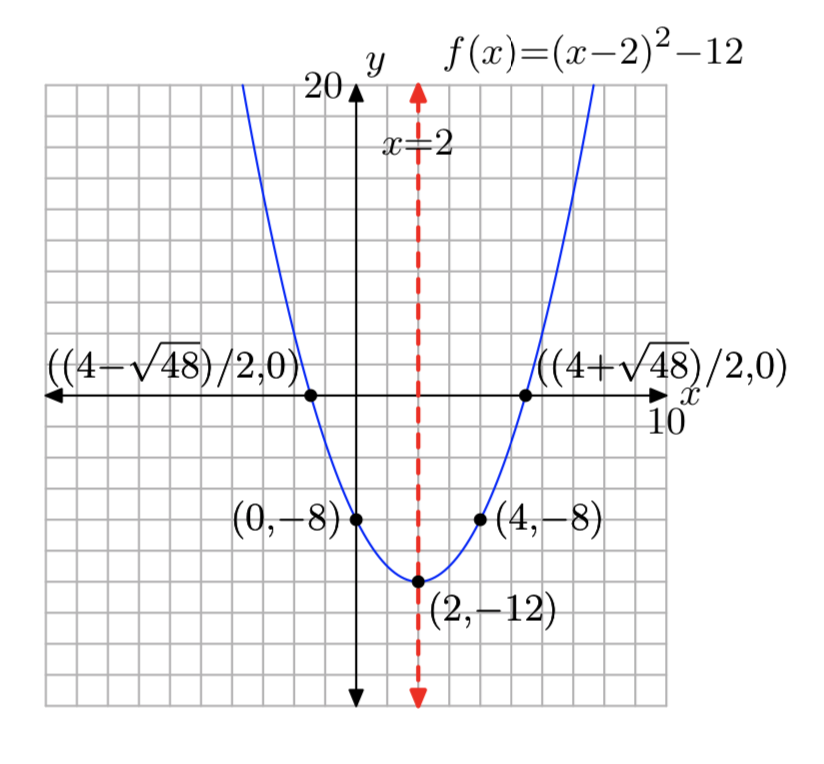
Вправа$\PageIndex{18}$

$f(x) = x^2+6x−1$

Вправа$\PageIndex{19}$

$f(x) = x^2+6x−3$

Відповідь

Домен =$(−\infty, \infty)$,

Діапазон = [−12,$\infty$)

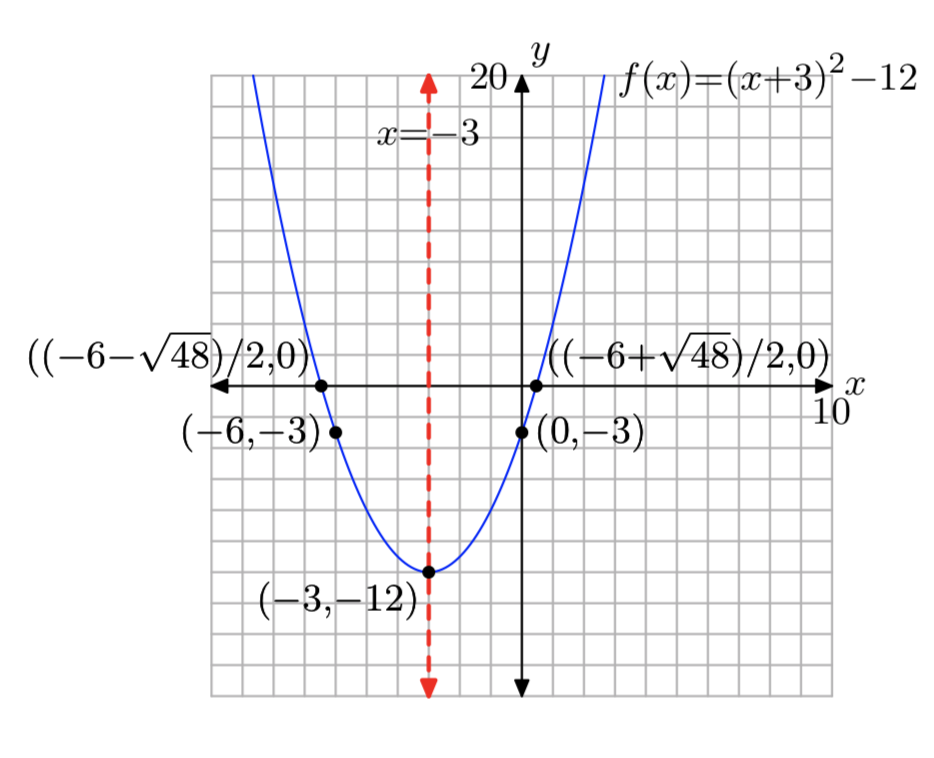
Вправа$\PageIndex{20}$

$f(x) = x^2−8x+1$

Вправа$\PageIndex{21}$

$f(x) = −x^2+2x+10$

Відповідь

Домен =$(−\infty, \infty)$,

Діапазон = (−$\infty$, 11]

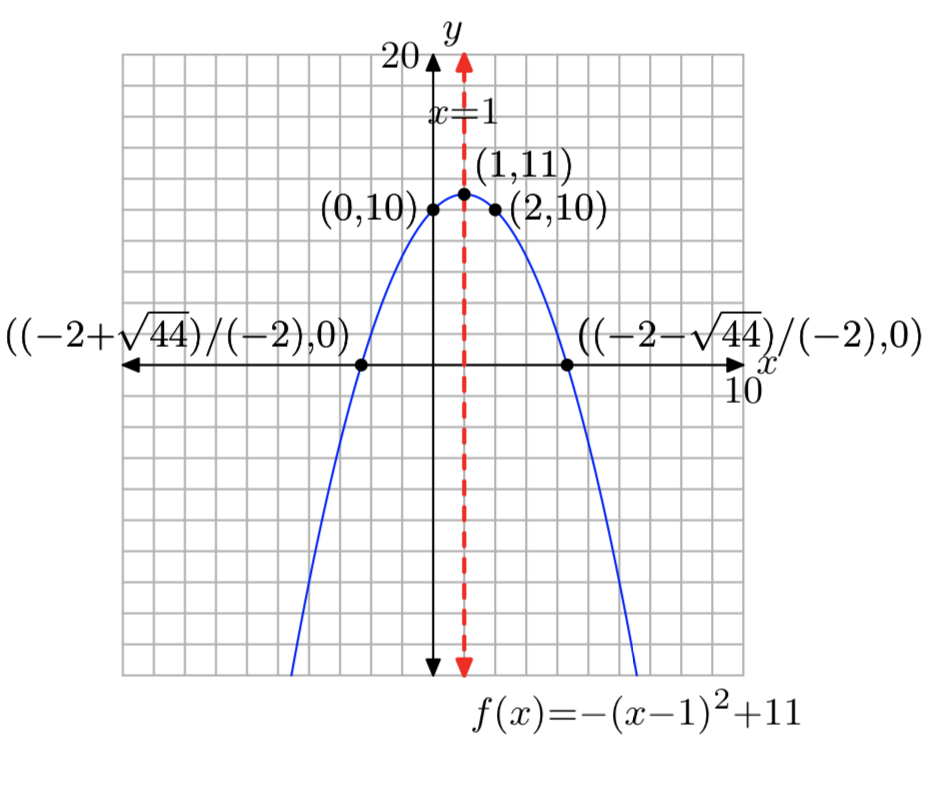
Вправа$\PageIndex{22}$

$f(x) = −x^2−8x−8$

Вправа$\PageIndex{23}$

$f(x) = −x^2−8x−9$

Відповідь

Домен =$(−\infty, \infty)$,

Діапазон = (−$\infty$, 7]

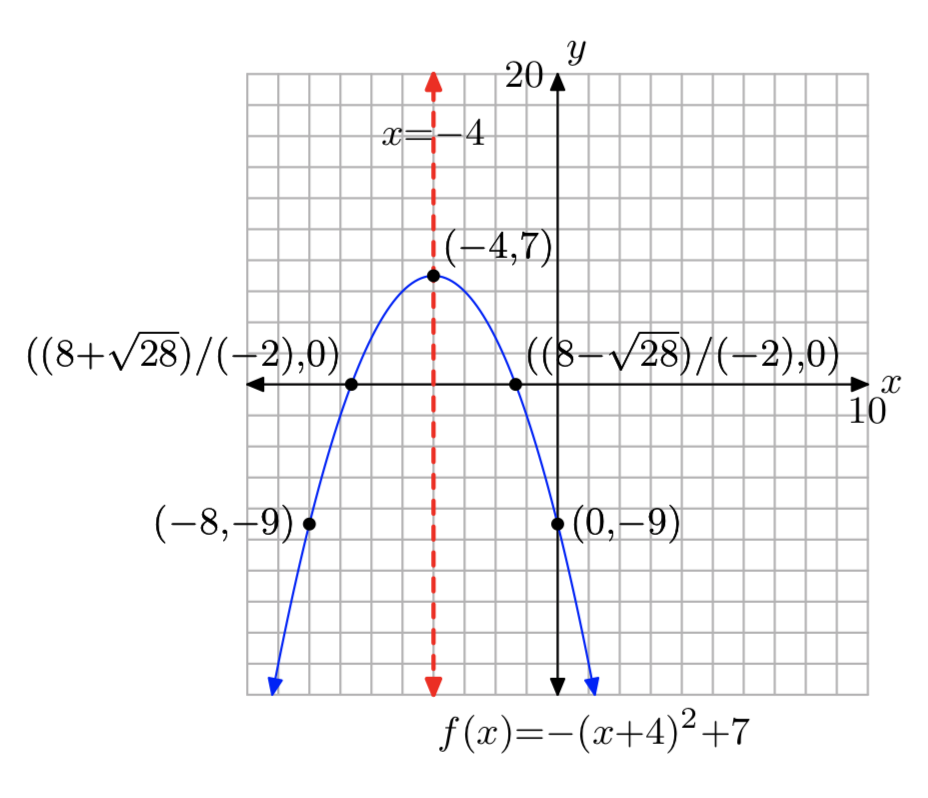
Вправа$\PageIndex{24}$

$f(x) = −x^2+10x−20$

Вправа$\PageIndex{25}$

$f(x)=2x^2−20x+40$

Відповідь

Домен =$(−\infty, \infty)$,

Діапазон = [−10,$\infty$)

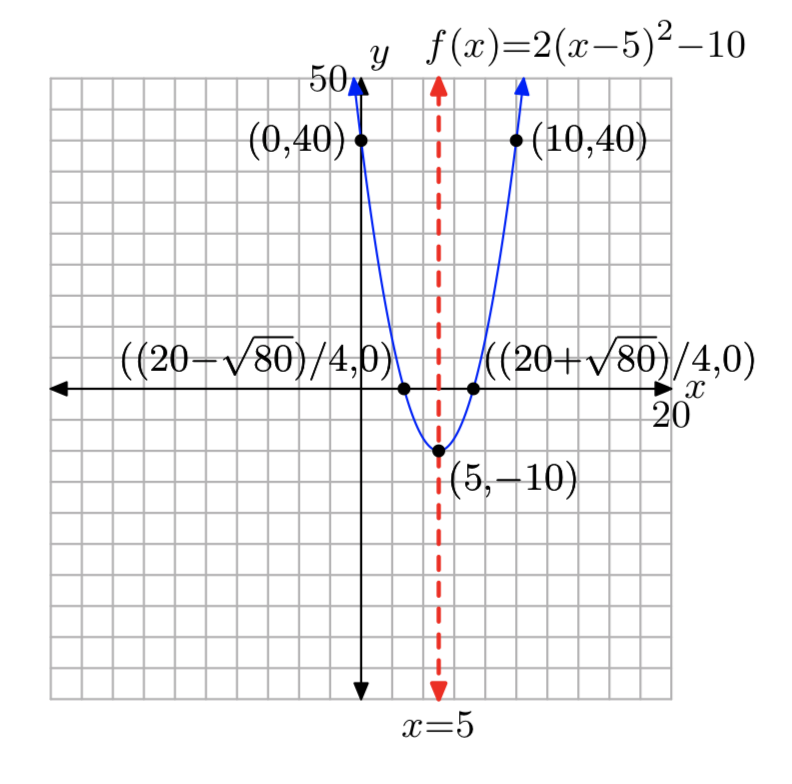
Вправа$\PageIndex{26}$

$f(x) = 2x^2−16x+12$

Вправа$\PageIndex{27}$

$f(x) = −2x^2+16x+8$

Відповідь

Домен =$(−\infty, \infty)$,

Діапазон = (−$\infty$, 40]

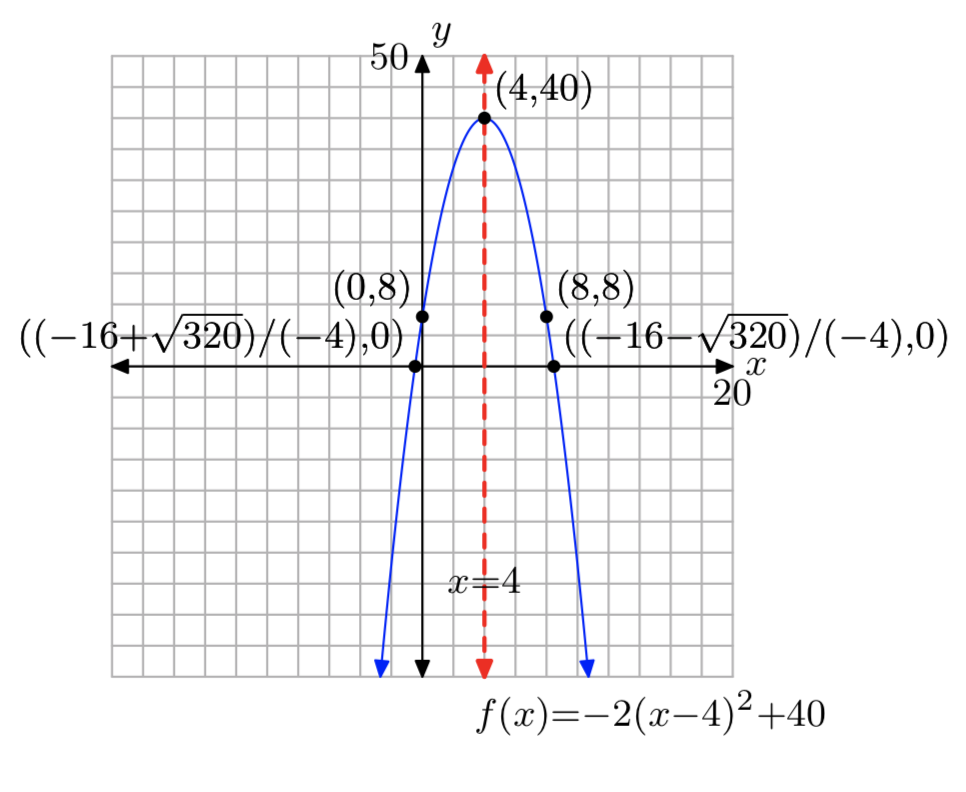
Вправа$\PageIndex{28}$

$f(x) = −2x^2−24x−52$

У вправах 29 - 32 виконайте кожне з наступних завдань для даного квадратного рівняння.

1. Налаштуйте систему координат на аркуші графічного паперу. Позначте та масштабуйте кожну вісь. Не забудьте намалювати всі лінії лінійкою.
2. Покажіть, що дискримінант негативний.
3. Використовуйте техніку завершення квадрата, щоб поставити квадратичну функцію у вигляді вершини. Покладіть вершину на вашій системі координат і позначте її координатами. Намалюйте вісь симетрії на вашій системі координат і позначте її рівнянням.
4. Покладіть y-перехоплення та його дзеркальне відображення поперек осі симетрії на вашій системі координат і позначте кожен з них своїми координатами.
5. Тому що дискримінант негативний (ви пам'ятаєте, щоб показати це?) , немає x-перехоплень. Використовуйте дане рівняння, щоб обчислити одну додаткову точку, потім побудуйте точку та її дзеркальне відображення поперек осі симетрії та позначте кожну своїми координатами.
6. Використовуючи всю інформацію у вашій системі координат, намалюйте графік параболи, а потім позначте його вершинною формою функції. Використовуйте інтервальне позначення для опису області та діапазону квадратичної функції.

Вправа$\PageIndex{29}$

$f(x) = x^2+4x+8$

Відповідь

Домен =$(−\infty, \infty)$,

Діапазон = [4,$\infty$)

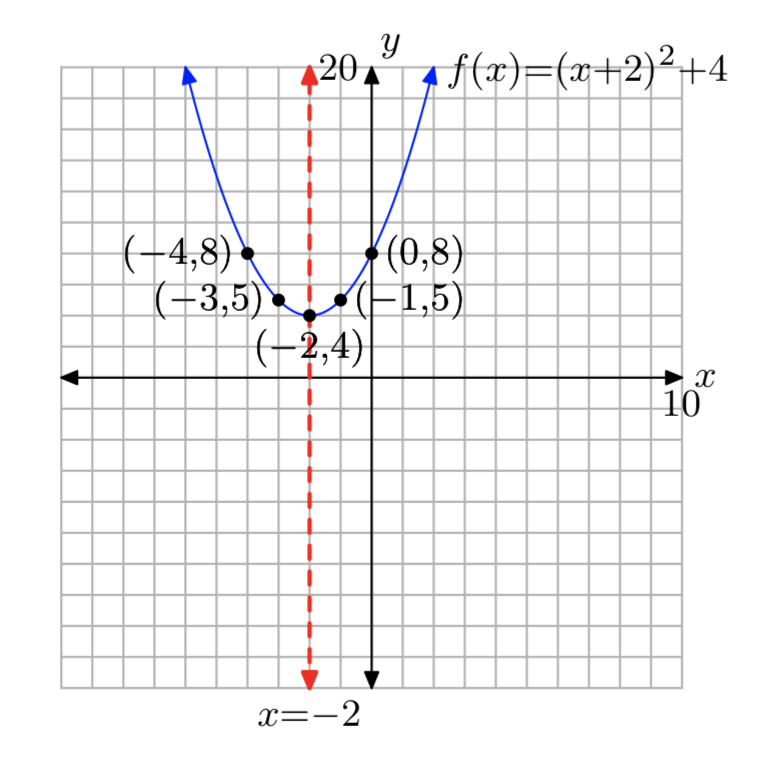
Вправа$\PageIndex{30}$

$f(x) = x^2−4x+9$

Вправа$\PageIndex{31}$

$f(x) = −x^2+6x−11$

Відповідь

Домен =$(−\infty, \infty)$,

Діапазон = (−$\infty$, −2]

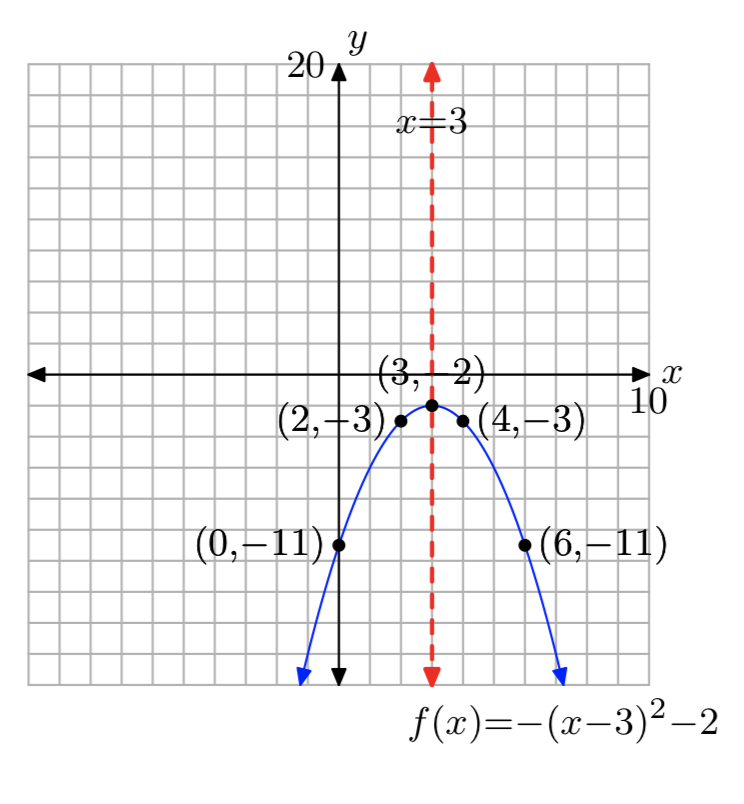
Вправа$\PageIndex{32}$

$f(x) = −x^2−8x−20$

У Вправах 33 - 36 виконайте кожне з наступних завдань для заданої квадратичної функції.

1. Налаштуйте систему координат на аркуші графічного паперу. Позначте та масштабуйте кожну вісь. Не забудьте намалювати всі лінії лінійкою.
2. Використовуйте дискримінант, щоб допомогти визначити значення k так, щоб графік заданої квадратичної функції мав рівно один x-перехоплення.
3. Підставте це значення k назад у задану квадратичну функцію, потім скористайтеся технікою завершення квадрата, щоб поставити квадратичну функцію у вигляді вершини. Покладіть вершину на вашій системі координат і позначте її координатами. Намалюйте вісь симетрії у вашій системі координат та позначте її рівнянням
4. Покладіть y-перехоплення та його дзеркальне відображення поперек осі симетрії та позначте кожен своїми координатами.
5. Використовуйте рівняння, щоб обчислити додаткову точку по обидві сторони від осі симетрії, потім побудуйте цю точку та її дзеркальне відображення поперек осі симетрії і позначте кожну з них своїми координатами.
6. Використовуючи всю інформацію у вашій системі координат, намалюйте графік параболи, а потім позначте його формою вершини функції. Використовуйте інтервальне позначення для опису області та діапазону квадратичної функції.

Вправа$\PageIndex{33}$

$f(x) = x^2−4x+4k$

Відповідь

к = 1

Домен =$(−\infty, \infty)$,

Діапазон = [0,$\infty$)

Вправа$\PageIndex{34}$

$f(x) = x^2+6x+3k$

Вправа$\PageIndex{35}$

$f(x) = kx^2−16x−32$

Відповідь

k = −2

Домен =$(−\infty, \infty)$,

Діапазон = (−$\infty$, 0]

Вправа$\PageIndex{36}$

$f(x) = kx^2−24x+48$

Вправа$\PageIndex{37}$

Знайти всі значення k так, щоб графік квадратичної функції$f(x) = kx^2−3x+5$ мав рівно два x-перехоплення.

Відповідь

{k:$k < \frac{9}{20}$}

Вправа$\PageIndex{38}$

Знайти всі значення k так, щоб графік квадратичної функції$f(x) = 2x^2+7x−4k$ мав рівно два x-перехоплення.

Вправа$\PageIndex{39}$

Знайти всі значення k так, щоб графік квадратичної функції не$f(x) = 2x^2−x+5k$ мав x-перехоплень.

Відповідь

{k:$k > \frac{1}{40}$}

Вправа$\PageIndex{40}$

Знайти всі значення k так, щоб графік квадратичної функції не$f(x) = kx^2−2x−4$ мав x-перехоплень.

У вправах 41 - 50 знайти всі реальні розв'язки, якщо такі є, рівняння f (x) = b.

Вправа$\PageIndex{41}$

$f(x) = 63x^2+74x−1$; б = 8

Відповідь

$−\frac{9}{7}, \frac{1}{9}$

Вправа$\PageIndex{42}$

$f(x) = 64x^2+128x+64$; б = 0

Вправа$\PageIndex{43}$

$f(x) = x^2−x−5$; б = 2

Відповідь

$\frac{1+\sqrt{29}}{2}, \frac{1−\sqrt{29}}{2}$

Вправа$\PageIndex{44}$

$f(x) = 5x^2−5x$; б = 3

Вправа$\PageIndex{45}$

$f(x) = 4x^2+4x−1$; б = −2

Відповідь

$−\frac{1}{2}$

Вправа$\PageIndex{46}$

$f(x) = 2x^2−9x−3$; b = −1

Вправа$\PageIndex{47}$

$f(x) = 2x^2+4x+6$; б = 0

Відповідь

немає реальних рішень

Вправа$\PageIndex{48}$

$f(x) = 24x^2−54x+27$; б = 0

Вправа$\PageIndex{49}$

$f(x) = −3x^2+2x−13$; б = −5

Відповідь

немає реальних рішень

Вправа$\PageIndex{50}$

$f(x) = x^2−5x−7$; б = 0

У вправах 51 - 60 знайти всі реальні розв'язки квадратного рівняння, якщо такі є.

Вправа$\PageIndex{51}$

$−2x^2+7 = −3x$

Відповідь

$\frac{3−\sqrt{65}}{4}, \frac{3+\sqrt{65}}{4}$

Вправа$\PageIndex{52}$

$−x^2 = −9x+7$

Вправа$\PageIndex{53}$

$x^2−2 = −3x$

Відповідь

$−\frac{3−\sqrt{17}}{2}, −\frac{3+\sqrt{17}}{2}$

Вправа$\PageIndex{54}$

$81x^2 = −162x−81$

Вправа$\PageIndex{55}$

$9x^2+81 = −54x$

Відповідь

− 3

Вправа$\PageIndex{56}$

$−30x^2−28 = −62x$

Вправа$\PageIndex{57}$

$−x^2+6 = 7x$

Відповідь

$−\frac{7+\sqrt{73}}{2}, −\frac{7−\sqrt{73}}{2}$

Вправа$\PageIndex{58}$

$−8x^2 = 4x+2$

Вправа$\PageIndex{59}$

$4x^2+3 = −x$

Відповідь

немає реальних рішень

Вправа$\PageIndex{60}$

$27x^2 = −66x+16$

У Вправи 61 - 66 знайдіть всі перехоплення x, якщо такі є, заданої функції.

Вправа$\PageIndex{61}$

$f(x) = −4x^2−4x−5$

Відповідь

немає x-перехоплює

Вправа$\PageIndex{62}$

$f(x) = 49x^2−28x+4$

Вправа$\PageIndex{63}$

$f(x) = −56x^2+47x+18$

Відповідь

($\frac{9}{8}$, 0), ($−\frac{2}{7}$, 0)

Вправа$\PageIndex{64}$

$f(x) = 24x^2+34x+12$

Вправа$\PageIndex{65}$

$f(x) = 36x^2+96x+64$

Відповідь

($−\frac{4}{3}$, 0)

Вправа$\PageIndex{66}$

$f(x) = 5x^2+2x+3$

У вправах 67 - 74 визначте кількість дійсних розв'язків рівняння.

Вправа$\PageIndex{67}$

$9x^2+6x+1 = 0$

Відповідь

1

Вправа$\PageIndex{68}$

$7x^2−12x+7 = 0$

Вправа$\PageIndex{69}$

$−6x^2+4x−7 = 0$

Відповідь

0

Вправа$\PageIndex{70}$

$−8x^2+11x−4 = 0$

Вправа$\PageIndex{71}$

$−5x^2−10x−5 = 0$

Відповідь

1

Вправа$\PageIndex{72}$

$6x^2+11x+2 = 0$

Вправа$\PageIndex{73}$

$−7x^2−4x+5 = 0$

Відповідь

2

Вправа$\PageIndex{74}$

$6x^2+10x+4 = 0$

​​​​​​​